感应线圈车辆检测器数据的预处理方法研究

陶汉卿

(柳州铁道职业技术学院电子工程系，广西 柳州 545616)

感应线圈车辆检测器数据的预处理方法研究

陶汉卿

(柳州铁道职业技术学院电子工程系，广西 柳州 545616)

为提高感应线圈车辆检测器的感应曲线特征提取和交通信息检测的准确率，文章以感应线圈车辆检测器的感应曲线信号为基础，研究了感应线圈信号曲线的预处理方法，并通过基于中值滤波和聚类分析的基频漂移抑制实验验证，表明该预处理方法能很好地抑制噪声，达到了较为理想的效果，具有极大的应用前景和推广价值。

车辆检测器；中值滤波；聚类分析；数据预处理

0 引言

随着经济和社会的高速发展，交通问题越来越突出，智能交通系统(ITS)运用计算机技术、网络技术、自动控制技术解决交通问题，提高交通的运输能力和效率，要实现智能交通系统的管理和控制，交通信息获取是基础，是智能交通系统中的关键部分。应用于交通信息采集的设备很多，如感应线圈、视频监控、红外线、激光信息采集，感应线圈于同类设备比较，具有稳定和可靠性好、性价比和检测精度高、使用时间长和技术成熟等优势。本文以感应线圈车辆检测器采集到的数据为基础，对感应曲线数据预处理算法进行了研究。

目前感应线圈交通信息采集的技术已经相当成熟，但利用其采集的数据进行处理分析的研究还很有限，提升空间较大，因此近年来吸引了不少研究者的关注。而现有的基于感应线圈的感应数据曲线的预处理技术还很少，基线漂移抑制具有不同的解决方案，如基于FIR和IIR滤波器的基线漂移抑制法、基于自适应滤波器的基线漂移抑制方法、运用小波分解方法抑制基线漂移，但是这些方法具有不同的缺陷：基于FIR和IIR滤波器的基线漂移抑制法，不适用于噪声频率超过截止频率的情况[1]；基于自适应滤波器的基线漂移抑制方法需要参考一段时间内采集到的噪声信号，而该信号与所需要采集的信号没有关联[2]；小波分解方法需要对基线移频信号进行分解，然后再滤波，对于和噪声信号接近时的采集信号，该方法无法准确滤波。在平滑滤波方面，文献[4]提出了“五点三次”的方法对感应线圈曲线数据进行平滑滤波，平滑后的曲线很好地揭示了信号的主要起伏特征(突出波峰、波谷)，但是还可以进一步改进。因此，有必要对感应数据曲线的预处理技术进行深入的研究。

1 感应线圈数据曲线感应数据预处理需求分析

本文以感应线圈车辆检测器的感应曲线信号为基础，对感应线圈数据处理分析技术进行深入研究。各种车辆经过感应线圈时产生的典型信号曲线如图1所示，其中横坐标为时间，纵坐标为频率变化值[4]，感应线圈数据是离散的时间序列，具有随机性。

大客车小客车大货车中货车小货车拖挂车摩托车自行车

图1 常用车识别典型曲线图

由数据采集系统获取的感应数据是最原始的，其蕴含了各种不同成因下的干扰信号，包括长期工作后感应线圈的老化变形，温度、电磁场等环境因素的影响，倘若直接利用这些数据进行实时交通信息处理和分析，必然导致较差的效果，严重影响交通信息检测的精度和结果的可靠性。因此，在实时交通信息处理和分析步骤之前，必须对原始数据进行一系列的预处理，剔除不同干扰因素的噪声信号，提取原始数据的真实信息。感应线圈曲线数据预处理的流程如图2所示。

图2 感应数据预处理流程图

(1)感应线圈车辆检测器采集原始数据，对噪声和信号进行压缩处理；

(2)采用聚类分析融合分离和剔除出无效信号，用中值滤波的方法获取准确的车辆检测器感应数据；

(3)采用chebyshev多项式拟合的方法进行平滑滤波处理，得到感应曲线的准确特征。

2 感应线圈车辆检测器数据的预处理方法

2.1 中值滤波的算法

传统中值滤波的算法[5]是：建立一个长度为N=2L+1(L=1，2，…，n)，N为奇数，组成滤波窗口，移动离散信号序列窗口中心，采用升序或降序的方式排列每个窗口的数据；把原中心位置的值更换为排序所得的中值，该算法窗口数据排序频繁，速度慢，实时性低。

2.2 基于中值滤波和聚类分析的基频漂移抑制方法

本文在传统中值滤波算法的基础上进行改进，对车辆检测器的基频漂移进行抑制：利用一个长度为N的时间窗沿着时间轴作聚类分析，把窗内的N个原始数据序列x(n)，…，x(n+N-1)分成基频信号和“异常信号”两个簇(通常基频类的聚类中心值较小，而“异常信号”类的聚类中心值较大)，以基频信号序列中第K个位置为中心，取2L+1个数据，建立一个滚动窗口，设窗口数据为：W[i](i=0，1…，2L+1)，将窗口的前2L+1个数据进行降序排序放到数组F[i](i=0，1…L)，则中值为F1[L]，更新基频值为中值点，向横坐标时间轴移动窗口，然后插入前一个窗口数据的中值F1[L]作为新数据，为保持窗口的长度2L+1不变，需要剔除原窗口中最左端的数据，然后重复上述的步骤，对新窗口进行聚类分析，新窗口为2L+1个数据序列x(n+1)，…(x+N)，根据以下公式(1)～(4)对窗口的后2L+1数据进行比较判断[6]，F2[L]为窗口后2L+1个数据的中值，作为该窗口的新基频值，通过窗口和中值的滚动计算，选取，可以跟踪基频，从而实现基频漂移抑制。

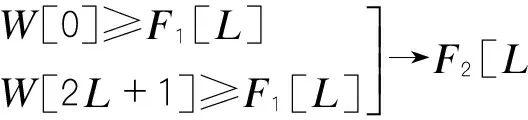
(1)

(2)

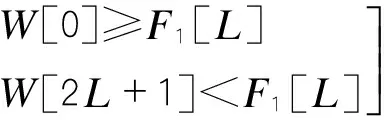
(3)

(4)

正确地选取滤波窗口的大小N直接影响基频漂移跟踪的效果[7]。N值太小，会影响聚类的准确性，算法失去了基频漂移抑制的效果；N值过大，滤波窗口过大，会导致时间间距太大，计算的基频聚类中心值与当前值具有一定的差距，基频漂移无法进行跟踪。根据实验计算，N一般取7～11(L一般取3～5)。

2.3Chebyshev多项式

Tn(x)=cos(narccosx)

(5)

该式被称为切比雪夫(Chebyshev)多项式。

切比雪夫多项式具有以下性质[8]：

(1)正交性

(6)

(2)递推关系

Tn+1(x)=2xTn-Tn-1(x)，n≥1

(7)

由T0(x)=1，T1(x)=x递推可得：

T2(x)=2x2-1

T3(x)=4x3-3x

T4(x)=8x4-8x2+1

T5(x)=16x5-20x3+5x

T6(x)=32x6-48x4+18x2+1

(8)

显然，Tn(x)的首项系数an=2n-1(n≥1)。

(3)奇偶性

当n为奇数时，Tn(x)为奇函数；当n为偶数时，Tn(x)为偶函数。即Ln(-x)=(-1)nLn(x)。

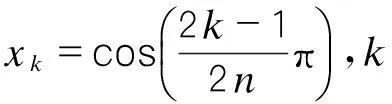
2.4 感应数据的Chebyshev多项式拟合

应用Chebyshev多项式拟合感应数据的步骤如下：

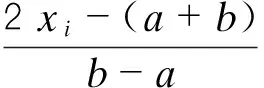
(9)

(2)根据性质2中的式(8)，计算

T0(ti)=1，T1(ti)=ti，i=1，…，m，

(10)

以及

T2(ti)，…，Tn(ti)，i=1，…，m；

(11)

(3)计算内积

(12)

(13)

(4)求法方程组

[(Tj，Tk)]c=b

(14)

的解c=[c0，c1，…，cn]T，其中b=[(y，T0)，(y，T1)，…(y，Tn)]T；

(5)由区间变换

(15)

计算得到t值后，相应计算Tk(t)的值(k=0，1，…，n)。

(6)感应数据的多项式拟合为

f(x)=c0T0(t)+c1T1(t)+…+cnTn(t)。

(16)

在感应数据时间序列个数>m+1(m>0)的情况下，都能够拟合到一个n阶Chebyshev多项式，该Chebyshev多项式拟合方法要求m远大于n，这对于感应线圈数据信号序列是普遍适合的。拟合的阶数越高，拟合点越准确，由于高阶次会增加计算量，数据点吻合好不代表拟合合理，但是并非拟合的阶次越高越好[9]。实验证明阶数≤6效果最好，所以本文阶数取n=5。

3 实验分析

基于中值滤波和聚类分析的基频漂移抑制实验如图3所示。

(a)基于中值滤波和聚类分析的基频漂移跟踪曲线

(b)基频漂移抑制后的车辆感应曲线

从图3(b)可以看出，感应信号较强的车辆(如小轿车)，其频率数据(单位为HZ)变化峰值>600，而感应信号较弱的车辆(如自行车)，其频率数据变化峰值很小，一般在30左右，同时也可以从图3(a)中看出，基频漂移是缓慢变化的，但是变化的幅度在一定时间内超过了感应信号较弱的车辆的幅值。因此需要对基频漂移进行跟踪和抑制。

采集到的原始信号序列为X1=[3 46 103 188 201 193 182 190 192 171 53 22 18 8 29 48 100 170 173 176 166 167 173 185 178 68 36 17 8]；

经过中值滤波和聚类分析的基频漂移进行基频漂移后为X2=[3 46 98 189 201 183 185 190 192 150 55 22 18 8 20 50 102 170 173 168 171 167 170 175 178 70 33 17 8]；

根据理论计算值为X3=[3 46 98 188 201 183 182 190 192 150 53 22 18 8 20 48 100 170 173 168 166 167 173 175 178 68 33 17 8]；

利用公式S=max{Xi，j[k]-X3[k]}(i，j=1，2，k=1，2，3…)计算最大误差。采集到的原始信号最大误差为：X1[10]-X3[10]=171-150=21；中值滤波和聚类分析的基频漂移抑制后最大误差为：X2[21]-X3[21]=171-166=5。

实验结果表明：中值滤波和聚类分析的基频漂移抑制后最大误差仅为5，比采集到的原始信号最大误差小很多，提高了采集的感应线圈车辆传感器数据的准确性，因此基于中值滤波和聚类分析的基频漂移抑制方法，能自动区分车辆感应数据和基频漂移数据的能力，并且可以利用基频信号聚类中心实时更新当前基频值。故能有效抑制基频漂移，并且成功分离车辆感应信号，达到较理想的效果。

经过抑制基线漂移后，对采集到的感应线圈数据信号，进行Chebyshev多项式拟合平滑滤波，结果如图4所示。实验结果表明：平滑滤波后能更为准确地反映感应曲线的特征，所以该方法是有效的。

图4 感应曲线平滑滤波图

4 结语

本文阐述的感应线圈数据的预处理方法能很好地抑制基频漂移，平滑滤波后的数据曲线进一步揭示了信号的主要起伏特征(突出波峰、波谷)，这对于提高感应线圈车辆检测器的抗干扰能力具有重要的意义，平滑滤波使得曲线的特征提取更加准确，从而提高了车流量、车速、车型等交通信息的检测精度。

[1]邹 波，周 远.一种滤除基线漂移和工频干扰的数字滤波算法[J].深圳职业技术学院学报，2005(4)：3-5.

[2]李 刚，刘 巍，虞启琏，等.抑制工频干扰及基线漂移的快速算法[J].中国生物医学工程学报，2000，19(1)：63-65.

[3]李小燕，王 涛，冯焕清，等.基于小波变换的自适应滤波器消除ECG中基线漂移[J].中国科学技术大学学报.2000，30(4)：450-454.

[4]林培群.道路交通参数及交通事件智能检测关键技术研究[D].广州：华南理工大学，2008.

[5]林成森.数值计算方法[M].北京：科学出版社，2005.

[6]危疆树.中值滤波算法及其并行化研究[J].福建电脑，2008(7)：101-101.

[7]YINL，YANGR，GABBOUJM，NEUVOY.Weightedmedianfilters：atutorial[J].IEEETransCircuitsSystem，1996，43(3)：157-192.

[8]张可村，赵英良.数值计算的算法与分析[M].北京：科学出版社，2002.

[9]徐宜会，赵宝贵.Matlab在数据拟合中的应用[J].科技广场，2007，34(2)：169-170.

Study on the Preprocessing Methods of Induction Coil Vehicle Detector Data

TAO Han-qing

(Department of Electronic Engineering，Liuzhou Railway Vocational and Technical College，Liuzhou，Guangxi，545616)

To improve the accuracy of induction curve feature extraction and traffic information detection for the induction coil vehicle detector，based on induction curve signal of induction coil vehicle detector，this article studied the preprocessing methods of induction coil signal curve，and through the base fre-quency drift suppression experiments based on median filtering and cluster analysis，it showed that this preprocessing method can suppress the noise，reaching more satisfactory results，thus it has great ap-plication prospects and promotional value.

Vehicle detector；Median filtering；Cluster analysis；Data preprocessing

陶汉卿，硕士，讲师，从事智能交通系统方面的教学科研工作。

2013年度广西高校科学技术研究项目“城市轨道交通车载测速定位装置的研制”(编号：2013YB358)

U

A

10.13282/j.cnki.wccst.2015.07.015

1673-4874(2015)07-0063-05

2015-06-06