粉末冶金皮带轮模压致密化成型的数值模拟

(西华大学材料科学与工程学院，四川 成都 610039)

·先进材料及能源·

粉末冶金皮带轮模压致密化成型的数值模拟

郭 彪, 魏晓伟，敖进清，肖贤通

(西华大学材料科学与工程学院，四川 成都 610039)

编写Fortran程序将粉体材料本构模型写入有限元分析系统，模拟铁粉压缩致密化过程，将预测的载荷位移曲线与实测结果对比，验证粉体材料本构模型的有效性。基于验证的本构模型，模拟分析粉末冶金皮带轮的模压致密化成型过程，预测压坯各部位的相对密度分布。通过补偿压坯低密度区的装粉量，有效提高和改善了压坯的密度和密度分布。实践表明优化后的压制工艺可压制出合格的粉末冶金皮带轮压坯，为此类粉末冶金零件的模压成型设计提供参考。

粉末冶金；皮带轮；密度分布；数值模拟

粉末冶金技术具有低成本、近净成形等显著优点而广泛用于生产发动机传动件、通用机械零件和工具等，特别是汽车工业已成为粉末冶金零件的最大应用市场，对粉末冶金零件的力学性能和尺寸精度也提出了越来越高的要求[1-2]。密度和密度分布是影响粉末冶金零件性能和尺寸的关键因素，通常粉末冶金零件密度越高，其物理和力学性能也随之大幅提高[3]；然而，实际压制过程中，零件各部位粉末压缩、移动不同，加上模具表面对粉末摩擦的影响，导致零件压坯密度分布不均匀，降低零件尺寸精度，引起零件烧结和热处理变形，甚至开裂。同时，不均匀的密度分布也往往导致零件在最低密度处发生破坏，影响整个零件的性能和使用寿命。因此，为了充分利用粉末冶金材料的性能，在设计零件压制模具和工艺时应尽量减小压坯各部位的密度差。

塑性成形有限元数值模拟技术能有效地模拟和分析粉体材料的压缩致密化过程，指导粉末冶金零件的压制工艺和模具设计，取代经验性的试错法，减少设计周期，降低生产成本。

目前，粉体致密化成形数值模拟中常用的方法有金属塑性力学法、广义塑性力学(土塑性力学)法和微观力学(离散单元)法等，其中前2种方法实用性更好，微观力学法因难以考虑与实际零件生产等同数量的粉末颗粒数，尚未应用于实际生产[4]。

欧阳鸿武等[5]、王德广等[6]分别基于金属塑性力学法模拟了装粉和压制方式对粉体模压成形过程的影响，探讨了粉体材料的致密化成形机制。Li等[7]基于金属塑性力学法模拟铁粉的温压致密化成形，表明相同条件下压制温度高时所需的成形载荷低，摩擦是影响压坯密度和分布的主要因素。Kim等[8]基于金属塑性力学法模拟了粉末与芯棒间不同摩擦因素对铁粉冷等静压致密化过程的影响，发现低摩擦因素时压坯密度分布更均匀。李元元等[4]基于金属塑性力学法归纳了粉体模压致密化成形本构模型的通式。随后，Song等[9]通过实验和数值模拟对比研究，发现不同模型对粉体致密化成形过程的预测差异较大，并在此基础上建立了实验用铁粉材料的屈服模型，嵌入有限元软件模拟和指导粉末冶金零件的模压过程。Lee等[10]基于广义塑性力学法模拟铝合金粉体的压制过程，预测了压坯成形压力和密度分布。Zhou等[11]基于广义塑性力学法模拟了粉末压坯成形过程中的压制、脱模力，研究了相对密度和残余应力分布。目前，针对复杂形状粉末冶金皮带轮模压致密化成型的数值模拟研究还鲜见报道。本文采用基于金属塑性力学法的金属粉末压缩致密化本构模型，模拟和分析粉末冶金皮带轮的模压致密化成型过程，预测并优化压坯的密度分布。

1 粉末冶金皮带轮模压成型数值模型

1.1铁粉压缩致密化本构模型

粉体材料压缩致密化过程中的屈服应力既与应力偏张量有关，又与应力球张量有关，其屈服行为可用椭球面屈服准则表示：

(1)

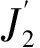
为验证本构模型在本实验条件下的有效性，开展铁粉模压实验。压制速度10 mm/s，保压时间3 s。压坯直径φ10 mm，铁粉初始相对密度ρ0=0.46，弹性模量E=210ρGPa，泊松比ν=0.93ρ-0.43。不同摩擦条件下(μ=0.05、0.08、0.1)，铁粉压制数值模拟载荷-位移曲线与实测结果对比如图1所示。可以看出，粉体与模具表面摩擦系数取0.08时，模拟与实测结果最接近，说明所采用的本构模型和摩擦条件(μ=0.08)能较好地预测铁粉的模压致密化过程。

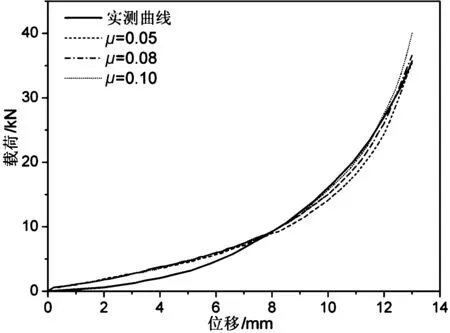
图1 铁粉压缩实测和模拟载荷-位移曲线

1.2皮带轮几何模型及网格划分

粉末冶金皮带轮压坯尺寸(单位：mm)如图2(a)所示，要求压制后相对密度大于0.89。从图中可以看出皮带轮上端面台阶高度仅2 mm，为减少模具加工，采用整体上冲。由于皮带轮压坯和载荷对称，取1/2模型计算，移粉后铁粉装填如图2(b)所示。皮带轮内孔壁、腹板、轮缘按相对密度0.92设计，即图中移粉后H1=44 mm，H2=14 mm，H3=44 mm。模拟过程中，模具设置为刚体，粉体设置为多孔塑性体，对模型齿部和倒角部位进行网格细化处理，划分为9万3 097个四面体单元和2万1 274个网格节点，如图3所示。

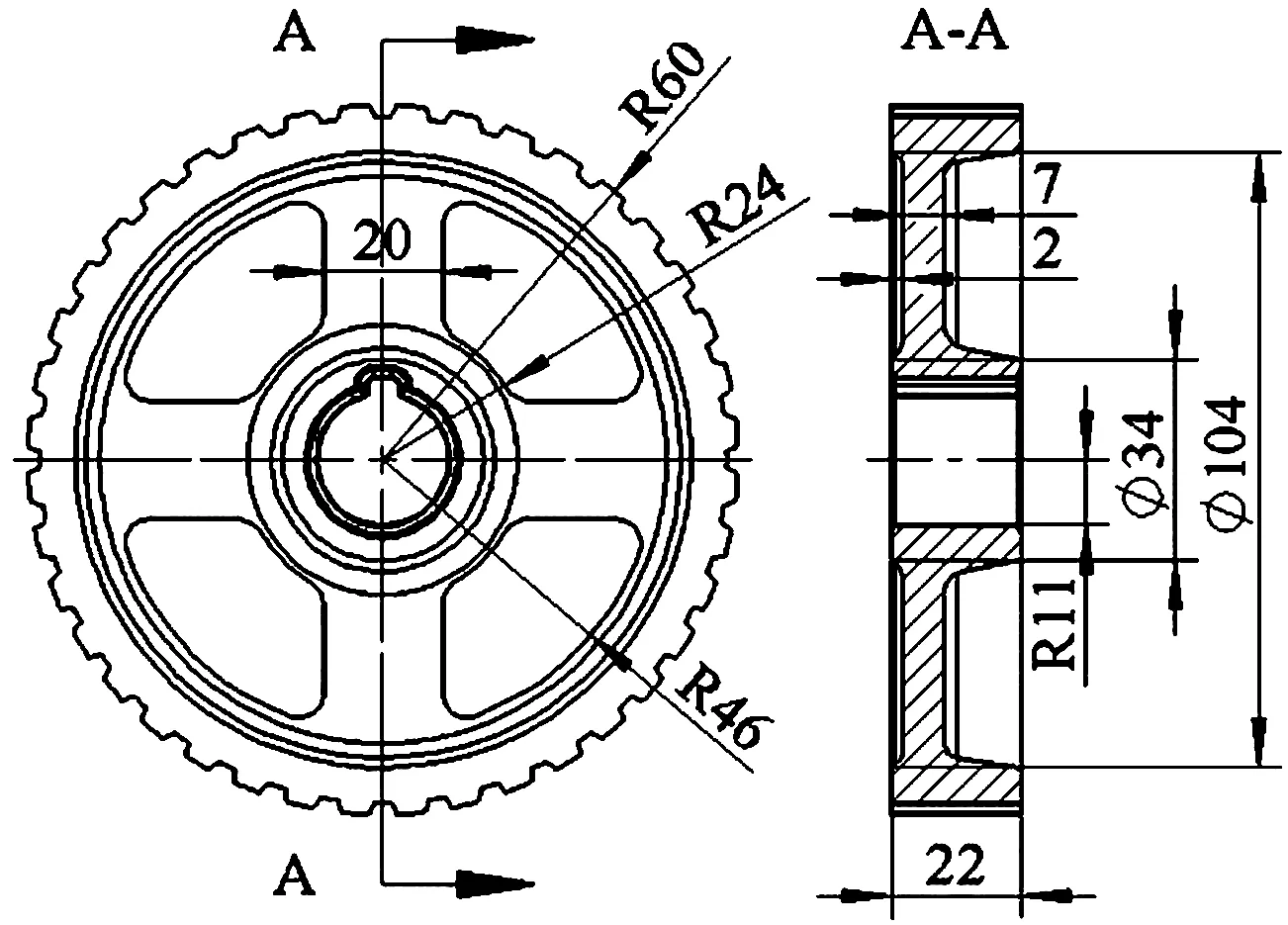
(a)

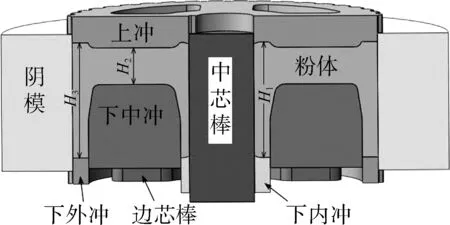
(b)

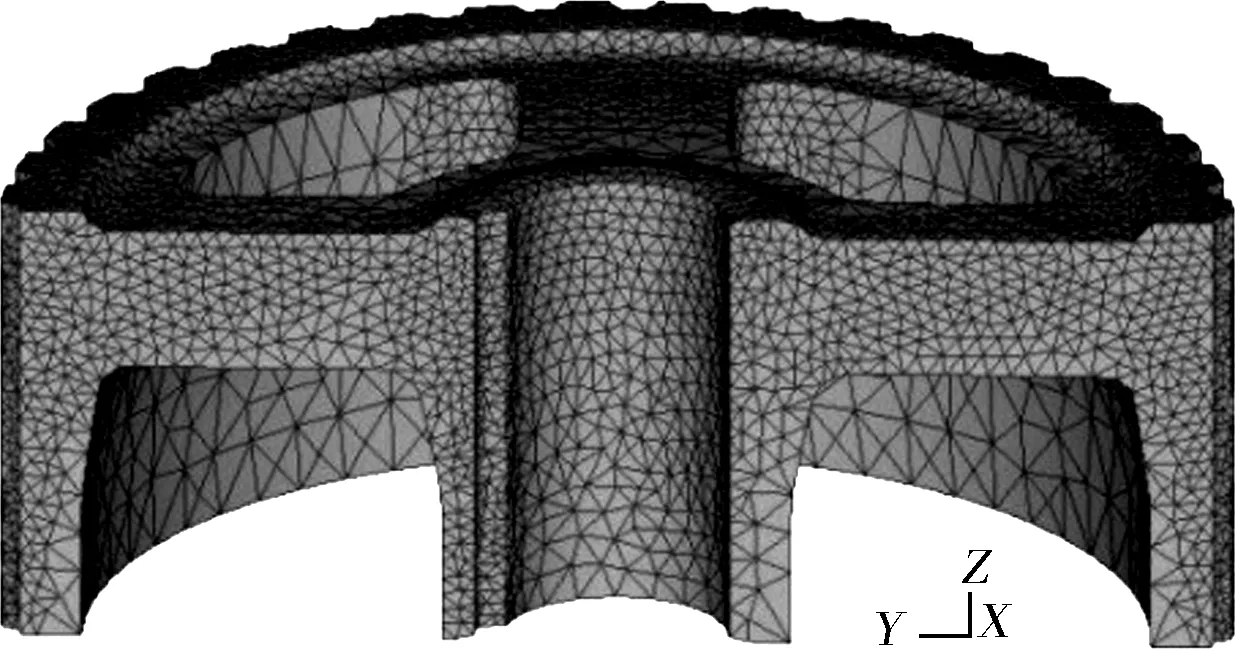
图3 粉体有限元网格划分

对有限元模拟软件进行二次开发，将上述粉体材料本构模型通过Fortran语言写入有限元分析系统，模拟粉末冶金皮带轮的模压致密化成型过程。压制方式为阴模、芯棒固定，上冲主动下压，下中冲被动压制。

2 粉末冶金皮带轮模压成型数值模拟结果与分析

2.1皮带轮模压致密化成型过程分析

图4为皮带轮压坯相对密度分布模拟结果。可以看出皮带轮各部位充填成型完整，但各部位密度分布不均匀；这是由于压制过程中皮带轮各部位压缩量不同，且模具与粉末间的摩擦力对粉末分别产生了阻碍和促进其移动致密化的不同作用。皮带轮压坯等效应变分布如图5所示，由于采用整体上冲，皮带轮上端面的内孔壁、轮缘和腹板部位的粉末在压制过程中压缩率不同，腹板部位的应变量大于内孔壁和轮缘，导致腹板部位密度较高，内孔壁和轮缘部位密度较低，尤其是内孔壁与腹板连接倒角处的粉末压缩率和应变量最小，相对密度最低。下中冲在压制过程中向下浮动，对内孔壁和轮缘部位的粉末产生向下的摩擦力作用，带动粉末向下移动，使得内孔壁和轮缘靠近下中冲位置的粉末在向下压制力和向下摩擦力的共同作用下，产生较大的应变量，压缩致密化程度增强，比远离下中冲位置的密度更高。图6示出皮带轮压坯的等效应力分布，与图4、5中压坯相对密度和等效应变分布具有相似特征，即密度和应变量大的部位，等效应力高；这是因为粉末压制过程中压缩应变量大的部位密度相应增高，导致该部位粉体的屈服应力增大。图7为各模冲压制载荷随上冲位移变化曲线。可以看出各模冲的压制载荷因其对应压制截面积不等而各不相同，压制截面积越大的模冲相应的压制载荷也越大。上冲、下内冲、下中冲和下外冲对应单位面积压制力分别为 483、626、449、587 MPa。

2.2补偿装粉量对皮带轮模压致密化成型的影响

图4 皮带轮压坯相对密度分布

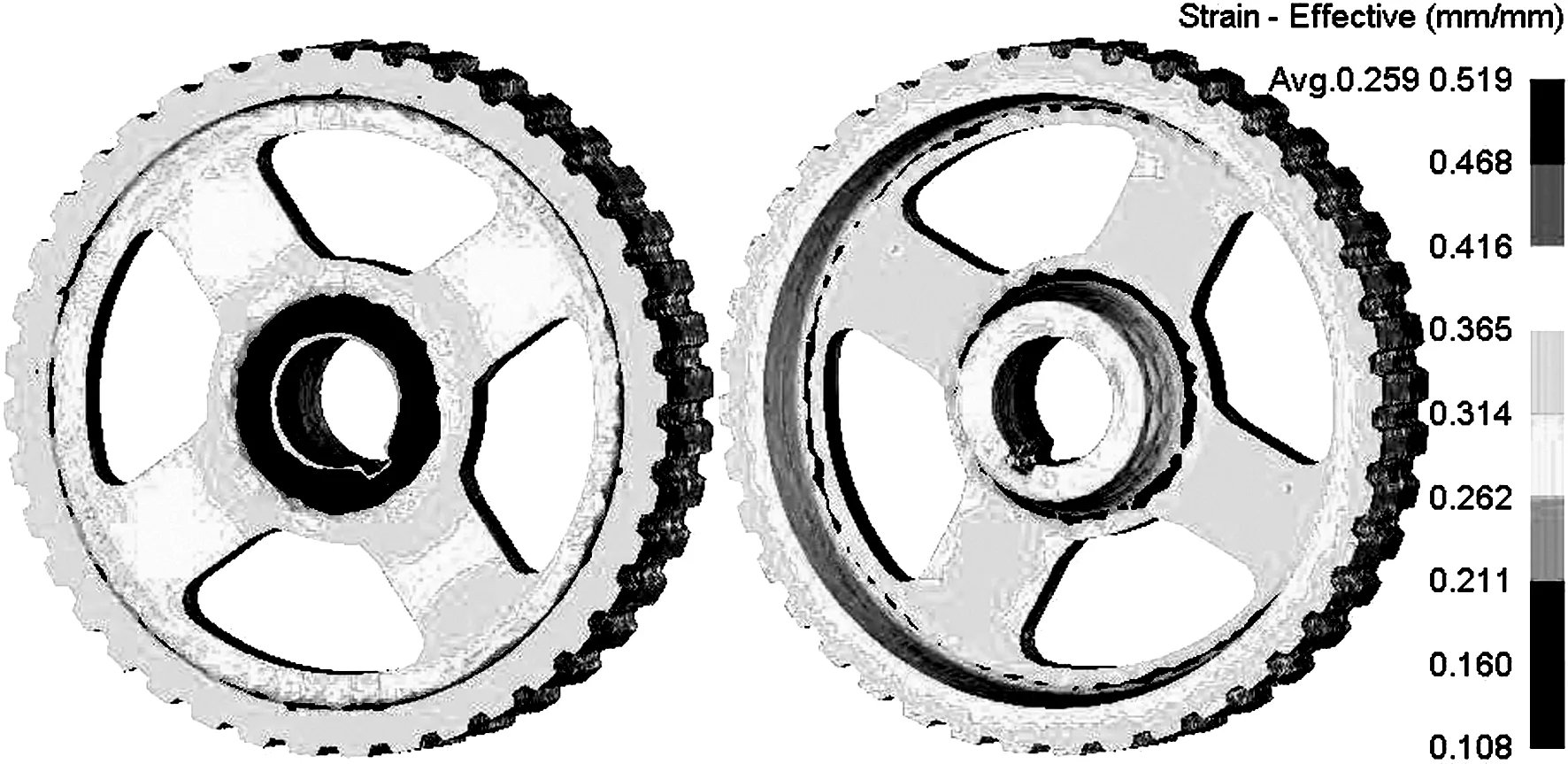
图5 皮带轮压坯等效应变分布

图6 皮带轮压坯等效应力分布

图7 各模冲压制载荷随上冲位移变化曲线

如图4所示，虽然装粉时皮带轮的内孔壁、腹板和外缘分别按压缩比0.92/0.46=2设计，但是模拟结果显示皮带轮平均相对密度仅达到0.89的最低要求，小于设计值0.92。这是由于皮带轮腹板与内孔壁、轮缘的过渡圆角处，尤其靠近下中冲斜角处的粉末压缩充填少，压缩比小于2，最终导致皮带轮平均相对密度低于0.92；因此，为增加过渡圆角和斜角处粉末的压缩率，对皮带轮内孔壁和轮缘部位装粉量进行补偿。图8示出皮带轮内孔壁和轮缘部位分别增加2 mm装粉量后压坯的相对密度分布。结合图4可以看出，补偿2 mm装粉量后，压坯最低相对密度有了较大提高，达到0.807，最高相对密度和平均相对密度也分别提高了0.023和0.031，有效改善了压坯的密度分布，但压坯平均相对密度仍低于0.92。为进一步提高压坯平均相对密度和最低相对密度，将皮带轮内孔壁补偿装粉量增加到3.5 mm，轮缘部位补偿装粉量不变，压制后相对密度分布如图9所示。可以看出皮带轮压坯平均相对密度达到设计值0.92，最低和最高相对密度也有进一步增加，有助于提高皮带轮力学性能。采用均匀性系数C分析不同装粉量对皮带轮压坯相对密度均匀性的影响[12]：

(2)

式中：ρmax、ρmin、ρavg分别为压坯的最大、最小和平均相对密度。其中均匀系数C越小，表示相对密度分布越均匀。由式(2)计算得到未补偿装粉，轮缘补偿装粉2 mm及内孔壁补偿装粉2 和3.5 mm时皮带轮压坯相对密度均匀性系数为0.223、0.190和0.183，说明补偿装粉提高并改善了皮带轮压坯的密度和密度分布。实践证明，皮带轮轮缘和内孔壁分别补偿装粉2和3.5 mm时，可压制出合格的粉末冶金皮带轮压坯，如图10所示。

图8 内孔壁和轮缘均补偿2 mm装粉量后皮带轮压坯相对密度分布

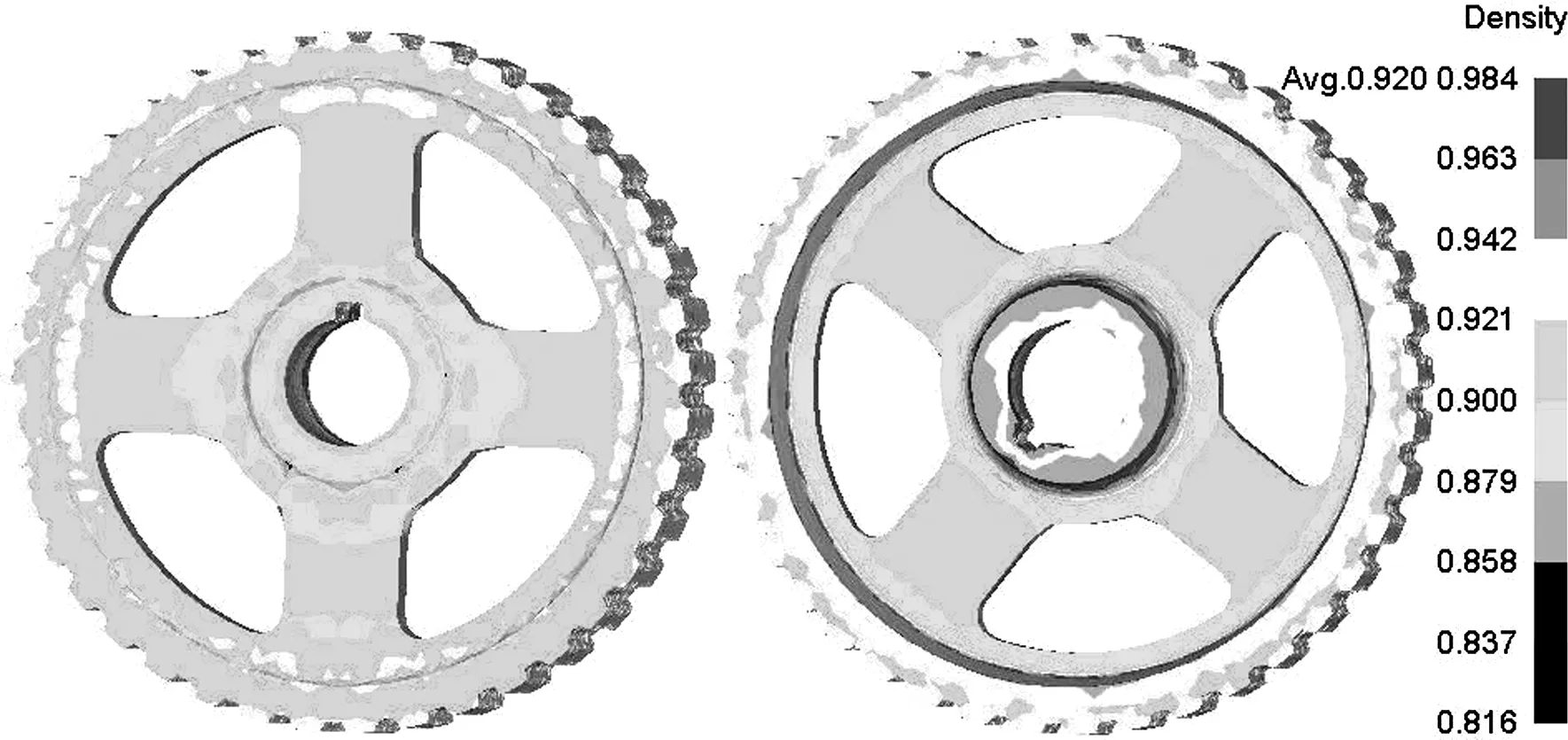
图9 内孔壁补偿3.5 mm及轮缘补偿2 mm装粉量后皮带轮压坯相对密度分布

图10 粉末冶金皮带轮压坯

3 结论

1)基于金属塑性力学法的有限元数值模拟技术能有效地模拟和预测铁粉的压缩致密化过程，粉体与模具间摩擦因数取0.08时更接近实测结果。

2)粉末冶金皮带轮压制过程中，由于压坯各部位压缩率不同，以及粉体与模具间的摩擦力作用不同，导致压坯密度分布不均匀。压缩率高的部位，应变量大，密度高，等效应力也增大。摩擦力方向与压制方向相同时，促进粉体致密化，反之阻碍粉体致密化。

3) 通过数值模拟预测粉末冶金皮带轮的压制过程，对压坯的低密度区进行补偿装粉，可有效提高和改善粉末冶金皮带轮压坯的密度和密度分布，优化压制工艺，对产品的实际压制过程具有较好的指导意义。

[1]韩凤麟. 亚洲粉末冶金零件产业发展与现状[J]. 新材料产业, 2008(4): 25-32.

[2]刘咏, 黄伯云, 龙郑易, 等. 从PM2004看世界粉末冶金的发展现状[J]. 粉末冶金材料科学与工程, 2005, 10(1): 10-20.

[3]王崇琳. 论粉末冶金材料的密度测定[J]. 粉末冶金工业，2010,20(6): 1-4.

[4]李元元, 夏伟, 周照耀, 等. 基于有限变形弹塑性本构方程的金属粉末压制成形力学建模及数值模拟[J]. 数字制造科学, 2009,7(2): 1-28.

[5]欧阳洪武，何世文，韦嘉，等. 装粉方式对钛粉压制成形影响的数值模拟[J]. 中国有色金属学报，2004, 14(8): 1318-1323.

[6]王德广，吴玉程，焦明华，等. 不同压制工艺对粉末冶金制品性能影响的有限元模拟[J]. 机械工程学报，2008, 44(1): 205-211.

[7]Li Yuanyuan, Zhao Weibin, Zhou Zhaoyao, et al. Coupled Mechanical and Thermal Simulation of Warm Compaction[J]. Trans Nonferrous Met Soc China , 2006, 16(2): 311-315.

[8]Kim K T ， Lee H T. Effect of Friction Between Powder and a Mandrel on Densification of Iron Powder during Cold Isostatic Pressing[J]. Int J Mech Sci , 1998,40(6): 507-519.

[9]Song Yi, Li Yuanyuan, Zhou Zhaoyao, et al. Improved Model and 3D Simulation of Densification Process for Iron Powder[J]. Trans Nonferrous Met Soc China , 2010, 20(8): 1470-1475.

[10]Lee S C ， Kim K T. Densification Behavior of Aluminum Alloy Powder under Cold Compaction[J]. Int J Mech Sci , 2002,44(7): 1295-1308.

[11]Zhou Rui, Zhang Lianhong, He Baiyan, et al. Numerical Simulation of Residual Stress Field in Green Powder Metallurgy Compacts by Modified Drucker-Prager Cap Model[J]. Trans Nonferrous Met Soc China , 2013,23(8): 2374-2382.

[12]章凯, 李萍, 王成, 等. 钼粉末温压扭成形致密化行为模拟研究[J]. 粉末冶金工业，2010, 20(5): 31-34.

(编校：夏书林)

NumericalSimulationofDensificationandFormingforPMPulleyduringCompaction

GUO Biao, WEI Xiao-wei, AO Jin-qing, XIAO Xian-tong

(SchoolofMaterialsScienceandEngineering,XihuaUniversity,Chengdu610039China)

The program of powder material constitutive model was developed in Fortran language and the model was implanted into finite element analysis system to simulate the compaction and densification process of iron powder. The validity of the model was verified by comparing the load strokes from simulation with experimental result. Subsequently, the model was used to simulate and analysis the forming and densification process of powder metallurgy(PM) pulley during compaction, and the density distribution of PM pulley was predicted. The density and its distribution were improved by compensating the powder-filling amount in low-density zone. In practice, the qualified PM pulley was compacted by using the optimized process, which indicates the optimized process can be taken as a reference for the compaction process design of this kind of parts.

powder metallurgy; pulley; density distribution; numerical simulation

2014-11-14

汽车高性能材料及成形技术省高校重点实验室开放研究基金资助项目(SZJJ2014-055)。

郭彪(1984—)，男，讲师，博士，主要研究方向为高性能粉末冶金材料及成形技术。

TF124

：A

：1673-159X(2015)06-0077-04

10.3969/j.issn.1673-159X.2015.06.016