求解广义BBM-Burgers方程的一个两层非线性守恒差分格式

(西华大学理学院，四川 成都 610039)

·基础学科 ·

求解广义BBM-Burgers方程的一个两层非线性守恒差分格式

胡劲松, 王婷婷, 陈 涛

(西华大学理学院，四川 成都 610039)

对广义BBM-Burgers方程的初边值问题进行了数值研究，提出一个两层非线性Crank-Nicolson差分格式，格式合理地模拟方程本身的一个守恒量，得到差分解的先验估计和存在唯一性，并利用能量方法分析该格式的二阶收敛性与无条件稳定性。

广义BBM-Burgers方程；差分格式；守恒；收敛性；稳定性

BBM方程是由Benjamin等[1]为描述非线性弥散系统中长波的单向传播而提出来的。它是对用来描述浅水波损耗现象的KdV方程的一个修改，因此对这类问题的研究有重要的理论价值。关于广义BBM-Burgers方程的解的存在唯一性、收敛性以及解的大时间渐近性状态等都有了很多研究[2-5]。由于广义BBM-Burgers方程的解析解很难求出，所以研究其数值解就非常有意义。Kamel Al-Khaled 等[6]利用Adomian分解方法对广义BBM-Burgers方程的数值解进行了研究；文献[7]利用Fourier 拟谱方法讨论了广义BBM-Burgers方程的周期初边值问题的数值解。

本文考虑如下一类广义BBM-Burgers方程的初边值问题：

ut-uxxt+ux-uxx+upux=0，x∈(xL,xR)，t∈(0,T];

(1)

u(x,0)=u0(x)，x∈[xL,xR];

(2)

u(xL,t)=u(xR,t)=0，t∈[0,T]。

(3)

其中：p≥1为正整数；u0(x)是已知函数。由于方程(1)的物理渐近边界条件为：当|x|→时，u→0，ux→0，所以不难验证，初边值问题(1)—(3)具有如下守恒量：

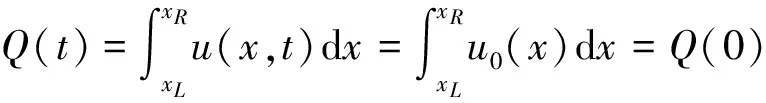
(4)

其中Q(0)为仅与初始条件有关的常数。

文献[8-9]用有限差分方法对问题(1)—(3)进行数值方法研究，分别提出三层的二阶差分格式，但都没有模拟守恒量(4)。本文利用文献[10-11]处理广义正则长波(GRLW)方程和广义对称正则长波(GSRLW)方程的技巧，对问题(1)—(3)提出了一个两层非线性Crank-Nicolson差分格式，格式合理地模拟问题的守恒量(4)，讨论了其差分解的存在唯一性并分析了格式的收敛性和稳定性。

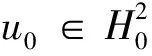
证明令

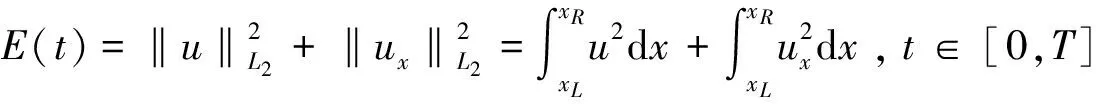
并注意到(3)式和ut-uxxt=-ux-upux+uxx，有

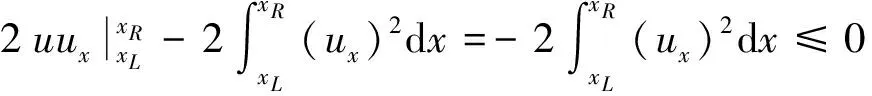
故E(t)关于时间t是单调递减，即

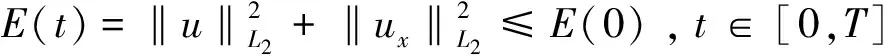
也即

‖u‖L2≤C，‖ux‖L2≤C；

再由Sobolev不等式有‖u‖L≤C。

1 差分格式及其守恒律

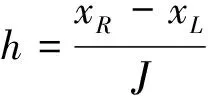
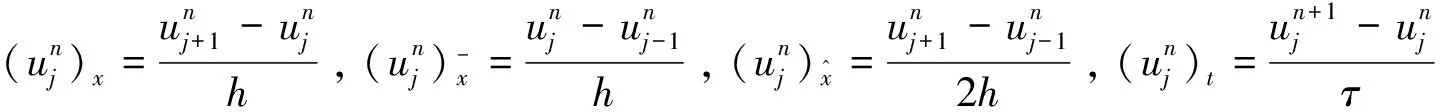
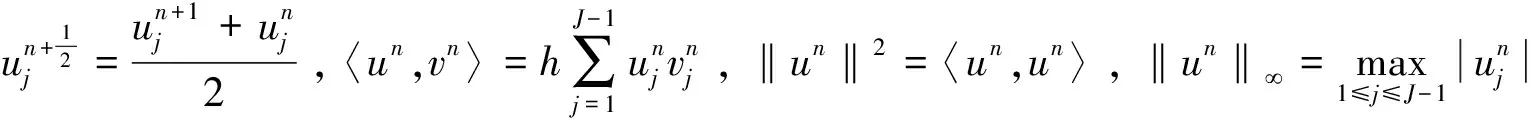
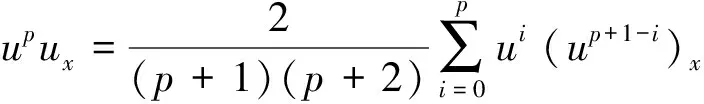
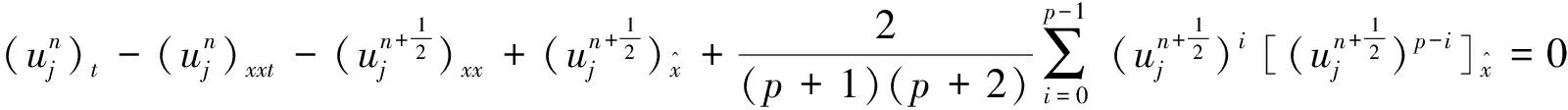
j=1, 2, …,J-1，n=1, 2, …,N;

(5)

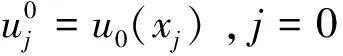
(6)

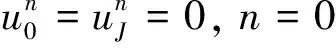
(7)

为了分析方便，本文中定义

差分格式(5)—(7)对守恒量(4)的数值模拟如下：

定理1 差分格式(5)—(7)具有如下离散守恒律，即

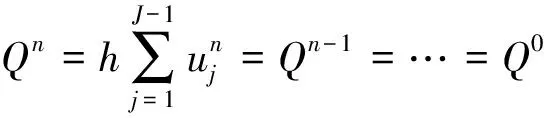
(8)

证明将(5)式两端乘以h然后对j从1到J-1求和，得

(9)

由边界条件(7)和分部求和公式[12]有

(10)

(11)

当p为奇数时，有

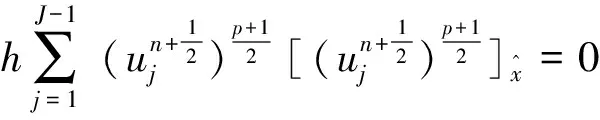
(12)

于是由式(10)—(12)有

(13)

又

(14)

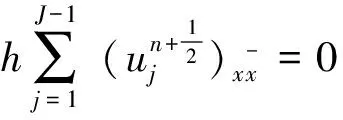
(15)

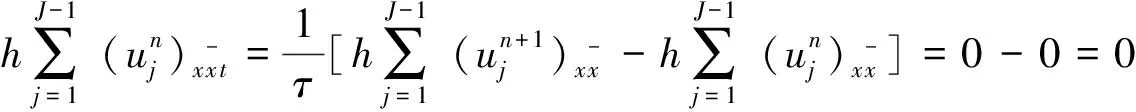
(16)

将式(13)—(16)代入式(9)，整理得

(17)

由Qn的定义，将式(17)递推可得式(8)。

2 差分格式的先验估计

引理2 (离散Sobolev不等式[12])存在常数C1和C2使得‖un‖≤C1‖un‖+C2‖‖。

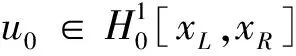
(18)

由于

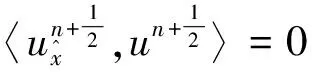
(19)

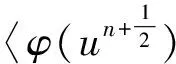
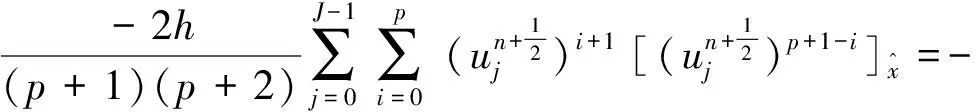
即

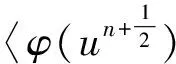
(20)

所以，由式(18)—(20)得

即

由此可得

再由引理2得

‖un‖≤C。

3 差分格式的可解性

引理3 (Brouwer不动点定理[13])设H是有限维内积空间，g：H→H是连续算子且存在α>0使得∀x∈H，‖x‖=α有〈g(x),x〉>0，则存在x*∈H，使得g(x*)=0且‖x*‖≤α。

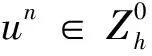
证明用数学归纳法。由式(6)知，当n=0时，差分解存在；假设当nN-1时，存在u0,u1,…,un满足差分方程(5)—(7)，下面证明存在un+1满足差分方程(5)—(7)。

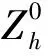
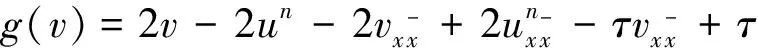
(21)

将式(21)与v作内积，并注意到类似于式(19)和式(20)，有

于是

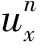
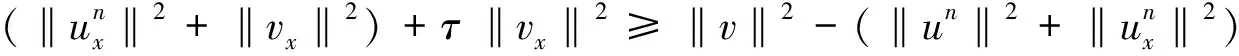
4 差分格式的收敛性与稳定性及其解的唯一性

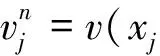
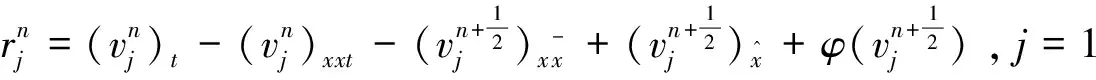
(22)

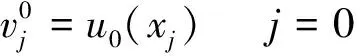
(23)

(24)

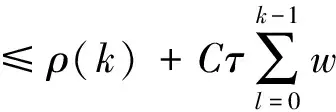
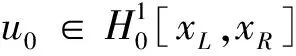
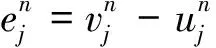
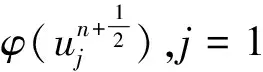
(25)

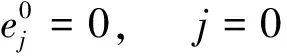
(26)

(27)

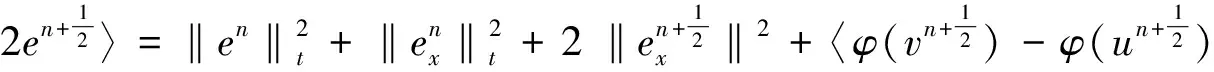
(28)

由引理1、定理2，以及 Cauchy-Schwarz不等式，有

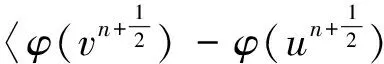
(29)

(30)

Bn+1-BnCτ(Bn+1+Bn)+τ‖rn‖2，

即

(1-Cτ)[Bn+1-Bn]≤2CτBn+τ‖rn‖2。

只要取适当小的τ，满足1-Cτ>0，就有

Bn+1-Bn≤CτBn+Cτ‖rn‖2。

(31)

对式(31)从0到n-1求和得

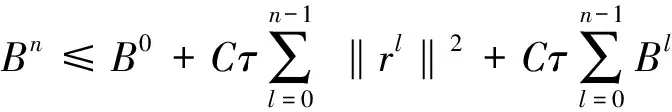
由式(26)有

B0=O(τ2+h2)2。

又

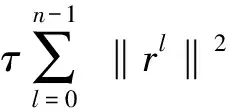
于是

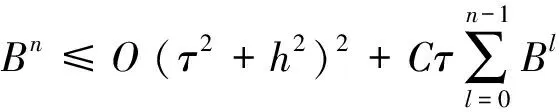
由引理4可得

Bn≤O(τ2+h2)2，

即

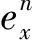
最后由引理2有‖en‖≤O(τ2+h2)。

与定理4类似，可以证明：

定理5 在定理4的条件下，差分格式(5)—(7)的解un以‖·‖关于初值无条件稳定。

定理6 差分格式(5)—(7)的解是唯一的。

[1]Benjamin T B, Bona J L,Mahony J J.Model Equations for Long Waves Nonlinear Dispersive System[J].Phil Trans R Soc London,1972,A272：47-78.

[2]Mei M.Large-time Behavior of Solution for Generalized Benjamin-Bona-Mahony-Burgers Eqation[J].Noninear Analysis,1998(33)：699-714.

[3]Mei M.Decay Rates of Solutions for Generalized Benjamin-Bona-Mahony-Burgers Eqation [J]. J Differential Equations,1999,158：314-340.

[4]ZHAO Hui-jiang,XUAN Ben-jin.Existence and Convegence of Solutions for Generalized BBM-Burgers Eqation with Dissipative Terms[J].Noninear Analysis,1997(28)：1835-1849.

[5]SHANG Y D，G B L. Exponential Attractor for the Generalized Burgers-BBMEquation[J]. Chinese J of Engine Math,2004,21(3)：435-442.

[6]Al-Khaled K, Momani S, Alaweh A. Approximate Wave Solution for Generalized Regularized Enjamin-Bina-Mahnoy-Burgers Equations [J]. Appl Math & Commput,2005,171：281-292.

[7]尚亚东.解广义的Burgers-BBM方程的Fourier 谱方法及误差估计[J].工程数学学报，1998,15(4)：13-20.

[8]胡劲松. 广义BBM-Burgers方程的有限差分逼近[J].黑龙江大学学报：自然科学版,2010, 27(5)： 651-654.

[9]Che Hai-tao , Pan Xin-tian , Zhang Lu-ming , et al. Numerical Analysis of a Linear-Implicit Average Scheme for Generalized Benjamin-Bona-Mahony-Burgers Equation[J].Journal of Applied Mathematics Volume， 2012, Article ID 308410, 14 pages.

[10]王廷春,张鲁明.求解广义正则长波方程的守恒差分格式[J].应用数学学报,2006, 29(6)：1091-1098.

[11]聂涛,王廷春,张鲁明.对称正则长波方程的守恒差分算法[J].高等学校计算数学学报,2007, 29(3)：257-266.

[12]Hu B,Xu Y.Hu Crank-Nicolson Difference Scheme for the Rosenau-Burgers Equation[J]. Appl Math Comput,2008,204：311-316.

[13]Browder F E.Existence and Uniqueness Theorems for Solutions of Nonlinear Boundary Value Problems[J].Proceedings of Symposia in Applied Mathematics,1965,17：24-49.

(编校：叶超)

TwoLevelNonlinearConservativeDifferenceSchemeforSolvingGeneralizedBBM-BurgersEquation

HU Jin-song, WANG Ting-ting, CHEN Tao

(SchoolofScience,XihuaUniversity,Chengdu610039China)

In this paper, a two level nonlinear Crank-Nicolson difference scheme is proposed. The scheme provides a numerical solution to the initial boundary value problem of general BBM-Burgers equation. A conservative variable of the equation is simulated well with the scheme. In the simulation, the prior estimate and uniqueness of the solution are also obtained. In addition, the second order convergence and unconditional stability are proved by using energy analysis.

generalized BBM-Burgers equation；difference scheme；conservation； convergence； stability

2013-11-13

四川省教育厅青年基金(11ZB009)

胡劲松(1973—)，男，教授，博士，主要研究方向为偏微分方程数值解。

O241.8

：A

：1673-159X(2015)03-0089-05

10.3969/j.issn.1673-159X.2015.03.018