径向导叶式多级泵单级叶轮切割的三维数值模拟

(兰州理工大学能源与动力工程学院, 甘肃 兰州 730050)

·能源与环境·

径向导叶式多级泵单级叶轮切割的三维数值模拟

杨从新，富 友

(兰州理工大学能源与动力工程学院, 甘肃 兰州 730050)

为探究径向导叶式压出室离心泵叶轮切割后性能的变化，基于N-S方程、标准k-ε湍流模型和SIMPLE算法对MD-280-42×4多级离心清水泵单级叶轮外径切割进行三维湍流数值计算，分析不同切割量下径向导叶式离心泵外特性和内部流动变化。结果表明：在设计工况(Qd=0.078 m3/s)下，随着切割量的增加，径向导叶式离心泵的水力效率、轴功率均呈现下降趋势；在相同小流量工况下，随着切割量的增加，叶轮与导叶间隙和反导叶流道处流动损失逐渐减小，水力效率呈现上升趋势；在相同大流量工况下，随着切割量的增加，正反导叶流道流动均匀性受到较严重破坏，产生了较大的能量耗散，水力效率明显下降。

叶轮切割；径向导叶；多级离心泵；反导叶；数值模拟

叶轮外径的取值是影响泵性能的重要因素，工程上广泛采用切割叶轮的方法来改变泵的运行性能。

国内外学者对此展开过诸多研究，并通过大量理论与实践的对比，对不同比转数、不同叶轮切割方式的切割定律进行了验证和修正[1-4]。

对导叶式多级离心泵而言，其流道由正导叶、环形空间和反导叶组成。其正反导叶均为周向均布，正导叶起压水室的作用，反导叶除了有降低流速、消旋等作用外，还起着下一级吸水室的作用，同时其压出室特点与螺旋形压出室有较为明显区别。国内外学者大多集中研究多级泵转子动力学分析、多级泵的轴向力径向力、不同导叶数与叶片数的匹配与优化，而对径向导叶式压出室的叶轮切割的特性研究相对较少[5-6]。

本文以径向导叶式压出室的离心泵单级叶轮为研究对象，对不同叶轮外径下的径向导叶式离心泵进行三维湍流流动数值模拟，研究叶轮外径变化对其性能的影响，并比对分析其内部流动的变化。

1 几何模型及边界条件

1.1几何模型

本文以改进的MD280-42×4多级离心清水泵为研究对象，主要设计参数如下：转速n=1 480 r/min，流量Q=280 m3/h，效率η=77%，比转数ns=90。如图1所示，此多级泵叶轮为轴对称分布，以这种形式布置的叶轮可以提高泵的轴向平衡能力，并代替原泵的专有平衡部件，如平衡盘、平衡鼓等，从而使整体结构更加紧凑。由于考虑到单级切割会对整机组的性能造成影响，使得无法准确地说明径向导叶式压出室叶轮切割后性能的变化，故选取整机组首级做为单独研究对象，泵单级的几何模型如图2所示。其中单级叶轮及导叶流道的设计参数如下：单级扬程H=42 m，叶轮叶片数Z=7，叶轮直径D2=360 mm，叶轮出口宽度b2=26 mm，导叶叶片数Z2=8，反导叶叶片数Z3=8，导叶入口角а3=12°。切割量如表1所示。

1—前部吸入段；2—首级叶轮；3—首级导叶；4—次级叶轮；5—次级压出室；6—第3级吸入段；7—第3级叶轮；8—第3级导叶；9—第4级叶轮；10—第4级压出室。

图1 MD280-42×4结构示意图

图2 泵的几何模型

表1 切割后外径参数(15%为行业规定的最大切割量)

切割量/%直径/mm0360．02352．84345．66338．48331．2切割量/%直径/mm10324．012316．814309．615306．0

1.2网格划分

计算区域网格划分采用GAMBIT软件进行，其中入口及出口延伸段用六面体网格进行绘制，叶轮及导叶流道采用四面体网格进行绘制。

1.3控制方程及边界条件

对不可压流体相对定常流动，雷诺时均方程为：

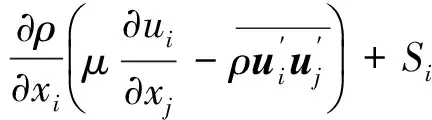
标准k-ε湍流模型方程如下：

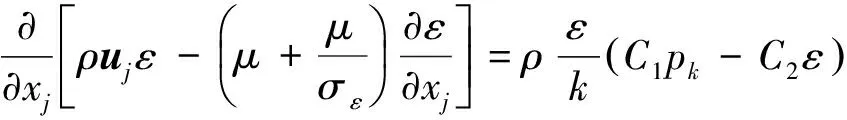
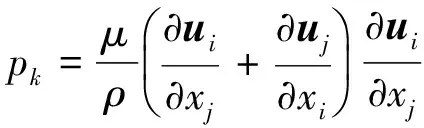
采用有限体积法对控制方程在网格上进行离散，离散采用二阶迎风格式，在求解压力-速度耦合方程时采用SIMPLE算法。泵进口条件设置为速度进口；泵出口采用自由出流边界条件；在壁面处采用无滑移边界条件，并采用标准壁面函数对标准的k-ε模型进行修正。

2 计算结果及分析

2.1性能预测

图3为整机组外特性曲线试验值与模拟值的对比曲线。可以看出：由于模拟时忽略了泄漏损失、机械损失，故模拟后外特性值大于实际试验值；但模拟值与试验值的效率与扬程变化趋势基本相同，说明了数值手段的准确性。

图3 整机组模拟与试验的性能曲线对比

图4为径向导叶式多级泵单级外特性曲线。由于单级切割后对泵性能的影响会在后几级中被一定程度地放大，影响到本文对此类压出室叶轮切割影响的探讨；故下文均为单级单独切割的分析，其偏差对比均为与图4所用模型相匹配。

图4 单级模型性能曲线

2.2切割叶轮外径对单级外特性的影响

对径向导叶式离心泵单级叶轮进行了8次切割，由图5、图6可以看出：随着切割量的增加，扬程、轴功率均呈现下降趋势；但对比切割定律反算后，其值与设计工况下(Q=0.078 m3/s)的扬程有较大差距，其偏差范围为5.613 6%～23.613%，平均偏差为16.703 6%。

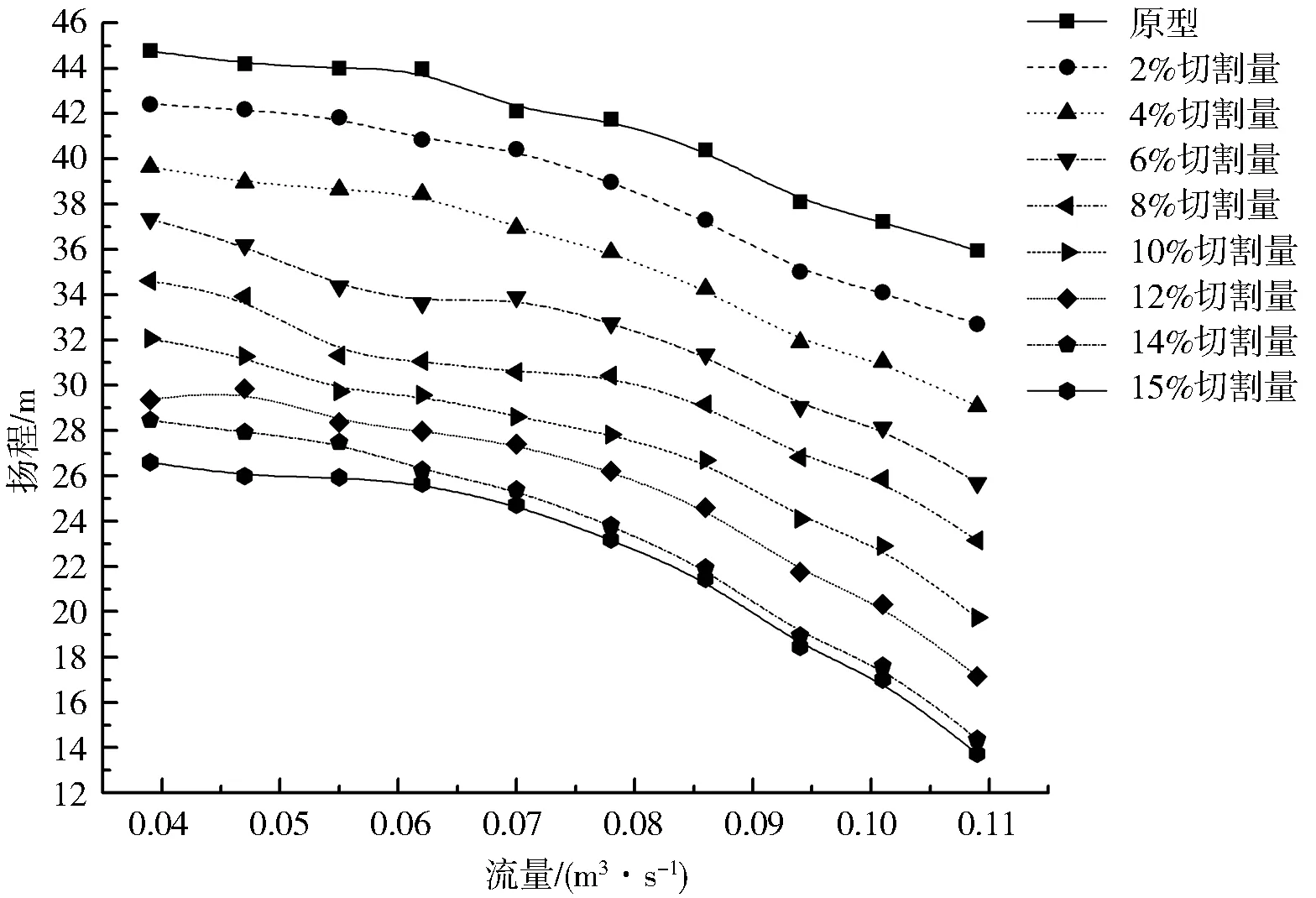
图5 不同切割量下流量-扬程特性曲线

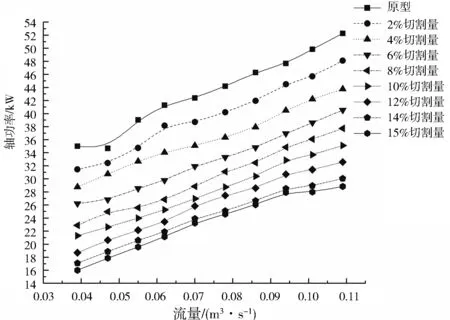
图6 不同切割量下流量-功率特性曲线

叶轮切割后出口宽度和出口角的变化如图7所示。可以看出，随着切割量的增加，叶轮的出口宽度、出口角发生了明显的变化，说明切割定律成立的先决条件已经被破坏，同时叶轮流道的几何相似被破坏，也有可能是产生较大偏差的原因。

图7 叶轮切割后出口宽度b2和出口角β2的变化

图8为流量大于设计工况时，不同流量下水力效率随切割量的变化曲线。可以看出随着切割量的增加，泵的水力效率呈现下降趋势，且下降程度随流量的增加而加大，效率最大下降量为22.497 5%。

图8 大流量工况不同切割量下水力效率变化曲线

图9为流量小于设计工况时，不同流量下水力效率随切割量的变化曲线。可以看出随着切割量的增加，泵的水力效率反而呈现上升趋势，其中最大上升量为14.58%，平均上升量为9.274 5%。

图9 小流量工况不同切割量下水力效率变化曲线

由于压水室的水力损失和叶轮出口的绝对速度有关，且压水室的过流断面的设计也是在设计流量的基础上进行设计，以保证在设计流量下，叶轮出口的绝对速度方向和大小与压出室的进口流速的大小和方向有较好的一致性[7]。当泵在不同工况下运行时，叶轮出口绝对速度大小和方向发生变化，与它所对应压出室的进口液流产生了差异。

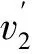
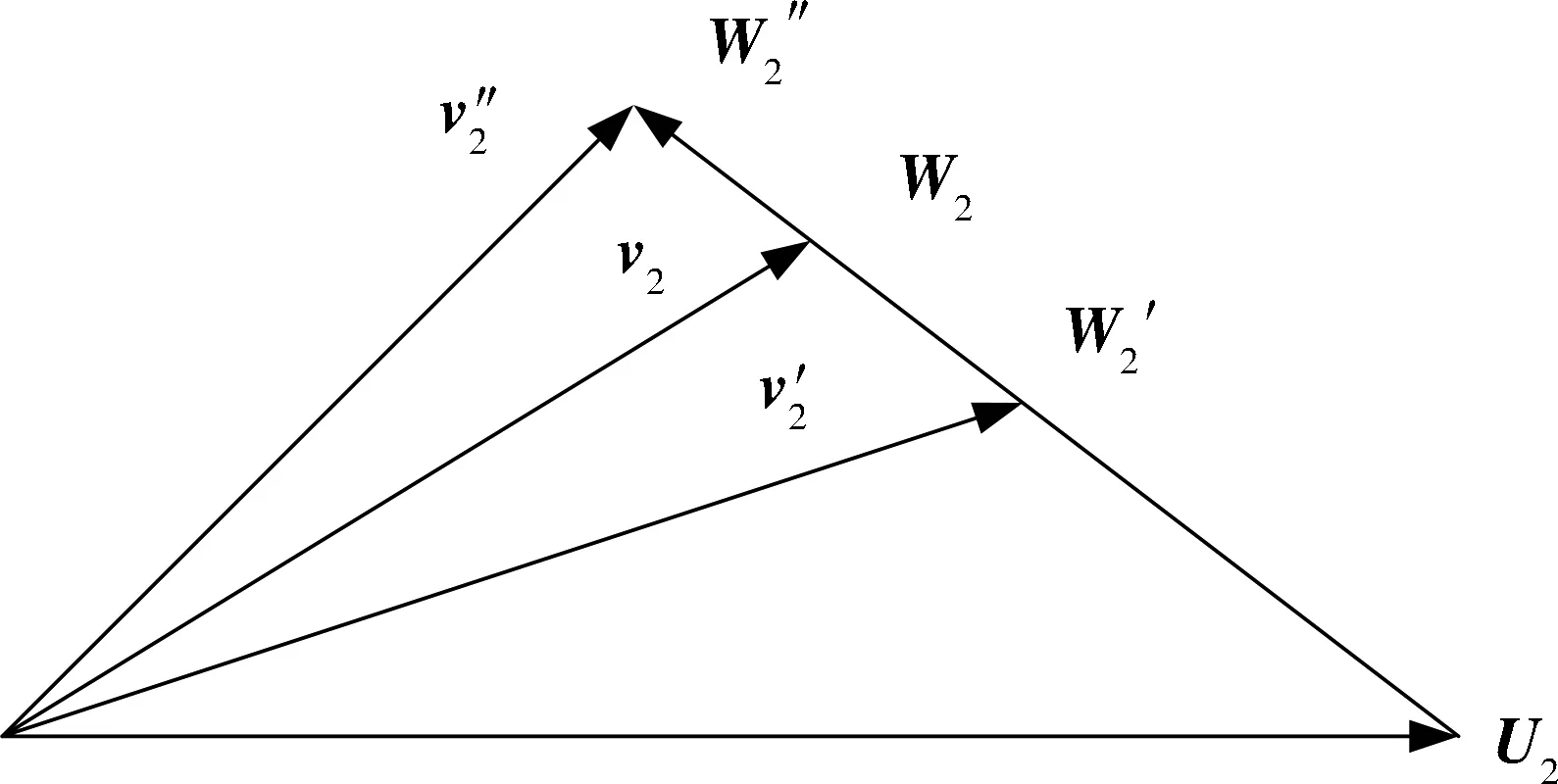
图10 不同流量下速度三角形

在小流量工况下，叶轮出口处液流速度较高，而导叶流道内速度较低，液流经过两流道时，由于速度的急变，同时与导叶前段造成冲击，必然产生漩涡，造成能量损失。

随着切割量增大，在小流量下，会在叶轮出口与导叶入口间隙处形成一定厚度的液流环。此液流环起到缓冲作用，从而使得两个流道内流体流速及流动方向更趋近于相近，减少由于速度的冲击而产生能量的损失；因此，随着切割量的增大，在小流量工况下，水力效率反而随着切割量而递增。

而在当流量大于设计工况后，由于速度变化趋势与小流量状态下相反，故液流环在小流量下的作用已被消除。在随着切割量的增加过程中，叶轮对于流体的控制能力逐渐减弱，叶轮出口处圆周速度逐渐增加，间隙处产生一定的环流导致流动损失增加。同时，由于叶轮切割量的增加，流道长度缩短，叶轮流道内扩散度逐渐加剧，最终导致液流产生脱流，形成死水区，同时造成内流场压力分布不均等现象，从而导致水力效率的下降。

2.3切割叶轮外径对单级内部流场的影响

2.3.1 正导叶内部流场分析

如图11所示，取小流量工况(Q=0.039 m3/s、Q=0.055 m3/s)，对不同切割量(0、2%、6%、10%、14%切割量)下的模型内部流场进行比对。发现同一流量下，随着切割量的上升，速度场分布逐渐趋于均匀，叶轮流道与导叶流道间隙处涡流逐渐减少，内流速度变化梯度逐渐减小。

Q=0.039 m3/s

Q=0.055 m3/s

图11 小流量下不同外径的速度分布

取小流量工况(Q=0.039 m3/s、0.055 m3/s)，原型与14%切割量下2种模型，对半径分别为120、140 、160 、180 、200 、220 、240 、250 mm(最大半径257 mm)位置处的湍流动能值进行比较，具体数据如图12所示。

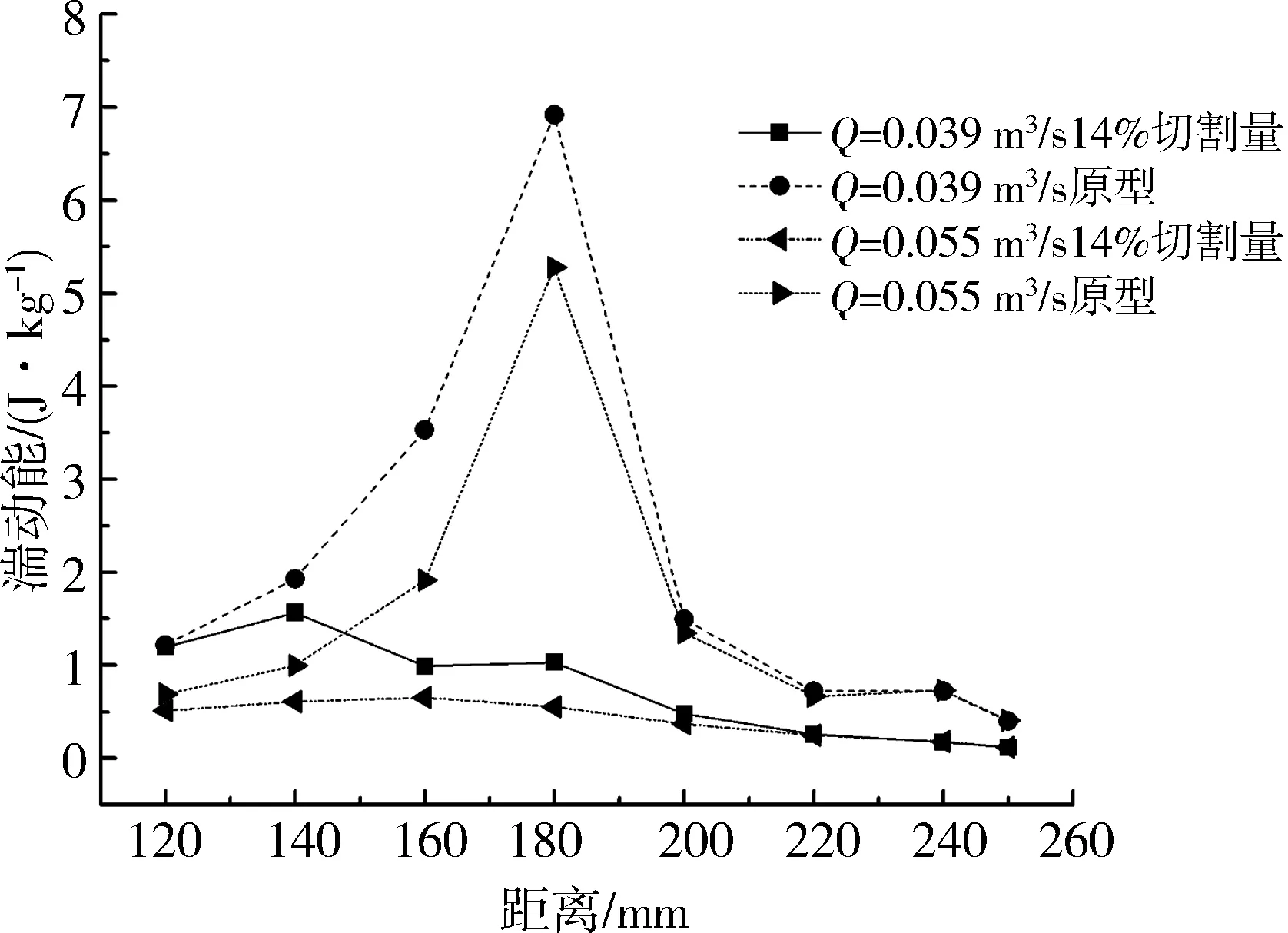
图12 不同直径位置湍流动能分布

如图12所示，随着切割量的增大，叶轮流道与导叶流道间隙处(半径180 mm位置)，14%切割量下的湍流动能值远小于原型泵在此处的数值，说明在小流量下，随着切割量的增大，叶轮流道与导叶流道间隙处速度梯度逐渐减小，从而减少了间隙处的能量耗散。

如图13所示，取流量等于、大于设计工况(Q=0.078 m3/s、0.109 m3/s)时，对2%、6%、10%、14%叶轮切割量下内流场静压图进行比对。发现在相同流量下，随着切割量的递增，流场内压力分布越来越不均匀，导叶流道入口产生低压区。说明在导叶前段处产生了严重的流动分离，由于径向导叶的特殊结构，其布置特点相当于多个蜗壳隔舌作用共同干扰压出室的流动；因此，在切割量增大的同时，在导叶前端，由于冲击的作用，产生了较为明显的能量损失，导致在大于设计流量下随着切割量的递增，泵的水力效率严重下降。

Q=0.109 m3/s

2.3.2 反导叶内部流场分析

由于湍流动能的变化能很好地说明流场内能量的耗散[8]，故选取反导叶距轴线240 、220 、200 、180 、160 、140 、120 、100 mm处位置，监测不同切割量下反导叶流场的湍流动能变化，具体数据如图14所示。

由图14可以看出，在Q=0.039 m3/s时，反导叶入口处湍流动能值随切割量的增加而逐步下降，切割量的增加均使反导叶内流场能量耗散降低。其中在120 、100 mm位置处略有上升趋势，其原因是由于液流由径向突然变成轴向，速度方向的急剧变化造成了较大的能量耗散。

在Q=0.078 m3/s(设计工况)时，可以看出随着切割量的增加，反导叶内流场湍流动能具有较好的下降趋势。

在Q=0.109 m3/s时，可以看出随着切割量的增加，反导叶内流场湍流动能值随着切割量的增加呈先下降，后上升的趋势。在切割量为2%～6%时，反导叶内流场湍流动能的值随切割的增加呈现下降趋势；在切割量大于6%以后，反导叶内流湍流动能随切割量的增加而上升：因此大流量工况下，随着切割量的增加导致效率下降有如下原因：1)叶轮对流体做功能力下降；2)间隙增大产生环流；3)反导叶内能量耗散随切割量逐渐增加。

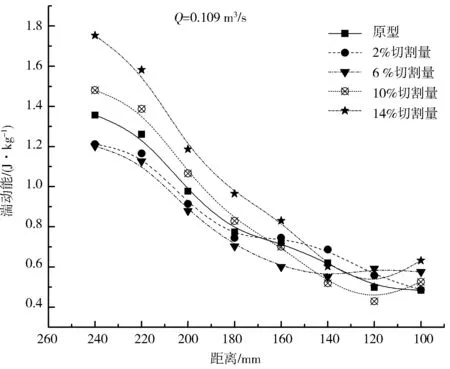
图14 反导叶不同直径位置湍流动能分布

图15为在Q=0.039 m3/s、=0.109 m3/s流量下反导叶速度矢量随切割量的变化图。可以看出反导叶内部流动变化与反导叶不同位置湍动能变化趋势有较好的一致性。

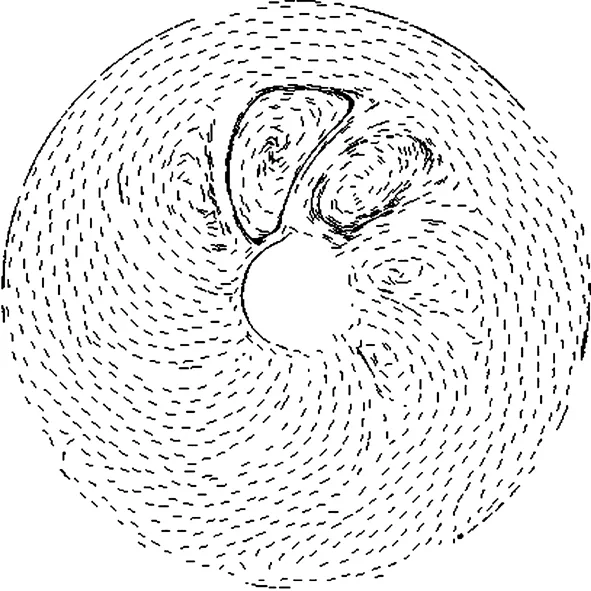
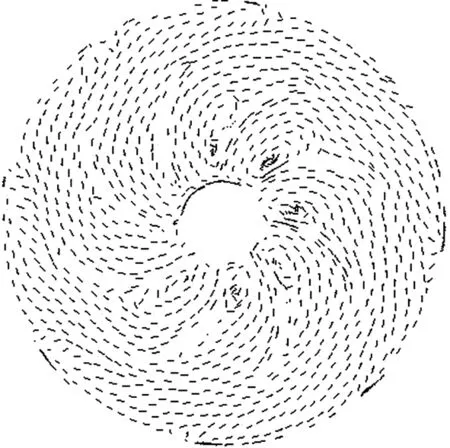
Q=0.039 m3/s

Q=0.109 m3/s

图15 反导叶不同切割量下速度矢量图

3 结论

本文通过数值计算的方法对叶轮不同切割量下的MD-280-42×4径向导叶式多级离心泵的单级进行三维湍流数值模拟，结果表明：

1)在设计工况(Qd=0.078 m3/s)下，随着切割量的加大，径向导叶式离心泵的水力效率、轴功率均呈现下降趋势，但对比切割定律，扬程平均偏差为16.703 6%，其偏差较大的原因可能为叶轮流道几何相似的破坏。

2)在相同小流量工况(Q

3)在相同大流量工况(Q>Qd)下,随着切割量的增加，正导叶进口位置产生严重的流动分离，反导叶流场湍动能值随之上升，且其平均值随流量增大而递增，泵的水力效率明显下降。

[1]宇晓明,顾伯勤,邵春雷.叶轮切割形式对中比转数离心泵性能的影响[J].农业工程学报,2012,35(21):29-36.

[2]马新华,邵鑫,李浩,等.切割叶轮对离心泵性能影响的数值模拟分析[J].农机化研究,2013(8):217-220.

[3]李万军,刘德顺,金永平.高比转数双吸离心泵叶轮切割内部流场数值模拟[J].水电能源科学,2013,31(8):144-148.

[4]赵万勇,杨登峰,王磊,等.基于CFD的低比转数离心泵叶轮切割性能分析[J].西华大学学报：自然科学版,2013,32(2):37-41.

[5]汪家琼,孔繁余.多级离心泵叶轮与导叶水力性能优化研究[J].华中科技大学学报：自然科学版,2013,41(3):92-96.

[6]孔繁余,宿向辉,陈浩,等.离心泵径向导叶正叶片的优化设计[J].农业工程学报,2012,28(23):40-45.

[7]关醒凡.现代泵技术手册[M].北京:宇航出版社,1995：47-48.

[8]叶道星,汪洋.离心泵叶轮内部湍动能及耗散率分析[J].中国农村水利水电,2012(4):84-88.

[9]Li Wen-Guang. Impeller Trimming of an Industrial Centrifugal Viscous Oil Pump[J].Advanced Design and Manufacturing Techonlogy,2011,5(1):1-10.

[10]周孝华,刘厚林,王凯,等.HDMG型高压五级离心泵设计及数值模拟[J].水电能源科学,2013,31(9):182-185.

[11]Ukhin B V . Effect of Variation in the Diameter of a Centrifugal Dredge Impeller on Its Characteristics[J].Power Technology and Engineering,2007,41(1):8-13.

[12]王洋,刘洁琼.超比转数离心泵叶轮切割的三维流场数值模拟[J].农业工程机械学报,2012,43(5):79-83.

(编校：夏书林)

NumericalSimulationof3DFlowFieldforImpellerTrimoftheRadialDiffuserinaSingleStagetotheMulti-stagePump

YANG Cong-xin, FU you

(CollegeofEnergyandPowerEngineering，LanzhouUniv.ofTech.，Lanzhou730050China)

To investigate the influent of impeller trim on hydraulic performance of the radial diffuser in a centrifugal, the three-dimensional turbulent flow in a cut impeller of a single stage in multi-stage centrifugal pump MD-280-42×4 was numerically simulated using a SIMPLE algorithm based on Navier-Stokes equation, and the standard k-ε turbulence model. The external characteristic and the fluid flow of the radial diffuser in a centrifugal pump were analyzed. Research results show that with the size of impeller trimmed under the design conditions (Qd= 0.078 m3/s) increasing, The hydraulic efficiency and shaft power of the radial diffuser in a centrifugal decline. With the size of impeller trimming under the same small flow raising, the fluid flow of both gap between the impeller and the radial diffuser and the anti-guide becomes more and more uniform, and the hydraulic efficiency is enhanced in the same case; With the size of impeller trimming under the same mass flow increasing, the fluid flow of the guide vane and the anti-guide is badly interrupted, and the energy dissipation raises in the both positions. The hydraulic efficiency reduced in the same case.

impeller trim; radial diffuser; multistage centrifugal pump; anti-guide vane; numerical simulation

2014-07-10

杨从新(1964—)，男，教授，博导，主要研究方向为流体机械。

TH311

：A

：1673-159X(2015)03-0077-06

10.3969/j.issn.1673-159X.2015.03.016