“不变量思维法”解题应用浅析

云南省玉溪市峨山县教科所 靳翠德

数学问题，归根到底是量变问题．在高中数学复习迎考中，常常碰到所要解决的许多数学问题，在量与量的发生与发展变化过程中，有其“不变的量”，若能利用其规律和特征，作为问题分析与解决的思维主线，往往是我们解决数学问题的关键（或突破口）。

一、“值不变”

“值不变”指在数学量变过程中，某量（题设某种量或变化过程中产生的某种量）的值不变，或变化中的某量的某种特定值不变．

1．某种量的值不变

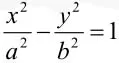
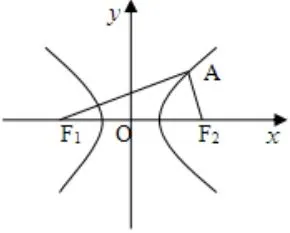
②正三棱柱ABC—A1B1C1的高为2，AB1与平面ABC所成角为450，则点C到平面ABC1的距离是＿．

分析：①按题意作如图所示：

∵

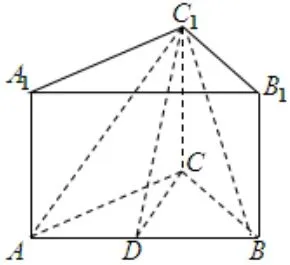
②如图，据题意得三棱锥—体积不变，即VC1−ABC=VC−ABC1，而与AB1平面ABC所成角为450，

∴AB=BB1=2，取AB的终点为D，则

【点评】①按双曲线的定义|AF1|−|AF2|，为双曲线的实轴长不变，利用勾股定理得解；②三棱锥C1−ABC休积不变，利用“体积换算”而得解．

2.变化的某种量的某值不变

例2（08年云南高中毕业生复习统测（一）9）在三棱锥V-ABC中，VA=BC，VB=AC，VC=AB，且三个侧面与底面ABC所成的二面角（锐角）分别为α , β,γ，则cosα + c os β +cos γ等于：

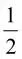
分析：满足题意的三棱锥是多变的，但侧面与底面所成角的余弦值之和是一个不变的确定值．而在变化的三棱锥中含正四面体这种特殊情形．所以可选择正四面体（特殊值法）来计算解决．如图：作正四面体V-ABC

设VO⊥面ABC，垂足为O，连接AO交BC于点D，连接VD，若侧面与底面所成角为θ，则θ=∠ADV．令正四面体的棱长为1，

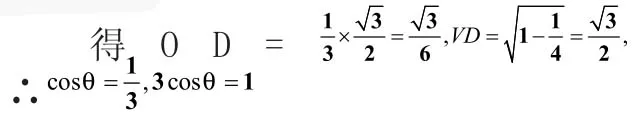
∴所求值为1，选（A）．

【点评】满足题意的三棱锥虽是多变的，但各侧面与底面所成角的余弦值之和这一特定值不变，因而选择符合条件的正四面体这种特殊情形来求解．这种思维方法为我们用特殊值法解选择题奠定基础．

二、“性不变”

“性不变”指在数学量变过程中，某量的特征性不变，可分为题设某变量的特征性不变或变化过程中产生的某种量的特征性不变两类．

1.题设某变量的特征性不变

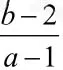
分析：无论实系数a、b怎样变化，方程x2+ax+ 2b=0的根，是开口向上的抛物线y=x2+ax+ 2b与x轴交点的横坐标这一特征性不变，而两根分别在（0，1）与（1，2）内．

作出点满足的可行域为l1:b= 0,l2:a+ 2b+ 1 = 0 ,l3:a+b+2 = 0

三线围成的区域（如图，不含边界）．

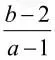
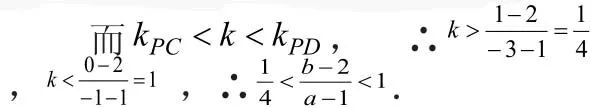
2.变化过程中产生的某种量的特征性不变

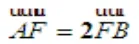
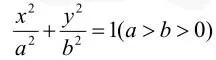
①4b4−4(a2+b2) (b2−a2b2)＞0，a2(b2+a2−1) ＞0，∴a2+b2＞ 1 (a＞b＞0)

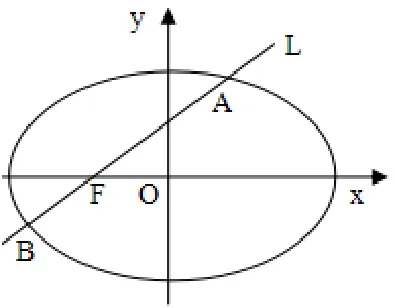
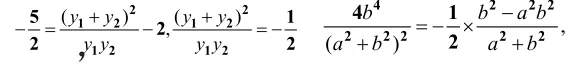
【点评】解决与相交弦有关的问题，往往利用交点坐标（X或Y坐标）是将直线方程代入曲线方程而得到的相应方程（X或Y的方程）的两根这一特征性，利用根与系数的关系而得解．

三、值与性均不变

应用“不变量思维法”解决数学问题时，始终紧紧抓住“变中的不变量”，利用其“特征性或值不变”作为思维主线，问题将会迎刃而解．有时这样的量同时具备“值与性”均不变的情况．

总之，“不变量思维法”在解题应用中思维十分活跃，无论是思维的形式、思维的广度和深度，都具有鲜明的特点及可适用性，进而引发诸如数学转换思想、分类讨论思想、数形结合思想、函数与方程思想以及选择题中特殊值思想方法等，都将体现其中．师生在复习迎考中，不妨一试，从中得益．