几类含参问题初探

吉林省白山市抚松县抚松五中 夏兴凤

含参问题是整个高中数学教学的重点，也是一个难点。高考中也少不了这类题型。面对某些含参问题，正面思考会觉得很困难。但通过转变思想，变换自变量，重新设定自变量的方法，会使解题思路凸现，而这个变化过程也大大优化了求解过程。下面是我平时在教学工作中对这一问题的一点思考，愿与我们大家共同分享。敬请斧正！

一、设定自变量求含参问题

例如：已知

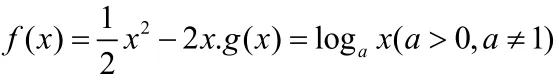
其中a为常数。

若h( x) = f( x) + g( x)是增函数，且h′( x)存在正零点（h′( x)为h(x)导数）

（1）求a值。

（ ⅰ ） 若0 ＜ a ＜ 1 ,ln a ＜0于 是x2⋅ln a − 2 x ⋅ ln a +1 ≤ 0恒 成 立 。 又h′( x)存在正零点，所以 ∆= 4 ln2a − 4 ln a =0。得ln a =0或ln a =1，与ln a ＜0矛盾。

（ ⅱ ） 若a＞1， 由x2⋅ln a − 2 x ⋅ ln a +1 ≥ 0恒成立，又h′( x)存在正零点，故∆=0，所以a =e。

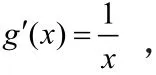
做到这里有的同学就不知该如何往下证明了，在上边这个式子中，出现了两个变量x1, x2，倘若把其中的一个设为自变量，另一个看做参变量，那么这个问题的思路便豁然开朗了。

不妨令X1=X，则令r( x) = x ⋅ ln x2−x ⋅ ln x − x2+x （0＜x＜x2）只需证r( x) ＜ 0，x ∈ (0,x2)即可。

r′( x) = l n x2− l n x ＞0

∵x ∈ (0,x2),∴ r′( x) ＞ 0∴r( x)在(0,x2)上 递 增 。 ∴ r ( x1) ＜ r( x2)即x1⋅ln x2−x1⋅ln x1−x2+x1＜0

二、变换自变量解含参问题

对于有些问题，如果把不等式看做关于 的不等式则解题过程非常复杂，但如果把不等式看做关于参数a的不等式则可简化解题过程，实现常量与变量的转化。

再如，对于满足的所有实数a，求使 不等式x2+ a x + 1 ＞ 2 x + a 恒成立的x的取值范围。

不等式化为(x − 1)a + (x −1)2＞0，令f( a ) = (x − 1 )a + (x −1)2，把它看作是关于a的一次函数，由有 −2 ≤ a ≤2，对于 −2 ≤ a ≤2时，要使f( a) ＞ 0恒 成 立 ， 只 需f( −2) = (x − 1 )(x −3) ＞ 0和f( 2) = (x − 1 )(x +1) ＞ 0同时成立即可，得x＜−1或x＞3。如此变换，复杂的问题就简单多了，学生做题时也省去了不必要的麻烦。

三、变更自变量从而回避讨论

某些分类讨论问题中含有多个变量，可根据题目的结构特点，选择某个变量为自变量，来个“反客为主”，从而回避讨论的繁琐。

例如：

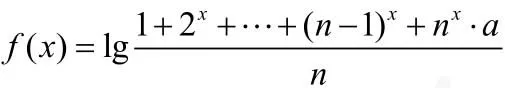
设，其中a ∈ R , n ∈ N 且n≥2当x∈ (− ∞,1]时f( x)有意义，求a的范围。

本题中有三个变量a, n, x 。这里条件复杂，解题方向不明确，如果选取其中的a 为自变量，把n, x 看作常量，问题就迎刃而解了。

由于n≥2且有x∈ (− ∞,1]，所以

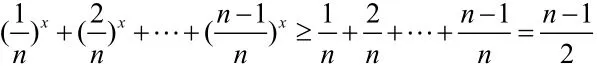
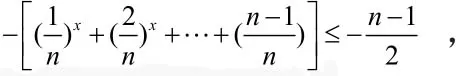
以上仅是我平时教学时的一些感触。其实，在教学过程中，还有许多问题值得我们总结和思考。很多平时我们觉得很难的问题，只要换种角度去看待，即利用转化的思想去分析研究，也许那些问题就不再深不可测了。当然这只是我个人的一点点想法，如有不当之处，敬请批评指正！