钢板喷丸处理残余应力场和表面粗糙度数值模拟
2015-07-16李亚东杨元录
强 斌, 李亚东, 顾 颖, 杨元录
(1.西南交通大学土木工程学院,四川 成都 610031;2.江苏中泰桥梁钢构股份有限公司,江苏 泰州 214521)
喷丸技术利用铸铁或陶瓷丸以一定的速度冲 击结构件,使其表面产生不均匀的塑性变形.喷丸技术被用来对桥梁用钢板进行表面处理,其功效主要体现在3个方面:一是可以对钢板表面进行除锈;二是使表面粗糙度达到涂装要求;三是喷丸会导致表层有限深度内产生残余压应力,有利于抑制疲劳裂纹的萌生和扩展,提高了结构件的使用寿命[1-3].
众多学者对喷丸技术进行了大量的研究.鉴于喷丸处理的试验研究非常耗时费力,相比之下大型商用有限元软件如ABAQUS、ANSYS等可以直观地展示整个动态喷丸过程,方便进行参数研究,因而得到了更多应用.
对喷丸过程的计算机模拟,已发展了多种模型.Hong等[4]建立了单丸有限元模型,分析了弹丸直径、冲击速度、入射角度和喷射次数对靶材表面残余应力的影响.Meo等[5]建立了单丸的轴对称模型,验证了喷丸处理产生的表面残余压应力可以有效削弱由于焊接导致的残余拉应力.然而,喷丸是一个非常复杂的过程,参与喷射的弹丸数量很多,简单的单丸模型存在一定的局限性.Meguid等[6]发展了单丸、双丸以及多丸三维模型,分析了单丸情况下弹丸尺寸、速度、形状对残余应力的影响,讨论了双丸弹丸间距对等效应力轨迹的作用以及靶材的应变硬化率对塑性区形成和分布的影响.Majzoobi等[7]模拟了多颗弹丸对靶材的冲击,获得了不同的弹丸速度和喷丸覆盖率对残余压应力的影响.Kim等[8]提出了面平均的方法,建立了多弹丸三维对称模型,系统地分析了喷丸残余应力的形成过程.Miao等[9]建立了随机的三维多丸模型,分析指出该模型在预测实际喷丸过程方面比传统的有限元模型更具合理性.
已有研究主要集中在对喷丸过程所产生的残余应力和塑性区域分布上,对表面粗糙度的关注及对于桥梁用钢的喷丸过程模拟较少,实际喷丸过程中的相关工艺参数依旧依靠试验和经验来确定.本文基于ABAQUS有限元软件建立三维多丸模型,对桥梁用钢的喷丸处理进行了数值模拟,分析了弹丸尺寸、喷射速度以及冲击次数对钢板表面残余压应力和表面粗糙度的影响;根据表面粗糙度Rz随冲击次数N的变化规律,建议采用对数函数来表示二者的关系,同时基于中国现行的公路和铁路桥梁涂装规范对表面粗糙度的要求,划定了弹丸直径为1.4 mm时对应的喷丸速度和冲击次数的合理范围,以此来指导实际工艺参数的选取.
1 有限元模型
1.1 多丸喷丸模型
有限元分析采用了ABAQUS/EXPLICIT有限元模块.文献[7,10]中都提到了常见的偏置建模法,借鉴该方法建立如图1所示的九弹丸(4+1+4)有限元模型,其中第一组4个弹丸彼此紧挨弹丸中心相距为D(D为弹丸直径),后续两组分别相对第一组弹丸在X-Y平面内以搭接率0.5向前后左右各偏置相应距离.这样建模是为了保证后续弹丸不再重复冲击前一位置,尽可能的冲击前一组未冲击到的盲点区域,从而提高喷丸覆盖率,九弹丸平面位置俯视图如图2所示.
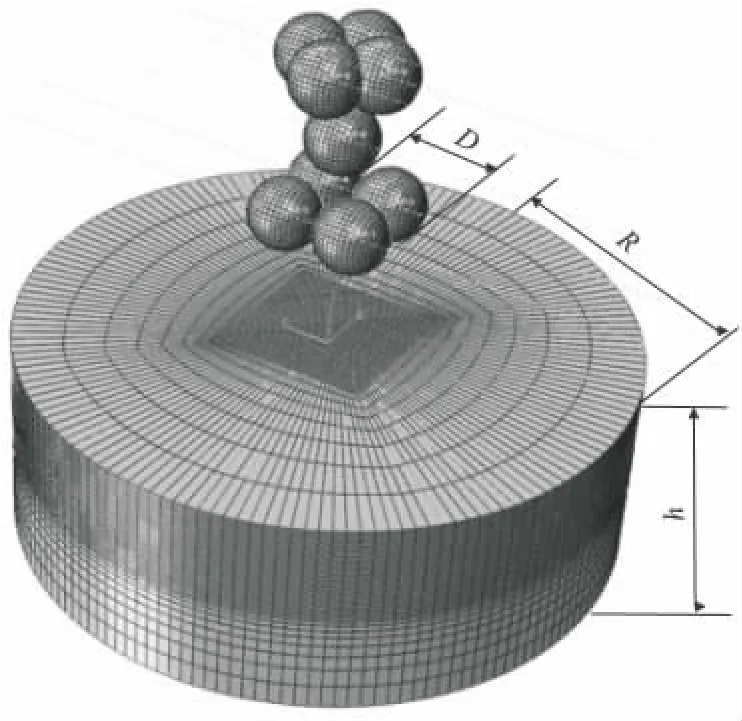
图1 多丸喷丸有限元模型Fig.1 The finite element model for multi-shot penning
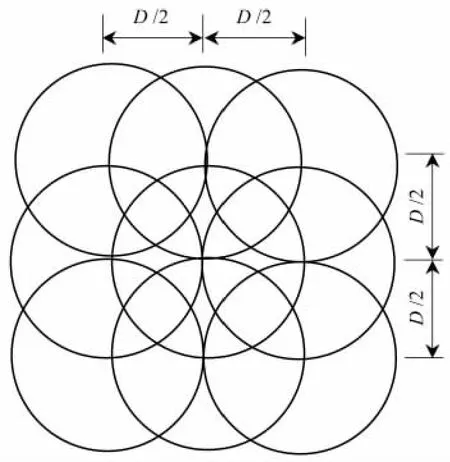
图2 弹丸位置俯视图Fig.2 The top view of shots location
图1中:圆柱体为靶材,球体为弹丸;R为圆形靶材的半径;h为靶材的板厚.9粒弹丸按冲击先后顺序分为3组(4+1+4),依次撞向9个不同的位置为完成1次冲击.模拟中选用了桥钢表面处理常用的5 种规格弹丸,分别为 D=1.0,1.2,1.4,1.7,2.0 mm,取 R=6 mm,h=5 mm >2D ,符合喷丸模型要求[11].为了提高计算精度,对弹丸与钢板表面接触区域以及厚度方向上进行了局部网格细化,最小单元尺寸为0.02D,弹丸单元尺寸与靶材细化区域单元尺寸相当.靶材面板采用三维实体单元C3D8R,弹丸采用三维实体单元C3D8.对靶材底面进行固定约束,弹丸只允许进行纵向(U3)运动,忽略了弹丸的反弹和相互碰撞.弹丸与面板的接触为面-面接触,考虑有限滑动,摩擦因数设为0.2,另外,考虑了几何非线性的影响.
为了验证文中有限元模型的合理性,与文献[12]的数值研究成果进行对比.利用本文所建立的模型,采用文献[12]中的相关参数模拟了弹丸速度为100 m/s时的单弹丸的喷丸过程,图3为当前模型模拟结果与文献[12]的对比,其中:σ11为水平向残余应力;σ0=600 MPa为文献[12]中靶材的屈服应力.由图3可知,两种模型的模拟结果非常接近,验证了本文所建立模型的合理性和准确性.
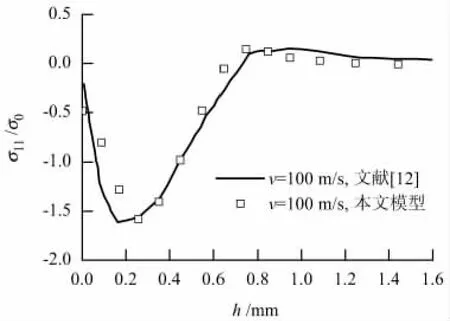
图3 有限元模型的数值验证Fig.3 Numerical validation of the finite element model
1.2 材料模型及参数
喷丸处理是动态冲击过程,涉及到材料的弹塑性变形,因而需选择合适的本构模型及约束条件.实际喷丸中采用的弹丸为硬度很高的铸铁丸,在模拟过程中将弹丸视为刚体.弹丸的材料参数为:弹性模量 E1=206 GPa;泊松比 ν1=0.3;密度 ρ1=7800 kg/m3.钢板靶材为 Q345钢,密度 ρ2=7800 kg/m3,弹性模量 E2=206 GPa,泊松比 ν2=0.3.喷丸过程中钢板表层会发生高速塑性变形,研究发现Q345钢有明显的应变率效应[13],因而本文中靶材钢板采用了可以反映出率相关硬化的Johnson-Cook(JC)动态本构模型,模型具体表达为
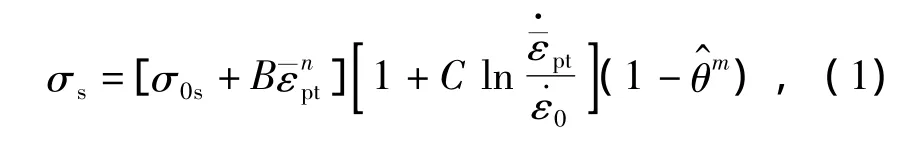
式中:
σs为各个应变率状态下的屈服应力;
σ0s为参考应变率和参考温度下的初始屈服应力[13],σ0s=374 MPa;
B、n分别为材料应变硬化模量和硬化指数[13],B=795.71279 MPa,n=0.4545;
C 为材料应变率强化参数[13],C=0.01586;
m为材料热软化指数;
JC动态本构模型将流动应力的变化分解为应变硬化f1(ε)、应变率强化f2()和热软化f3(θ)的乘积.
2 残余应力场分布模拟
高速运动的弹丸与靶材碰撞后,会使靶材表面发生永久塑性变形而形成凹坑和隆起,在靶材表面以及内部产生不均匀的残余应力场.本文分别研究了不同的冲击速度、冲击次数和弹丸直径对水平向残余应力(σ11)沿板厚h方向分布的影响.
2.1 冲击速度对残余应力的影响
取弹丸直径 D=1.4 mm,冲击速度 v=10,20,40,60,80,100 m/s.图 4 为冲击速度为 40 m/s,在9粒弹丸冲击1次后的水平向残余应力(σ11)分布云图.图4中:应力负表示受压;应力正表示受拉.
从图4可知,最大水平向残余压应力出现在后四粒弹丸冲击形成冲击坑表面正下方,最大拉应力位于冲击坑周围,中间位置的冲击坑由于受到周边冲击坑的挤压使得最大压应力减小.为了更好地反映出弹丸之间的相互影响,取中间冲击坑的中轴线作为残余应力沿厚度方向的研究路径,见图4(b).
图5给出了不同速度下9粒弹丸冲击1次后水平向残余应力(σ11)沿图4(b)所示路径的分布.
由图5(a)可知,当冲击速度分别为10、20 m/s时,因表面受冲击后形成的塑性凹坑较小,相邻凹坑间距较大,残余应力的变化趋势基本接近于单丸模型的结果[3].随着厚度的增加,残余压应力先增大到一个最大值而后逐渐减小直到转变成残余拉应力;残余拉应力先增大后减小,最终趋近于零.冲击速度较小时最大残余压应力随速度的增大而增大,出现的位置也向较深处发展.由于受到周边弹丸冲击的影响,多丸模型的残余压应力区域相应变大,对应的最大残余压应力值与单丸模型相差不大.
从图5(b)可知:当冲击速度大于20 m/s,喷丸覆盖率相应提高,相邻凹坑之间彼此相互影响,使得残余应力在初始阶段的压应力区出现了较明显的波动,而后残余压应力逐渐减小,此时较大的冲击速度所对应的残余压应力区也相应较大.
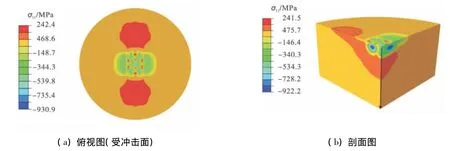
图4 冲击速度为40 m/s时残余应力云图Fig.4 Residual stress nephogram for impact velocity of 40 m/s

图5 不同冲击速度下残余应力沿厚度的分布Fig.5 Distribution of residual stress along the depth for different impact velocities
2.2 冲击次数对残余应力的影响
图6为弹丸直径D=1.4 mm,冲击速度分别为20、50 m/s时,9粒弹丸经过不同冲击次数后残余应力沿厚度的分布图.需要指出:多次冲击从第2次开始弹丸的冲击位置与第1次完全相同,分别按照(4+1+4)的顺序依次冲击第1次形成的凹坑位置.
由图6可知,当v=20 m/s时,残余压应力先增大后减小,随着冲击次数N的增加,最大残余压应力相应减小,出现的位置也逐渐向厚度方向发展;当v=50 m/s时,残余应力经历了先增大后减小再增大再减小的波动过程,随着冲击次数的增加,残余压应力在厚度方向的范围也越来越大.
对比图6(a)、(b)发现,当v=50 m/s时,经多次冲击后的最大残余压应力比v=20 m/s相应残余压应力小.其原因是,速度较大时,冲击坑面积比较大,喷丸覆盖率也随之提高,相邻的凹坑会互相影响,对残余应力有一个均匀化的过程,使得残余压应力在一定深度范围内的变化减小.
2.3 弹丸直径对残余应力的影响
图7 为 D=1.0,1.2,1.4,1.7,2.0 mm 时,9 粒弹丸冲击1次后残余应力沿厚度方向的分布,为了保证覆盖率,冲击速度取为50 m/s,此时的覆盖率接近100%.
由图7可知,残余应力在h=1.0 mm范围内经历了相似的波动过程,后逐渐变小;随着弹丸直径的变大,最大残余压应力值变化不明显,相应残余压应力在厚度方向的范围却越来越大.
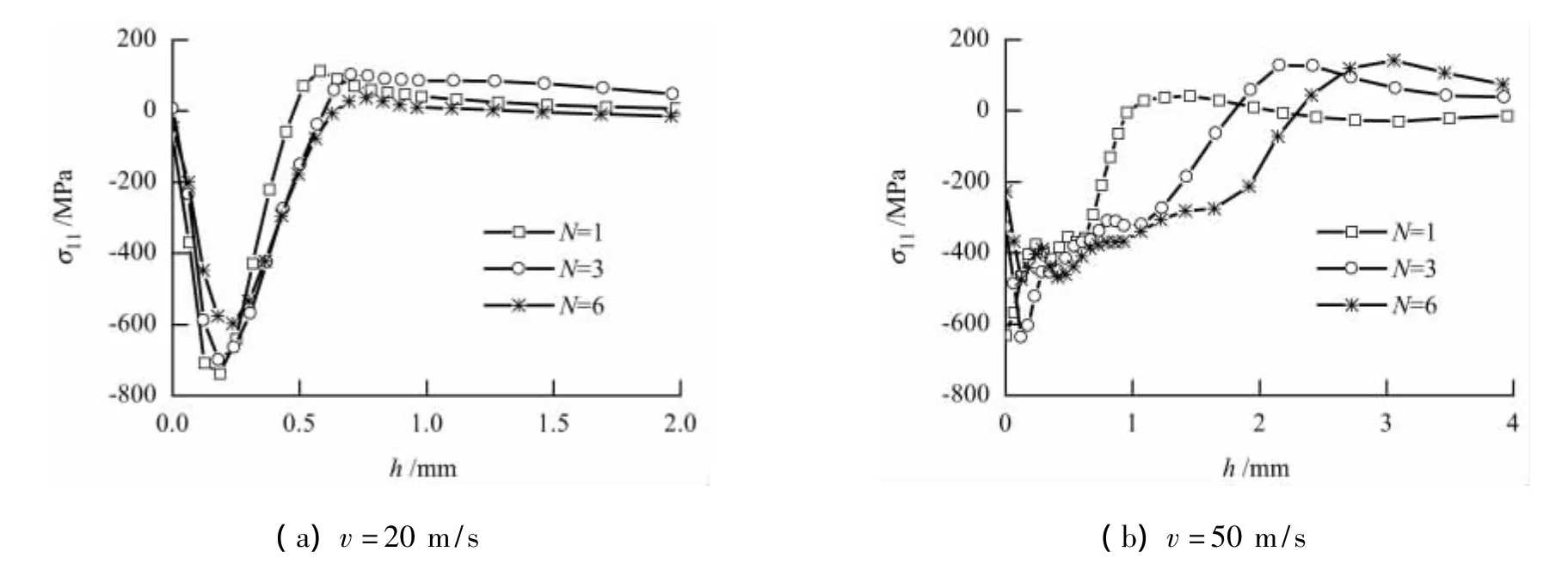
图6 不同冲击次数下残余应力沿厚度的分布Fig.6 Distribution of residual stress along the depth for different impact times
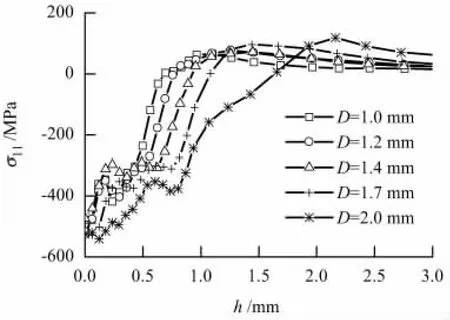
图7 不同弹丸直径下残余应力沿厚度的分布Fig.7 Distribution of residual stress along the depth for different shot diameters
3 表面粗糙度模拟
合理的防腐涂装要求钢板具有适当的表面粗糙度.现行的《铁路钢桥保护涂装及涂料供货技术条件》[14]中对于涂装前钢表面的粗糙度要求为:涂装涂料涂层时,钢表面粗糙度Rz(微观不平度十点高度)要求在25~50 μm之间;电弧喷涂铝金属时钢表面的粗糙度要求在50~100 μm之间.《公路桥梁钢结构防腐涂装技术条件》[15]中对于涂装前钢表面的粗糙度要求为:热喷锌(铝)时钢材表面粗糙度要求在60~100 μm之间,喷涂无机富锌底漆时钢材表面粗糙度为50~80 μm,喷涂其他防护层钢材表面粗糙度为30~75 μm.
Rz为评定粗糙度的参数,具体为取样长度内5个最大的轮廓峰高的平均值与5个最大的轮廓谷深的平均值之和.由于在模拟过程中喷射的弹丸大小和速度都相同,因而Rz取为中间冲击坑隆起高度和凹下深度之和,如图8所示,图中:h1和h2分别表示隆起高度和凹下深度,故有Rz=h1+h2.

图8 冲击坑示意图Fig.8 Schematic of impact crater
3.1 弹丸直径对表面粗糙度的影响
在相同的速度v=50 m/s时,弹丸取D=1.0,1.2,1.4,1.7,2.0 mm 进行喷丸模拟,图 9 给出了5种情况下9粒弹丸经过1次冲击后靶材表面凹坑的轮廓图,图中:H为冲击坑深度;x为距离冲击坑中心点的水平距离.
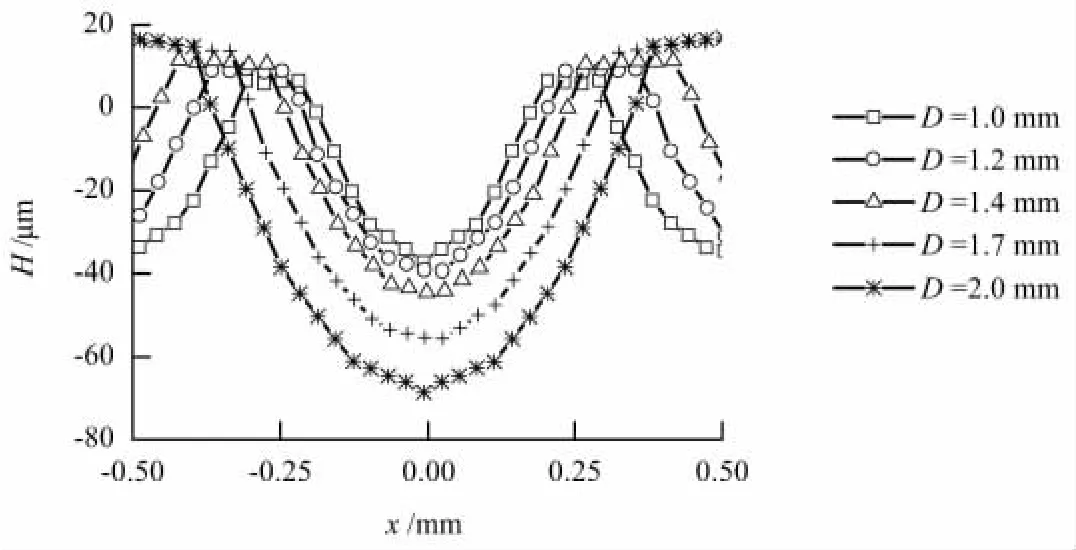
图9 不同弹丸直径下弹坑轮廓图Fig.9 Crater profiles for different shot diameters
由图9获得5种情况下的粗糙度Rz分别为44、48、56、72 和 86.随着弹丸直径的增大,弹丸所具有的动能也相应增大,使得靶材发生了较大的塑性变形,冲击坑面积和凹下深度也随之增大,冲击过后靶材表面粗糙度也增大.对隆起高度而言,前四种直径时的模拟结果随直径增大而相应增高,后两种直径时的结果比较接近,这是因为随着直径的逐渐增大,隆起高度受到相邻弹丸的挤压就更加明显,从而抑制了隆起高度持续增高.
3.2 冲击速度和次数对表面粗糙度的影响
采用偏置建模法建立的九弹丸模型保证了较高的喷丸覆盖率,同时也反映了随着时间增加弹丸对靶材的连续作用.因而借用九弹丸模型近似的评价弹丸冲击速度和次数对表面粗糙度的影响,预测粗糙度随二者的变化规律具有一定的现实意义和可行性.直径为1.4 mm的铸铁丸在实际喷丸过程中比较常用,据此取D=1.4 mm的弹丸模型,模拟了不同速度和不同冲击次数下的喷丸过程.
根据表面粗糙度Rz随冲击次数N的变化规律,建议采用对数函数表示二者的关系,表达式为

式中:a、b为待定常数,可以通过已有模拟数据进行拟合.
为了节约计算资源,针对8种不同的速度(10~80 m/s),分别模拟了9粒弹丸的6次冲击过程,然后利用模拟所得数据拟合出a和b的值,预测出后续多次冲击后的表面粗糙度值.图10给出了粗糙度Rz随冲击速度v、冲击次数N(N最大值取为20)变化的三维关系曲面.
由图10可知,在指定速度下,Rz随冲击次数的增加而增加,但增长率逐渐变小;当冲击次数一定时,Rz随速度的增加而增大.总之,粗糙度Rz随着冲击速度和冲击次数的增加而增大.
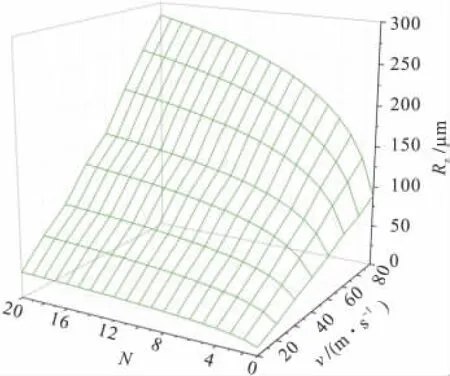
图10 不同冲击速度和冲击次数下表面粗糙度的分布Fig.10 Distribution of surface roughness for different impact velocities and impact times
根据现行铁路和公路涂装规范对于涂装前钢结构表面粗糙度Rz的要求,基于可用的喷丸工艺条件,可以从图10中选取设计粗糙度下对应的冲击次数和冲击速度的理想组合.例如:指定Rz=75 μm时,对应的组合可以是 v=30 m/s和 N=10,或者 v=40 m/s和 N=3.
4 结论
(1)当冲击速度较小时,残余压应力σ11沿厚度方向先增大后减小,整个变化趋势接近于单丸模型.当冲击速度大于20 m/s时,残余应力在初始阶段出现波动,而后逐渐减小归零.随着冲击速度、冲击次数以及弹丸直径的增加,残余压应力的分布范围逐渐向厚度方向发展,同时也使得表层残余应力场趋于均匀,缓解了应力集中.
(2)表面粗糙度Rz随着冲击速度、冲击次数和弹丸直径的增加而增大.在弹丸直径和冲击速度确定的前提下,基于本文提出的Rz-N关系曲线,可方便地组合出与设计粗糙度对应的冲击次数和冲击速度,以此来确定实际喷丸处理中的相应参数.
[1]王仁智.金属材料的喷丸强化原理及其强化机理综述[J].中国表面工程,2012,25(6):1-8.WANG Renzhi.Overview on the shot peening principle and its strengshening mechanisms for metallic materials[J]. China Surface Engineering, 2012,25(6):1-8.
[2]李雁淮,王飞,吕坚,等.单丸粒喷丸模型和多丸粒喷丸模型的有限元模拟[J].西安交通大学学报,2007,41(3):348-352.LI Yanhuai,WANG Fei,LÜ Jian,et al.Finite element analysis for shot-peening models of single shot impact and multiple impingement[J].Journal of Xi'an Jiaotong University,2007,41(3):348-352.
[3]凌祥,彭薇薇,倪红芳.喷丸三维残余应力场的有限元模拟[J].机械工程学报,2006,42(8):182-189.LING Xiang,PENG Weiwei,NI Hongfang.Simulation of 3D residual stress field of shot peening by dynamic finite element analysis[J]. Chinese Journal of Mechanical Engineering,2006,42(8):182-189.
[4]HONG T,OOI J Y,SHAW B.A numerical simulation to relate the shot peening parameters to the induced residual stresses[J]. Engineering Failure Analysis,2008,15:1097-1110.
[5]MEO M,VIGNJEVIC R.Finite element analysis of residual stress induced by shot peening process[J].Advances in Engineering Software,2003,34:569-575.
[6]MEGUID S A,SHAGAL G,STRANART J C J,et al.Three-dimensional dynamic finite element analysis of shot-peening induced residual stresses[J]. Finite Elements in Analysis and Design,1999,31:179-191.
[7]MAJZOOBI G H, AZIZIR, NIA A. A threedimensional simulation of shot peening process using multiple shot impacts[J]. Journal of Materials Processing Technology,2005,164/165:1226-1234.
[8]KIM T,LEE J H,LEE H,et al.An area-average approach to peening residual stress under multi-impacts using a three-dimensional symmetry-cell finite element model with plastic shots[J]. Materials and Design,2010,31:50-59.
[9]MIAO H Y,LAROSE S,PERRON C,et al.On the potential applications of a 3D random finite element model for the simulation of shot peening[J].Advances in Engineering Software,2009,40:1023-1038.
[10]张洪伟,陈家庆,张以都.基于多丸粒模型的喷丸表面强化过程数值模拟[J].塑性工程学报,2012,19(6):118-125.ZHANG Hongwei, CHEN Jiaqing, ZHANG Yidu.Numerical simulation of shot-peening process based on multiple shot model[J]. Journal of Plasticity Engineering,2012,19(6):118-125.
[11]MEGUID S A,SHAGAL G,STRANART J C.3D FE analysis peening of strain-rate sensitive materials using mul-tiple impingement model[J].International Journal of Impact Engineering,2002,27(2):119-134.
[12]MEGUID S A ,SHAGAL G,STRANART J C.Threedimensional dynamic finite element analysis of shotpeening induced residual stresses[J].Finite Elements in Analysis and Design,1999,31:179-191.
[13]于文静,史健勇,赵金城.Q345钢材动态力学性能研究[J].建筑结构,2011,41(3):28-30.YU Wenjing, SHI Jianyong, ZHAO Jincheng.Research of dynamic mechanical behavior of Q345 steel[J].Building Structure,2011,41(3):28-30.
[14]中华人民共和国铁道部.TB/T 1527—2011铁路钢桥保护涂装及涂料供货技术条件[S].北京:中国标准出版社,2011.
[15]中华人民共和国交通部.JT/T 722—2008公路桥梁钢结构防腐涂装技术条件[S].北京:中国标准出版社,2008.
