加载过程中钢筋混凝土梁弯曲变形的随机分析
2015-07-16徐腾飞白雪濛赵人达
徐腾飞, 白雪濛, 赵人达
(西南交通大学土木工程学院,四川 成都 610031)
随着高强材料的使用与结构断面日益轻薄化 的出现,正常使用极限状态对结构设计的影响作用日益增强[1].变形作为正常使用极限状态的重要指标之一,采用确定性分析方法很难得到与试验相吻合的结果[2].事实上,混凝土的力学特性存在随机性,这将导致钢筋混凝土梁的变形也具有随机特性,变形结果很难精确预测[3].在结构分析中,引入随机分析方法,有助于改善这一状况.
目前,对于混凝土结构的随机性研究,主要针对结构承载能力随机特性,而对于混凝土结构变形的随机特性研究较少[4].文献[5]分析了钢筋混凝土梁开裂后短期变形的随机特性,指出钢筋混凝土结构变形的变异系数为25% ~30%.A.Scanlon提出了基于概率的结构变形控制方法[6].文献[7]讨论了混凝土的不确定特性(包括:弹性模量、抗拉强度、时变效应等)对结构变形计算的影响.Bong-Seob Choi等利用蒙特卡洛法研究了给定荷载下钢筋混凝土梁变形的随机特性,该研究发现钢筋混凝土梁在不同的荷载下,变形的概率密度函数呈双峰或者单峰形态,概率密度函数形态与荷载、截面配筋率相关[2].
文献[8]假设钢筋混凝土梁的变形概率密度形态为正态或对数正态分布,考察了钢筋混凝土梁的正常使用极限状态的可靠度.文献[9]与文献[10]分别利用规范公式对钢筋混凝土梁与钢筋混凝土桥梁进行了正常使用极限状态可靠度分析.然而文献[8-10]均未研究钢筋混凝土梁变形的随机特性.
文献[11]利用响应面法结合蒙特卡洛抽样对钢筋混凝土柱的长期变形进行概率预测,发现当偏心受压柱最大应力接近混凝土抗拉强度时,抗拉强度对钢筋混凝土柱长期变形的随机性影响很大.文献[12]研究了最大名义拉应力接近混凝土抗拉强度时的钢筋混凝土梁的随机变形特性,并采用分片响应面的方法,解决了开裂非线性引起的钢筋混凝土梁刚度突变所导致的响应面不光滑问题.
以上关于钢筋混凝土梁变形随机性研究是基于给定荷载条件下的,而混凝土梁在服役期间,实际荷载是在正常使用荷载范围内变化的.在有明显差异的载荷条件下,不仅确定性的变形有较大的差异,同时其变形的随机特性也可能不同.因此,本文拟在以往研究的基础上,开展钢筋混凝土梁加载全过程变形的随机分析.以探求正常使用极限状态内钢筋混凝土梁变形的随机特性变化规律.
相比于其他材料,钢筋混凝土有其自身的特点.在正常使用荷载的范围内,普通钢筋混凝土结构通常处于开裂状态.混凝土截面开裂将引起截面刚度突变,势必影响其结构行为.因此,正常使用荷载下的钢筋混凝土结构变形随机分析必须考虑开裂引起的非线性效应.本文采用基于退化梁理论的钢筋混凝土非线性有限元方法,利用蒙特卡洛抽样技术,建立了钢筋混凝土梁的开裂非线性变形的随机分析模型.
1 钢筋混凝土结构非线性分析
本文采用钢筋混凝土非线性有限元分析软件CSBNLA进行钢筋混凝土结构开裂非线性的变形预测.退化梁单元的推导采用弱化的平截面假设,不再假定截面垂直于变形后梁轴线,以此反映剪切变形.退化梁单元既可以分析浅梁,也可分析深梁[13].
程序采用分块积分技术,能有效地考虑混凝土开裂等非线性结构行为.钢筋的应力-应变关系采用理想弹塑性模型,而混凝土材料特性采用一维的应力应变关系来描述[12-15],如图1所示.

图1 混凝土的应力-应变关系Fig.1 Stress-strain relationship for concrete
受压区混凝土应力-应变(σ-ε)关系描述为
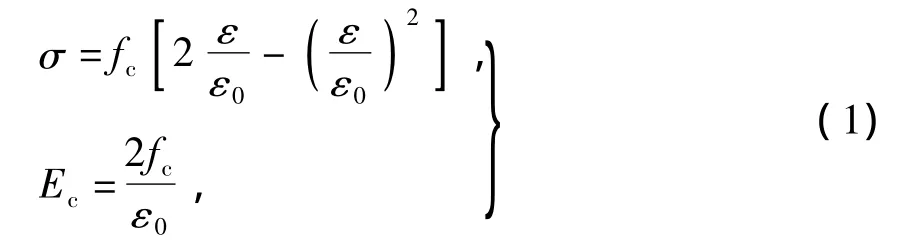
式中:Ec为混凝土材料的初始弹性模量;
fc为混凝土单轴抗压强度峰值.
在考虑拉伸刚化效应的前提下,受拉区的应力-应变关系为
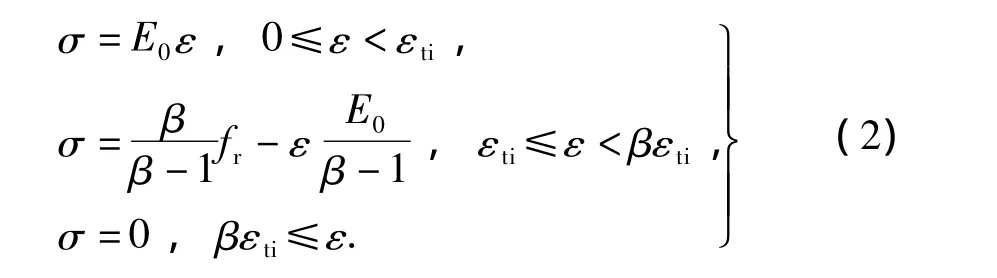
2 随机分析模型
本文拟采用Bresler经典试验梁为分析对象.考虑的随机源包括:混凝土的抗压强度fc,混凝土的弹性模量Ec,混凝土的抗拉强度fr,拉伸刚化模型 β,钢筋弹性模量 Es,屈服强度 fy,外观尺寸 b、h0,施加荷载F.
表1给出了各随机变量的随机特性,其中fcm为抗压强度均值,Esm为钢筋弹性模量均值,fym为钢筋屈服强度均值,bm为截面宽度均值,h0m为截面有效高度均值,Fm为施加荷载均值.
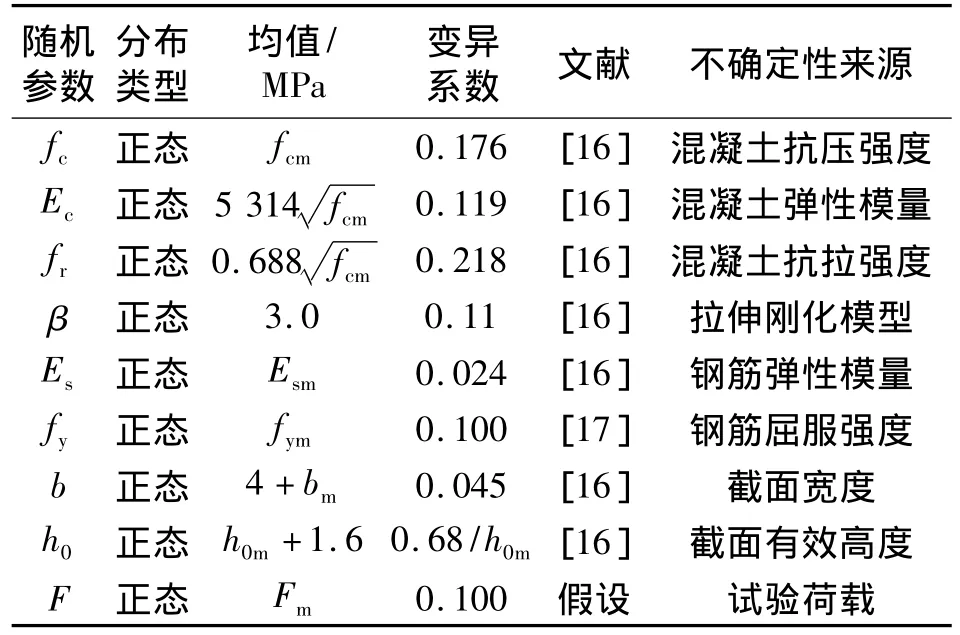
表1 随机变量的随机特性Tab.1 Statistical properties of random variables
本文采用蒙特卡洛抽样的方法进行钢筋混凝土梁受力全过程随机分析,每次加载的非线性分析次数为10000次.由于蒙特卡洛法需进行大量的非线性计算,为提高计算效率,故采用并行算法在高级计算工作站上完成.
3 钢筋混凝土梁变形随机分析
3.1 模型介绍
1963年Bresler与Scordelis教授完成了一组钢筋混凝土简支梁加载试验.这批试验梁被认为是经典试验梁,并被大量的钢筋混凝土有限元分析模型作为校核依据[17-19].
试验梁为矩形断面,尺寸及钢筋位置如图2所示.
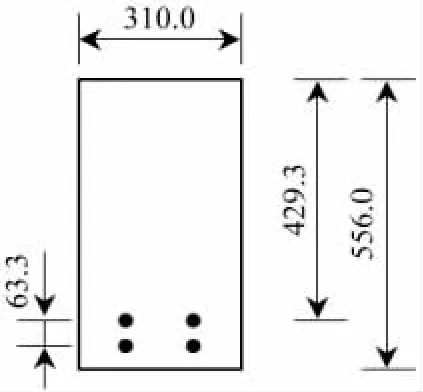
图2 试验梁断面尺寸Fig.2 Sizes of beam cross section
混凝土抗压强度为22.6 MPa,抗拉强度为3.97 MPa;钢筋的抗拉强度为555 MPa,极限强度为933 MPa,弹性模量为218 GPa.受拉钢筋单根面积为645 mm2.
试验梁为简支梁,跨度为3.66 m.采用跨中单点加载,试验结果表明极限承载力Fu为334 kN.本文拟分析正常使用荷载下梁体变形的随机特性,故最大荷载取为216 kN.
3.2 加载过程梁体变形的随机特性
图3给出了跨中位置加载全过程荷载位移曲线的试验值、随机分析均值以及随机分析的2.28%与 97.72%分位数值.由图3可以看出,试验值落在2.28% ~97.72%的概率区间内,且与随机分析的均值曲线比较吻合,这也证明了本文随机分析模型的正确性.
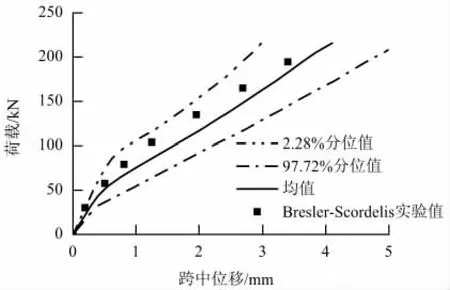
图3 试验梁跨中荷载位移曲线Fig.3 Load vs deflection at half span of test beam
考虑到钢筋混凝土加载过程中概率分布形态在发生变化,故利用概率区间定义离散系数

式中:
Δu为跨中变形的97.72%分位值;
Δs为跨中变形的2.28%分位值;
Δmean为跨中变形均值.
当变形响应为正态分布时,离散系数λ退化为σ/Δmean,即传统的变异系数.
图4给出了加载过程中,跨中位移的离散系数变化规律,同时也给出了开裂荷载的概率密度曲线以及开裂荷载的均值 Fcr,mean、2.28% 分位数值Fcr,s与 97.72% 分位数值 Fcr,u.由图 4 可以看出,在加载过程中,跨中位移的离散系数呈先增大后减小,最终趋于稳定的趋势.而离散系数出现峰值的区间恰好与开裂荷载高概率区间吻合.
选择A点(加载起点)、B点(开裂荷载均值)与C点(加载终点)绘制3个点对应荷载下跨中变形的概率密度曲线,如图5所示.
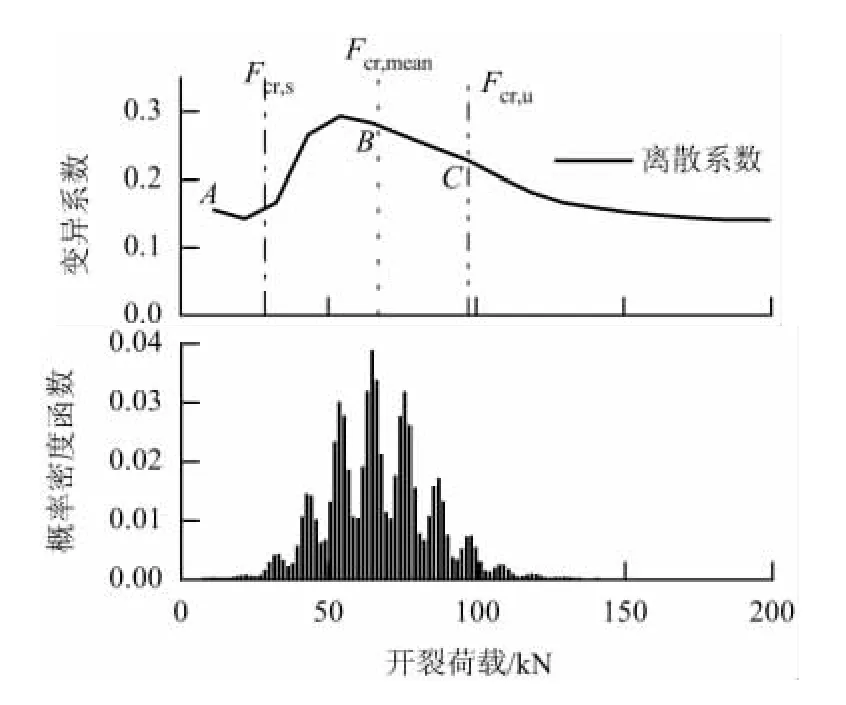
图4 跨中变形的离散系数与开裂荷载的概率密度曲线Fig.4 Coefficient of variability of deflection at half span and probability density of cracking load
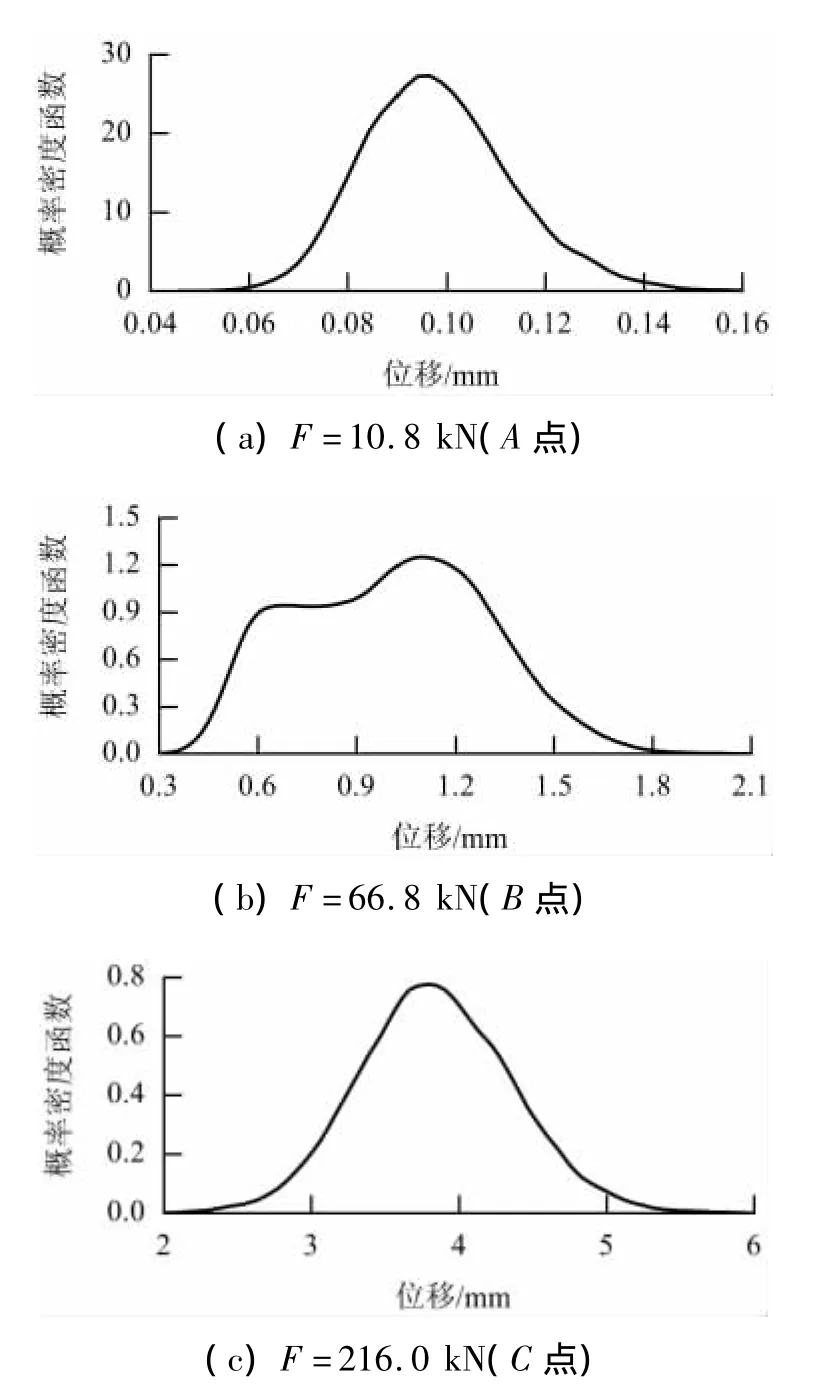
图5 跨中变形的概率密度曲线Fig.5 Probability density of deflection at half span
由图5可以看出,在A点与C点,跨中挠度的概率密度曲线呈现单峰形态,类似正态分布,而在B点(开裂荷载均值),跨中挠度的概率密度曲线呈现出典型的双峰分布形态.当梁体所受荷载在开裂荷载的高概率区间内时,由于材料参数的随机性,梁体的实际开裂荷载为随机变量,故梁体截面开裂与不开裂的几率相当.而混凝土截面开裂前后刚度差异较大,对应的梁体变形也有很大不同,梁体变形的概率密度曲线呈双峰形态,变异性大.
3.3 参数分析
配筋率是钢筋混凝土梁的重要性能指标,其不仅影响钢筋混凝土梁的极限承载能力,也影响钢筋混凝土梁开裂后的刚度,从而影响梁体的变形.
荷载加到216 kN前,不同配筋率梁体的跨中截面荷载与位移均值曲线如图6所示.由图中可以看出,不同配筋率下,开裂前的变形曲线基本一致,但开裂后由于配筋率不同,导致开裂程度的差异,荷载位移曲线差异很大.
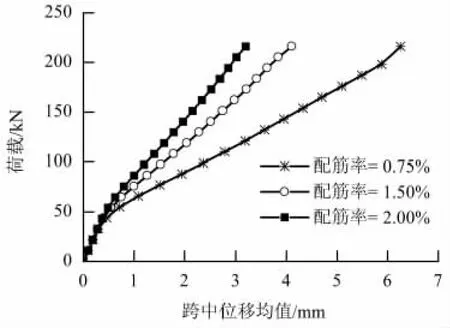
图6 不同配筋率下跨中挠度均值曲线Fig.6 Mean value of deflection at half span with different steel ratios reinforcement ratios
图7所示为配筋率分别为0.75%(最小配筋率)、1.50%(试验梁)与 2.00%(最大配筋率)时,跨中变形的离散系数随荷载的变化关系曲线.
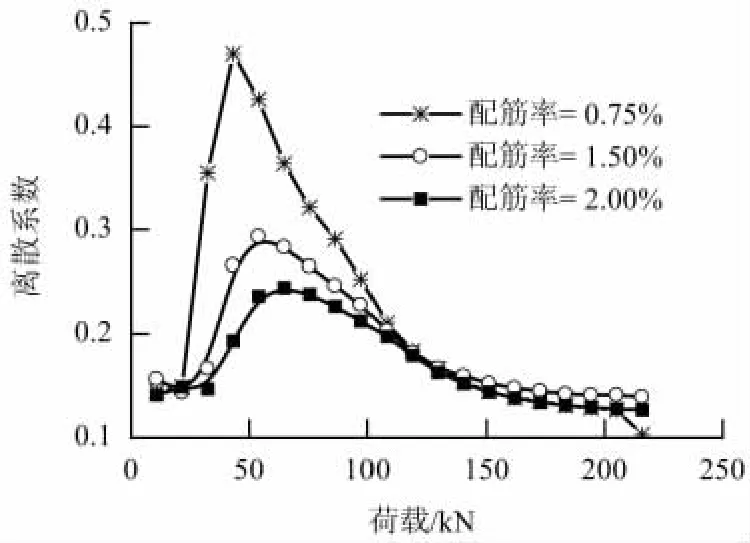
图7 不同配筋率下跨中挠度变形的离散系数Fig.7 Coefficient of variability of deflection at half span in loading process with different reinforcement ratios
从图7可以看出,不同配筋率的钢筋混凝土梁跨中挠度离散系数峰值出现位置基本相同,但峰值大小有明显差异,配筋率与峰值成反比例关系.随着荷载的增大,不同配筋率的钢筋混凝土梁跨中挠度的离散系数差异迅速减小,最终趋于一致.
由3.2节分析可知,离散系数增大是截面开裂的随机性引起的,而离散系数出现峰值的位置对应着截面开裂荷载的高概率区间.不同配筋率的混凝土截面开裂荷载基本一致,故不同配筋率的钢筋混凝土梁跨中挠度峰值位置也基本一致.在截面开裂的瞬间,受拉开裂混凝土原本承担的荷载全部转化到钢筋承担,钢筋的应力与变形均迅速增大,配筋率越低,增大幅度越大.因此配筋率越低,跨中挠度离散系数峰值越大.
由表1中数据可以看出,构成钢筋混凝土梁变形随机性的各个不确定性因素中,混凝土材料的离散性远大于钢筋材料的离散性.随着荷载的增大,混凝土逐渐退出工作,混凝土对结构变形的影响逐渐减小.故跨中挠度的变异性逐渐减小,最终趋于一致.
4 结论
本文对钢筋混凝土试验梁加载全过程的变形概率特性展开研究,结果表明:
(1)本文随机分析模型计算的荷载位移曲线均值与经典试验结果吻合较好,试验点均落在本文给出的概率区间内,证明了本文分析模型的正确性.
(2)钢筋混凝土梁在加载过程中,变形的变异性并非恒定不变的.当荷载位于开裂荷载高概率区间时,梁体变形的变异性迅速增大并达到峰值.随着荷载的增大,梁体变形的变异性开始减小,最终保持不变.由于加载过程中位移变异性的变化,当计算混凝土结构正常使用极限状态可靠度时,临界状态的可靠度指标可能不是加载过程中最低的可靠度指标.
(3)不同配筋率的钢筋混凝土梁开裂后变形的均值有明显差异.而变形的变异性主要出现在开裂荷载的高概率区间内.此时,配筋率越低,变异性越大.随着荷载的增大,梁体变形的变异性反而趋于一致.
[1]Bljuger Ephraim. Models ofR.C structures for probabilistic serviceability analysis[J].Computer and Structures,1998,67:19-27.
[2]CHOI B S,SCANLON A,JOHNSON P A.Monte Carlo simulation of immediate and time-dependent deflections ofreinforced concrete beamsand slabs[J]. ACI Structural Journal,2004,101(5):633-641.
[3]KIM J J,TAHA M M R,NOH H C,et al.Reliability analysis to resolve difficulty in choosing from alternative deflection models of RC beams[J].Mechanical Systems and Signal Processing,2013,37(1):240-252.
[4]KHOR E H,ROSOWSKY D V,STEWART M G.Probabilistic analysis of time-dependent deflections of RC flexural members[J]. Computer and Structures,2001,79(16):1461-1472.
[5]RAMSAY R J,MIRZA S A,MACGREGOR J G.Monte Carlo study of short time deflections of reinforced concrete beams[J].ACI Journal Proceedings,1979,79(8):897-918.
[6]SCANLON A,PINHEIRO L.Allowable deflections:The other side of the equation[J].ACI SP,1992,133:111-120.
[7]TAHA M M R,HASSANAIN M A.Estimating the error in calculated deflections of HPC slabs:a parametric study using the theory of error propagation[J].ACI SP,2003,210:65-92.
[8]唐铁羽,赵国藩.钢筋混凝土结构正常使用极限状态可靠性分析[C]∥第六届全国结构工程学术会议论文集:第2卷.广州:[s.n.],1997:98-108.
[9]赵羽习,金伟良.正常使用极限状态下混凝土结构构件可靠度的分析方法[J].浙江大学学报,2002,36(6):674-679.ZHAO Yuxi,JIN Weiliang.Methods of reliability based on serviceability limited state for concrete structural members[J].Journal of Zhejiang University,2002,36(6):674-679.
[10]孙晓燕,黄乘逵.既有钢筋混凝土桥梁正常使用极限状态可靠度分析[J].湖南大学学报,2006,33(4):21-25.SUN Xiaoyan, HUANG Chengkui. Methodsof reliability analysis based on serviceability limited state for existing reinforced concrete bridges[J].Journal of Hunan University,2006,33(4):21-25.
[11]徐腾飞,向天宇,赵人达.偏心钢筋混凝土受压柱长期变形分析[J].西南交通大学学报,2014,49(4):626-630.XU Tengfei,XIANG Tianyu,ZHAO Renda.Longterm random deflection of eccentrically loaded RC column[J].Journal of Southwest Jiaotong University,2014,49(4):626-630.
[12]徐腾飞,向天宇,白雪濛,等.基于分片响应面的钢筋混凝土梁变形随机模拟[J].工程力学,2014,31(11):170-174.XU Tengfei,XIANG Tianyu,BAI Xuemeng,et al.Stochastic simulation of reinforced concrete beams with a piecewise response surface[J].Engineering Mechanics,2014,31(11):170-174.
[13]童育强,向天宇,赵人达.基于退化理论的空间梁单元有限元分析[J].工程力学,2006,23(1):33-37.TONG Yuqiang,XIANG Tianyu,ZHAO Renda.A degenerated 3D beam elementforfinite element analysis[J].Engineering Mechanics,2006,23(1):33-37.
[14]马坤,向天宇,赵人达,等.高速铁路钢筋混凝土拱桥长期变形的随机分析[J].土木工程学报,2012,45(11):141-146.MA Kun, XIANG Tianyu, ZHAO Renda, et al.Stochastic analysis of long-term deformation of reinforced concrete arch bridges for high-speed railways[J].China Civil Engineering Journal,2012,45(11):141-146.
[15]刘蕾蕾,白雪濛,徐腾飞,钢筋混凝土梁时变变形的概率密度演化[C]∥第23届全国结构工程学术会议论文集:第Ⅱ册.兰州:[s.n.],2014:80-86.
[16]VAL D V,CHERNIN L.Serviceability reliability of reinforced concrete beams with corroded reinforcement[J].Journal of Structural Engineering.2009,19(3):896-905.
[17]GOEL R,KUMAR R,PAUL D K.Comparative study of various creep and shrinkage prediction models for concrete[J].Journal of Materials in Civil Engineering.2007,19(3):249-260.
[18]BRESLER B,SCORDELIS A C.Shear strength of reinforced concrete beams[J]. Journal Proceedings.1963,60(1):51-72.
[19]VECCHIO F J,SHIM W.Experimental and analytical reexamination of classic concrete beam test[J].Journal of Structural Engineering,2004,130(3):460-469.
