动车组单部件两级非完美维护策略及优化研究
2015-07-16杜维鑫刘志龙蒋祖华
王 红, 杜维鑫, 刘志龙, 蒋祖华
(1.兰州交通大学机电工程学院,甘肃 兰州 730070;2.上海交通大学机械与动力工程学院,上海 200240)
国内外一直使用多级维护机制对高速动车组进行维护[1].维护等级越高,维护时所涉及部件的零件就越多,进而部件恢复的程度就越好,直到在某一级维护时对部件进行更换.在这种机制中,对部件进行更换之前的各级维护对部件来说都属于非完美维护,由于每种级别中维护零件的范围不同,这就使得各个非完美维护之间又存在一定的差异,属于“多级别非完美维护”.且由于动车组部件价格昂贵,更换费时费力,在实际操作中对部件的整体更换很少发生,而是采取多级别非完美维护的手段,使其服役时间尽量延长.
然而,在以往非完美维护问题的研究中,一类是对一级非完美维护进行研究[2-3],另一类虽然对预防性维护的种类有所划分,但还是从是否为完美维护这个角度将其划分为更换和维修两种形式.文献[4-7]以可修复的劣化系统为研究对象,将预防性维护方式设定为维修和更换,对系统的维修策略进行优化.文献[8-9]中预防性维修方式增加了保养,但是由于其对系统可靠度的影响较小,没有作为维护决策的研究重点.这些维护模型为生产系统的维护决策提供了有力支持,但是由于动车组维护机制的特殊性,采用这些模型对动车组部件的维护计划进行研究是不够准确的.此外,目前已有的维修模式对检测、诊断条件和人员素质的要求高,前期投资大[10],致使其很难在部件维护中广泛应用.
因此,本文选取在动车组四级修时进行更换的某部件为研究对象,以成熟的可靠性理论为根据,建立了单部件的两级非完美预防性维护模型,即初级维修和高级维修.为了使部件的维护策略与我国动车组维护制度贴合更加紧密,提出了两种更具操作性的动车组部件维护方案,并在保证部件安全运营的前提下,对部件的维护费用和维护时间进行了优化.
1 问题描述与假设
动车组某部件要求在整车的四级检修(里程为Lmax)时进行更换,部件运行允许的最小可靠度为Rmin.在里程区间[0,Lmax]内的单部件预防性维护方式只有维修,且方式为“维护非新”,但在维护时对维修的选择有初级维修和高级维修两种形式.
根据我国动车组各级检修的检修范围和性质,对要求在动车组四级修修程时进行更换的部件维护效果做如下处理.我国动车组的维修统一划分为一至五级修:一级修是以快速检查为主的例行检修,其目的是维持列车部件处于正常工作状态,发现并尽早消除安全隐患,对部件来说其相当于小修;二级修以部件专项修为主要内容,对部件施行专业化检修,但由于检修场所能力的限制,对部件的修理程度有限,相当于对部件的一种非完美维护(初级维修);三至五级修的维修场所为动车基地或主机厂,高一级别维修的检修范围和程度在低一级的基础上都有所增加,维修和更换的对象也由零件扩大到部件,直至在五级修中对整车进行分解检修.本文中该部件在四级修时进行更换,因此,在五级修修程时也对部件进行更换,在三级修时对部件施行高于二级修时的非完美维护(高级维修).
结合我国动车组的维护制度,提出动车组部件的两种维护方案:方案1,选择部件所属动车组的检修时机对部件进行维护,对部件维修的级别不做要求;方案2,部件的检修时机和维修级别都必须与动车组检修一致,如图1所示.
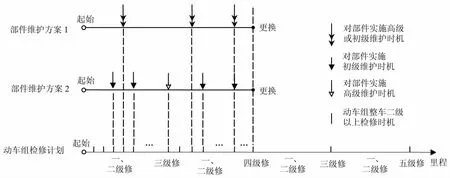
图1 结合动车组检修计划为部件提出的两种维护方案Fig.1 Two maintenance plans for component combined with the EMU's maintenance rule
为此,本文以部件在服役里程内的总维修费用最低、总维修时间最少为预防性维修计划的优化目标,并且使部件满足最低的可靠度要求.针对本文要解决的问题,作以下假设:
(1)部件从全新状态开始工作;
(2)部件有单次最小维修操作时间;
(3)部件的故障里程服从尺寸参数为η,形状参数为β(β>1)的威布尔分布.有研究表明,威布尔分布被称为“万能分布”[11],通过对其参数的设定可以描述研究对象的多种故障率分布形式,如指数分布、对数正态分布、威布尔分布等[12];
(4)小修用来消除部件产生意外故障的可能性,使部件处于正常运行状态.小修不改变部件的可靠度和衰减速率;
(5)不同等级的维修对未失效零件的改善效果相同;
(6)部件的检修时机必须与所属动车组的检修时机相一致,且在任何情况下对部件的维护操作时间小于对整车的维护操作时间;
(7)整车的三级检修可以对部件进行初级维修,而二级检修不可以对部件进行高级维修.
2 模型的建立
2.1 可靠度建模
部件在运行里程范围[l0,lm]内共进行了m-1次预防性维修,并且在lm时对部件进行整体更换,维护的时机分别为li(i=1,2,…,m),其中 l0=0,lm=Lmax.从li-1到li之间的区间称为部件的第 i个维护周期,用R[i](l)表示该周期内的部件可靠度函数.
参照文献[8-9]中的可靠度模型,第i个预防性维修周期部件的可靠度函数表示为
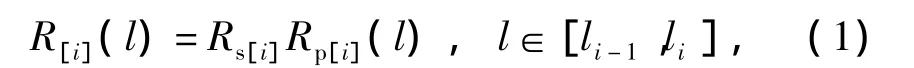
式中:Rs[i]为第i个预防性维修周期失效零件的初始可靠度;
Rp[i](l)为第i个预防性维修周期内未失效零件在运营里程为l时的可靠度,i=1,2,…,m.
由于非完美维护的等级不同,维修后可靠度会在恢复程度以及可靠度衰减加速程度这两个方面有所差异,如图2所示.
2.1.1 可靠度恢复程度建模
考虑“维护非新”的维护方式,引入可靠度修复因子θ1(0<θ1<1).本文研究的问题中,部件的维护方式有初级维修和高级维修,因此提出变量

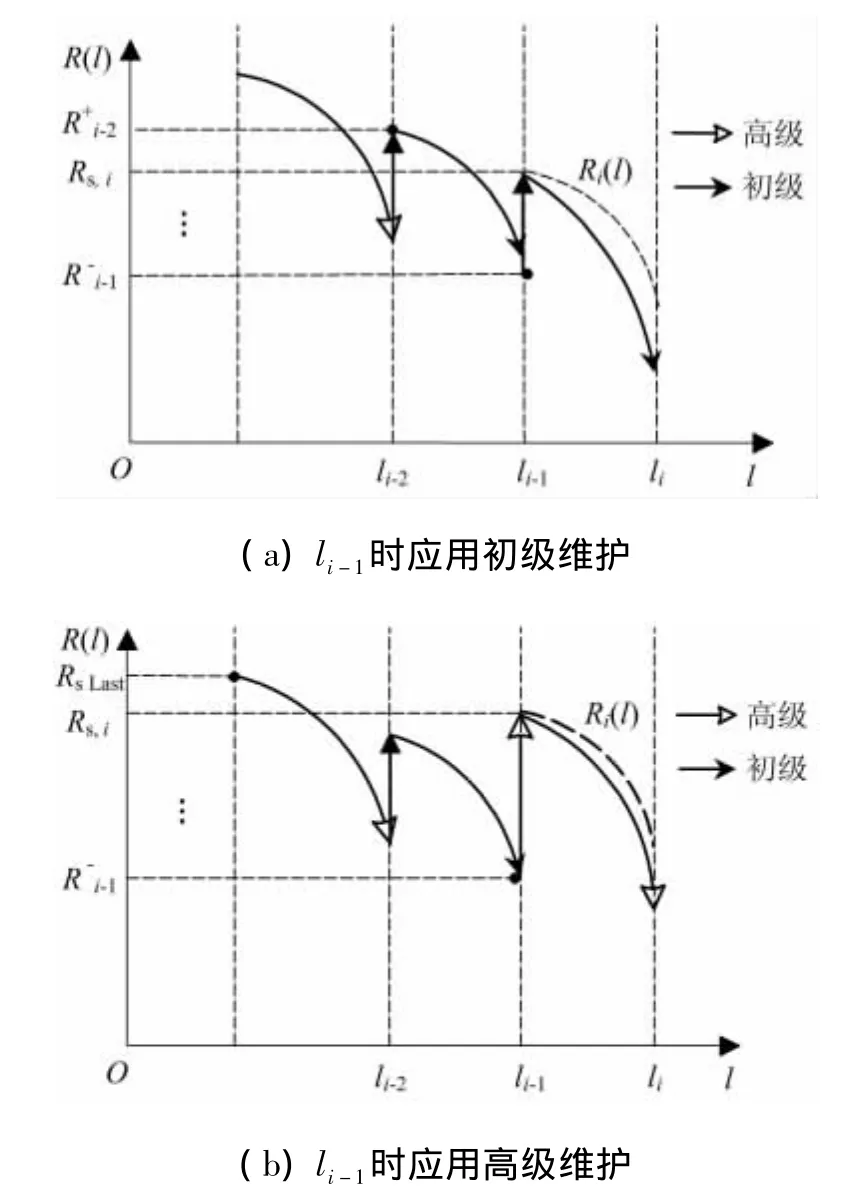
图2 不同维修类型下可靠度的变化情况Fig.2 Variation of reliability on different maintenance actions
由图2可见,在li-1时对部件进行第i-1次预防性维护,若执行初级维修,则恢复后的可靠度小于上一次维护后部件的可靠度R+i-2;若执行高级维修,则恢复后的可靠度小于上一次高级维护后部件的可靠度RsLast.可靠度恢复程度的定量关系为
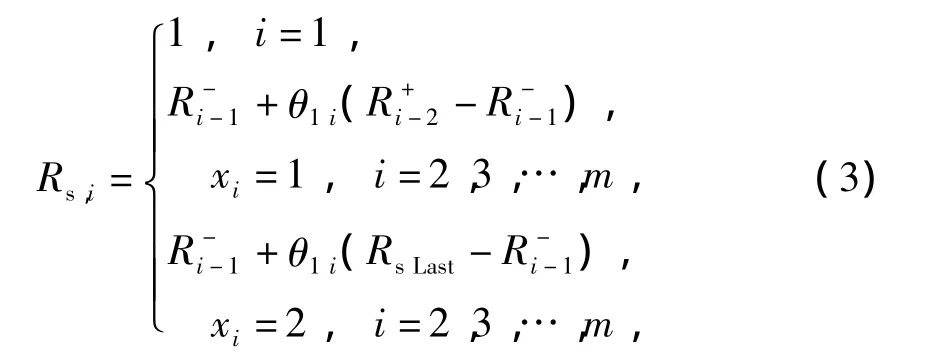
式中:
θ1i=(2 - xi-1)θ1j+(xi-1- 1)θ1s为第 i个维护周期的可靠度修复因子;
θ1j与θ1s为初级维护和高级维护的可靠度修复因子;
Ri-表示第i次预防性维修前后的部件可靠度;
RsLast为上次高级维护后部件的可靠度恢复值.
2.1.2 可靠度衰减速度建模
如图2所示,第i个预防性维护周期内部件的可靠度衰减速率会在第i-1个周期的基础上有所增加.由于li-1时对部件执行维修的等级不同,维护后部件的可靠度衰退速率的加速情况会有所区别,初级维修后衰退速率加速的较多,而高级维修后衰退速率加速的较少.
己知部件的故障里程服从威布尔分布,则第i个预防性维修周期内的可靠度函数为
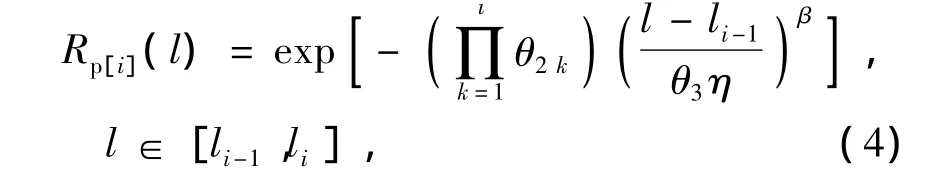
式中:
θ2i为第i个维护周期的可靠度加速因子,θ2i≥1;
θ3为未故障相关零件改善因子,0<θ3<1.
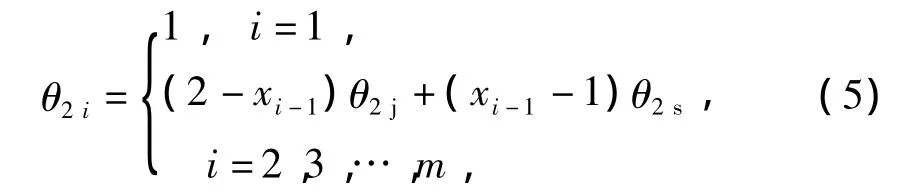
式中:θ2j、θ2s分别为初级维修和高级维修的可靠度加速因子,且1 < θ2s< θ2j.
综上所述,第i个预防性维修周期内部件的可靠度表示为
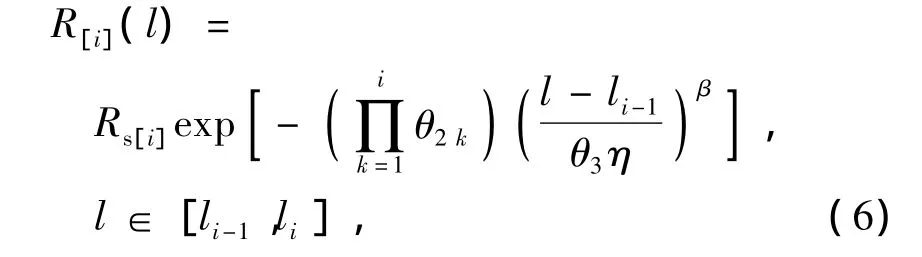
式中:
i=1,2,…,m.
可靠度与故障率之间的关系为
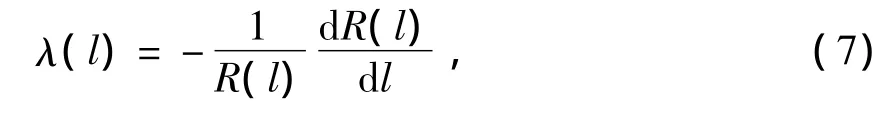
将式(6)代入(7),得出在第i个维护周期内部件的故障率
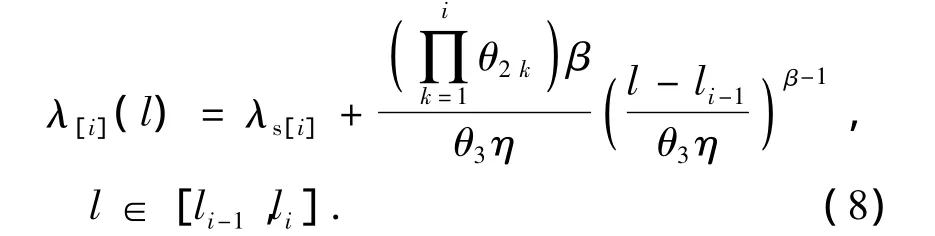
部件第i个预防性维修周期的初始故障率
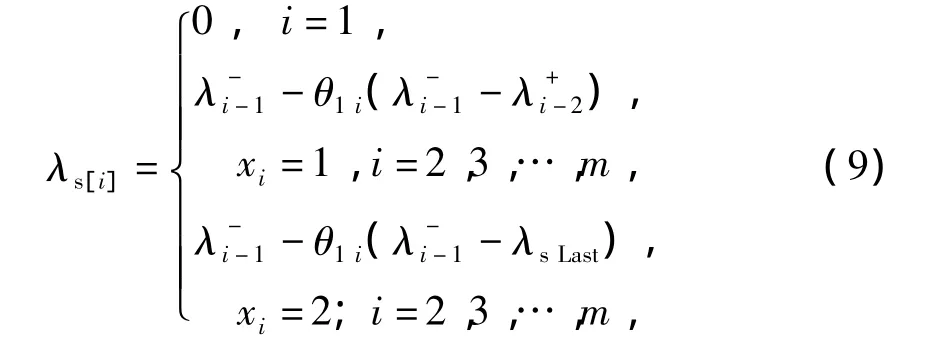
式中:
λsLast为上次高级维护后部件的故障率恢复值.
2.2 维护时间建模
部件一个更换周期内的总维护时间为
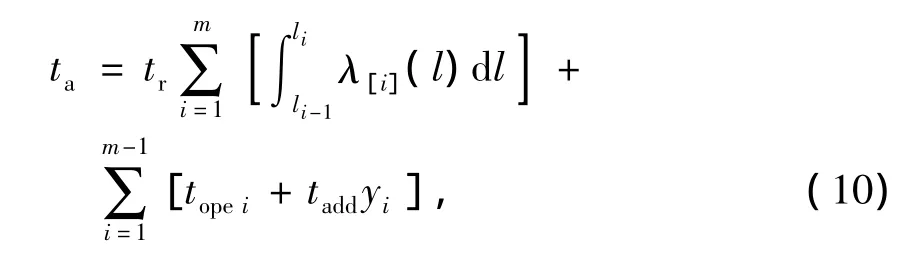
式中:tr为部件小修的维修时间;
topei为第i次预防性维修操作时间;
tadd为整车的维护级别无法满足部件的维修要求时,部件在运输过程中产生的附加时间;
yi用来表示第i次预防性维修时部件的维修级别和整车维修级别的匹配情况:

部件处于不同可靠度时对其进行维护所需的操作时间不同,本文用不可靠度(F=1-R)对维护操作时间进行建模.随着不可靠度的增加,部件的使用性能逐渐变差,对其维修所需的操作时间就会增多,并且不同的维修等级对部件进行维护所需的操作时间存在差异.如图3所示,当0<F<F1xi(xi=1或2)时,不同等级维护所需的时间都为最小维修操作时间tmin,且由于高级维护经验丰富、设备优良等客观原因,使得高级维护可以对更大区间的部件以最小维护时间完成任务(F11<F12).对处于相同不可靠度的部件进行高级维护所需的时间较少,且对初级维护来说,它的能力是有限的,无法承担较高不可靠度时的维修任务.

图3 不同维修类型所需操作时间与不可靠度的关系Fig.3 Relationship between unreliability and operation time for different maintenance actions
因此,第i次预防性维护时所需的操作时间为

式中:
xi=1或2;
F1xi表示初级维修或高级维修对部件进行维护时,操作时间为tmin的最大不可靠度;
Fmaxxi表示初级维护或高级维护所能承担的最大不可靠度;
tmaxxi为其对应的维护操作时间;
Fi为第i次预防性维护前部件的不可靠度值.
2.3 维护成本建模
部件一个更换周期内的总维护费用为

式中:
cr为部件小修的维修成本;
ci为每次预防性维护所需支付的费用,初级维护时为cj,高级维护时为cs,即
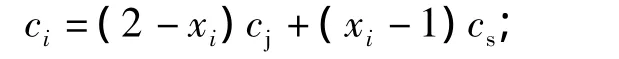
ca为部件与整车的维修等级不符造成的单次附加成本;
cw为部件更换时未达到最小可靠度而产生的价值浪费

式中:
cv为部件从初始状态到达到最低可靠度的利用价值.
2.4 目标函数
两种维护方案都选择在动车组的检修时机对部件实施维修,此时动车组没有运营任务,对部件进行维护所需的时间不会造成额外的停机损失.因此,维护时间和成本之间没有明确的关系,无法简化为单目标问题求解,只能对维护时间和维护成本同时进行优化,属于多目标优化问题.由以上建模可得到两种方案的优化模型.
方案1:
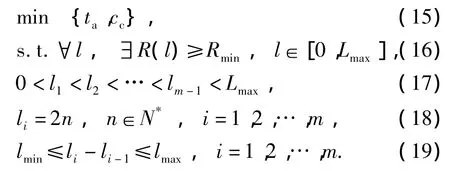
式(16)表示部件在研究区间内必须满足最低可靠度的要求;式(17)表示各维修时机间的顺序关系;由动车组的检修周期可知,每2万km都会对动车组进行检修,因此,只要选择在偶数里程时对部件进行维修就一定能保证部件的维修时机是选择在动车组整车的检修时机执行的,如式(18)所示;式(19)对维修周期进行限定,防止部件出现过维护和欠维护的情况.
方案2:
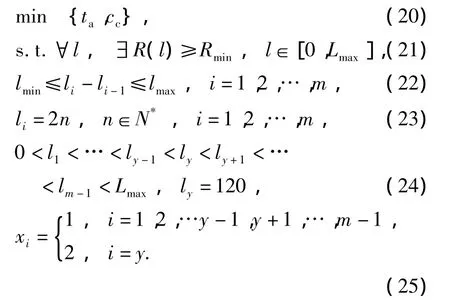
式(21)~(23)与方案1相同,式(24)~(25)表示部件的维修时机和维修级别约束,在动车组进行三级修(120万km)时对部件实施高级维修,其他都为初级维修.
3 求解方法
由于需要同时优化部件维护时机和维护级别,使得模型变得非常复杂,且两个优化目标维修总时间和维护成本间没有定量关系,属于多目标问题,求解相对复杂.本文采用多目标遗传算法[13](genetic algorithm,GA)对模型进行求解.
(1)编码和初始化种群
采用实值编码法对染色体进行编码.每条染色体分为两部分,前半部分用来记录预防性维护的执行时机,称为维修时机染色体.维修时机染色体中的基因用整数 li(i=1,2,…,m -1)表示,li∈[li-1+lmin,li-1+lmax]其中,l0=0.染色体中基因的个数由 lm-1∈[Lmax- lmax,Lmax)控制.
后半部分用来记录对应执行预防性维护的等级,称为维修等级染色体.维修等级染色体中的基因用xi表示,xi=1或2,个数与维修时机染色体中的基因个数一致.
按照约束条件随机得到种群数量染色体组成初始种群Pj(j=0),为了使后续操作方便,用“-1”将所有染色体补齐,将这部分称为无意义区.如区间为(0,200]、lmin=30、lmax=70 的一项任务,产生的初始种群如式(26)所示.

(2)交叉
本文采用单点交叉法同时对维修时机染色体和维修等级染色体进行交叉操作.即将Pj中的两个染色体作为父本,两染色体对应的交叉点位置之后的基因进行交换并将两个新个体储存在Qj+1中.若交叉点染色体不符合约束条件则重新选择交叉点.
(3)变异
对Qj+1中维修时机染色体或维修等级染色体进行单点变异操作,而其他位置的基因保持不变.当变异位置处于操作时机染色体时,按照维护时机规则重新生成一个里程将原数代替.当变异位置处于维护等级染色体时,变异采用1和2之间的替换.
经过变异后的染色体必须满足编码要求,如果变异后的染色体不符合约束条件,则重新进行变异.
(4)选择
多目标遗传算法是根据支配的概念运作的[14].对于多目标的问题,任意两个解 z1和 z2之间有以下二种关系:一个解支配另一个解;没有解支配另一个解.如果说z1支配z2,则必须同时满足两个条件:①对于所有的目标z1非劣于z2;② 至少有一个目标z1优于z2.多目标优化问题的所有非支配解组成了Pareto最优集.
第j+1代种群中的第g个个体zg在该代种群中有u个个体支配它,则它在种群中的秩为

按照本文的两个目标函数,每个个体的秩如图4所示.
Pareto最优集中所有非劣解的秩都是1.
按照式(10)和式(13)对 Zj+1=Pj∪Qj+1中所有个体的目标值进行求解,并按照式(27)计算出所有个体的秩.
若未达到循环次数j=j+1,并按秩从小到大选择出种群数量个解,储存在 Pj中,返回到步骤(2);若达到要求的循环次数,则选出秩为1的解,组成Pareto最优集.

图4 种群中个体的秩Fig.4 Pareto rank of the individuals in the population
4 算例
动车组四级检修里程Lmax为240万km;部件故障里程服从威布尔分布,η=100,β=2;运行期间的最小可靠度Rmin=0.6;初级维护可靠度恢复因子 θ1j=0.6,可靠度加速因子 θ2j=1.05;高级维护可靠度恢复因子θ1s=0.9,可靠度加速因子θ2j=1.02;可靠度改善因子 θ3=0.8.为避免过维护和欠维护(lmin=8,lmax=40).非完美维护时间和费用如表1所示.
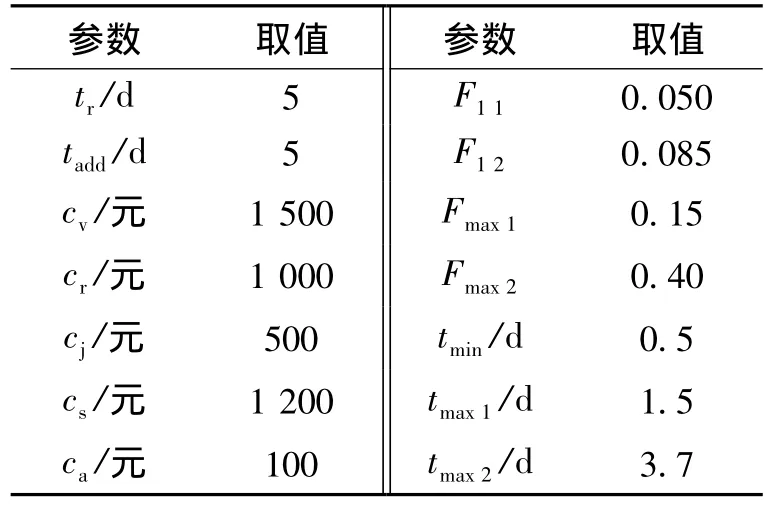
表1 维护参数Tab.1 Factors of maintenance
在Matlab R2012中编程实现求解该模型.终止条件为种群的代数达到指定代数100,种群规模为500,交叉概率为0.70,变异概率为0.05.两种维护方案的优化结果如表2所示,并编号为维修计划1至5.为比较本文提出的模型与单一非完美维护方式的优化模型的差异,在研究区间内只安排单一非完美维护的优化结果进行求解,如表3所示.
由表2与表3可以看出,在动车组四级修修程内若仅采用初级维护则无法得到满足条件的维修计划;若仅采用高级维护虽然可以得到满足条件的维修计划,但对部件的维修时间是两级非完美预防性维护策略下维修时间的近两倍,维修成本是两级非完美预防性维护策略下维修成本的 1.2~1.5倍.由此可以看出,两级非完美维护策略高于单一非完美维护的优越性.
由表2中两种维护方案的优化结果可以看出,按照方案1进行维护可以减少部件的维护次数,且维护费用较少,但是由于部件的维护等级会出现与整车维护等级不一致的情况,使得在总维护时间中增加了一部分额外的运输时间,造成部件生命周期内总维修时间增多.而方案2与动车组整车的维修计划更加贴合,部件随整车进行同等水平的维护,会减少管理部门额外的工作量,但付出的代价是对部件施行频繁的维护以使其满足可靠度要求,进而会使部件的维护成本增加.

表2 两级非完美预防性维护优化结果Tab.2 Optimization results of bi-level imperfect preventive maintenance
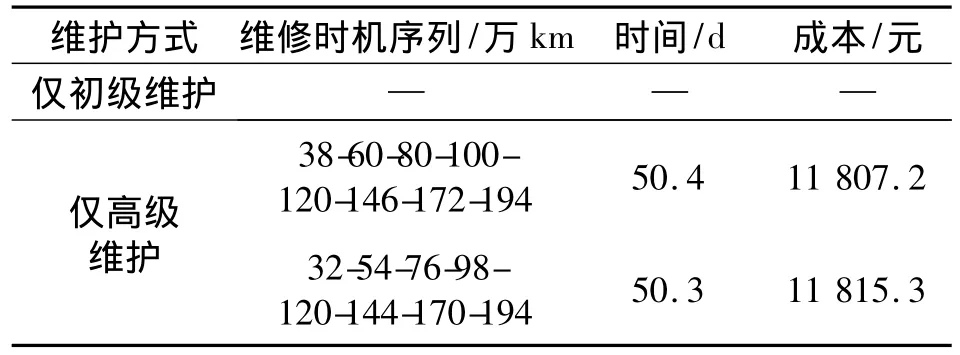
表3 单一非完美维护优化结果Tab.3 The results of single imperfect maintenance mode
多目标优化问题中多个目标同时达到最优的情况是不存在的.为对两种维护方案下的维护成本进行比较,选取维护时间最接近的计划1和4进行比较.由表2可知,维修计划1的期望维修时间只比计划4多2.98%,却节省了11%的维护成本.可靠度变化曲线如图5所示.

图5 维修计划1和4的可靠度变化Fig.5 Reliability change of maintenance schedule 1 and 4
由可靠度随里程的变化情况来看,按照维修计划1进行维护时能使部件在服役里程的后半部分中保持更高的可靠度.
5 结论
本文以动车组多级检修制度为背景,提出了多级非完美维护策略.在对我国动车组维护制度深入研究、做出必要假设的基础上,选取动车组四级修修程时更换的某部件为对象,建立了一种有两级非完美维护的模型.从优化结果可以看出,两等级非完美维护模型较以往单一非完美维护来说是一种更加经济合理的维护方式.配合我国动车组整车的维修计划,为部件制定了两种维护方案,方案1能够在较少的维修次数下使部件的可靠度保持在一个较高的水平,尤其是在部件服役里程的后半阶段,且其维修费用反而比方案2少.从经济性和安全性两个角度来看,方案1应该是更加合理的维护方式.在现阶段我国动车组开始进入四级修修程的背景下,本文建立的维护模型具有较强的现实意义.另外,在生产制造行业中对设备施行多级非完美维护的现象很普遍,所以本文中建立的两等级非完美维护可靠度模型对生产设备的维护也有实用意义.
[1]王连森,连苏宁.动车组维护与检修[M].成都:西南交通大学出版社,2010:9-20.
[2]PONCHET A,FOULADIRAD M,GRALL A.Imperfect condition-based maintenance assessment on a finite time span[C]∥ The Proceedings of2012 International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering and The 3rd International Conference on Maintenance Engineering(Vol.Ⅰ).Chengdu:IEEE,2012:390-395.
[3]夏唐斌,奚立峰,周晓军,等.串并联衰退系统的多目标预防性维护优化建模[J].计算机集成制造系统,2010,16(4):783-788.XIA Tangbin, XI Lifeng, ZHOU Xiaojun, et al.Optimization of multi-objective preventive maintenance for series-parallel deteriorating systems[J].Computer Integrated Manufacturing Systems,2010,16(4):783-788.
[4]WANG Jinran,YUE Xiaoyun,GUO Yajun,et al.Multi-state repairable system with imperfect preventive maintenance of the optimal maintenance strategy[C]∥Proceedings of2010 International Conference on Broadcast Technology and Multimedia Communication(Volume 5).Chongqing:IEEE,2010:149-152.
[5]ZHOU Xiaojun,XI Lifeng.A dynamic opportunistic maintenance policy for continuously monitored systems[J]. Journal of Quality in Maintenance Engineering,2006,12(3):294-305.
[6]黄傲林,李庆民,黎铁冰,等.劣化系统周期预防性维修策略的优化[J].系统工程与电子技术,2014,36(6):1103-1107.HUANG Aolin, LIQingmin, LITiebing, etal.Optimization of periodic preventive maintenance policies for deteriorating repairable system[J]. Systems Engineering and Electronics,2014,36(6):1103-1107.
[7]曲玉祥,吴甦.基于不完全维护的劣化系统分阶段顺序预防维护策略[J].机械工程学报,2011,47(10):164-170.QU Yuxiang,WU Su.Phasic sequential preventive maintenance policy based on imperfect maintenance for deteriorating systems[J]. Journal of Mechanical Engineering,2011,47(10):164-170.
[8]DOOSTPARAST M,KOLAHAN F,DOSTPARAST M.A reliability-based approach tooptimizepreventive maintenance scheduling for coherent systems[J].Reliability Engineering and System Safety,2014,126:98-106.
[9]金玉兰.生产系统有限时间区间弹性周期预防性维修策略研究[D].上海:上海交通大学,2009.
[10]董锡明.机车车辆运用可靠性工程[M].北京:中国铁道出版社,2002:6.
[11]D N PrabhakarMurthy, MichaelBulmer, JA Eccleston.Weibullmodelselection forreliability modeling[J]. Reliability Engineering and System Safety,2004,86(3):257-267.
[12]卜继玲,傅茂海.动车组结构可靠性与动力学[M].成都:西南交通大学出版社,2009:1-16.
[13]TSAI Y T,WANG K S,TENG H Y.Optimizing preventive maintenance for mechanical components using genetic algorithms[J].Reliability Engineering and System Safety,2001,74(1):89-97.
[14]OSMANA M S,ABO-SINNAB M A,MOUSA A A.An effective genetic algorithm approach to multiobjective routing problems (MORPs)[J].Applied Mathematics and Computation, 2005,163(2):769-781.
