关于修正的一维分子晶体模型的孤子激发

李琴兰，陈 浩

(华南师范大学物理与电信工程学院，广州510006)

1 引 言

在极性晶体中运动的电子，其库仑势使周围正负离子移位而产生极化，形成一个围绕电子的极化场. 极化场又反过来作用于电子，使其能量和状态等发生改变，并伴随着电子在晶格中运动这样一个相互作用的整体就是极化子. 极化子效应降低电子的能量，并使电子有效质量增加. 几十年来极化子问题一直在固体物理中扮演着相当重要的角色［1-4］. 近年来，由于低维系统非线性元激发的研究进展，重新引起人们对于一维极化子理论的兴趣. 而一维分子晶体模型中孤子激发态的存在也一直引起人们的重视，并已做过广泛的研究. 江涛［5］研究了一维分子晶体的极化子-孤立子运动，得到了带有孤立波形式的两类新的极化子- 孤立子解. 任学藻［6］等采用相干态展开法研究了一维分子晶体模型处于基态的极化子满足的带有积分形式的非线性薛定谔方程及其定态孤子解. 陈浩［7］等研究了Aharonov -Bohm 对环上带有色散项的分子晶体模型的光学极化子的影响.李圳［8］等研究了一维分子晶体模型中立方型相互作用引起的孤子激发. 本文研究关于修正的一维分子晶体模型的孤子激发解. 该修正解是在文献［8］的模型基础上加入了本征值平方项后得到的，通过分析本征值平方项和立方型相互作用对孤子激发的峰宽、峰值和电子自陷势阱的影响，我们可以看到本征值平方项有利于立方型相互作用的一维分子晶体模型中孤子的激发，改进了立方型相互作用对一维分子晶体模型孤子的弥散效应. 在忽略立方型相互作用和本征值平方项的影响后，该解与通常极化子解［1］一致.

2 运动方程和解

考虑立方型相互作用后的一维分子晶体模型的Hamiltonian 量为:

这一Hamiltonian 描述了一维系统中电子通过畸变与晶格光学振动发生相互作用，其中y 和m 分别是电子的坐标和质量，a 表示晶格间距，Rn= na 表示第n 个分子的位置，un表示第n 个分子

根据Holstein，我们可假定波函数:

满足Schrodinger. 这里an依赖于时间t 和晶格振动位移un，表示电子在第n 格点上的概率幅;φn(y，un)为第n 格点上的局域化的分子轨道，满足方程:

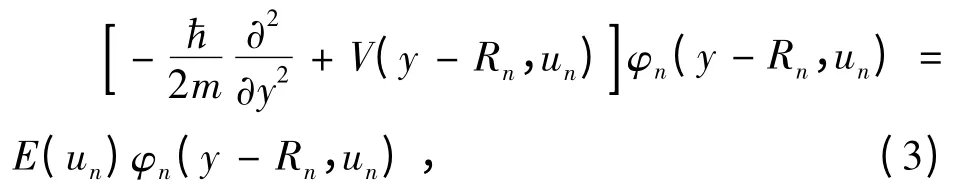
式中本征值E(un)只与分子振动的位移量un有关. 与往常的取线性近似不同，为了得到更准确的结果，我们将本征值取到平方项，即:

由式Schrodinger 方程，得到an的运动方程:

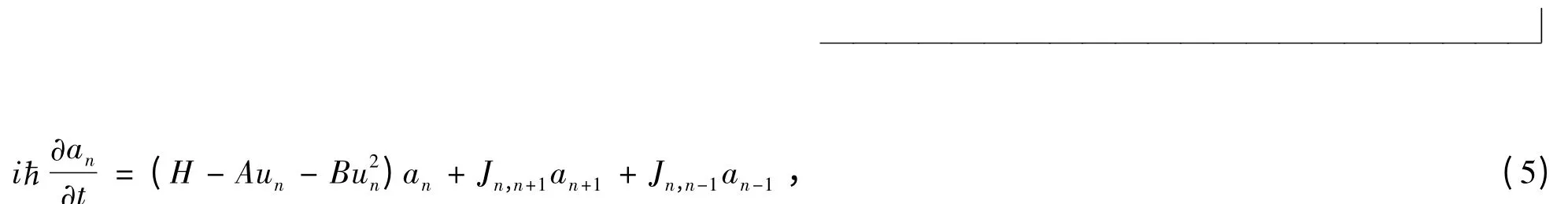
式中

是双中心交叠积分. - Aun-项代表电子与晶格间的相互作用势. 忽略Jn，n=1对un的依赖. 设Jn，n+1= - J，则:

取绝热近似，即略去式(6)中的晶格振动动能项，则得:

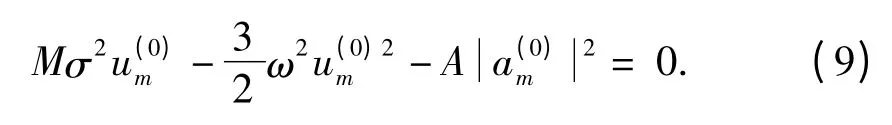
在ω2＜＜σ2时，上式的解为:

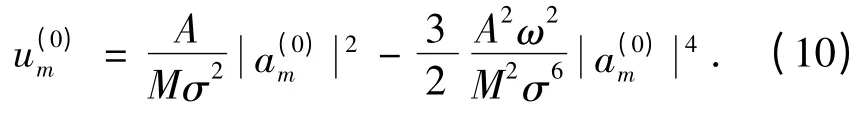
当a(0)n是n 的缓变函数时，可做下列连续化近似:

将式(10)、(11)代入式(7)可化解为:

3 讨 论

3.1 当ω2= 0 ，B = 0 时，即不考虑了立方型相互作用和本征值平方项时，孤子激发解回复于通常的极化子解［1］:

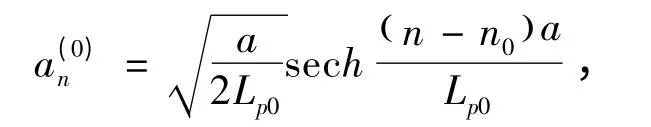
此时孤子的峰宽、峰值为(15)、 (17)式.由图3 可知，此时孤子激发的峰宽最窄，峰值最大，孤子特征最明显.

3.2 当ω2≠0 ，B = 0 时，由文献［8］可知，正比于ω2的项(即立方型相互作用项)是孤子的弥散项.

3.3 当ω2≠0 ，B ≠0 时，令α =，β =则式(12)化为:

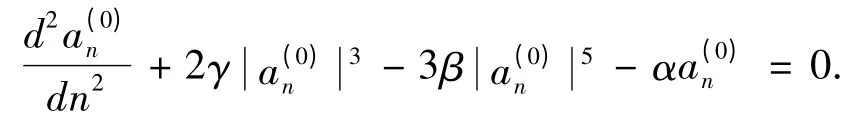
该方程的解为:

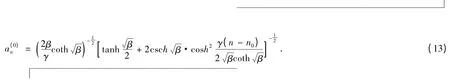
即在考虑立方型相互作用和本征值平方项后一维分子晶体模型的孤子激发的修正解可表述为式(13)，该孤子激发的峰宽和峰值变为:

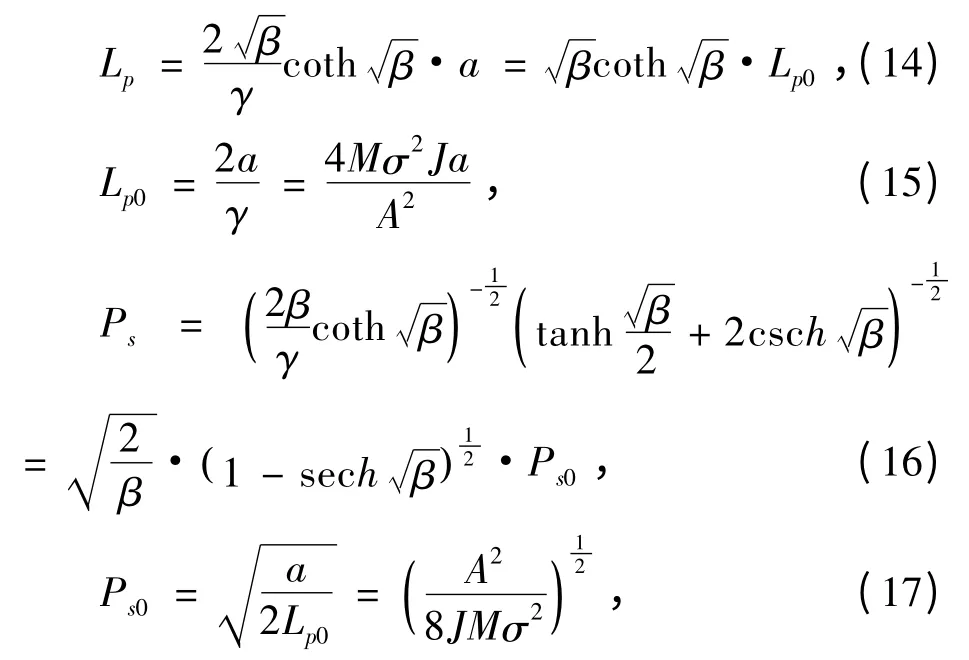
图1 孤子的宽度随β 的变化Fig.1 The change of the width of the soliton with the β

图2 孤子的峰值随β 的变化Fig.2 The change of the peak of the soliton with the β

以上是从数学角度分析了立方型相互作用和本征值平方项对一维分子晶体模型的孤子激发的影响，得到了有利于孤子激发的条件和不利于孤子激发的条件. 下面从物理意义上分析，理解他们对孤子激发的影响.

当ω2≠0 ，B ≠0 时，自陷态晶格振动位移为:

相应的电子自陷势阱则为:

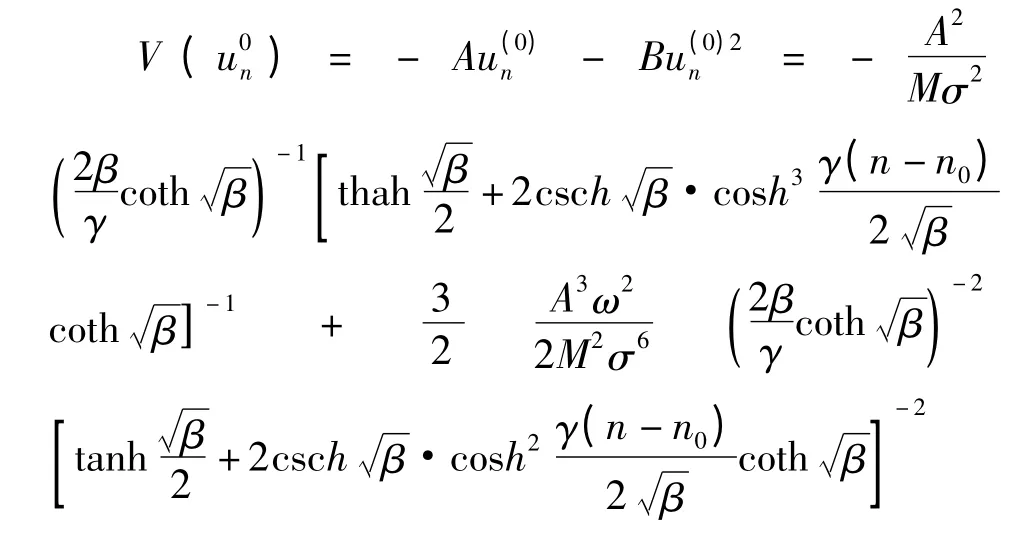
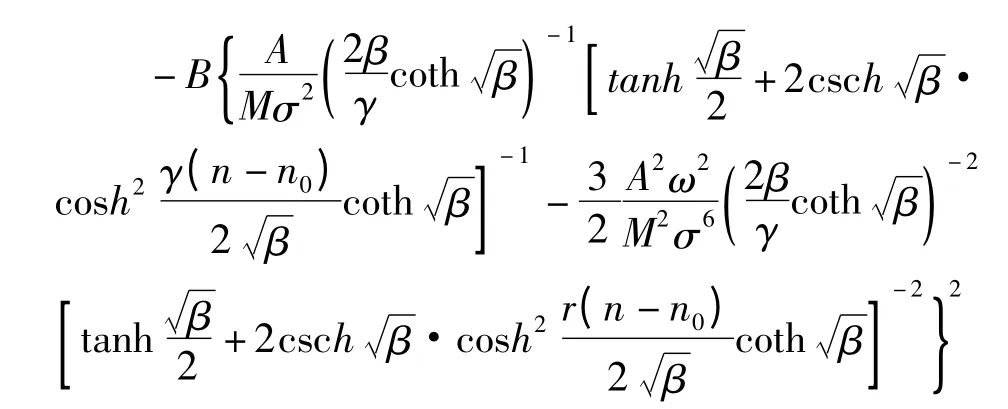
图3 β 取不同值时孤子解的比较Fig.3 The compare of solutions when β takes different values

在这里取A = 2，ω2=，分别画出的电子自陷势阱图，如图4.

图4 β 取不同值时电子自陷势阱图的比较Fig.4 The compare of the electron’s selftrapped potential well when β takes different values

4 结 论

在考虑立方型相互作用和本征值平方项后一维分子晶体模型的孤子激发的修正解跟通常孤子解相比较有很大的不同，他的孤子特征变的很不明显.

［1］ Holstein T. Studies of polaron motion. Part I. The molecular crystal model［J］. Ann. Phys.，1959，8:325.［2］ Chen H，Chen Y. On optical polarons in one dimensional molecular - crystal chains［J］. Chinese Phys.Lett.，1996，13:617.

［3］ Zhang C L，Jeckelmann E，White S R. Dynamical properties of one - dimensional Holstein model［J］.Phys. Rev. B，1999，60(20):14092.

［4］ Zhao C L，Wang L L，Zhao L L. The properties of ground state of polaron in quantum disk in finite depth potential well［J］. J. At. Mol. Phys.，30(4):637(in Chinese)［赵翠兰，王丽丽，赵丽丽. 有限深势阱里量子盘中极化子的基态性质［J］. 原子与分子物理学报，2013，30(4):637］

［5］ Jiang T. Polaron solitons motion in one -dimensional molecular crystals［J］. J. Henan Univ.:Natural Science Edition，2003，33(3):17(in Chinese)［江涛.一维分子晶体的极化子-孤立子运动［J］. 河南大学学报:自然科学版，2003，33(3):17］［6］ Ren X Z，Liao X，Liu T，et al. Polaron of one -dimensional molecular crystals［J］. J. At. Mol. Phys.，2006，23(4):616(in Chinese)［任学藻，廖旭，刘涛，等. 一维分子晶体中的极化子［J］. 原子与分子物理学报，2006，23(4):616］

［7］ Chen H，Chen Y. Influence of the Aharonov -Bohm flux on the optical polarons in the molecular - crystal model with the dispersion term in a ring［J］. Solid State Commun.，1998，105(8):537.

［8］ Li Z，Chen H. Soliton excitation of a one-dimensional molecular-crystal model with a cubic interaction term［J］. J. South China Normal Univ.:Natural Science Edition，2011，(1):62(in Chinese)［李圳，陈浩.一维分子晶体模型中立方型相互作用引起的孤子激发［J］. 华南师范大学学报:自然科学版，2011，(1):62］

［9］ Li Z Z. Solid Theory［M］. 2nded. Beijing:Higher education Press，2002:363(in Chinese)［李正中. 固体理论［M］.2 版. 北京:高等教育出版社，2002:363］