Mn 掺杂GaN 稀磁半导体的电磁特性研究

毋志民，王 蒙，邓军权

(重庆师范大学物理与电子工程学院，重庆401331)

1 引 言

稀磁半导体(diluted magnetic semiconductor，DMS)是指Ⅱ-Ⅳ族或Ⅲ-Ⅴ族化合物半导体中，由磁性过渡族金属离子或稀土金属离子部分替代非磁性阳离子所形成的一类新型半导体材料［1，2］.因具有许多新奇的物理效应如大g 因子的磁性，法拉第旋转，巨磁阻，磁光效应等，在自旋电子学以及光电子领域已经展现出非常广阔的应用前景，可以制成各种新型的功能器件如自旋阀、自旋二极管、逻辑器件、高速光开关、高密度非易失性存储器、磁感应器、光隔离器件和半导体激光器集成电路以及量子计算机等. 同时DMS 的发展与实用化也为探索新的物理效应与新的应用特性提供了重要可能，引起人们的广泛关注［3-6］.

而作为第三代半导体材料的代表，GaN 基半导体材料不但拥有良好的光电性质以及宽的直接带隙(Eg=3.39 eV)，还有较高的击穿场强、高的热导率和非常好的物理、化学及热稳定性等，使其成为微波器件、光电子器件、高温器件方面的首选材料，并且非常适合制作抗辐射、高频、大功率和高密度集成的电子器件，是目前世界上较为先进的半导体材料之一. 对于稀磁半导体，自旋注入是实现自旋电子器件的首要条件，特别是如何实现在室温下自旋极化电子注入是人们关注的焦点［1，7-10］. 而大量的研究表明Mn 掺杂GaN的居里温度(Tc)可高于室温［7-10］，同时具有半金属性，是理想的自旋电子材料. 由于Mn2+离子的电子组态最外层为半满，自旋量子数s =5/2，其有效磁矩(有效玻尔磁子数)μeff=5.92μB，所以在过渡族元素中，Mn2+离子的掺杂效应最明显. Katayama - Yoshida 等人［11］采用密度泛函理论(DFT)研究了Mn 掺杂GaN，发现Ga1-xMnxN(x=0.25)具有稳定的铁磁基态;Sato 等人［12］采用Korringa-Kohn-Rostoker 方法的相干近似理论计算研究了Mn 掺杂GaN，结果表明，低Mn 浓度掺杂时具有稳定的自旋玻璃态，高Mn 浓度掺杂时具有稳定的铁磁态. Sanyl 等人［13］采用LSDA和LSDA+U 计算表明同Mn 掺杂GaAs 不同，Mn掺杂GaN 使Mn 的d 电子形成了一个与本征价带完全分离的杂质带，其铁磁性源于Mn 团簇内短程的双交换作用，且高掺杂表现为铁磁金属性.

虽然目前已成功制备了Tc高于室温的(Ga，Mn)N 薄膜，但人们对其磁性机理还未能形成一个统一的理论共识，且材料多表现为高阻抗，不利于研究其磁传输特性. 为了对Mn 掺杂GaN(Ga1-xMnxN)的电子结构和磁性有更为深入的认识，本文采用基于密度泛函理论(DFT)的平面波赝势法(PWP)，计算了未掺杂的GaN 和不同Mn 浓度掺杂GaN (Ga1-xMnxN，x = 0.0625 和0.1250)的晶体结构、能带图和态密度，分析并比较了其电子结构和磁性，以便为实验研究提供有意义的数据参考.

2 模型结构和计算方法

2.1 模型构建

理想GaN 为无色透明晶体，多为六方纤锌矿结构［1］，属于P63mc 空间群，对称性为C6v-4，晶格参数a=b=0.3189 nm，c=0.5185 nm，α=β =90°，γ=120° ，其中c/a 为1.626，比理想六角密堆积结构的1.633 小，其晶胞由Ga 的六角密堆积与N 的六角密堆积反向套构而成. 文中计算基于超晶胞模型，根据Mn 掺杂的浓度x (x = 0.0625和0.1250)的不同，分别选取32 个原子(2 ×2×2)和16 个原子(2 ×2 ×1)超晶胞体系，在每个超晶胞中掺杂一个Mn 原子. 图1 为选取的纯的GaN 和掺杂Mn 原子过后的32 个原子超晶胞体系的模型结构.

图1 Ga1-xMnxN 32 原子体系超晶胞结构图:(a)x=0 ;(b)x=0.0625Fig.1 32 atoms supercell structures of Ga1-xMnxN:(a)x=0 ;(b)x=0.0625

2.2 计算方法

本文的计算工作是由基于密度泛函理论(DFT)的从头算量子力学程序CASTEP［14］完成的. 计算中采用周期性边界条件，并采用超软赝势来描述离子实与价电子之间的相互作用，在Mn掺杂GaN (Ga1-xMnxN)体系中，Ga、N、Mn 的价电子组态分别选取为 Ga:3d104s24p1，N:2s22p3，Mn:3d54s2，并将Mn 的初始自旋态设定为自旋向上. 在倒易的K 空间中，选取平面波截止能Ecut=380.0eV，交换关联势采用GGA -PBE近似法，并对16 个原子和32 个原子超晶胞体系选择K 网格点为2 ×2 ×2. 为了保证体系能量在平面波基水平上的收敛，原子的最大位移的收敛标准是0.0001nm，原子间相互作用力的收敛标准是0.003 eV·nm-1，单原子的能量的收敛标准设定为1.0 ×10-5eV·atom-1，晶体的内应力收敛标准是0.05 GPa. 为了使计算结果相对精确，计算中先优化晶胞结构，根据所得晶胞参数再优化内坐标，再计算Ga1-xMnxN 体系的晶格常数、能带结构和态密度.

3 计算结果与讨论

3.1 纯GaN 的电子结构

为了便于与不同浓度Mn 掺杂GaN 后的电子结构进行分析比较，文中先计算了未掺杂的GaN电子结构. 计算中先对GaN 原胞进行结构优化，所得晶格结构参数与实验值的比较如表1 所示，可以看出结构优化后的a = b =0.3221 nm，c =0.5256 nm，c/a =1.632，与实验值［1］大致相符，说明本文所采用的计算方法是合理的.

表1 优化后GaN 晶格参数与实验值［1］的比较Table 1 The optimized and experimental［1］lattice constants of GaN

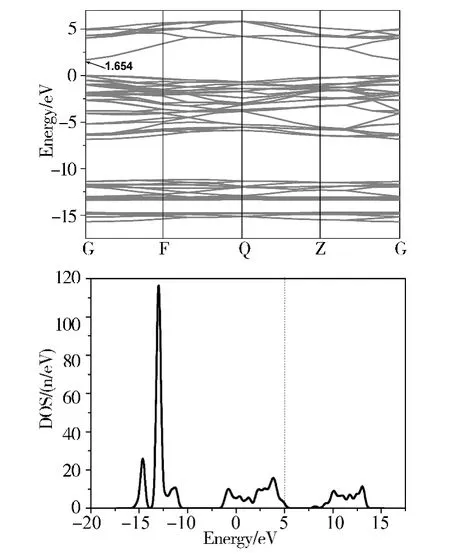
图2 GaN 的能带结构(a)和总态密度(b)Fig.2 The band structure (a)and total DOS (b)of GaN

图2 (a)为GaN 的能带结构图，可以看出，GaN 的能带由导带，上价带和下价带三部分构成.其中导带占1.7—5.0 eV，上价带占-6.8—0 eV，下价带占-15.7 —-11.3 eV. 图中的导带底和价带顶均位于Brillouin 区的G 点处，说明纯的GaN 为直接禁带半导体，带隙值Eg=1.654eV，与邢海英等人［1］计算所得的结果大致相符. 图2(b)和图3 分别为GaN 总的态密度图和分波态密度图，可以看出，GaN 的导带主要来源于Ga 4s，Ga 4p 态电子，以及少量的N 2s，N 2p 态电子;上价带主要来源于N 2p，Ga 4p，Ga 4s 和少量的N 2s 态电子;下价带主要来源于Ga 3d，N 2s 及少量的Ga 4s，Ga 4p 和N 2p 态电子. 理论计算所得的带隙值与实验值Eg= 3.39 eV 相比偏低，这是因为计算中采用的DFT 为基态理论，而能隙属于激发态，因此计算结果偏低，这也是采用该理论计算时普遍存在的现象［15］，但并不影响对GaN 及其掺杂体系电子结构和磁性的理论分析.

图3 GaN 的分波态密度:(a)Ga ;(b)NFig.3 The partial DOS of GaN:(a)Ga ;(b)N

3.2 Mn 掺杂GaN 的电子结构和磁性

表2 为Mn 掺杂浓度分别为0.0625 和0.1250时Ga1-xMnxN 优化后的晶格参数. 可以看出掺杂后的材料的晶格常数略微有所增大，但c/a ≈1.63，基本没有变化，这是由于Mn 与Ga 原子(离子)半径相差不大，以及在计算的时掺杂浓度不高造成的. 由表2 可以出，不同浓度的Mn 原子掺杂GaN (Ga1-xMnxN)也不会引起明显的晶格畸变.

图4 为Ga1-xMnxN (x =0.0625 和0.1250)的自旋极化能带结构图. 可以看出不同Mn 浓度掺杂后，导带底和价带顶位均位于Brillouin 区的G 点处，因此掺杂后的Ga1-xMnxN 仍为直接禁带半导体. 由表3 可知，随着Mn 的掺入，体系的带隙显著增加. 图4 (a)中p 代表N 离子的p 能带，d1与d2代表Mn 离子的d 能带. 由图可以看出，N 的p 能带相比Mn 的3d 能带处于远离费米能级(EF)的深处，Mn 的3d 能带处于相对较浅的能级中，Mn 的d1与d2能带位于N 的p 之上，这主要是由于N 的电负性较强. 另外由于N 的原子半径较小，d1和d2两能带空间分布的对称性相同，因而Mn 的d1与N 与p 之间相互作用比较强，将Mn 的d1能带向上推，N 的p 能带向下推，从而使得Eg值增大［1］. 因为GaN 是抗磁性的，而Mn 是磁性元素，因此当掺杂了Mn 之后，在磁学性质上发生了很大的变化. 磁性离子间的反铁磁相互作用导致顺磁、自旋玻璃转变和反铁磁性等;而磁性离子间的铁磁相互作用导致顺磁和铁磁性等［16］. 无掺杂的半导体的自旋向上与自旋向下的能带相同，未产生能带(自旋)劈裂，因此纯的GaN 没有磁性. 当Mn 原子掺入后，上下自旋产生劈裂，表明掺杂体系存在一定的半金属铁磁性.

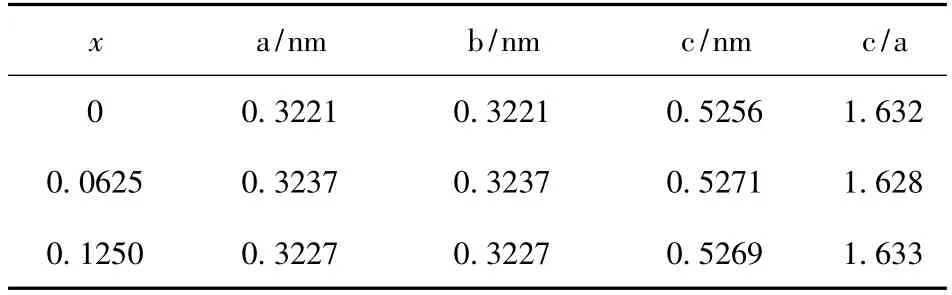
表2 Ga1-xMnxN (x=0.0625 和0.1250)的晶格参数Table 2 Lattice constants of Ga1-x MnxN (x =0.0625 and 0.1250)

图4 Ga1-xMnxN 的自旋极化能带结构:(a) (b)x =0.0625;(c)(d)x=0.01250Fig.4 The spin polarized band structure of Ga1-x MnxN:(a)(b)x=0.0625;(c)(d)x=0.01250

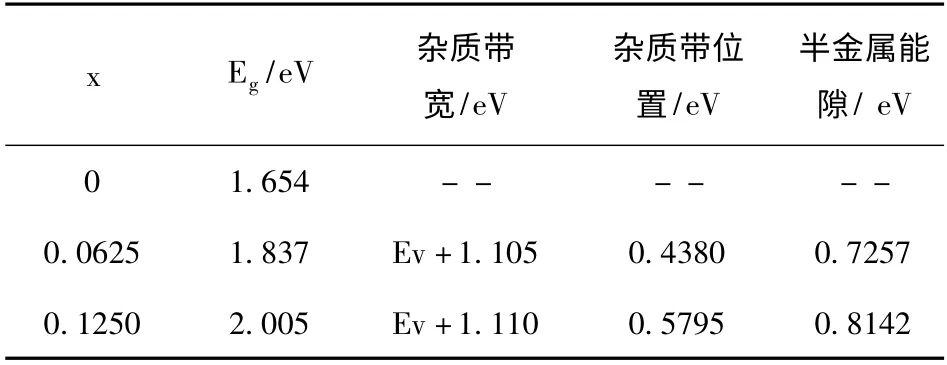
表3 不同Mn 浓度掺杂GaN 带隙相关值Table 3 The related values of band gap of GaN with different Mn doped concentration

由图4 和表3 可以看出，掺Mn 的能带图中一个明显的现象是出现与Mn 有关的位于价带顶上方的自旋极化杂质带，随着Mn 掺杂浓度的增加，杂质带宽度逐渐增大，由0.4380 eV 增加到0.5795 eV，分别位于价带顶上方1.105 eV 和1.110 eV 处，为深受主能级. 自旋向上子带穿过EF，而自旋向下子带与导带底合并，因此材料表现为半金属性. 随着Mn 的掺入，半金属能隙由0.7257 eV 增大到0.8142 eV，半金属能隙逐渐变宽，半金属稳定性逐渐增强. 在自旋向上部分中含有自旋极化杂质带，沿Brillouin 区方向表现出弥散特性. 自旋向上的能带占据费米面，而自旋向下的未占据费米面，明显表现为自旋注入，即杂质带中通过有效质量传输产生100 % 的自旋极化载荷子注入. 此外，Mn 的掺入使得导带显著自旋极化，而价带没有产生自旋极化.

图5 Ga1-xMnxN 的自旋极化态密度:(a)x =0.0625;(b)x=0.1250Fig.5 The spin polarized DOS of Ga1-x MnxN:(a)x =0.0625;(b)x=0.1250

图5 为Ga1-xMnxN (x =0.0625 和0.1250)的自旋极化态密度图. 可以看出，Mn 的掺入引入了自旋极化杂质带，且费米能级位于杂质带中，没有改变材料的半导体性质. 在理想情况下，如果载荷子在其中具有足够的迁移率，那么从Ga1-xMnxN 注入的载流子将产生100 %的自旋极化［1］.图5 表明，该自旋向上杂质带是由Mn 的3d 杂质带与N 的2p 轨道杂化而展宽的分离能带. 价带没有产生有效自旋极化，主要是因为在价带中Mn的3d 态对自旋向下的贡献与自旋向上的贡献相差不大;在导带底可以看到自旋向下的Mn 的3d能级与N 的2p 发生较弱的轨道杂化.

4 结 论

采用基于密度泛函理论的第一性原理平面波赝势法计算了不同浓度Mn 原子掺杂GaN (Ga1-xMnxN)的晶格常数、能带结构和态密度，分析比较了纯GaN 和不同浓度Mn 掺杂GaN 的电子结构和铁磁性. 计算结果表明:纯GaN 和掺杂不同浓度Mn 的GaN 的导带底和价带顶均位于Brillouin区的G 点处，均为直接禁带半导体;随着Mn 掺杂浓度的增加，由于出现与Mn 有关的杂质带，体系的带隙Eg逐渐变宽. 纯GaN 没有磁性，而Mn原子掺杂GaN 使得Mn 3d 与N 2p 轨道杂化，产生自旋极化杂质带，杂质带宽度随Mn 浓度的增加逐渐增大，自旋向上的能带占据费米面，而自旋向下的未占据费米面，呈现一定的半金属铁磁性.掺杂Mn 原子之后的Ga1-xMnxN 的能带图中，EF均贯穿在杂质带中，明显表现为半金属性，适合自旋注入;随着Mn 浓度的增加，体系半金属能隙逐渐增大，稳定性有所增强.

［1］ Xing H Y，Fan G H，Zhao D G，et al. Electronic structure and optical properties of GaN with Mn-doping［J］.Acta Phys. Sin.，2008，57(10):6513 (in Chinese)［邢海英，范广涵，赵德刚，等. Mn 掺杂GaN 电子结构和光学性质研究［J］.物理学报，2008，57(10):6513］

［2］ Chen C P，Xie J X，Chen S B. Electronic structure and optical properties of ZnS doped with Ti and Al［J］. J. At. Mol. Phys.，2013，30(1):149(in Chinese)［陈长鹏，谢建雄，陈水波. Ti 和Al 共掺杂ZnS 的电子结构和光学性质［J］.原子与分子物理学报，2013，30(1):149］

［3］ Shen S. Optical and transport studies of magnetic semiconductors［D］. University of Notre Dame，Notre Dame，Indiana，USA，2009:1.

［4］ Cheng S J. Theory of magnetism in diluted magnetic semiconductor nanocrystals［J］. Phys. Rev. B，2008，77 (11):115310.

［5］ Jungwirth T，Novák V，Martí X，et al. Demonstration of molecular beam epitaxy and a semicon ducting band structure for I - Mn - V compounds［J］. Phys. Rev.B，2011，83(3):035321.

［6］ Wijnheijmer A P，Martí X，Holy V，et al. Koenraad scanning tunneling microscopy reveals LiMnAs is a room temperature anti - ferromagnetic semiconductor［J］. Appl. Phys. Lett.，2012，100:112107.

［7］ Crooker S A，Furis M，Lou X，et al. Imaging spin transport in lateral ferromagnet/semiconductor structures［J］. Science，2005，309:2191.

［8］ Van Schilfgaarde M，Mryasov O N. Anomalous exchange interactions in III - V dilute magnetic semiconductors［J］. Phys. Rev. B，2001，63:2332052.

［9］ Jungwirth T，Kênig J，Sinova J，et al. Curie temperature trends in (III，Mn)V ferromagnetic semiconductors［J］. Phys. Rev. B，2002，66:0124022.

［10］ Sato K，Bergqvist L，Kudrnovsky J，et al. First -principles theory of dilute magnetic semiconductors［J］. Rev. Mod. Phys.，2010，82:1633.

［11］ Katayama - Yoshida H，Kato R，Yamamoto T. New valence control and spin control method in GaN and AlN by codoping and transition atom doping［J］. J.Cryst. Growth，2001，231(3):428.

［12］ Sato K，Katayama - Yoshida H. Material design of GaN-based ferromagnetic diluted magnetic semiconductors［J］. Jpn. J. Appl. Phys.，2001，40:L485.

［13］ Sanyal B，Bengone O，Mirbt S. Electronic and magnetism of Mn -doped GaN［J］. Phys. Rev. B，68:205210.

［14］ Segall M D，Lindan P，Probet M J，et al. First-principles simulation:ideas，illustrations and the CASTEP code［J］. J. Phys.:Condens. Matter.，2002，14:2717.

［15］ Shang G，Peacock P W，Robertson J. Stability and band offsets of nitro generated high -dielectric -constant gate oxides［J］. Appl. Phys. Lett.，2004，84:106.

［16］ Guo J M. Preparation and properties of GaN based diluted magnetic semiconductors［D］. Hebei:Hebei normal university，2008:1(in Chinese)［郭俊梅. GaN基稀磁半导体的制备与性质研究［D］. 河北:河北师范大学，2008:1］