基于标签的矩阵型Gröbner基算法研究

潘森杉胡予濮 王保仓

(西安电子科技大学综合业务网国家重点实验室 西安 710071)

基于标签的矩阵型Gröbner基算法研究

潘森杉*胡予濮 王保仓

(西安电子科技大学综合业务网国家重点实验室 西安 710071)

目前基于标签的Gröbner基算法大多是Buchberger型的，涉及矩阵型算法的文献往往是为了进行复杂度分析，而不考虑实际的效率。该文从实际应用出发，给出矩阵型Gao-Volny-Wang(GVW)算法的一个实例，提出算法层次的优化设计方法。同时，该文还给出一个高效的约化准则。通过实验，该文比较了算法可用的各项准则及策略。实验结果表明，该文的矩阵型GVW实例在准则和策略的选取上是最优的。并且，矩阵型GVW在某些多项式系统(例如，Cyclic系列和Katsura系列多项式系统)下比Buchberger型GVW要快2～6倍。

密码学；Gröbner基；标签；多项式；Gao-Volny-Wang (GVW)算法

1 引言

Gröbner基是求解多元多项式系统的一个基本数学工具。求出了多项式组的Gröbner基，多项式系统的解就能很快算出。这一工具广泛应用于编码理论、密码学乃至物理、生物等自然科学领域。1965年，Buchberger[1]提出了第1个Gröbner基求解算法。1983年，为了分析Buchberger算法的复杂度，Lazard引入了线性代数的方法[2]。随后Faugère提出了基于线性代数的F4算法[3]和基于标签的F5算法[4]。F4, F5算法是目前公认的两个高效Gröbner基求解算法。Faugère和Joux在文献[5]中使用了矩阵F5算法成功地攻破了隐藏域方程(Hidden Field Equations, HFE)公钥密码系统的第1个挑战(80 bit)。虽然源码未曾公开，文献[6, 7]给出其算法的伪代码，文献[8]给出一个更详细的矩阵算法版本。矩阵F5算法的核心思想是借鉴F4中线性代数的方法来同时约化多个多项式。但是到目前为止没有任何文献专门研究矩阵型F5和Buchberger型F5孰优孰劣和如何设计准则和策略高效实现矩阵型F5。唯一可以知道的是，文献[9, 10]都有提及矩阵型F5一般要比F5算法要低效。

近年来涌现出一批基于标签的Gröbner基算法，例如Arri-Perry(AP)[11], Gao-Guan-Volny(G2V)算法[12]和Gao-Volny-Wang(GVW)算法[13]。它们都使用了Buchberger风格，但它们似乎又与F5算法截然不同。什么样的策略和准则对算法的帮助较大是一个值得研究的问题。

本文研究了矩阵型GVW算法的应用准则、策略和实现技巧。在设计上，为了减小约化的开销，本文采用了延迟求模的方法。在预处理过程中，本文对Macaulay矩阵进行并行化构造。除此之外，还使用了一个更高效的约化准则。在实现上，本文比较了在不同的模序、c-对选取序、重写序下的矩阵型GVW算法的实际效果。而且，实验得出了矩阵型GVW算法在某些多项式系统下要比Buchberger型GVW算法快2～6倍。最后本文还将其与突变GVW (M-GVW)算法[14]相比较，结果表明矩阵型GVW算法优势明显。

2 预备知识

令R=K[x1,x2,…,xn]为域K上的n变量多项式环，M为单项式

≤记为M上的可允许单项式序。R上的一个非零多项式p能写成关于序≤的单项式K线性组合：，其中ca∈K{0}, xa∈M, A为ℕn上的一个有限集。如果xb是集合{xa|a∈A}的最大单项式，那么HM(p)=xb(相应地，HT(p)=cbxb, HC(p)=cb)叫做p关于≤的首单项式(相应地，首项，首项系数)。p的次数记为deg(p)，若p≠0其次数为，否则为-1。

令I为集合F={f1,f2,…,fd}∈R生成的理想，即I ={u1f1+u2f2…+udfd|u1,u2,…,ud∈R}。考虑映射：其中ei是Rd的第i个单位向量使得自由R-模Rd由集合Σ={e1,e2,…,ed}生成。本文在Md={mei|m∈M,i∈[1,d]}上定义一个模序≤s与≤适配}(见文献[15, 16]): m≤t⇒mei≤stei。如果不产生歧义，≤s简记为≤。L={(max{HM(ui)ei,≤},p)|φ(u) =p∈I}被叫作ℓ-多项式的集合，其中u =。令α=(s,p)∈L*，其中L*=L (0,0)，第1部分s =max{HM(ui)ei,≤}叫做α的标签，记为S(α)，第2部分p=poly(α)是其多项式部分。不失一般性，本文假定poly(α)总是首一的。同样，定义α的首单项式为HM(α)=HM(p)，次数为

deg(α)=deg(S(α))=max{deg(ui)} 。如果S(α)=tej，就把idx(α)=j记为其索引。s-次数(见文献[17]) 定义为degs(α)=deg(S(α))+deg(fidx(α))。子集Syz= {(s,0)∈L*}叫做L的合冲子模，NS=LSyz 被叫作非合冲多项式集。令(s1,p1)和(s2,p2)是NS中的两个非合冲ℓ-多项式。由形如(p2s1−p1s2,0)的合冲生成的模叫做主合冲子模PS。

一个ℓ-多项式α∈L是可预测的，如果一个Gröbner基算法已经找到一个合冲δ∈Syz使得S(δ)|S(α)。算法应当避免计算这样的α，因此其被称为冗余的。

α∈NS 被称为是关于B⊂L*首可约的，若存在一个ℓ-多项式β∈B满足下列条件之一，

(1)HM(tβ)=HM(α)且S(tβ)＜S(α);

(2)S(tβ)=S(α)且HM(tβ)＜HM(α);

(3)HM(tβ)=HM(α)且S(tβ)=S(α), t∈M。

否则，α关于B首不可约。

α−t β这一操作叫做S-约化 (对应的，M-约化，超首约化)，若满足条件(1) (对应的，条件(2)，条件(3))。条件(1)中，β和tβ分别被称为S-约化子和乘性S-约化子。有时tβ也简称为S-约化子。令γ为用α去S-约化tβ的结果，这一过程可表示成是的自反传递闭包，即反复执行约化操作直到得到一个S-不可约的ℓ-多项式。若不考虑标签的大小关系，这样的约化叫做c-约化。

由文献[11]和文献[16]的结论可得到如下的性质。

引理1 令α为NS中的非合冲元．α是可以被L*来M-约化的，当且仅当它是可以被L*来S-约化的。

利用上述引理的逆否命题，本文得出如下结果。

推论1[18]令α,β∈L*使S(α)=S(β)且它们非合冲。若α和β都S-不可约，则HM(α)=HM(β)。

由文献[17]可知，若α∈NS是齐次的，deg(α)=degs(α)，否则deg(α)≤degs(α)。

若α是S-不可约的且deg(α)＜degs(α)，则称其为一个突变 (原始定义见文献[19])。如果输入多项式是齐次的，那么NS中是不存在突变的。

一个集合G⊂L叫做模L的S-Gröbner基，如果任意的非合冲α∈NS能够被G首约化。

由引理1可知，I中的每个非零多项式可以被I的Gröbner基{poly(α)|α∈G,poly(α)≠0}约化。因此S-Gröbner基实际上是文献[11]的一个术语，它是文献[20]中“强Gröbner基”的精简版。由上述定义可知，合冲ℓ-多项式不是S-Gröbner基的必要组成部分。本文说两个ℓ-多项式α和β等价，如果S(α)=S(β)且HM(α)=HM(β)。显然，所有的非合冲首不可约ℓ-多项式组成具有最少个数的S-Gröbner基。文献[11]，文献[21]和文献[16]指出，非合冲不可约ℓ-多项式只有有限多个(不计等价)。

3 重写序

本文引入文献[18]中定义在G上的关于重写准则的概念。一个ℓ-多项式α∈G是标签s的重写子，如果α是G中使得S(tα)=s的-最大元素，其中t∈M,为G上一个线性序(称为重写序)。与文献[18]相比，这里对没有过多的限制：它只要是G上的线性序即可。有时本文也把tα叫做s的重写子。mβ∈M×G 是可重写的，如果S(mβ)的重写子是α≠β。现在用的最多的是两种重写序是文献[18]中的r和文献[4]Rules集合中元素的排序(记为new)。它们的定义如下：

令α,β∈NS ,Γαβ记为最小公倍数lcm(HM(α), HM(β))。令mα=且。若r(α)＞r(β), mαα在文献[13]中被称为α和β的J-对。(α,β)叫做c-对，deg(Γαβ)叫做c-对(α,β)的(全)次数。r(α)＞r(β)时，degs(mαα)叫做c-对的s-次数。

4 矩阵型Gröbner基算法

首先，本文引入文献[18]中关于重写基的一些术语。G是标签s的重写基，如果s的重写子tα∈M×G 不是S-可约化的。对于所有小于s的标签s'，如果G是标签s'的重写基，那么G被称为直到s的重写基(记为G)。ℓ-多项式集L＜s的S-Gröbner基也可以记为G。记号G和G有类似的定义。

G，如果α是首不可约ℓ-多项式且S(α)＜s，则G中有另一ℓ-多项式与α等价。

证明略。

为了与文献[14]的M-GVW算法作比较，这里假设e1＞e2…＞ed。与文献[22]一样，本文可以推导出e1,e2,…,ed为首不可约标签。

给定一组多项式，矩阵型GVW算法求出其理想的Gröbner基，其中，sort(F,≤) (相应地，min(F,≤)) 表示按序“≤”排列 (相应地，选取)集合F中的元素。顾名思义，cpair(α,β) 为α 和β组成的c-对。spoly(α,β) 表示α 和β 的s-多项式mαα−mββ, concat(A,B)的意思是把集合B中的元素排到集合A的后面。子算法S-REDUCE利用G来反复s-约化ℓ-多项式组V，记录下具有新的首项的不可约ℓ-多项式。对于ℓ-多项式组V的所有单项式，子算法SYMBOLIC_PREPROCESS的目的是寻找满足准则的c-约化子。如果将这些约化子的系数分别写进矩阵的各行，本文就构造出了Macaulay矩阵。

这里不给出矩阵型GVW算法，因其伪代码与文献[14]基本相同，本节将着重介绍对其子算法的改进及优化。

与矩阵型算法相对应的是Buchberger型算法，即算法每次只选择一个c-对。对于计算S-Gröbner基的算法，文献[13]的实验得出两个高效的模序，记为≤POT(位置先于项)和≤SR(Schreyer 见文献[23])，它们的定义如下：

mei≤POTtej，如果i＜j，或者i=j, m≤t，其中m,t∈M。

mei≤SRtej，如果HM(mfi)＜HM(tfj)，或者HM(mfi)=HM(tfj), i＜j。

矩阵型GVW算法的正确终止性证明可利用推论2，对标签s进行数学归纳得到，细节可以参见文献[13, 14]，这里不再赘述。本节主要讨论算法的优化设计，部分方法借鉴了Fayssal Martani对矩阵F4算法的优化实现。

4.1 延迟求模

约化操作是Gröbner基算法中开销最大的部分，当基域较小时，每次约化后多项式系数都要作求模操作。一个自然的想法就是延迟求模运算，即S-约化得到S-不可约多项式之后再对各多项式求模。这一技巧能加速计算Gröbner基，特别是当基域是F2的时候。算法S-REDUCE用H来记录s-约化为零的那些合冲组成的子模。

4.2 高效约化准则

注意到，在选取tβ的时候，通常的做法是确保tβ的标签为非合冲的，并且使tβ不能被重写。实际上，如果算法检查每个S-约化子是否满足这两个准则，那么算法的效率是相当低下的。所以本文给出了一个等价但更高效的准则：ℓ-多项式β的一个S-约化子tβ被称为最小乘性S-约化子，如果

(1)S(tβ)是所有S-约化子中最小的标签；

(2)若有多个S-约化子满足条件1，选取S(β)最大的一个。

事实1 令α∈L*, G为G。对于矩阵型GVW算法，α的S-约化子tβ通过合冲和重写准则当且仅当其是最小乘性S-约化子。

鉴于篇幅，本文给出其证明思路：证明其逆否命题的充分和必要性。

4.3 并行构造Macaulay矩阵

与文献[14]相同的是，子算法SYMBOLIC_ PREPROCESS函数不指定s的选取先后顺序。这样的好处是可以对该函数进行并行化处理。程序使用了Inter TBB (Thread Building Blocks)库来实现这一操作。具体来说，在构造Macaulay矩阵的时候(即把多项式集合写成||×|T|的矩阵，一行代表中的一个多项式，其中列元素记录了该多项式关于T的系数)，本文用多个线程将中不同多项式写成矩阵的行向量，如线程1当前处理的单项式在THM()中，则线程1得到互斥锁，处理完一个单项式后再释放互斥锁。鉴于篇幅，本文省略算法的具体流程。

5 实验数据

本文代码是基于Mathicgb库[24]的C++实现。硬件平台为Intel Core i3 2.40 GHz，运行环境为64-bit Ubuntu 14.04操作系统。基域为F32003，单项式序为≤DRL。为了检验线性代数方法对于Gröbner基算法是否有加速作用，本文对矩阵型和Buchberger型GVW算法进行实验比较。表1～表4中，矩阵型GVW算法使用了≤SR模序，SD(按s-次数排列c-对)，重写序为r。实验显示，线性代数方法对Cyclic系列和Katsura系列多项式系统能加速2～6倍，但该技术不具有普适性。例如GVW算法能在不到2 s的时间内求出Jason210多项式系统的Gröbner基，而矩阵型GVW算法在45 min内都不能算出结果。

表2可以看出矩阵版本需要消耗更多的内存，这是由于把多项式集合V存储成Macaulay矩阵的开销很大，尽管本文已经使用了稀疏矩阵作为其存储结构。

表1 运行时间(s)

表2 内存占用情况 (MB)

除了上节伪代码所描述的矩阵型算法外，本文还实现了基于其它策略或准则的矩阵型算法。例如，表3第3列是使用F5算法的重写准则：选取G中最新的S-约化子。显然，在实现上new比r(第2列)要稍快。实验结果显示，对于Cyclic系列和Eco系列方程组，new比r要差的多。对于Katsura系列多项式系统，new只需要在r下一半的运行时间。这一特殊情况是由于算法关于两个重写序所算出的S-Gröbner基是相同，并且由表4可知r需要更多的约化操作。

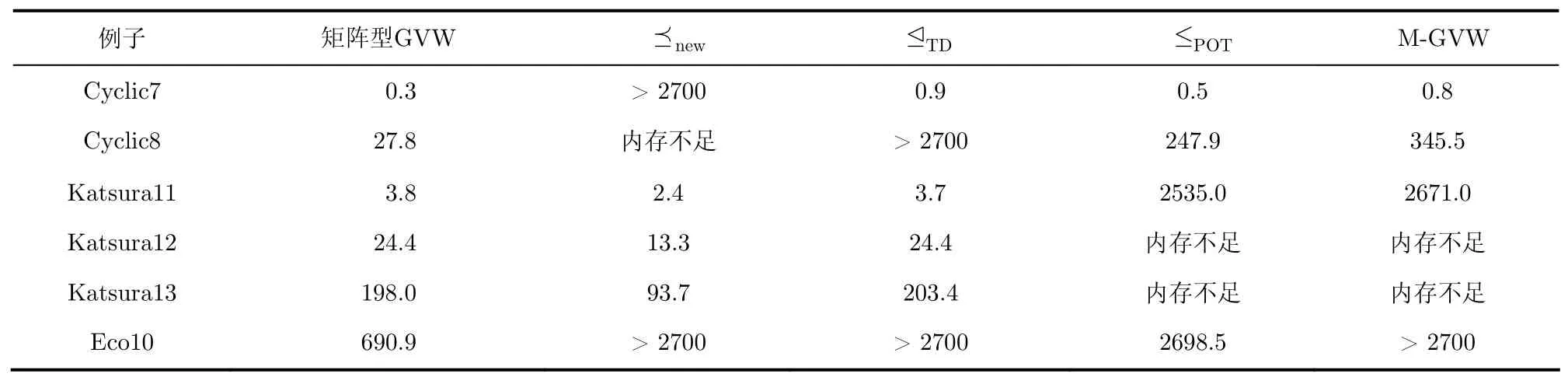
表3 矩阵型算法运行时间(s)

表3第4列表示算法矩阵型GVW按照全次数从小到大的顺序来选取c-对。文献[3]表示，TD对于F4算法比SD要高效。然而，对于基于标签的Gröbner基算法，本文的实验结果说明了这一论断是不成立的。

表3第5列是算法用了模序≤POT而不是≤SR的结果。需要注意的是，在排列c-对时算法仍然使用SD，这样一来，每一个Macaulay矩阵就能包含尽可能多的多项式。表格第6列是文献[14]中的矩阵型M-GVW算法，其模序为≤POT，按TD选取c-对。M-GVW使用了一个新的策略：如果算法计算出一个突变，则将其c-约化后赋以新的标签。也就是说，算法将其看成一个新的输入多项式。这样，新的ℓ-多项式在已算出的G中是关于模序最小的，算法就不会因为其它准则来丢掉与突变相关的c-对。注意，M-GVW只对次数小于某一常数的突变进行处理，而在文献[14]中没有给出这一常数的具体值。所以本文在实现矩阵型M-GVW的时候只对算法找到的第1个突变重赋标签。这样做的目的是确保M-GVW不会像文献[14]所说的那样降低性能，然而运行结果出乎意料：M-GVW计算表3的多项式系统要比≤POT还要差些。从表3可以得出，无论是≤POT还是矩阵型M-GVW，它们在计算Gröbner基的效果上都比矩阵型GVW要差。

综上所述，本文所实例化的矩阵型GVW算法是权衡了各项准则及策略的实现，具有相当的实用性。找到一个对所有多项式系统都行之有效的算法是相当困难的，即使是F4和F5算法也做不到。因此，怎样设计更好更快的Gröbner基算法的研究是值得继续研究的问题。

表4 约化总步数

[1] Buchberger B. Ein algorithmus zum auffinden der basiselemente des restklassenrings nach einem nulldimensionalen polynomideal[D]. [Ph.D. dissertation], Universität Innsbruck, Austria, 1965.

[2] Lazard D. Gröbner-bases, Gaussian elimination and resolution of systems of algebraic equations[C]. Proceedings of the European Computer Algebra Conference on Computer Algebra, London, UK, 1983: 146-156.

[3] Faugère J C. A new efficient algorithm for computing Gröbner bases (F4)[J]. Journal of Pure and Applied Algebra, 1999, 139(1-3): 61-88.

[4] Faugère J C. A new efficient algorithm for computing Gröbner bases without reduction to zero (F5)[C]. Proceedings of the 27th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2002: 75-83.

[5] Faugère J C and Joux A. Algebraic cryptanalysis of hidden field equation (HFE) cryptosystems using Gröbner bases[C]. Proceedings of the Advances in Cryptology-CRYPTO 2003, Springer Berlin Heidelberg, Santa Barbara, USA, 2003, 2729: 44-60.

[6] Bardet M. Étude des systèmes algébriques surdéterminés. applications aux codes correcteurs et à la cryptographie[D]. [Ph.D. dissertation], Université Pierre et Marie Curie-Paris VI, 2004.

[7] Faugère J C and Rahmany S. Solving systems of polynomial equations with symmetries using SAGBI-Gröbner bases[C]. Proceedings of the 34th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2009: 151-158.

[8] Albrecht M and Perry J. F4/5[OL]. http:// adsabs. harvard. edu/abs/2010arXiv1006.4933A. 2010.

[9] Faugère J C, Safey El Din M, and Verron T. On the complexity of computing Gröbner bases for quasihomogeneous systems[C]. Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2013: 189-196.

[10] Bardet M, Faugère J C, and Salvy B. On the complexity of the F5 Gröbner basis algorithm[OL]. http://arxiv.org/abs/ 1312.1655. 2013.

[11] Arri A and Perry J. The F5 criterion revised[J]. Journal of Symbolic Computation, 2011, 46(9): 1017-1029.

[12] Gao Shu-hong, Guan Yin-hua, and Volny F IV. A new incremental algorithm for computing Groebner bases[C]. Proceedings of the 35th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2010: 13-19.

[13] Gao Shu-hong, Volny F, and Wang Ming-sheng. A new algorithm for computing Gröbner bases[OL]. http://www. math.clemson.edu/～sgao/papers/gvw_R130704.pdf. 2010.

[14] Sun Yao, Lin Dong-dai, and Wang Ding-kang. An improvement over the GVW algorithm for inhomogeneous polynomial systems[OL]. http://arxiv.org/abs/1404.1428. 2014.

[15] Huang Lei. A new conception for computing Gröbner basis and its applications[OL]. http://arxiv.org/abs/1012.5425. 2010.

[16] Pan Sen-shan, Hu Yu-pu, and Wang Bao-cang. The termination of the F5 algorithm revisited[C]. Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2013: 291-298.

[17] Eder C. An analysis of inhomogeneous signature-based Gröbner basis computations[J]. Journal of Symbolic Computation, 2013, 59(0): 21-35.

[18] Eder C and Roune B H. Signature rewriting in Gröbner basis computation[C]. Proceedings of the 38th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2013: 331-338.

[19] Ding Jin-tai, Cabarcas D, Schmidt D, et al.. Mutant Gröbner basis algorithm[C]. Proceedings of the 1st International Conference on Symbolic Computation and Cryptography, Beijing, China, 2008: 23-32.

[20] Sun Yao and Wang Ding-kang. A generalized criterion for signature related Gröbner basis algorithms[C]. Proceedings of the 36th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2011: 337-344.

[21] Eder C and Perry J. Signature-based algorithms to compute Gröbner bases[C]. Proceedings of the 36th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2011: 99-106.

[22] Volny F. New algorithms for computing Gröbner bases[D]. [Ph.D. dissertation], Clemson University, 2011.

[23] Greuel G M and Pfister G. A Singular Introduction to Commutative Algebra[M]. New York: Springer Berlin Heidelberg, 2008: 161-162.

[24] Roune B H and Stillman M. Practical Gröbner basis computation[C]. Proceedings of the 37th International Symposium on Symbolic and Algebraic Computation, New York, USA, 2012: 203-210.

潘森杉： 男，1986年生，博士生，研究方向为多变量公钥密码、Gröbner基.

胡予濮： 男，1955年生，博士，博士生导师，教授，研究方向为格公钥密码、流密码等.

王保仓： 男，1979年生，博士，硕士生导师，副教授，研究方向为格公钥密码、多变量密码等.

Research on Signature-based Gröbner Basis Algorithms in Matrix Style

Pan Sen-shan Hu Yu-pu Wang Bao-cang
(State Key Laboratory of Integrated Service Networks, Xidian University, Xi'an 710071, China)

The current signature-based Gröbner basis algorithms are mostly in Buchberger style and the researches related to matrix style often aim to analyze the complexity of algorithms. From a practical aspect, this paper provides a concrete Gao-Volny-Wang (GVW) algorithm in matrix style and presents optimization at the algorithmic level. Meanwhile, an efficient reduction criterion is given in the paper. Many popular criteria and strategies are compared by some experiments which show that the matrix version described in the paper is a combination of reasonable criteria and strategies. Moreover, the matrix-GVW is two to six times faster than the Buchberger style for some polynomial systems, e.g. Cyclic series and Katsura series.

Cryptography; Gröbner basis; Signature; Polynomial; Gao-Volny-Wang (GVW) algorithm

TP309

： A

：1009-5896(2015)04-0881-06

10.11999/JEIT140831

2014-06-23收到，2014-11-02改回

国家自然科学基金(61173151, 61173152)资助课题

*通信作者：潘森杉 pansenshan@gmail.com