脉间Costas跳频脉内多载波混沌相位编码雷达信号设计与分析

黄琼丹李 勇*卢光跃

①(西北工业大学电子信息学院 西安 710072)

②(西安邮电大学通信与信息工程学院 西安 710112)

脉间Costas跳频脉内多载波混沌相位编码雷达信号设计与分析

黄琼丹①李 勇*①卢光跃②

①(西北工业大学电子信息学院 西安 710072)

②(西安邮电大学通信与信息工程学院 西安 710112)

该文在步进频信号的基础上，把基于混沌调制的多载波相位编码(Multi-Carrier Phase Coded, MCPC)信号作为子脉冲，用Costas跳频代替频率的线性步进，设计出脉间Costas跳频脉内多载波混沌相位编码(Inter-Pulse Costas frequency hopping and intra-pulse Multi-Carrier Chaotic Phase Coded, IPC-MCCPC)雷达信号，并对其模糊函数及自相关性能进行了研究。仿真分析表明，该文设计的信号继承了步进频信号用较小的瞬时带宽合成较大的工作带宽的优点，同时有效克服了步进频信号存在的距离-速度耦合的缺点。脉内多载波特性使得这种信号在保持总带宽和步进频信号相等的条件下减少跳频阶数，从而提高信号处理的数据率；混沌调相的引入使得这种信号具有更强的保密性；脉间频率的随机跳变使其模糊函数具有更低的周期性旁瓣。这种信号众多的参数、灵活的结构及较大的调制复杂度，增加了侦察接收机匹配和识别的难度，从而提高雷达的反截获性能。

雷达；混沌；Costas；多载波相位编码；模糊函数

1 引言

雷达波形设计是雷达总体设计的主要内容之一[1,2]，是提高雷达系统低截获性能的关键技术[3,4]。文献[5]提出多载波相位编码(MCPC)信号通过同时发射多个彼此正交的相位编码载波，使其具有图钉型模糊函数，宽带和窄带性能在MCPC信号中得到了较好的结合，且其调制解调简单，可以实现快速处理[6−8]。作为一种重要的宽带雷达信号，步进频脉冲串信号的子脉冲频率呈线性规律递增[9]，由于具有较窄的瞬时带宽，可以在窄带发射机、接收机的条件下工作，从而降低对数字信号处理机瞬时带宽的要求，而且通过对脉冲回波的离散傅里叶反变换(Inverse Discrete Fourier Transform, IDFT)可获得距离高分辨率的效果[10]。但步进频信号存在较严重的距离-速度耦合，增加了速度补偿的难度[11]。文献[12]结合了MCPC及频率步进信号的特点，设计了多载波相位编码频率步进雷达脉冲串信号，这种信号有较高的距离分辨力，距离-速度耦合现象影响了运动目标的距离-速度分辨率。而且，步进频波形在进行目标探测时存在距离分辨率和距离模糊旁瓣值之间的矛盾，如果采用一些性能优良的频率编码方式来代替频率的线性变化就能很好地克服上述缺点[13]。

为加大雷达信号脉内及脉间的随机性，本文在步进频信号的基础上，脉间采用Costas跳频形式，脉内采用混沌相位编码的多载波形式，设计出脉间Costas跳频脉内多载波混沌相位编码(Inter-Pulse Costas frequency hopping and intra-pulse Multi-Carrier Chaotic Phase Coded, IPC-MCCPC)信号，推导并分析了这种信号的模糊函数，并对其自相关性能进行了研究。

2 Costas阵列的构造

Costas跳频信号[14,15]每个脉冲的频率随机出现并仅出现一次，而且模糊函数非原点处(τ≠0或v≠0，其中v代表多普勒频移，τ代表时延)的最大值为1。假设一个Q×P的矩阵C,C的每一行(q= 1,2,…,Q)代表频率q,C的每一列(p=1,2,…,P )代表第p个脉冲，P为脉冲个数，也叫步进阶数。基于有限域理论的Costas阵列Welch构造法[16]如图1所示。

以g=11为例，对应的Costas跳频如图2(a)所示，图2(b)是步进频频率分布。模糊函数可近似看成复制图2所示的频率分布在原图上进行时间轴和频率轴的移位时频率分布点(图示黑点)重叠个数总和[6]。图2(a)及图2 (b)对应的模糊函数局部示意图(vmax=τmax=5)如图3所示。从图3可知，步进频信号由于频率的线性变化，使得模糊函数存在明显的“斜脊”，且能量集中在原点(τ=v=0)附近，造成了较为严重的距离-多普勒耦合，而Costas信号由于脉间的频率变化满足Costas阵列规律，其模糊函数最大副瓣为1，能量较为均匀地分布在除了原点之外的整个距离-多普勒平面，不存在明显的“斜脊”，克服了步进频信号固有的缺陷。

3 脉间Costas跳频脉内多载波混沌相位编码雷达信号设计

3.1 单周期MCPC信号

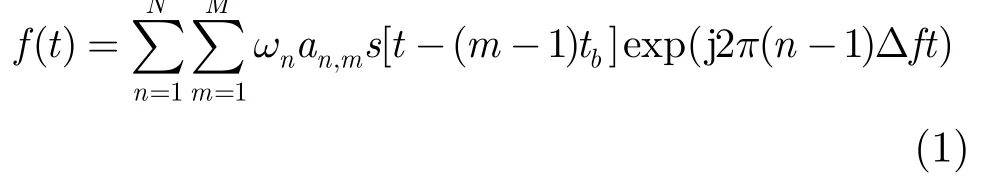
单周期MCPC信号的复包络f(t)的表达式为其中，N为子载波个数，M为每个子载波的码元个数，an,m=ejϕn,m为第n个子载波中的第m个码元的相位编码，ϕn,m为第n个子载波中的第m个码元的相位。且, tb为码元时宽，Δf为载波间隔。对于OFDM信号，载波间隔取为子载波带宽可以最小限度地保证各个载波之间的正交性[6]。MCPC信号在OFDM的基础上对每条载波进行了相位调制，各个子载波上的带宽为码元持续时间tb的倒数，同理，令Δf=1/tb，可以最小限度地保证MCPC信号各载波之间的正交性。ωn

n加权相位。

3.2 脉间Costas跳频脉内多载波混沌相位编码信号

脉间Costas跳频脉内多载波混沌相位编码信号的复包络表达式为

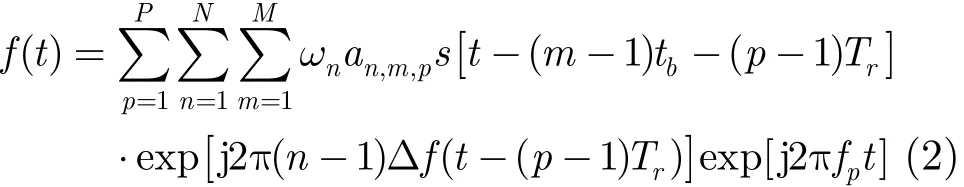
其中，P为步进阶数，Tr为脉冲重复周期，an,m,p=ejϕn,m,p和ϕ分别为第p个脉冲的第n个载波上

n,m,p的第m个码元基于某种混沌映射的混沌相位编码及相位，fp=f0+(Cp−1)B ,f0为发射的基准频率，B=NΔf为单个脉冲MCPC信号的带宽，Cp为Costas序列。其余参数和单脉冲MCPC信号参数相同。从式(2)可以看出，IPC-MCCPC信号的每个脉冲的频率以跳频间隔B按Costas阵列排列，即相邻的脉冲频率步进量为单脉冲MCPC信号带宽B的整数倍。

图1 Costas阵列的Welch构造法

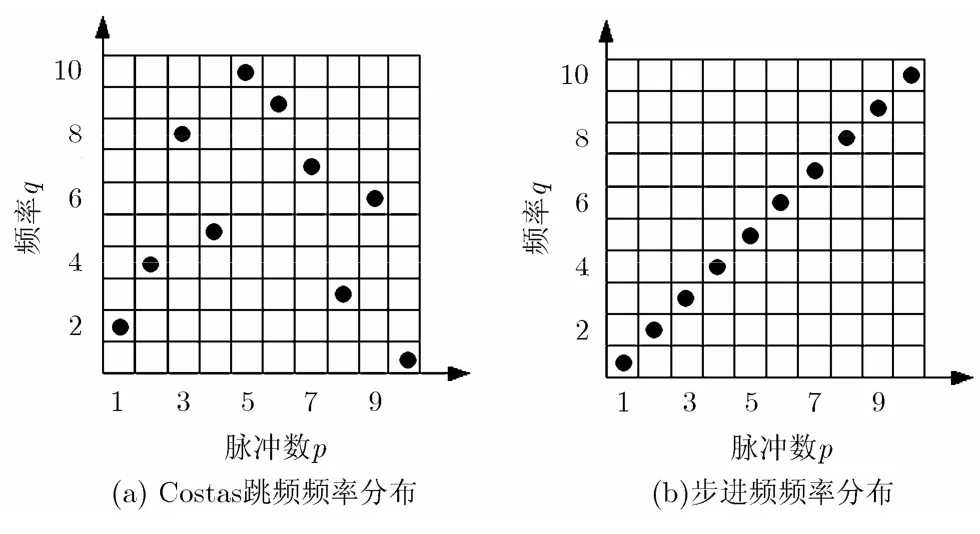
图2 Costas及步进频脉冲串频率分布图

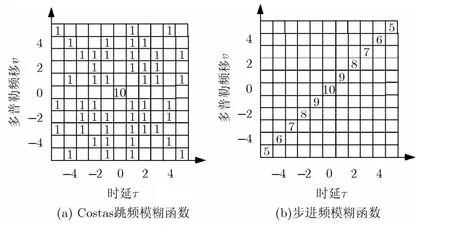
图3 Costas及步进频模糊函数局部示意图

混沌调制的雷达信号具有较高的距离速度分辨力、图钉型的模糊函数、良好的抗干扰能力[17,18]。式(2)中的an,m,p=ejϕn,m,p由改进型Logistic混沌映射产生。改进型Logistic映射的数学表达式为

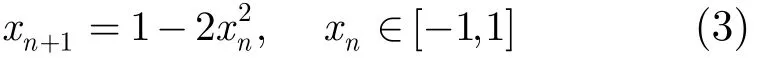
产生L=P×N×M 个混沌二相码，表示为集合形式：{x1,x2,…,xL}，按式(4)对式(2)各载波进行调相：

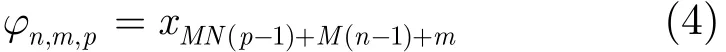
得到IPC-MCCPC信号，其结构如图4所示(以P=10,N=M=5为例)。

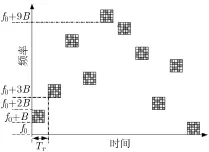
图4 IPC-MCCPC信号结构示意图

将式(2)代入式(5)，并交换求和与积分的次序，得到IPC-MCCPC信号的模糊函数：

3.3 模糊函数推导

模糊函数是分析雷达信号的重要工具，信号f(t)的模糊函数χ(τ,v)定义为[6]

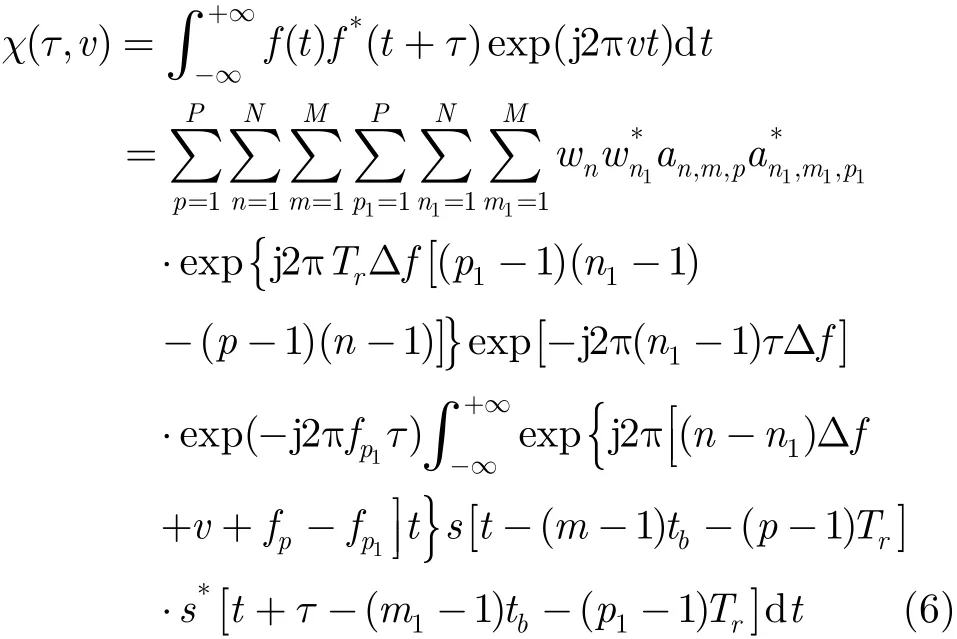
∵fp=f0+(Cp−1)B,fp1=f0+(Cp1−1)B ，式(6)可以化简为

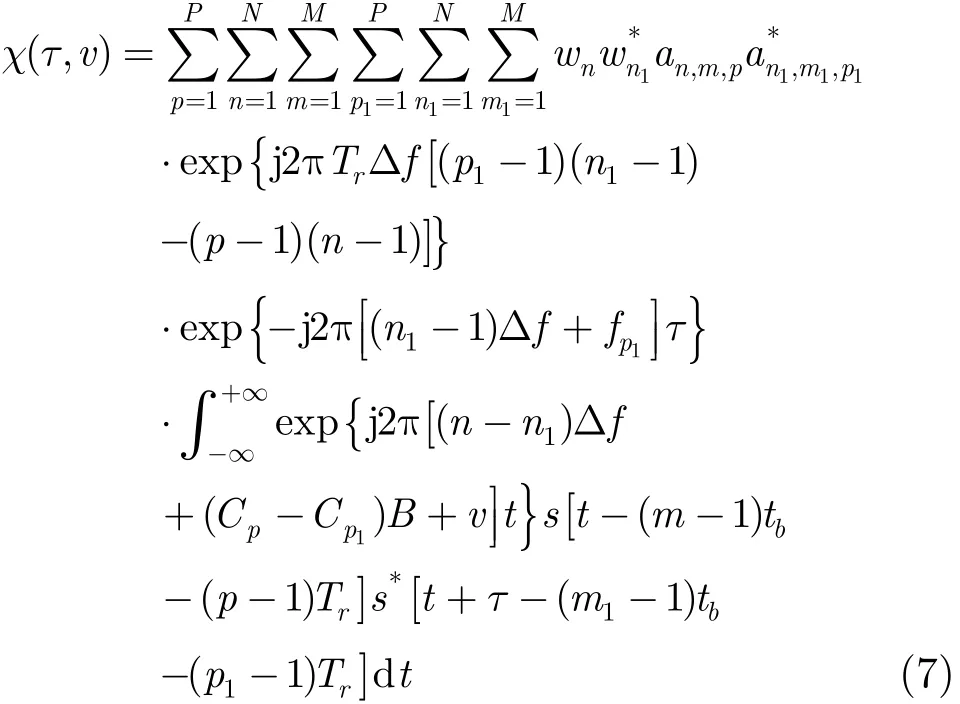
令(n−n1)Δf+(Cp−Cp1)B+v=Fd,t−(m−1)tb−(p−1)Tr=t'，式(7)中的积分可以化简为

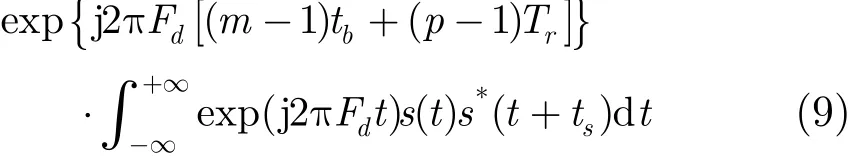
若ts≥0，式(9)的积分为

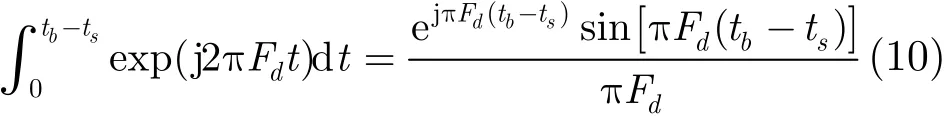
若ts＜0，式(9)的积分为

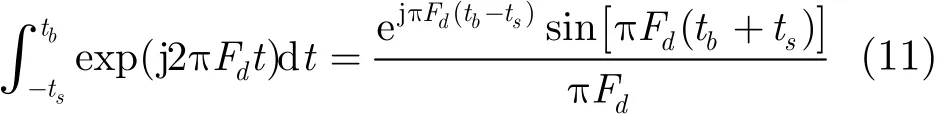
综合式(10)和式(11)，式(9)的积分结果为

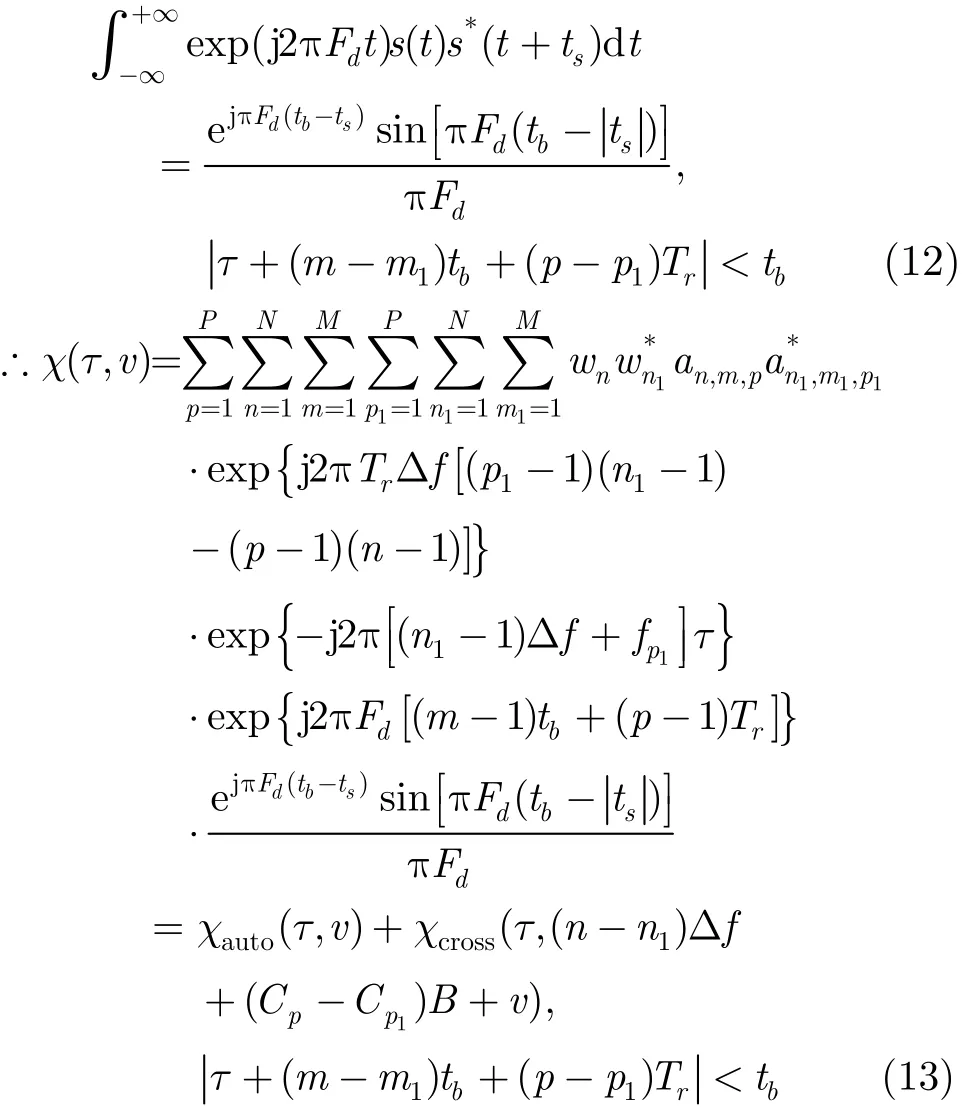
其中

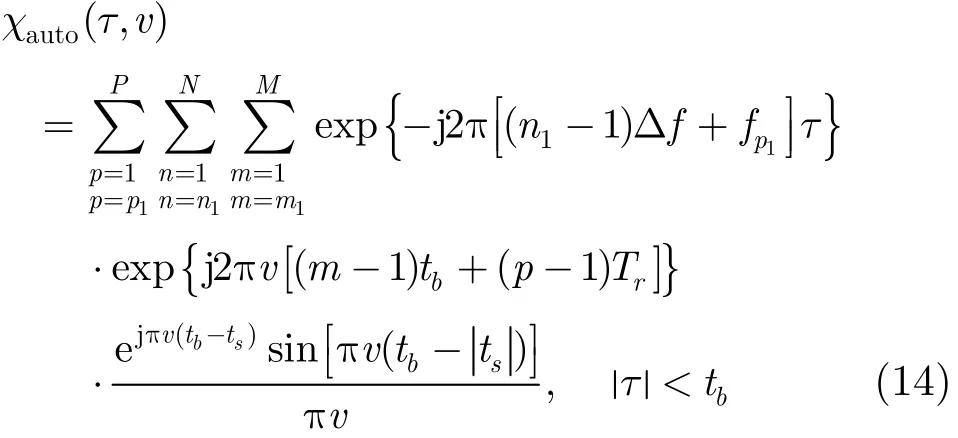
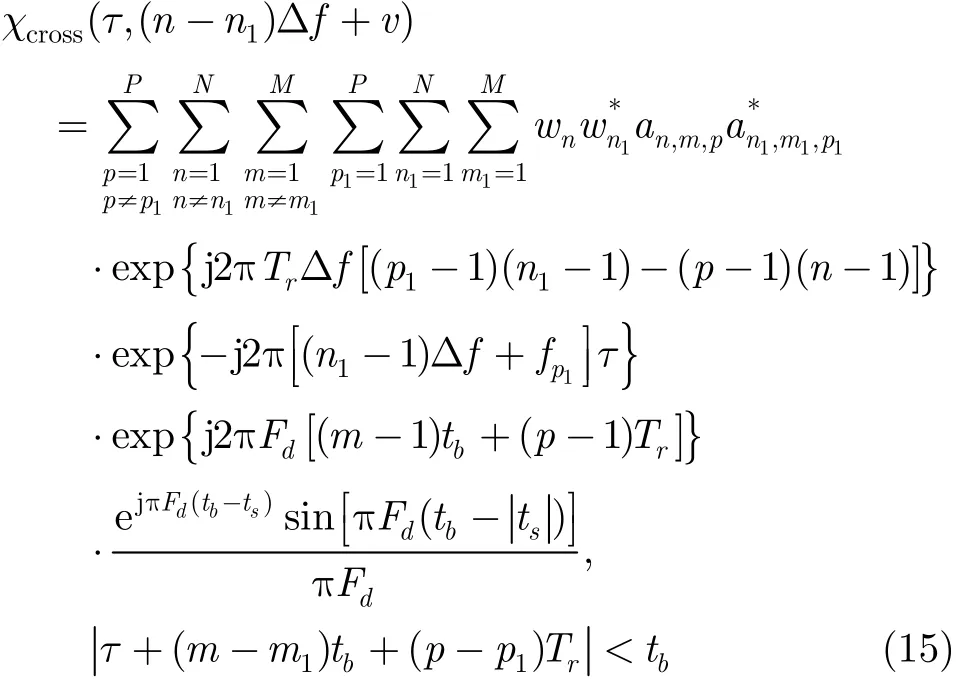
为IPC-MCCPC的自模糊函数，是模糊函数的主要部分。为IPC-MCCPC的互模糊函数，属于邻道干扰，对模糊函数的贡献较小。

4 仿真结果分析

把IPC-MCCPC信号、脉间步进频脉内多载波混沌相位编码(Inter-Pulse Stepped frequency and intra-pulse Multi-Carrier Chaotic Phase Coded, IPS-MCCPC)信号和把IPS-MCCPC的多载波改成单载波得到的脉间步进频脉内混沌相位编码(Inter-Pulse Stepped frequency and intra-pulse Chaotic Phase Coded, IPS-CPC)信号的自相关性能和模糊函数进行对比。3种信号的基本参数相同，设为：P=6,N=7,M =13,tb=10−6s ，脉宽T=M ×10−6s,=1(不加窗)。

4.1 自相关性能分析

混沌序列不同的初值导致信号不同的自相关性能。图5给出了初值以0.001的步长从-1到+1时对应的自相关峰值旁瓣水平(Peak Side-Lobe Level, PSLL)。从图5可以看出，IPS-CPC信号用到的混沌序列长度为其它两种信号的1/N，其自相关性能较差，原因在于混沌序列长度越短，自相关性能越差。

把最小PSLL对应的初值称为最优初值。设最优初值对应的最小PSLL为Pmin, IPS-CPC, IPSMCCPC及IPC-MCCPC 3种信号的Pmin分别为-16.811 dB, -24.983 dB及-25.339 dB, 3种信号在指定的PSLL条件下对应的混沌初值个数如表1所示。从表1可以看出，在PSLL相差不大的情况下，有多个混沌初值对应的信号具有相似的自相关性能。而混沌信号是对初值敏感的，可以通过改变混沌映射初值来发射时域波形不同但自相关性能相差不大的雷达波形，操作简单，同时又增加了侦察接收机截获及识别的难度。

由图6 3种信号的自相关可看出IPS-MCCPC及IPC-MCCPC的自相关性能优于IPS-CPC。

4.2 模糊函数分析

图7(a), 7(b)及7(c)分别为最优初值条件下IPSCPC, IPS-MCCPC及 IPC-MCCPC的模糊函数。图8(a), 8(b)及8(c)分别为3种信号的模糊函数时延轴(τ)在3个码元时间内的放大显示图。

图5 混沌初值对3种信号PSLL的影响

表1 3种信号在给定PSLL条件下对应的混沌初值个数

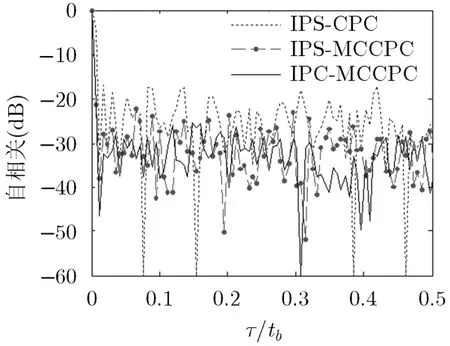
图6 最优初值条件下3种信号的自相关

由图7及图8可看出，IPS-CPC的模糊函数呈现倾斜刀刃型，存在较大程度的距离-速度耦合，IPS- MCCPC由于频率仍然是线性步进，距离-速度的耦合依然存在，但由于脉内载波数增加，混沌调相序列变长，随机性加大，这种耦合比IPS-CPC小。IPC-MCCPC脉间的随机性加大，具有图钉型的模糊函数，且其Tr整数倍上的周期性旁瓣比IPSMCCPC的周期性旁瓣低。IPS-MCCPC及IPCMCCPC信号由于引入了脉内的多载波，带宽得到展宽，故在ν=0切面上的主瓣更为尖窄。

图9给出了令τ=0和τ=τ0=1/fs时的多普勒模糊图。从图9(a)可知，由于积累周期一样，3种信号的多普勒分辨率相同。相关积累会因为目标的运动而不能获得最大输出信噪比，把相关积累输出的幅度降低到最大值的δ倍时，对应的多普勒频率称为多普勒容限。大多普勒容限有利于目标的搜索及高速目标的跟踪。在这里，假设δ=0.707，即相关积累输出下降了3 dB，设此时对应的多普勒容限为νd，可以通过式(16)计算出多普勒容限速度νT，其中信号载波为fc，光速为c。

从图9(b)可以看出，IPS-CPC由于存在距离-速度耦合，当时延τ0时，存在模糊峰，导致目标速度和距离均未知时，两者均测不准，而且对于斜脊附近的多目标无法分辨。IPS-MCCPC虽然比IPS-CPC的模糊峰低，但是由于频率的线性步进，还是存在一定模糊峰，距离-速度联合分辨率不高，而IPC- MCCPC信号由于脉间的随机变化，不存在距离-速度的耦合。

4.3 IPC-MCCPC雷达波形参数设计

IPC-MCCPC众多的参数对雷达系统性能的影响是相互制约的，要根据实际情况综合考虑。载波间隔Δf应取为码元持续时间tb的倒数以保证各个载波之间的正交性。增加tb和码元数目M可以增加信号的发射能量，但tb增加会导致信号带宽变小，从而影响距离分辨率。步进阶数P须满足Costas编码条件，即P+1要求为奇素数。P和N越大距离分辨率越高，但P和N增大都会导致多普勒容限的降低[19]。N,M及P的增加使得混沌二相码长度更长，有利于改善信号的自相关性能，并增加敌方截获的难度。但P越大，系统将耗费更多时间等待脉冲串的收发以完成信号处理，从而降低数据率。为了提高数据率，又必须减小P，而P减小导致系统带宽减小，进而导致分辨率降低。若要保证带宽不变，P减小了，时宽就要降低以保证带宽的不变，这时雷达的作用距离就降低了。所以，周期数、时宽及带宽是相互制约的关系。尽管如此，IPSMCCPC及IPC-MCCPC信号由于脉内引入了多载波，其跳频间隔为IPS-CPC的N倍，故可以在保持带宽和IPS-CPC一样的情况下降低跳频点数，提高数据率。

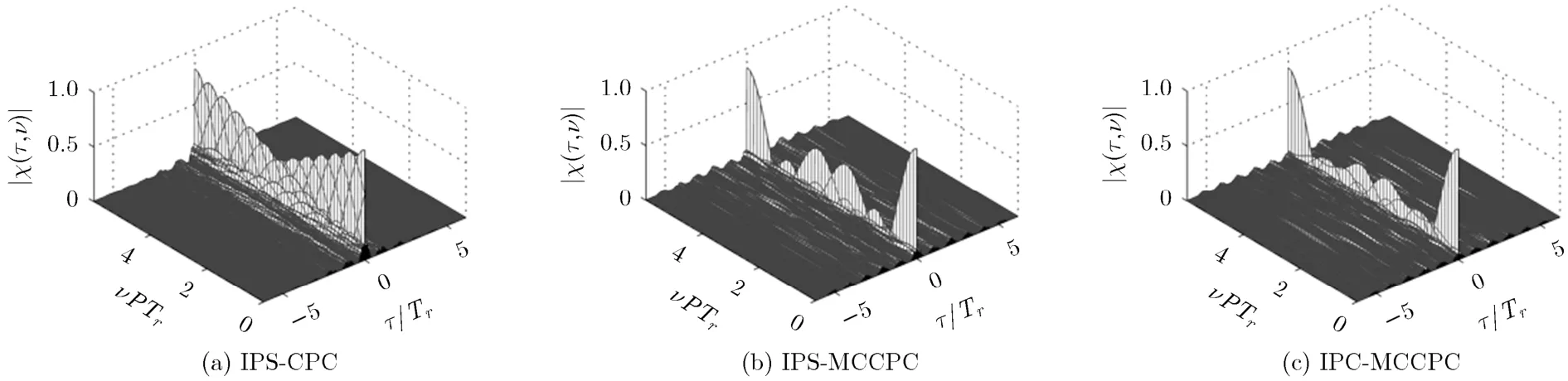
图7 3种信号的模糊函数

图8 3种信号模糊函数的放大显示

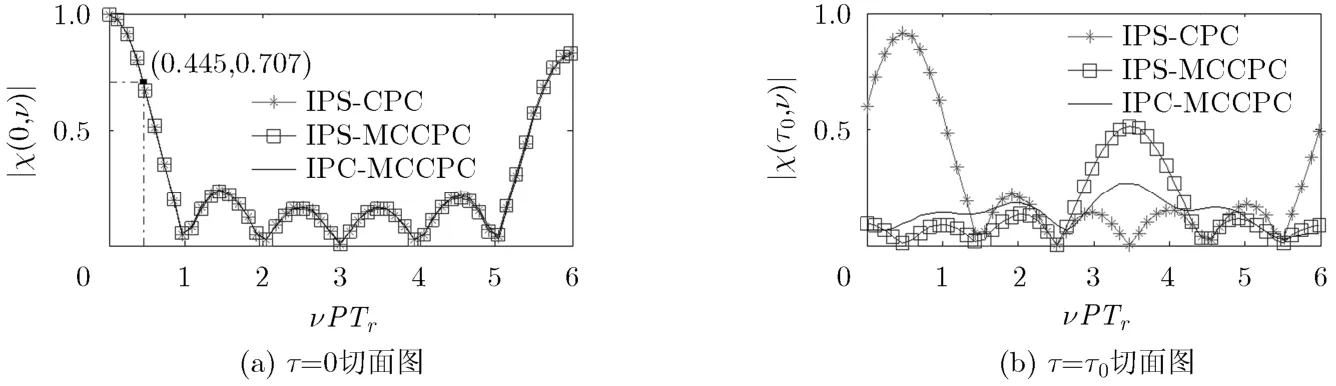
图9 多普勒模糊图

5 结束语

本文设计的IPC-MCCPC信号具有“图钉型”的模糊函数，优良的自相关性质，较高的距离速度分辨力。而且较好自相关性能的IPC-MCCPC信号有不同的混沌初值与之对应，可以通过简单的改变混沌初值获得性能相似但波形不同的信号，有利于波形分集。而且由于脉内多载波的引入可以保持带宽和步进频信号一样的情况下降低步进阶数，从而降低数据率。总之，该信号复杂且灵活的结构及类噪声特性使得侦察接收机很难截获并分析出信号的特性，从而提高了雷达系统反截获的性能。

[1] Piezzo M, De Maio A, Aubry A, et al.. Cognitive radar waveform design for spectral coexistence[C]. Proceedings of the 2013 IEEE Radar Conference (RADAR), Ottawa, Canada, 2013: 1-4.

[2] Wang L, Fu X, Shi L, et al.. Radar waveform design under the constraint of auto-correlation, orthogonality and Doppler tolerance[C]. Proceedings of the IET International Radar Conference, Xi'an, China, 2013: 1-4.

[3] Stove A G, Hume A L, and Baker C J. Low probability of intercept radar strategies[J]. IEE Proceedings-Radar, Sonar and Navigation, 2004, 151(5): 249-264.

[4] 张锡熊. 低截获概率(LPI)雷达的发展[J]. 现代雷达, 2003, 25(12): 1-4.

Zhang Xi-xiong. Development of LPI radar[J]. Modern Radar, 2003, 25(12): 1-4.

[5] Levanon N. Multifrequency complementary phase-coded radar signal [J]. IEE Proceeding-Radar, Sonar and Navigation, 2000, 147(6): 276-284.

[6] Levanon N and Mozeson E. Radar Signals [M]. New York, John Wiley & Sons, 2004: 74-95.

[7] 邓斌. 多载频相位编码雷达信号设计与处理技术研究[D]. [博士论文], 国防科技大学, 2011: 53-64.

Deng Bin. Research on the signal designing and processing of multi-carrier phase coded radar[D]. [Ph.D. dissertation], National University of Defense Technology, 2011: 53-64.

[8] Lellouch G and Mishra A K. Multi-carrier based radar signal optimization using genetic algorithm[C]. Proceedings of the Third International Conference on Soft Computing for Problem Solving, Greater Noida, India, 2014: 525-534.

[9] Levanon N. Stepped-frequency pulse-train radar signal[J]. IEE Proceedings-Radar, Sonar and Navigation, 2002, 149(6): 297-309.

[10] Liu Yi-min, Huang Tiao-yao, Meng Hua-dong, et al.. Fundamental limits of HRR profiling and velocity compensation for stepped-frequency waveforms[J]. IEEE Transactions on Signal Processing, 2014, 62(17): 4490-4504. [11] Gill G S. Step frequency waveform design and processing for detection of moving targets in clutter[C]. Proceedings of the IEEE 1995 International Radar Conference, Alexandria, Egypt, 1995: 573-578.

[12] 霍凯, 姜卫东, 黎湘, 等. 一种新的OFDM相位编码频率步进雷达信号及其特性[J]. 电子与信息学报, 2011, 33(3): 677-683.

Huo Kai, Jiang Wei-dong, Li Xiang, et al.. A new OFDMphase-coded stepped-frequency radar signal and its characteristic[J]. Journal of Electronics & Information Technology, 2011, 33(3): 677-683.

[13] Taylor K, Rickard S, and Drakakis K. Costas arrays, number of hops, and time-bandwidth product[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1995-2004.

[14] Yue L, Run W, Yongping H, et al.. Super-resolution imaging realization of costas signal[J]. TELKOMNIKA Indonesian Journal of Electrical Engineering, 2014, 12(2): 1374-1384.

[15] Huang Jen-fa, Yang Chao-chin, and Huang Chun-ming. On analyzing quasi-cyclic LDPC codes over modified welchcostas-coded optical CDMA sysytem[J]. IEEE Journal of Light Wave Technology, 2009, 27(12): 2150-2158.

[16] Mahafza B R and Elsherbeni A Z. MATLAB Simulations for Radar Systems Design [M]. London, Chapman & Hall, 2003: 202-212.

[17] Boccaletti S, Grebogi C, Lai Y C, et al.. The control of chaos: theory and application [J]. Physics Reports, 2000(329): 103-197.

[18] Carroll T L. Adaptive chaotic maps for identification of complex targets[J]. IET Radar, Sonar & Navigation, 2008, 2(4): 256-262.

[19] Franken G E A, Hikookar H, and van Genderen P. Doppler tolerance of OFDM-coded radar signals[C]. Proceedings of the 3rd European Radar Conference (EuRAD 2006), Manchester, UK, 2006: 108-111.

黄琼丹： 女，1979年生，副教授，博士生，研究方向为雷达信号设计及处理.

李 勇： 男，1962年生，博士，教授，博士生导师，研究方向为信号及信息处理.

卢光跃： 男，1971年生，博士，教授，博士生导师，研究方向为通信及信息处理.

Design and Analysis of Inter-pulse Costas Frequency Hopping and Intra-pulse Multi-carrier Chaotic Phase Coded Radar Signal

Huang Qiong-dan①Li Yong①Lu Guang-yue②

①(School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China)

②(School of Telecommunication and Information Engineering, Xi'an University of Post & Telecommunications, Xi'an 710112, China)

Through taking the Multi-Carrier Phase Coded (MCPC) signal as the subpulse, and replacing the linear frequency step with the Costas frequency hopping, a new Inter-Pulse Costas frequency hopping and intra-pulse Multi-Carrier Chaotic Phase Coded (denoted by IPC-MCCPC) radar signal is designed on the basis of stepped-frequency signal. The ambiguity function and autocorrelation performance of the designed signal are studied. Simulation results show that the designed signal carries forward the advantage that the stepped-frequency signal achieves a larger operating bandwidth by instantaneous bandwidth synthesis, and overcomes the defect of range-velocity coupling caused by frequency-stepped. The interpulse's multi-carrier characteristic can decrease the frequency stepped pulse number under the condition of keeping the total bandwidth as same as the stepped-frequency signal, thus increases the data rate of signal processing. The designed signal has stronger secrecy due to the introduction of chaotic phase modulation. The ambiguity function of designed signal has lower periodic side lobe because the Costas frequency hopping. Besides that, the designed signal has flexible structure, numerous parameters and complex modulation mode makes it more difficult to be identified by reconnaissance receivers, so the anti-intercept ability of radar system is greatly improved.

Radar; Chaotic; Costas; Multi-Carrier Phase Coded (MCPC); Ambiguity function

TN957

： A

：1009-5896(2015)06-1483-07

10.11999/JEIT140653

2014-05-19收到，2015-01-29改回

航空科学基金(20112053018)资助课题

*通信作者：李勇 ruikel@nwpu.edu.cn