基于虚拟平面的米波组网雷达测高算法
2015-07-12添沈一鹰刘永坦
夏 添沈一鹰 刘永坦 陈 迪
(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)
基于虚拟平面的米波组网雷达测高算法
夏 添*沈一鹰 刘永坦 陈 迪
(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)
随着反隐身技术的发展,米波雷达凭借其反隐身、反辐射导弹方面的天然优势,再度进入科学界的视野。但米波雷达在探测低仰角目标过程中受多路径效应影响严重,导致测高结果易出现较大偏差,无法满足实际需要。而组网雷达数据融合技术的发展为此问题找到了一个解决办法。该文采用组网雷达数据融合技术,仅利用米波雷达测得的距离和方位信息实现了目标的3维定位,从而解决米波雷达测高困难的问题。考虑地球曲率的影响。该文所提出的米波组网雷达测高算法利用大地坐标变换、坐标系变换和数据变换,把各雷达数据统一到一个合理的工作平台,即虚拟平面上,在该平面上对目标进行测高计算。对极小误差法加以改进,采用分辨率不高,但数据稳定性好的方位角信息确定算法的搜索范围;应用分辨率较高的目标距离信息来获取最终的目标经度、纬度、海拔高度估值。由于地面强反射的原因,目标的距离估值有些时候是不准确的,该文设立了置信度判决准则以验证定位的有效性。通过仿真验证,该算法具有较好的测高精度,可作为组网雷达行之有效的测高方法。
米波雷达;组网雷达;高度测量;虚拟平面;极小误差法
1 引言
米波雷达的工作频段在甚高频(VHF),频率范围在30~300 MHz。它是20世纪30年代发明和使用的主要防空雷达,大多数早期雷达都工作在该频段。在雷达使用早期,米波雷达在军事上有着十分重要的意义。但随着科学的发展,对雷达测量精度要求的逐渐提高,微波雷达凭借其定位精度高的优势迅速发展,而米波雷达技术却停滞不前。随着现代飞行器、导弹的发展,隐身技术的出现使各国的防空雷达系统受到严重威胁。米波雷达由于其波长较长,现代隐身技术对其没有效果,因此它又重新进入科学界的视野。然而,米波雷达的测量距离一般在百公里以上,测量目标相对于米波雷达都是低仰角目标。由于其波长较长,在相同天线口径下,其波瓣宽度受到很大的限制,当它在进行低仰角测高时,会产生多路径效应,严重影响了米波雷达的测高精度。很多文献根据雷达波低仰角下复杂地形反射特性[1],提出适用于多径情况下的波达方向估计算法,由仰角计算得到的目标高度量测。这其中的算法大体可以总结为两类:波瓣分裂法[2,3]和超分辨法[4−7]。由单站米波雷达提供的测高精度并不令人满意,难以达到实际使用的需求标准。
组网雷达数据融合技术是对分散在不同位置、覆盖范围相互交叠的多部雷达信息进行实时处理,凭借众多的雷达测量参数来有效地提高测量精度,实现目标较为精确的定位。本文将采用组网雷达数据融合技术,利用米波雷达的距离和方位测量信息实现目标的高度信息获取,从而在一定程度上解决单站米波雷达受多路径效应影响而无法测高的缺点。文献[8]提出了子集优化法,即目标位置由定位精度最好的那组量测子集来决定。这虽然简化了定位优化的计算,但是子集优化法定位精度不高,还可能出现定位模糊的问题。文献[9]提出两种优化算法实现组网雷达定位:最小二乘迭代方法和极小化误差法。最小二乘迭代方法计算量很大,在各量测子集间相关性很弱的条件下是适用的,当相关性不容忽视时,需另行设法采用别的优化算法。极小化误差法经误差标准化后,不同类型的数据可以一起处理,更适合多样数据类型的组网雷达进行数据融合。本文对极小化误差法加以改进使其具有更好的计算性能和稳定性。
为计算简便,绝大多数的雷达数据融合方法忽略了地球曲率的影响,而把地球看作一个平面,由于地球是一个椭球体,并且米波雷达的作用距离较远,通常达到上百公里,此时地球曲率引入的高度差已经不可忽略,故不能用简单的平面三角形关系来计算目标高度,而应当考虑地球曲率的影响。为此,本文首先将3个子坐标系的雷达站址大地坐标(纬度,经度,海拔高度)数据转换到统一的地球坐标系,在地球坐标系上,利用3雷达的站址坐标确定一个搜索虚拟平面。再把3雷达站址地球坐标和子坐标量测数据转换到该虚拟平面上。本文对极小化误差法加以改进,采用分辨率不高,但数据稳定性好的方位角信息确定算法的搜索范围。应用分辨率较高的目标距离信息来获取最终的目标高度估值,该算法具有更好的计算性能和稳定性。所得目标坐标值再经过坐标转换到地球坐标系。由于地面强反射的原因,目标的距离估值有些时候是不准确的,本文设立了置信度判决准则验证定位的有效性。最后经过大地坐标转换从而得到目标的经度,纬度,高度。通过仿真分析研究算法的适用性、可行性、适用范围,讨论不同因素对高度估值的影响。
2 虚拟平面的建立
考虑地球曲率的影响,本文所提出的米波组网雷达测高算法首先利用大地坐标变换,坐标系变换,数据变换,把各雷达数据统一到一个合理的工作平台上,即一个虚拟平面上。算法首先将3个雷达站址的大地坐标数据转换成统一的地球坐标,在地球坐标系上,利用3雷达的站址坐标建立虚拟平面。通过坐标转换和数据转换,把3雷达站址地球坐标和子坐标量测数据转换到该虚拟平面上。
2.1 大地坐标转换
在组网雷达中,各基站所得到的数据需要一个统一的、通用的表达。本文采用WGS-84坐标系(World Geodetic System-1984 coordinate system)。讨论空间直角坐标(x,y,z)和大地坐标(纬度B,经度L,海拔高度H )之间的相互换算问题,由大地测量学可知,空间直角坐标(x,y,z)和大地坐标(B,L,H)有关系。
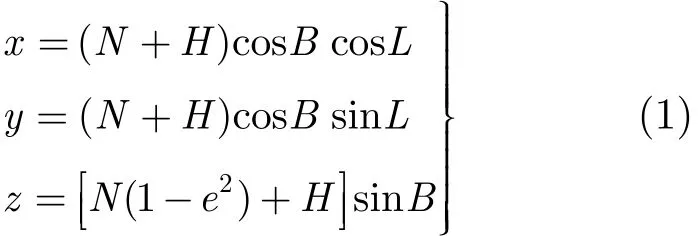
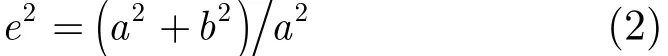
a为地球长半轴,b为地球短半轴。WGS-84中a= 6378137±2 m, e为0.0066943799013。
N为卯酉圈曲率半径,
式中,e为地球椭球第1偏心率。
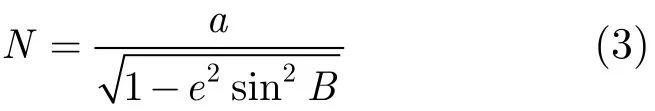
通过式(3)即可把3雷达站址的大地坐标(Bi,Li, Hi)(i=1,2,3)换算为空间直角坐标(xi,yi,zi)。当本文算法得到目标T精确位置信息(xT,yT,zT)时,还需将其换算到大地坐标(BT,LT,HT),以此得到精确的海拔高度。对于由空间直角坐标换算大地坐标的反解问题,要用逐次趋近的方法,按式(4)加以解算:
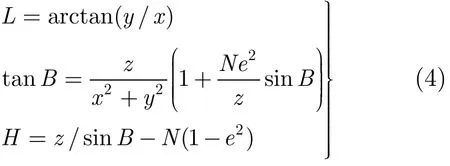
按式(4)做4~5次迭代运算,即可把空间直角坐标(x,y,z)换算为大地坐标(B,L,H)[10,11]。
2.2 确定虚拟平面和坐标系
在组网雷达中,各基站分布在地球不同的经度、纬度、高度上,它们所得到目标的距离、方位角等测量信息是在各站子坐标系中获得的。如图1所示,X, Y, Z为大地坐标系的坐标轴,O1, O2, O3分别代表3部雷达站址,T代表目标。以O1雷达为例,其子坐标系的Z轴方向Z1为OO1方向;X轴方向向量X1, Y轴方向向量Y1在过点O1且垂直于OO1方向向量的平面内,由于Y1轴指向正北方向,所以与O1点经线相切。X1由右手螺旋定则决定。
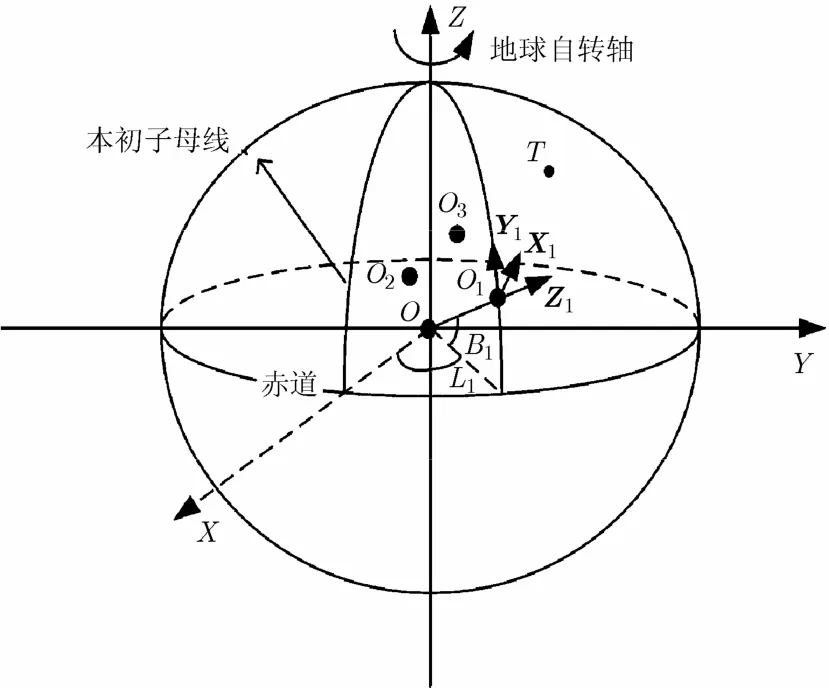
图1 地球坐标系与子坐标系之间的关系
通过式(1)即可把3雷达站址的大地坐标(Bi,Li, Hi)(i=1,2,3)换算为空间直角坐标(xi,yi,zi),已知不共线的3雷达站O1(x1,y1,z1), O2(x2,y2,z2), O3(x3,y3,z3)可确定1个平面O4,本文利用该平面作为虚拟平面,笔者认为在其上进行数据处理最为合理。O4的方程可由Cramer法则求解。设求解后的虚拟平面O4的方程为x+A4y+B4z+C4=0。在该平面上确定原点和正方向。为了简化后续处理,将3站址按经度大小排序,重命名中间点为O1,经度较大点为O2,经度较小点为O3。设经度在中间的雷达坐标点O1点为平面O4的原点。其Y4轴在虚拟平面O4上仍指向正北方向。Z4为平面O4的法线向量(1, A4, B4)。X4轴由右手螺旋定则决定。
2.3 数据转换
因为两坐标雷达只能得到目标距离R和方向角θ。R在任何坐标系下都是两点直线间的距离,数值是不变的,因此只需要将雷达测得的θ转变到虚拟平面O4上。这其中要分两个步骤进行转换:首先是由于雷达所处在不同的经度、维度上,各雷达Y轴方向,即正北方向所指向的方向是不统一的。需要校正北方向带来的角度误差。然后是各子平面上的方向角θ须经过角度变换到O4平面。下面将一一
θθθ分别代表子坐标系上的目标方位角θ1,θ2,θ3投影到虚拟平面O4后的值,正方向校准后,雷达2和雷达3的正方向应与雷达1统一,即123, ,说明。
2.3.1 校准正方向 方位角定义为以正北方向为基准,按顺时针旋转所成的角度。若123
',','
θθθ,分别代表平面O上的校准正方向后的目标方位角,则
''''''
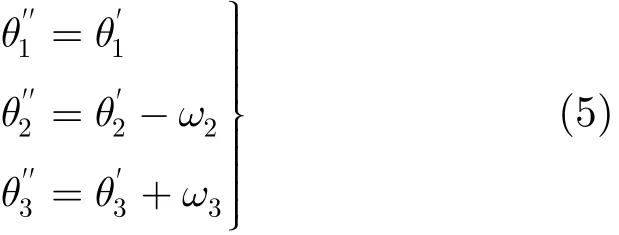
其中
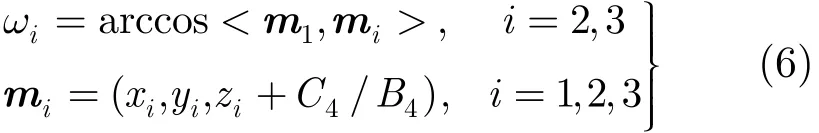
mi为雷达i的正北方向在平面O4上的投影向量。通过式(5),即可消除不同雷达在不同位置所在的正北方向造成的角度偏差。
2.3.2 方位角变换 各子平面上的方位角θ1,θ2,θ3须投影变换到虚拟平面O4上的,,。下面将以雷达1为例,介绍方位角变换的基本方法。如图2所示,O1为雷达1站址,平面O1为雷达1子坐标平面,平面O4为虚拟平面。CO1为两平面交线。在子平面和虚拟平面分别作过O1点且垂直于CO1的法线O1D, O1E。则∠EO1D为两平面的夹角,记为γ。设向量O1B为雷达1子坐标系的正北方向,O1B与法线O1D的夹角∠BO1D记为α。向量O1A为目标T的方向,O1A与法线O1D的夹角∠AO1D记为β。则∠AO1B为雷达1在子坐标系下的目标方位角θ1,即θ1=α+β。分别过A, B点做垂直于平面O1的垂线,交于虚拟平面O4的M, N两点。则∠MON为变换到虚拟平面的目标方位角。
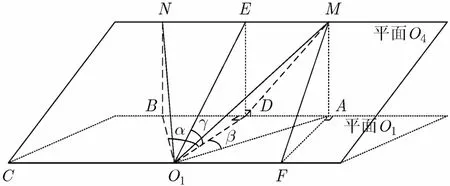
图2 方位角变换示意图
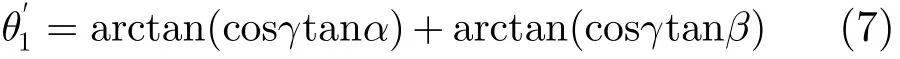
求解α,β,γ的值,即可求解情况推导的过程与之类似。由于篇幅所限,具体推导过程就不再详述。
2.4 坐标系变换
下面探讨地球坐标系上与虚拟平面坐标系O4之间的坐标变换问题。若一点在地球坐标系中的坐标为(x,y,z),那么它在虚拟平面坐标系O4的坐标(x',y',z')可以表示为
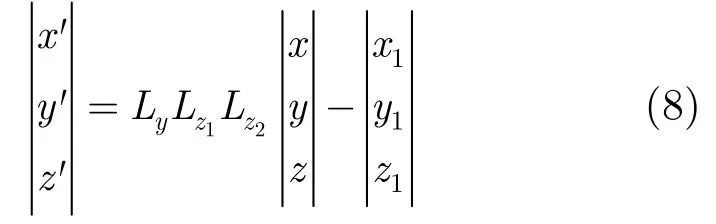
其中

本文须将O2(x2,y2,z2), O3(x3,y3,z3)投影到平面O4上,所以将这两点代入式(8),即可得到两点在新坐标系O4的坐标。与此同时,在虚拟平面搜索得到目标T坐标(xm,yn,zm,n)之后,可通过逆变换,把目标位置转回到地球坐标系。
3 搜索算法
3.1 搜索范围的选取
本文采用分辨率不高,但数据稳定性好的方位角信息确定算法的搜索范围。如图3所示,在O4平面以各雷达站站址为原点,画方位角为(θi+σθi), (θi−σθi)的两条射线,这两条线所夹的区域为目标可能所在的区域。任意两雷达交汇成一个四边形区域。如图所示,雷达2与雷达3所交汇的区域为四边形abcd。这样就可以得到3个四边形作为搜索区域。当两雷达与目标T所成的夹角(如∠O1TO2)趋于0°或180°时,搜索四边形区域会被拉长,导致搜索范围过大,降低搜索速度和搜索精度。所以本文只选取夹角与90°最为接近的两雷达所交汇的搜索区域(图中为abcd)作为最后的搜索范围。
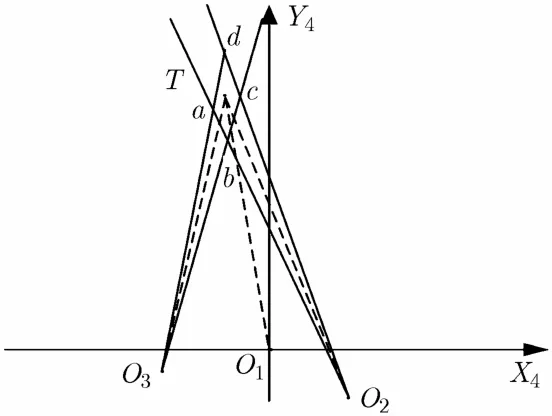
图3 搜索范围的选取示意图
3.2 误差最小值的搜索
根据以上方法可以得出目标位置落在一定区间内,可在这个区间内按照一定的搜索步进对x, y值进行搜索,对每组给定的搜索坐标值均可求出其对应的高度z值。
假定在搜索范围内,x的取值个数为M, y的取值个数为N,则可以得到M×N组高度值zm,n,其中zm,n由式(10)计算获得。
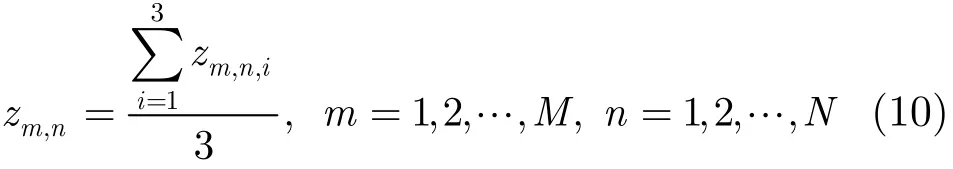
其中,zm,n,i表示由第i个雷达计算得到的高度值。
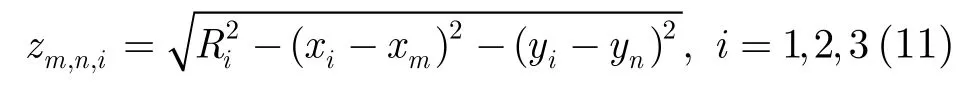
其中, (xi, yi)是雷达站i的O4平面的直角坐标,(xm, yn)是飞行目标的在O4平面的投影坐标。最后,针对米波雷达目标方位信息误差较大,本文仅应用分辨率较高的目标距离信息来获取目标高度估值,对于一个由3个雷达(包括一个或多个米波雷达)组成的组网雷达来说,其联合误差为
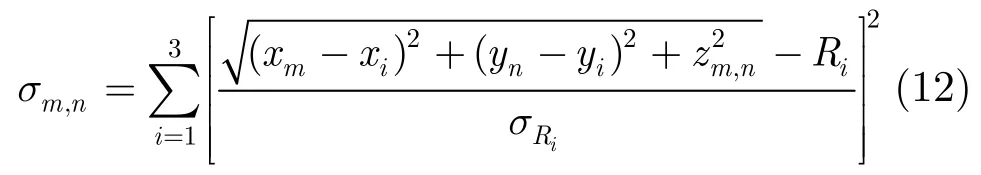
σRi为雷达站i目标距离的均方差。σ由于为3个服从N(0,1)分布的变量的平方和,将服从自由度为3的χ2分布[12,13]。根据式(12)计算误差函数,令σ分别对x, y, z求导,并使其导数为零,求解方程组就可以得到目标的估计位置(x, y, z)[9]。对于极小化误差法,其在运算速度方面有着明显的缺陷,并且方程组易出现无解或死循环的情况,即不能保证各个量的偏导数同时为零,严重影响了极小化误差的适用范围。本文采用σ对应最小值的点(xm,yn,zm,n)作为目标位置的最佳融合估计值,使其具有更好的计算性能和稳定性。
4 置信度判断
由于地面强反射的原因,目标的距离估值有些时候是不准确的,需设立判决准则验证定位的有效性。通过以上改进算法搜索得到目标的最佳估计坐标值(xm,yn,zm,n),可通过逆变换,把目标T位置信息变换回到地球坐标系,得到目标T精确位置(xT,yT,zT),通过该信息可以反推得到各雷达到该点的目标距离。
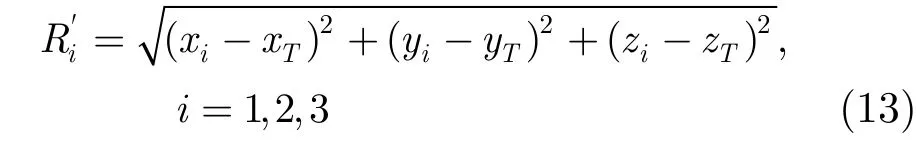
在高斯噪声背景下,雷达测量所得到的目标距离Ri是服从高斯分布的。即
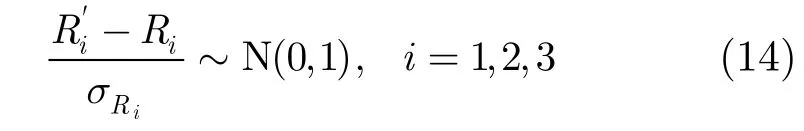
其中σRi是Ri均方差,可以用各雷达的距离分辨率的一半代替。若置信度设置为95%,则
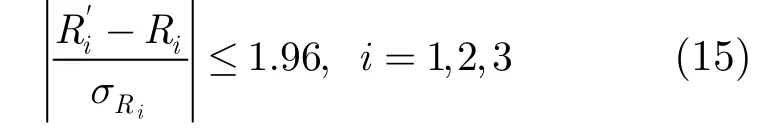
为真,则认为(BT,LT,HT)为最佳估计坐标值,否则予以剔除。
5 算法流程图
图4为算法的流程图。算法首先将3个雷达站址的大地坐标数据转换成统一的地球坐标,在地球坐标系上,利用3雷达的站址坐标建立虚拟平面。通过坐标转换和数据转换,把3雷达站址地球坐标和子坐标量测数据转换到该虚拟平面上。在该平面利用改进的最小误差法对飞行目标定位。得到的虚拟平面上的最佳估计坐标需反变换到地球坐标系,做目标距离量测的置信度检验。当置信度判决成立时,最后将目标精确位置的地球坐标做大地坐标的反变换,输出代表目标唯一方位的纬度、经度和海拔高度值。
6 虚拟平面的优势
无论是在传统的地球表面切面为工作平面的传统坐标系,还是在本文所提出的虚拟平面上,在搜索计算过程中,需要按式(11)计算目标在平面上的高度值zm,n,i。
可以看出,在平面上如果目标的真值位置,Z的值较小,而X和Y方向的误差较大时,会造成式(11)根号内的值小于零,而使zm,n,i无解,致使算法失灵。但由于本文所建立的虚拟平面可以通过雷达布站使得特定位置的目标保持在虚拟平面上适当的高度,从而避免了上述问题发生,提高了算法的稳定性和定位精度,增强了对低空目标的检测概率。这是优于传统坐标系定位方法的地方。这也给雷达布站提供了一个全新的思路。
7 仿真分析
7.1 算法的精度分析
仿真参数:本文仿真了两种雷达布站的方式。第1种为3雷达布站成站间距较小的锐角三角型,雷达站址数据如表1所示。设定目标真实海拔高度Hr=10 km。设3雷达的距离分辨率为0.1 km,方位分辨率为0.5°。所以根据先验知识,仿真时假设距离量测噪声服从(0, 0.052)的高斯分布。方位量测噪声服从(0, 0.252)的高斯分布。每个实验重复作40次,相对误差ΔH= |H−Hr|,所得结果为40次的平均值。
如图5所示,为第1种布站下,目标不同位置所得到的海拔高度相对误差的等高线图。横、纵坐标为目标所在的经、纬度。该图南北约260 km,东西约220 km。“*”代表雷达位置。由图5可知测高精度随目标到雷达阵的距离成反比。各方向所得到的测高精度几乎相同。可以认为该算法的测高精度是相对优秀的。
第2种布站时,在第1种布站的基础上,拉大了站间距离,3雷达成钝角三角形。雷达站址数据如表1所示。其他数据与第1种布站相同。如图6,该等高线图与图5相比,在东西方向的等高线角密集,测高精度有所降低。在南北方向更加平直,同样获得了较好的测高精度。
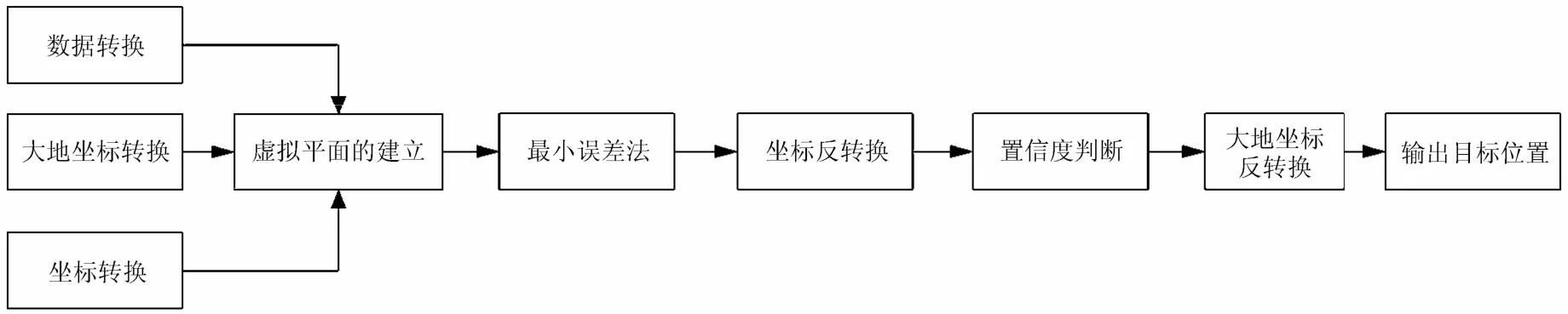
图4 算法的流程图
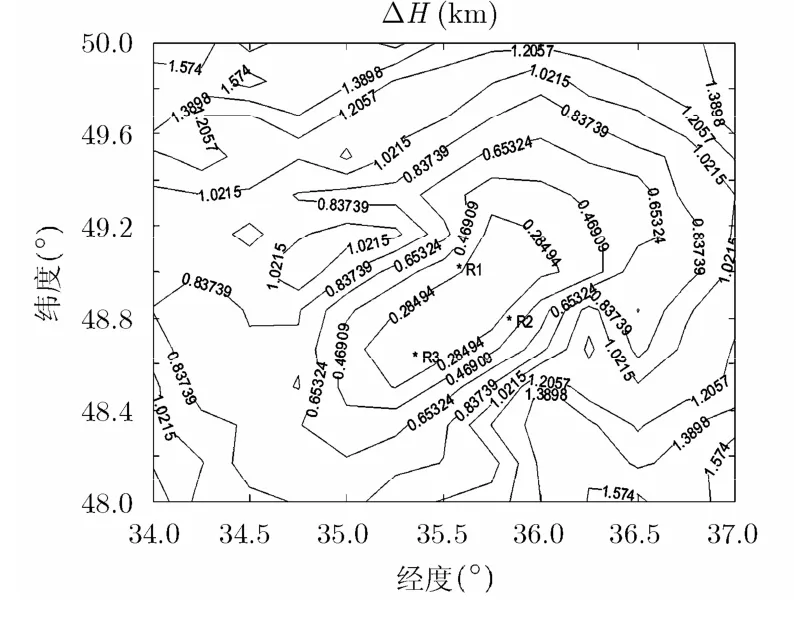
图5 站间距较小的锐角三角型布站下的测高误差等高线图
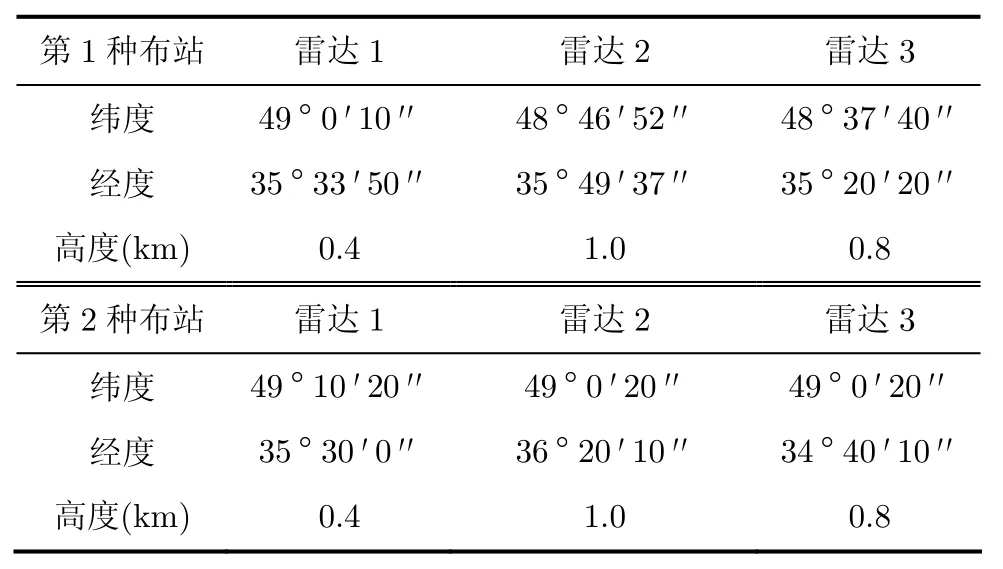
表1 雷达站址数据
7.2 雷达布站对测高精度的影响
指定目标真实位置大地坐标在点(50.0°,35.5°, 10 km)处,距离坐标原点约130 km。在第2种布站的基础上只改变雷达1的站址高度,观察目标相对虚拟平面的高度,以及高度误差随雷达1站址高度的变化。如表2所示,在该点处,随着雷达站址高度的升高,在目标海拔高度不变的情况下,目标相对虚拟平面的高度在降低,测高误差在雷达1海拔高度为0.4 km处最小,并向两侧逐步上升。由此可见,通过雷达布站,寻找特定的虚拟平面可以提高对特定方位的目标的测高精度。这是优于传统坐标系定位方法的地方。也给雷达布站提供了一个全新的思路。
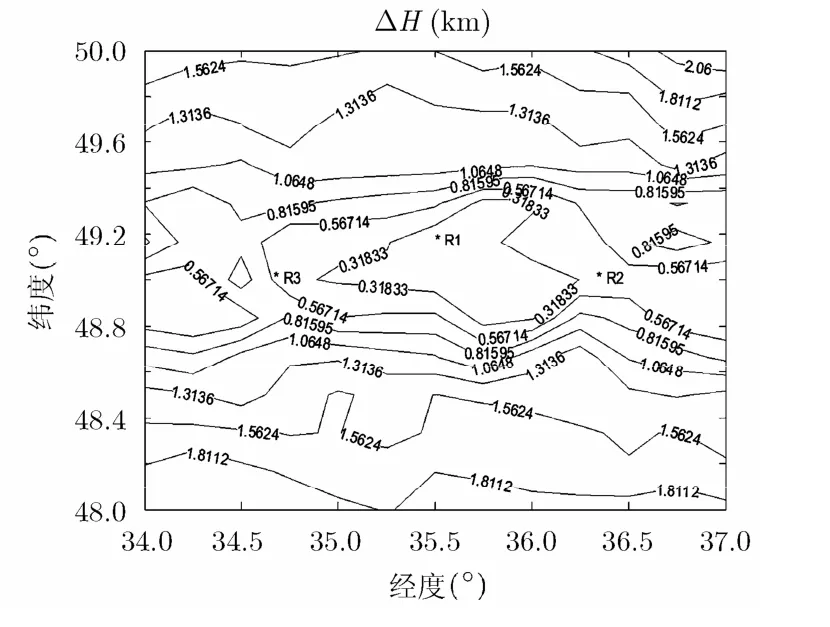
图6 站间距较大的钝角三角型布站下的测高误差等高线图
8 结论
仿真分析得出,本文提出的基于虚拟平面的测高算法克服了当目标距离比较远时,地球曲率对目标高度的影响。并通过雷达布站,寻找特定的虚拟平面可以提高对特定方位的目标的测高精度。仿真分析可以看出,该算法获得了较好的测高精度。该算法可作为组网雷达行之有效的测高方法。此外,本文所建立的虚拟平面的数学模型同样适用于其他信号、数据处理。该工作平台基于大地坐标系,可以有效地实时地表达各自坐标的数据信息,有利于数据间的传输与融合。

表2 雷达布站对测高精度的影响
[1] 李静明, 丁建江. 雷达低仰角下复杂地形反射特性研究[J]. 火控雷达技术, 2013, 42(3): 25-27, 38.
Li Jing-ming and Ding Jian-jiang. Study on complex terrain reflection characteristics at low elevation of radar[J]. Fire Control Radar Technology, 2013, 42(3): 25-27, 38.
[2] 赵英俊, 李荣锋, 王永良, 等. 基于主瓣多径干扰抑制的米波雷达测角方法[J]. 华中科技大学学报(自然科学版), 2013, 41(4): 51-55.
Zhao Ying-jun, Li Rong-feng, Wang Yong-liang, et al.. Angles measurement of meter-wave radars by multipath jamming suppression[J]. Journal of Huazhong University of Science and Technology (Netural Science Edition), 2013, 41(4): 51-55.
[3] Chen Bai-xiao, Zhao Guang-hui, and Zhang Shou-hong. Altitude measurement based on beam split and frequency diversity in VHF radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 3-13.
[4] 朱伟, 郑轶松, 陈伯孝. 约束MUSIC算法在米波雷达低仰角测高中的应用[J]. 安徽大学学报(自然科学版), 2014, 38(4): 59-65.
Zhu Wei, Zheng Yi-song, and Chen Bai-xiao. Application of constrained MUSIC to the low-angle altitude measurement for VHF radar[J]. Journal of Anhui University(Natural Science Edition), 2014, 38(4): 59-65.
[5] 吴向东, 马仑, 梁中华. 基于波束域的米波雷达低仰角波达方向估计[J]. 电波科学学报, DOI: 10.13443/j.cjors. 2013103101.
Wu Xiang-dong, Ma Lun, and Liang Zhong-hua. Estimation of direction-of-arrival for meter-wave radar based on beam-space at low-angle environment[J]. Chinese Journal of Radio Science, DOI: 10.13443/j.cjors. 2013103101.
[6] 杨广玉, 杨雪亚. 基于RELAX的米波雷达测高方法[J]. 科技信息, 2014(1): 75, 101.
Yang Guang-yu and Yang Xue-ya. Height measurement algorithm of meter-wave radar based on RELAX[J]. Science & Technology Information, 2014(1): 75, 101.
[7] 朱伟. 米波数字阵列雷达低仰角测高方法研究[D]. [博士论文],西安电子科技大学, 2013.
Zhu Wei. Study on low-angle altitude measurement in VHF Radar[D]. [Ph.D. dissertation], Xidian University, 2013.
[8] 孙仲康, 周一宇, 何黎星. 单多基地有源无源定位技术[M].北京: 国防工业出版社, 1996: 118-131.
Sun Zhong-kang, Zhou Yi-yu, and He Li-xing. The Technology of Active and Passive Positioning of Monostatic or Multistatic Radars[M]. Beijing: National Defence Industry Press, 1996: 118-131.
[9] 赵振山, 杨万海. 组网雷达定位优化算法[J]. 雷达与对抗, 2002(3): 1-4, 11.
Zhao Zhen-shan and Yang Wan-hai. Optimal locating algorithm in networking radar[J]. Radar & ECM, 2002(3): 1-4, 11.
[10] Bowring B R. Transformation form spatial to geographical coordinates[J]. Survey Review, 1976, 23(181): 323-327.
[11] Bowring B R. The accuracy of geodetic latitude and height equations[J]. Survey Review, 1985, 28(181): 202-206.
[12] Schmidt R O. A new approach to geometry of range difference location[J]. IEEE Transactions on Aerospace and Electronic Systems, 1972, 18(6): 821-835.
[13] 黄喜军, 韩传久, 张彤. 组网雷达距离信息实现目标3维定位[J]. 火力与指挥控制, 2005, 30(S1): 121-122.
Huang Xi-jun, Han Chuan-jiu, and Zhang Tong. Threedimension target location using range information measured by networking radar[J]. Fire Control and Command Control, 2005, 30(S1): 121-122.
夏 添: 男,1985年生,博士生,研究方向为雷达信号处理、信息融合.
沈一鹰: 男,1960年生,教授,主要研究方向为雷达目标检测、海量数据融合.
刘永坦: 男,1936年生,中国科学院院士、中国工程院院士,主要研究方向为雷达目标检测、信号处理.
陈 迪: 男,1979年生,讲师,主要研究方向为雷达数据处理.
Height Measurement Algorithm of Meter-wave Radar Network Based on Virtual Plane
Xia Tian Shen Yi-ying Liu Yong-tan Chen Di
(School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China)
With development of anti-stealth technology, meter-wave radar comes into sight of scientific community again due to its natural superiority of anti-stealth and anti-radiation missile. But as strongly influenced by multipath effect in process of detecting target with low elevation angle, meter-wave radar may obtain a measured height with large deviation that unable to meet actual need. However, the development of data fusion technology in radar network finds a solution to this problem. This paper uses data fusion technology of radar network to realize three-dimensional positioning of target only with distance and azimuth information measured by meter-wave radar, so that the problem of height measurement in meter-wave radar can be well solved. In consideration of effect of earth curvature, the proposed height measurement algorithm of meter-wave radar network utilizes geodetic coordinate transformation, coordinate system transformations, and data transformation to unite all radar's data into one reasonable work platform, namely virtual plane. Height measurement is conducted to target on this plane. Azimuth angle information with not high resolution ratio but good data stability is used to determine hunting zone of algorithm so as to improve minimum error method. The target distance information with high resolution ratio is used to obtain final longitude, latitude and altitude estimate of target. Sometimes target distance estimate may be inaccurate as a result of strong reflection on earth surface, according to which a confidence judgment criterion is established to verify availability of positioning. Through the simulation analysis, the proposed algorithm is verified to obtain a good accuracy in height measurement and can be regarded as an effective method in height measurement for radar network.
Meter-wave radar; Radar network; Height measurement; Virtual plane; Minimum error method
TN959.2+2
: A
:1009-5896(2015)06-1476-07
10.11999/JEIT141504
2014-11-27收到,2015-02-12改回
*通信作者:夏添 xiatianhit@126.com
