平台运动测量误差对阵列天线合成孔径雷达三维成像影响分析
2015-07-12丁振宇谭维贤王彦平洪文吴一戎
丁振宇谭维贤王彦平洪 文吴一戎
①(中国科学院电子学研究所 北京 100190)
②(微波成像技术重点实验室 北京 100190)
③(中国科学院大学 北京 100190)
平台运动测量误差对阵列天线合成孔径雷达三维成像影响分析
丁振宇*①②③谭维贤①②王彦平①②洪 文①②吴一戎①②
①(中国科学院电子学研究所 北京 100190)
②(微波成像技术重点实验室 北京 100190)
③(中国科学院大学 北京 100190)
阵列天线合成孔径雷达(SAR)可实现3维成像。为了提高成像质量,使用测量设备获取平台的运动信息以进行运动补偿,而测量误差会影响补偿及成像质量,需对其进行分析。该文首先建立了阵列天线SAR 3维成像模型和测量误差分析模型,接着分别从位置和姿态角两个方面分析了测量误差对相位误差的影响,并比较不同方向误差影响的大小,然后通过仿真分析了误差对成像指标的影响,并引入姿态误差基线比来量化姿态角误差的影响。最后得出高程向和横滚角测量误差影响最大的结论,给出了限定要求下测量误差的容忍值。该文的结论为测量设备的选取和设计以及成像和补偿方法的选择和分析提供了理论指导和参考。
合成孔径雷达;阵列天线; 3维成像;测量误差;误差分析
1 引言
阵列天线合成孔径雷达(SAR)通过航迹向合成孔径、跨航向等效为线性均匀阵列和波传播方向的宽带信号实现3维分辨[1,2],广泛应用于城市测绘、灾害监测等领域[3]。阵列天线SAR一般工作在波分和时分两种模式。对于前者,一般发射正负线性调频信号以区分波形,缺点是当需要两个以上发射天线时,信号波形设计难度很大[4]。因此,当需要较多发射通道时常采用时分模式。此时,天线在不同脉冲间发生位移,需要补偿该位移后才能等效为一个线性均匀阵列[5−7]。此外,运动误差使得天线的相位中心偏离理想位置,需测量设备获取运动信息以进行补偿,但测量误差会在回波中引入相位误差,对成像造成影响。因此在补偿之前,需分析测量误差对成像的影响。当前的研究工作主要集中在成像算法[5−14],也有涉及误差补偿,但忽略了测量误差的影响[15]。文献[16]在时分模式下,从等效后的线性均匀天线阵列出发,分析了天线相位中心偏差对成像的影响,却忽略了测量误差对于等效前平台运动的影响。因此在进一步研究成像和补偿方法前,对测量误差影响的分析十分必要。本文首先建立了阵列天线SAR的3维成像模型,接着分析了时分工作模式下的等效相位中心误差和平台运动带来的影响,然后建立了测量误差分析模型,并从位置和姿态角误差两个方面分析了测量误差对回波中的相位误差的影响,比较不同方向误差的影响大小,接着通过仿真分析了测量误差对成像指标的影响,验证了理论分析的正确性。该文为阵列天线SAR系统中测量设备的指标分配和参数设计提供理论依据,为成像及补偿方案的分析和选择提供了参考。
2 阵列天线SAR下视3维成像原理
2.1 成像几何
如图1所示,运动平台沿航迹向x轴以速度V作匀速直线运动,阵列天线沿跨航向y轴分布,阵列中心位于原点,向下建立z轴代表高程方向,x,y,z轴满足右手螺旋准则。成像区域位于平台下方,点目标P的坐标为(x0,y0,z0),散射系数为σ。阵列天线包括2M个发射天线Txm和N个接收天线Rxn,跨航向坐标分别为yTm和yRn,其等效相位中心TRmn的跨航向坐标为ymn=(yTm+yRn)/2。
2.2 等效相位中心误差及平台运动的影响
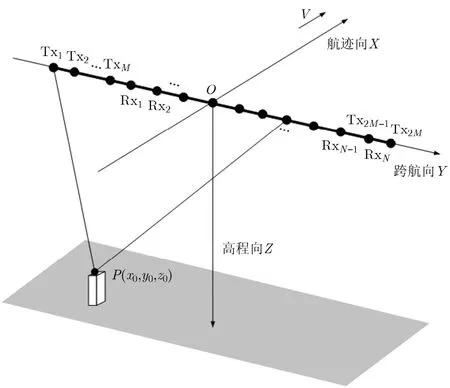
图1 阵列天线SAR 3维成像几何模型
时分模式下,发射天线顺序发射脉冲,重复频率为Fa,所有接收天线同时接收回波。在航迹向第l个采样位置和第m个脉冲时刻,收发天线到点目标P的距离历程Rreal及等效相位中心的距离历程RTRmn分别为
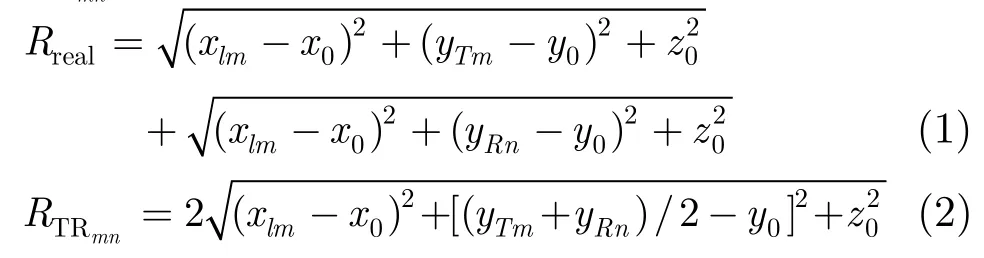
其中,xlm=2MV(l−L)/Fa+V(m−1)Fa, l∈[1,2L−1]代表航迹向采样点序号;m∈[1,2M]代表发射天线序号。Rreal和RTRmn之差即等效相位中心误差ΔRTRmn,如式(3)所示,其中。V(m−1) /Fa代表m个脉冲期间平台沿航迹向的位移量,它使等效相位中心不再位于一条直线,无法等效为线性阵列[1],需进行补偿,补偿后等效相位中心的坐标为(xl1,(yTm+yRn)/2,0),到点目标P的距离RTRLmn如式(4)所示。其中xl1=2MV(l−L)/Fa。
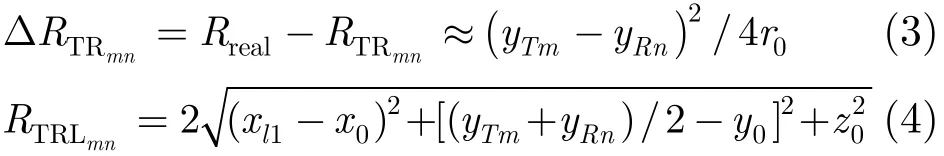
平台位移带来的距离误差ΔRTRL和相位误差ΔψTRL如式(5)和式(6)所示。其中fc代表信号的载波频率,f代表基带频率,c代表光速。
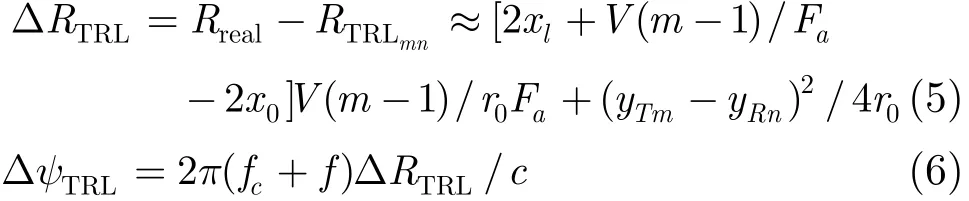
实际补偿时,由于点目标的真实坐标(x0,y0,z0)未知,一般采用场景中心点Pce(xce,yce,zce)作为参考目标进行补偿,补偿相位如式(7)所示。其中rce=。补偿后,参考点回波的误差被准确补偿,其他点目标回波中还存在残留相位误差Δψres= ΔψTRL−ΔψTRLce。对于这一误差,可对场景进行分块补偿。

3 测量误差影响分析
3.1 测量误差分析模型
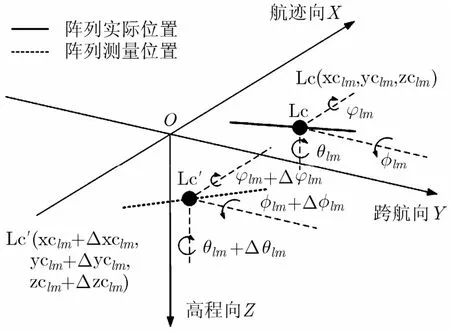
图2 测量误差示意图
如图2所示,测量设备位于阵列中心,测量其位置坐标和姿态角,(ϕ,φ,θ)分别对应横滚角、俯仰角和偏航角。阵列中心的真实位置和姿态角如实线所示,测量所得如点线所示,测量误差为(Δxlm, Δylm,Δzlm)和(Δϕlm,Δφlm,Δθlm)。对于刚性阵列,天线单元之间相对位置固定,可根据阵列中心的位置和姿态角得到所有单元的位置坐标。则根据测量值换算得到的收发天线的位置坐标如式(8)和式(9)所示。其中
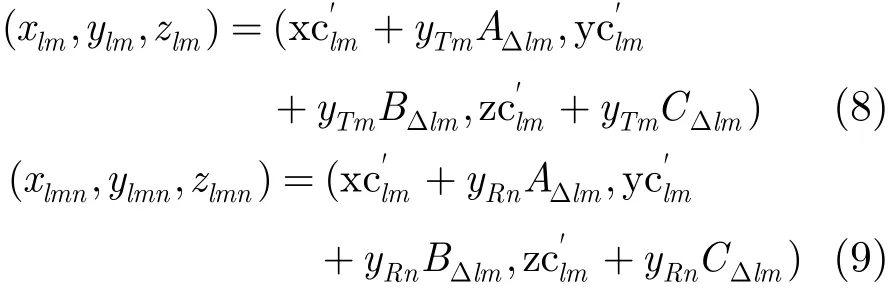
另一方面,收发天线的真实坐标分别为

其中,Alm=cosφlmsin θlm,Blm=sinϕlmsinφlmsin θlm+cosϕlmcos θlm,Clm=cosϕlmsinφlmsinθlm−sin ϕlm⋅cosθlm。补偿阵列单元不同脉冲间的平台位移后,等效相位中心坐标的真实值和测量值分别为

设收发天线的真实位置到点目标P的距离历程(简称真实距离)为Rre,根据测量值换算得到的收发天线位置到参考点目标Pce的距离历程(简称测量距离)为Rme。补偿平台位移后,等效相位中心的真实位置到P的距离历程(简称真实等效距离)为Rre-eq,根据测量值换算得到的等效相位中心的位置到Pce的距离历程(简称测量等效距离)为Rme-eq。如2.2节所述,按测量值和参考点补偿后的残留相位误差Δψres如式(14)所示。

Δψres中与测量误差有关的项即测量误差带来的相位误差。实际工作中,平台运动非理想,速度变化导致航迹向非均匀采样,xcl1不再均匀分布;平台震颤导致阵列中心晃动,即yclm和zclm发生变化。这使Δψres更为复杂。本文分析测量误差的影响,因此在以下分析中忽略运动误差,令(ϕ,φ,θ)=0, yclm=zclm=0,xclm=2MV(l−L)/Fa+V(m−1) /Fa。
3.2 位置测量误差的影响
此时,只考虑位置测量误差(Δxlm,Δylm,Δzlm)的影响,令(Δϕlm,Δφlm,Δθlm)=0。根据式(14),忽略误差高次项后,相位误差Δψres可表示为
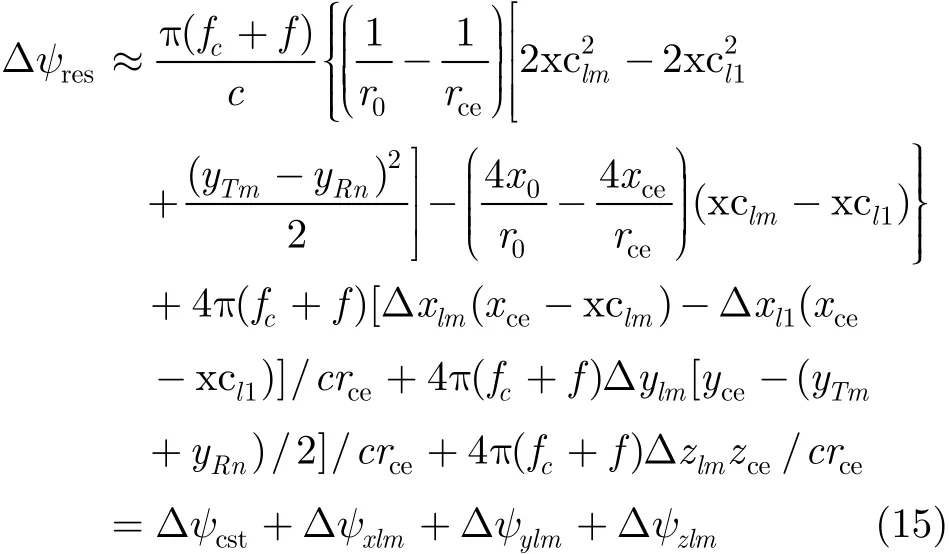
Δψres包括测量误差无关量Δψcst,航迹向误差分量Δψxlm,跨航向误差分量Δψylm和高程向误差分量Δψzlm。Δψcst由参考点和实际点目标不一致导致,与测量误差无关,假设已得到准确补偿。下面比较不同方向的测量误差对相位误差的影响大小,由于误差的随机性,就是在Δxlm,Δylm,Δzlm独立同分布的情况下,比较相位误差均方根和
~的大小,如式(16)式(18)所示。其中Aprms代表测量误差的均方根。

一般情况下,天线在跨航向和航迹向的波束角较小(小于90°),则因此,最大,即高程向测量误差对相位误差影响最大。
3.3 姿态角测量误差的影响
此时,只考虑姿态角测量误差(Δϕlm,Δφlm, Δθlm)的影响,令(Δxlm,Δylm,Δzlm)=0。根据式(14),忽略姿态角误差的正弦项的高次项,余弦项近似为1后,相位误差Δψres可表示为
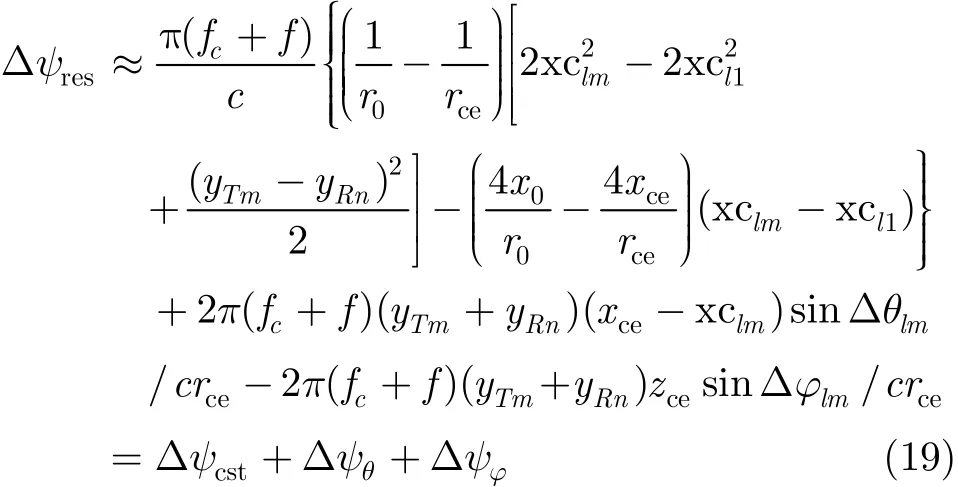
如式(19)所示,Δψres包括测量误差无关量Δψcst,偏航角误差分量Δψθ和横滚角误差分量Δψϕ。由于没有Δφlm相关项,可忽略俯仰角测量误差的影响。类似地,在Δθlm,Δϕlm独立同分布的情况下,比较和的大小,如式(20)和式(21)所示。其中代表测量误差正弦值的均方根。
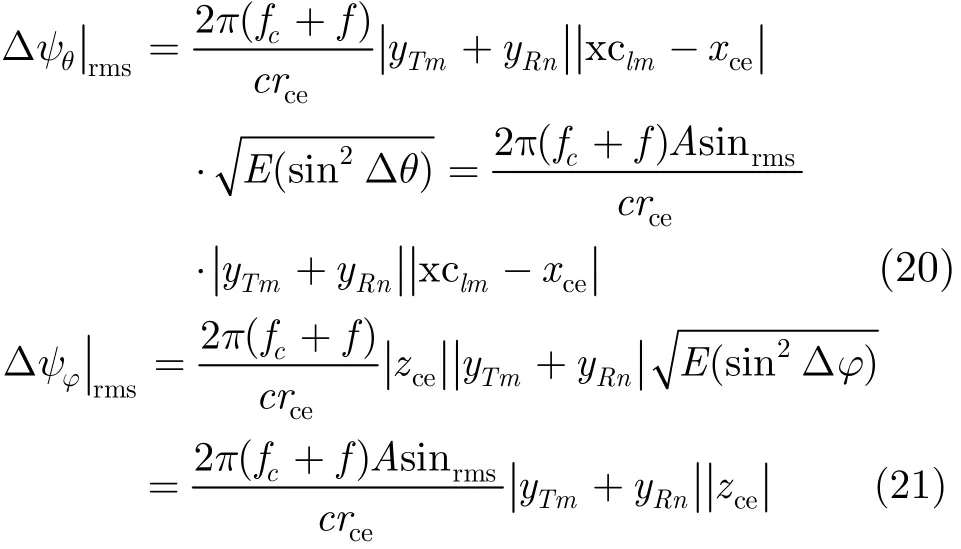
一般情况下,天线的航迹向波束角小于90°,即。因此,|Δψϕ|rms大于|Δψθ|rms;即横滚角测量误差对相位误差影响最大,偏航角次之,俯仰角影响可以忽略。
4 仿真分析
下面仿真分析测量误差对相位误差和成像指标的影响。由于距离和相位一一对应,对相位误差的分析可以转化为对距离误差的分析。此外,姿态角测量误差影响与阵列长度有关:阵列越长,阵列两端的等效相位中心离阵列中心越远,同一姿态角误差下对应的相位误差越大。因此,将姿态角测量误差与阵列长度的比值(简称姿态误差基线比)作为姿态角测量误差的替代。实际工作中设备的测量误差随机分布,仿真中设位置和姿态角测量误差服从N(0,σ2)正态分布。仿真参数如表1所示,点目标位于(0,0,490)。在某一均方根幅度为σ的测量误差下,距离误差随航迹向和跨航向随机变化,取其均方根作为幅度。成像指标包括峰值旁瓣比(PSLR)、积分旁瓣比(ISLR)和分辨率(IRW)。为了消除单次生成误差序列造成的随机性,在同一均方根下多次(50次)计算,取平均值作为结果。测量误差对距离误差的影响如图3和图4所示,对成像指标的影响如图5和图6所示。
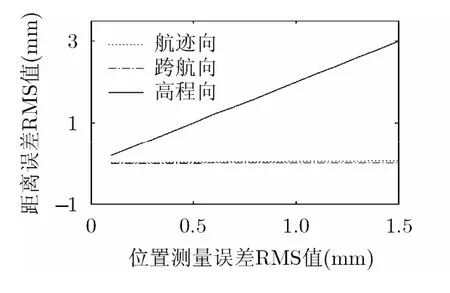
图3 位置测量误差对距离误差影响

图4 姿态角测量误差对距离误差影响
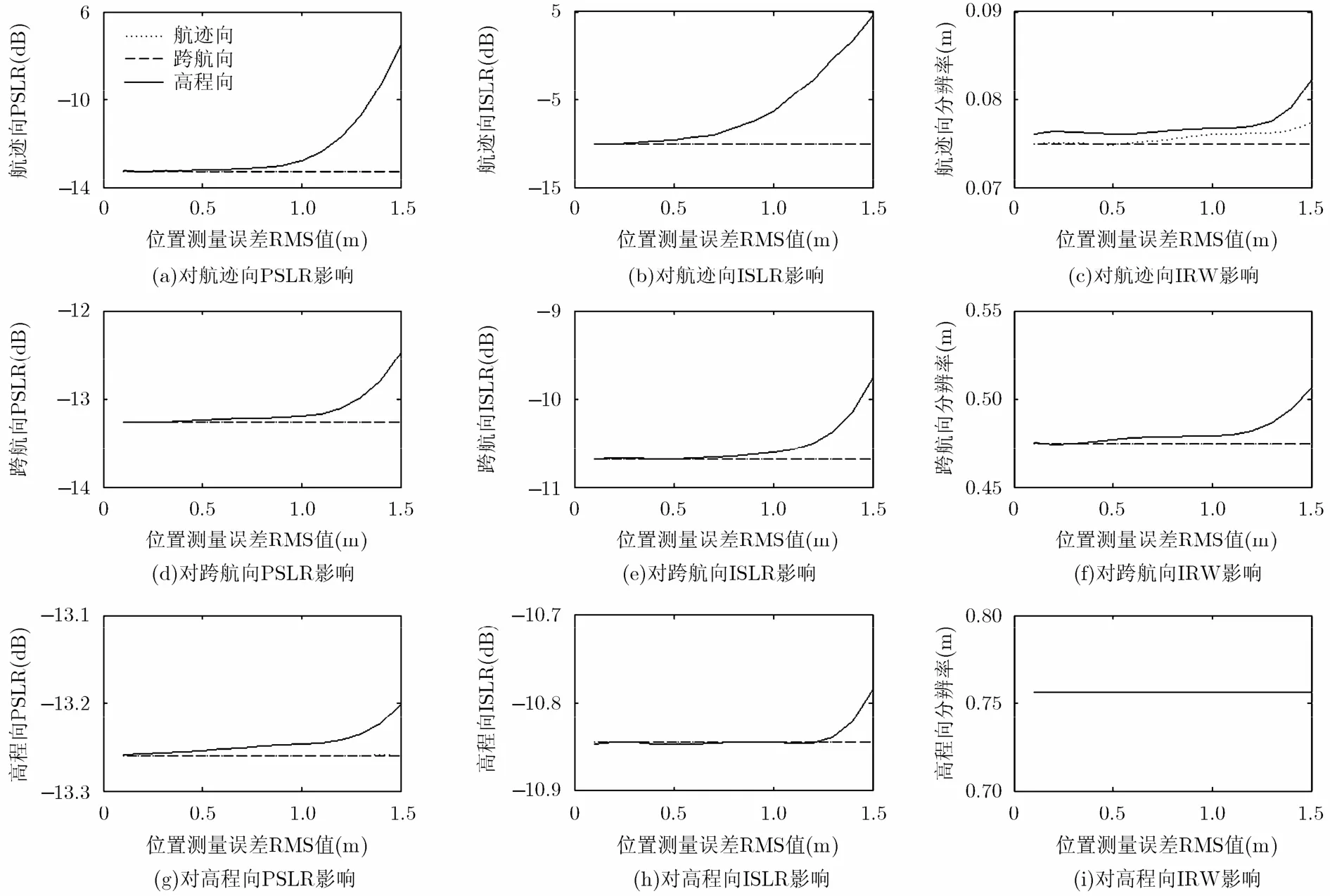
图5 位置测量误差对成像指标的影响

图6 姿态角测量误差对成像指标的影响

表1 仿真参数
由图3可见,高程向测量误差引起的距离误差最大;由图4可见,横滚角测量误差引起的距离历程误差最大,偏航角次之,俯仰角影响最小。由图5可见,高程向测量误差对成像指标影响最大;在相同误差幅度下,航迹向成像指标受影响最大,高程向成像指标受影响最小;不同成像指标间,积分旁瓣比受影响最大。如果允许的最大积分旁瓣比为-7 dB,那么位置测量误差的容忍值为1 mm,即1/8波长。由图6可见,横滚角测量误差对成像指标影响最大,偏航角次之,俯仰角最小;在相同误差幅度下,跨航向成像指标受影响最大,高程向成像指标受影响最小;不同成像指标间,分辨率受影响最大。如果允许的分辨率最大展宽量为25%,那么姿态角测量误差的容忍值为0.03°,对应的姿态误差基线比为0.0073°/m。
5 结束语
时分模式下,天线单元在不同脉冲间发生位移,需要补偿相应的相位误差才能等效为线性均匀阵列。测量误差使得补偿后的回波中仍存在复杂的残留相位误差,从而影响成像质量。在位置测量误差中,高程向误差影响最大,航迹向成像指标和积分旁瓣比最易受影响;在姿态角测量误差中,横滚角误差影响最大,偏航角次之,俯仰角影响最小,跨航向成像指标和分辨率最易受影响。在测量误差符合N(0,σ2)正态分布,信号带宽为200 MHz的情况下,当允许的最大积分旁瓣比为-7 dB时,需要把位置测量误差控制在1/8波长内;当允许的分辨率最大展宽量为25%时,需要把姿态误差基线比控制在0.0073°/m内。本文的分析和结论可为测量设备的选取和研制以及后续的补偿处理提供参考和理论依据。
[1] Gierull C H. On a concept for an airborne downward-looking imaging radar[J]. International Journal of Electronics and Communications, 1999, 53(6): 295-304.
[2] Reigber A and Moreira A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142-2152.
[3] 保铮, 刑孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 200-206.
Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technique[M]. Beijing: Publishing House of Electronics Industry, 2005: 200-206.
[4] 杜磊. 阵列天线下视合成孔径雷达三维成像模型、方法与实验研究[D]. [博士论文]. 北京: 中国科学院电子学研究所, 2010.
Du Lei. Study on model, algorithm and experiment for downward-looking synthetic aperture radar threedimensional imaging based on linear array antennas[D]. [Ph.D. dissertation], Beijing: Institute of Electronics, Chinese Academy of Sciences, 2010.
[5] Hou Ying-ni, Li Dao-jing, and Hong Wen. The thinned array time division multiple phase center aperture synthesis and application[C]. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium 2008 (IGARSS 2008), Boston, USA, 2008: 25-28.
[6] 彭学明, 王彦平, 谭维贤, 等. 基于跨航向稀疏阵列的机载下视MIMO 3D-SAR 3维成像算法[J]. 电子与信息学报, 2012, 34(4): 943-949.
Peng Xue-ming, Wang Yan-ping, Tan Wei-xian, et al.. Airborne downward-looking MIMO 3D-SAR imaging algorithm based on cross-track thinned array[J]. Journal of Electronics & Information Technology, 2012, 34(4): 943-949.
[7] 侯颖妮. 基于稀疏阵列天线的雷达成像技术研究[D]. [博士论文], 北京: 中国科学院电子学研究所, 2010.
Hou Ying-ni. Study of radar imaging technology based on sparse array antenna[D]. [Ph.D. dissertation], Beijing: Institute of Electronics, Chinese Academy of Sciences, 2010.
[8] Nouvel J F, Ruault du Plessis O, Svedin J, et al.. Along track interferometry on rhone river[C]. Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2008: 495-497.
[9] Peng Xue-ming, Wang Yan-ping, Tan Wei-xian, et al.. Downward looking 3D SAR based on uniform virtual phase centre restricted symmetrical distributed thinned array[C]. Proceedings of the 2011 IEEE CIE International Conference on Radar, Xi'an, China, 2011(l): 380-383.
[10] 于春艳, 谢亚楠, 赵海兰, 等. 基于新型阵列配置的机载MIMO-SAR下视三维成像性能研究[J]. 电子测量技术, 2014,37(2): 64-69.
Yu Chun-yan, Xie Ya-nan, Zhao Hai-lan, et al.. Airborne downward-looking MIMO 3D-SAR imaging properties based on the new array configuration[J]. Electronic Measurement Technology, 2014, 37(2): 64-69.
[11] Wang Jie, Liang Xing-dong, Ding Chi-biao, et al.. An improved OFDM chirp waveform used for MIMO SAR system[J]. SCIENCE CHINA Information Sciences, 2014, 57(6): 65-73.
[12] 张清娟, 李道京, 李烈辰. 连续场景的稀疏阵列SAR侧视三维成像研究[J]. 电子与信息学报, 2013, 35(5): 1097-1102.
Zhang Qing-juan, Li Dao-jing, and Li Lie-chen. Research on continuous scene side-looking 3D imaging based on sparse array[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1097-1102.
[13] 彭文杰. 基于压缩感知的阵列SAR三维成像方法研究[D]. [硕士论文], 成都: 电子科技大学, 2013.
Peng Wen-jie. Array SAR 3D imaging method based on compressed sensing[D]. [Master dissertation], Chengdu: University of Electronic Science and Technology of China, 2013.
[14] 韦顺军. 线阵三维合成孔径雷达稀疏成像技术研究[D]. [博士论文], 成都: 电子科技大学, 2013.
Wei Shun-jun. Research on linear array three-dimensional synthetic aperture radar sparse imaging technology[D]. [Ph.D. dissertation], Chengdu: University of Electronic Science and Technology of China, 2013.
[15] 杨泽民, 孙光才, 邢孟道, 等. 基于多通道联合自聚焦技术的机载三维SAR运动补偿[J]. 电子与信息学报, 2012, 34(7): 1581-1588.
Yang Ze-min, Sun Guang-cai, Xing Meng-dao, et al.. Motion compensation for airborne 3-D SAR based on joint multi-channel auto-focusing technology[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1581-1588.
[16] 朱海洋, 洪峻, 明峰. 相位中心偏差对机载阵列天线下视3D-SAR成像影响分析[J]. 电子与信息学报, 2012, 34(4): 910-916.
Zhu Hai-yang, Hong Jun, and Ming Feng. Analysis of impact of phase center variations in linear array antenna downwardlooking 3D-SAR imaging[J]. Journal of Electronics & Information Technology, 2012, 34(4): 910-916.
丁振宇: 男,1987年生,硕博连读生,研究方向为合成孔径雷达三维成像理论、成像算法、补偿处理.
谭维贤: 男,1981年生,博士,副研究员,研究方向为雷达系统、轨道(地基)SAR、阵列天线SAR等.
王彦平: 男,1976年生,博士,研究员,研究方向为三维成像SAR、轨道(地基)SAR、阵列天线SAR等.
Impact Analysis of Motion Measurement Error on Array Antenna SAR Three Dimensional Imaging
Ding Zhen-yu①②③Tan Wei-xian①②Wang Yan-ping①②Hong Wen①②Wu Yi-rong①②
①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
②(Key Laboratory of Science and Technology on Microwave Imaging, Beijing 100190, China)
③(University of Chinese Academy of Sciences, Beijing 100190, China)
The array antenna SAR is able to realize the three dimensional imaging. In order to improve the imaging quality, the measurement equipment is adopted to acquire the motion information of the array antenna's platform for the motion compensation. However, the measurement error may impact the quality of compensation and imaging. Therefore analysis of the impact is indispensable. This paper establishes the imaging model and the measurement error analysis model, analyses the impact on phase error from the aspect of position and angle measurement error respectively, compares the impact of measurement error in the different directions, analyses the impact on imaging index by the simulation, and introduces the idea of angle-error-array-length-ratio to quantify the impact of angle error. The conclusion that the measurement error in the height and roll angle has the biggest impact is proposed and the error tolerance in certain conditions is given at last, which provides the theoretical guidance and reference for the choice and design of the measurement equipment and the motion compensation method.
SAR; Array antenna; Three dimensional imaging; Measurement error; Error analysis
TN958
: A
:1009-5896(2015)06-1424-07
10.11999/JEIT141106
2014-08-21收到,2015-01-27改回
国家自然科学基金(61372186)资助课题
*通信作者:丁振宇 dingzhenyusky@sina.cn
