一种基于极坐标格式算法的高分辨SAR成像自聚焦算法

曾乐天梁 毅 邢孟道

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

一种基于极坐标格式算法的高分辨SAR成像自聚焦算法

曾乐天*梁 毅 邢孟道

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对机载聚束合成孔径雷达(SAR)惯导精度无法满足高分辨SAR成像的问题，该文提出了一种结合极坐标格式算法(PFA)的自聚焦算法，即“由粗到精”的混合多阶段参数化最小熵(Hybrid Multistage Parameterized Minimum Entropy, HMPME)距离单元徙动校正方法和基于图像对比度增强(Contrast Enhancement, CE)的变步长迭代相位误差校正方法。该自聚焦算法可以直接嵌入到PFA处理中，精确地补偿了惯导测量精度不足引起的越距离单元徙动(Range Cell Migration, RCM)和相位误差，且对于低对比度、低信噪比场景数据有良好的聚焦性能。最后，利用仿真实验和实测机载聚束SAR数据验证了所提算法的有效性。

合成孔径雷达；极坐标格式算法；自聚焦；参数化最小熵；对比度增强

1 引言

在SAR数据录取过程中，平台会受到大气湍流以及自身抖动等因素的影响，不可能严格地做匀速直线运动。运动误差[1,2]会使SAR回波信号中同时出现包络误差和相位误差，严重影响SAR信号的聚焦，必须对SAR回波数据进行运动补偿处理[3]。现有的运动补偿方法包括基于惯导的运动补偿和基于数据的运动补偿[4,5]。基于惯导的运动补偿往往精度较低，一般只到亚米级，无法满足高分辨SAR成像的误差精度要求，这时，可以采用数据自适应的方法，从数据本身出发，估计出对成像结果有影响的非空变运动误差，并对其进行补偿，以避免出现图像散焦、分辨率损失、脉冲响应函数的旁瓣异常等现象。

现有的自聚焦方法大体可以分为3类：基于图像偏移的方法、基于逆滤波的方法和基于代价函数的方法。基于图像偏移(Map Drift, MD)的多普勒调频率估计运动补偿方法利用估计得到的多普勒调频率反演计算运动误差对应的二次形式，实现运动误差补偿，该方法易于实现，但在估计高分辨SAR成像形式复杂的运动误差时，估计精度达不到要求。相位梯度自聚焦[6,7](Phase Gradient Autofocus, PGA)是SAR运动补偿过程中最常用的一种非参数化逆滤波自聚焦方法，对于含有孤立散射中心的数据，可以精确估计出任意形式的运动误差，但对于信噪比较低、场景中无明显强散射点如沙漠、海面等情况，其误差估计性能较差。QPGA(Quality PGA)[1]则是对传统PGA算法样本选择过程进行优化处理，可以增加几倍的高信杂比样本数量，大大提升了相位梯度估计的精度和效率。基于代价函数的方法[8,9]通过建立相位误差和图像某一代价函数之间的函数关系，通过优化类算法确定使该代价函数达到极值时的相位误差估计值，如基于最小熵的非参数化自聚焦算法[8]，这类算法计算量一般比较大，且容易受迭代算法本身特性的影响。

本文针对高分辨聚束SAR成像过程中惯导精度达不到运动补偿精度要求这一问题，提出了一种高精度的自聚焦方法，对包络误差和相位误差均进行校正，以得到聚焦良好的SAR图像。首先，通过MD算法对低分辨率相位历史数据进行处理，获得相位误差粗略估计值，反解出包络误差并补偿，然后建立参数化的信号包络误差形式和最小熵的函数关系，运用优化算法迭代求解熵值最小时的包络误差估计值，该方法既具有很高的稳健性，又能大大提高算法的收敛速率。针对相位补偿，采用不断调整相位误差以增强对比度的算法，设计了一种基于迭代的变步长多维搜索的“由粗到精”的优化策略，大大提高了相位误差的估计精度。同时，该方法对误差的类型和阶数没有限制，并且对没有明显孤立散射点、低信噪比、低对比度场景的SAR图像，该方法可以获得很好的聚焦效果。该算法还可以利用FFT/IFFT快速实现，提高了算法的实时应用潜力。最后，仿真实验和实测数据处理结果验证了本文算法的有效性和实用性。

2 运动误差模型

聚束SAR成像是指SAR平台在飞行过程中，通过实时调整天线指向，使天线始终指向同一区域，以提高方位向分辨率的成像模式。图1所示为聚束SAR几何模型， SAR平台的理想航迹是位于高度H处的一条直线，而在实际中，由于受到各种因素影响，SAR平台不可能做匀速直线运动，而是沿着一条曲线运动。为方便讨论，这里我们只讨论“一步一停”假设、正侧视模式下斜平面成像的情况。以场景中心点O为坐标原点建立平面直角坐标系，沿航迹方向为X轴的正方向，场景中心到合成孔径中心的方向为Y轴正方向，场景中任意点目标P的坐标为(x,y)，平台在方位慢时间tm时刻的理想位置N和实际位置A的坐标分别为(vtm,Rb)和(vtm+Δx, Rb+Δy)。因此，在tm时刻SAR平台到P和O的理想瞬时斜距分别为

图1 聚束SAR几何模型

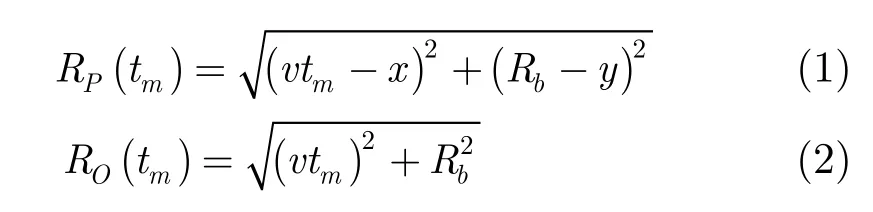
平台到P点的实际瞬时斜距为

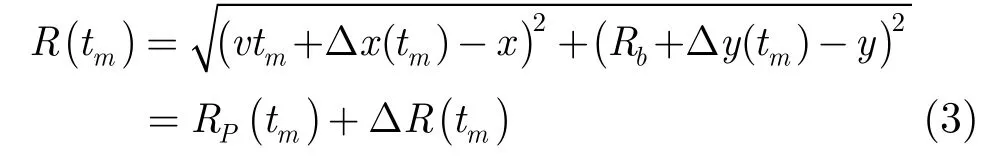
其中ΔR(tm)表示平台非理想轨迹引入的运动误差。

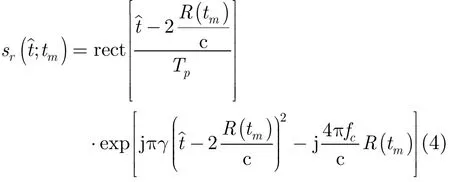
根据PFA算法流程，首先对回波信号进行距离向FFT，然后做距离向匹配滤波、方位Dechirp，再经距离向插值和方位向插值，可得

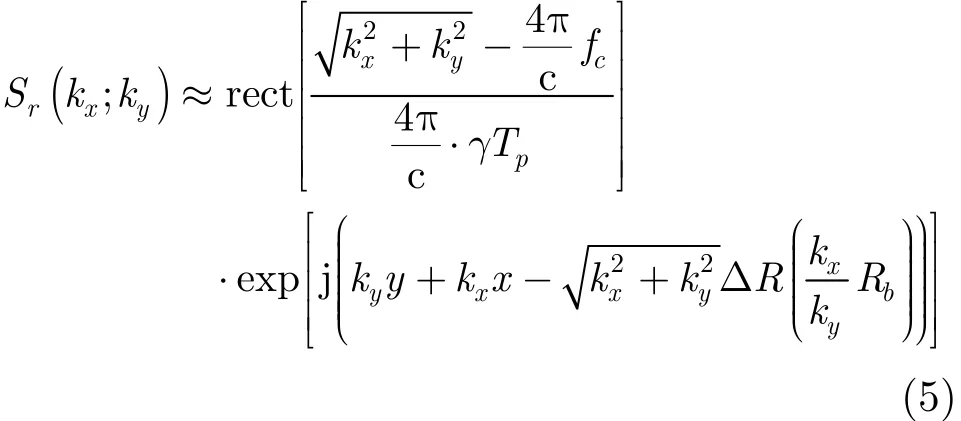
由于受到大气湍流及自身抖动因素影响，平台不可能做匀速直线运动。在进行运动补偿时，我们一般会根据惯性导航系统的信息，对运动误差进行初步的补偿，而对于中等精度的惯性导航系统，系统本身存在测量误差，这种补偿是不彻底的，只能补偿掉部分运动误差，那么剩余的运动误差，即残余运动误差可能引起信号包络的RCM现象和严重的相位误差，使高分辨SAR图像散焦。由于PFA在做方位Dechirp时，忽略了距离差的二次项以及二次以上的残余相位项，这种近似会引起远离场景中心处的图像失真和散焦，而且PFA插值本身会改变包络误差的形式[10]，使包络误差的形式更复杂、难以精确计算，若得不到有效补偿，可能使信号包络的RCM超过一个距离单元，影响SAR图像的方位向处理，降低成像质量。这种影响在高分辨成像场合尤其严重，因此必须将包络误差校正到一个距离单元内，然后才能进行方位向处理。考虑到包络误差和相位误差无法精确计算出来，我们首先将总的包络偏移量看成一个整体，根据由粗到精的思想，对包络误差进行补偿，然后采用对比度增强算法对总的相位误差进行校正，只要将其补偿到一定的误差精度范围内，即包络变化不超过1/4个距离单元，相位变化不超过π/4，就可以得到聚焦良好的图像。

3 基于混合多阶参数化最小熵RCM校正和基于变步长多维搜索的对比度增强相位校正方法

3.1 基于混合多阶参数化最小熵RCM校正方法

一般来说，熵值[11]越小的图像，其聚焦效果越好。本文提出一种“由粗到精”的混合多阶段参数化最小熵算法。首先，对采集的回波数据进行距离脉冲压缩、方位Dechirp, PFA 2维插值、距离IFFT，并对获得的SAR相位历史数据作降采样处理，得到粗分辨的相位历史数据。在该相位历史数据中，信号的包络完全位于同一个距离单元内，此时用MD算法估计出相位误差的粗略值，反解出相应的RCM作为信号包络误差的初始值，然后对PFA插值之前数据的RCM进行补偿。这样，经PFA插值和距离IFFT操作，包络误差的变化范围会大大减小，即RCM会减小。由于PFA算法方位Dechirp时的近似会引入误差，PFA插值操作会改变运动误差的形式，使包络误差、相位误差的形式发生变化，无法精确计算该误差的变化趋势。在上述过程中，我们将所有的包络误差之和看成一个未知量，统一进行补偿，避免计算插值对运动误差的近似影响。

对于高分辨SAR成像场合，经过上述处理，RCM的残余量并不完全处于一个距离单元内，这就需要对RCM进行进一步地精确估计并补偿。通过建立信号包络误差的参数化表达式和图像熵值之间的函数关系，设计多阶段的迭代流程，采用优化算法求解当图像熵值最小时的包络误差估计值，将该估计值作为此时的包络误差，并在数据中进行补偿。

考虑到为获得高方位分辨率的SAR图像，在方位向上积累时间较长，方位向点数较多，通过建立包络误差和图像熵值的函数关系，采用优化算法迭代求解当图像熵值最小时的包络误差估计值，就变成了求解一个以包络误差为自变量的大规模优化问题，求解十分困难。而载机在运动过程中受到惯性的影响，其运动轨迹是连续变化的，包络误差也是连续变化的，我们可以将包络误差Δr的变化看作是随时间连续变化的函数，即，其中P表示多项式阶数，ai表示运动误差多项式的系数，t=[−N/2:N/2−1]/PRF表示方位慢时间，N为方位向采样点数，PRF表示脉冲重复频率。

假设PFA 2维插值之后信号的离散化形式可以表示为x0(m,n)，其中m=0,1,…,M−1, n=0,1,…,N−1,M表示信号在距离向采样点数。由于包络误差的补偿精度在一个距离单元的数量级上且不考虑RCM的空变性，我们可以得到相位历史域数据x(k,n)：其中k=0,1,…,M−1,n=0,1,…,N −1, c0=。经过方位向IFFT，得到聚焦数据g(k,h)的表达式：

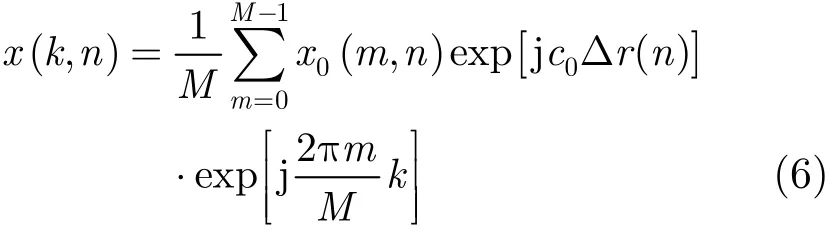
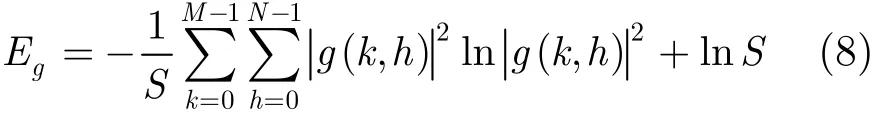
上述问题就简化成为如式(9)所示的优化问题：

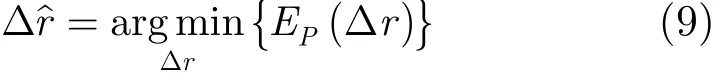
根据共轭梯度算法(Conjugate Gradient Algorithm, CGA)，图像g(k,h)的熵值Eg对包络误差多项式系数ai(i=0,1,…,P −1)的导数可表示为

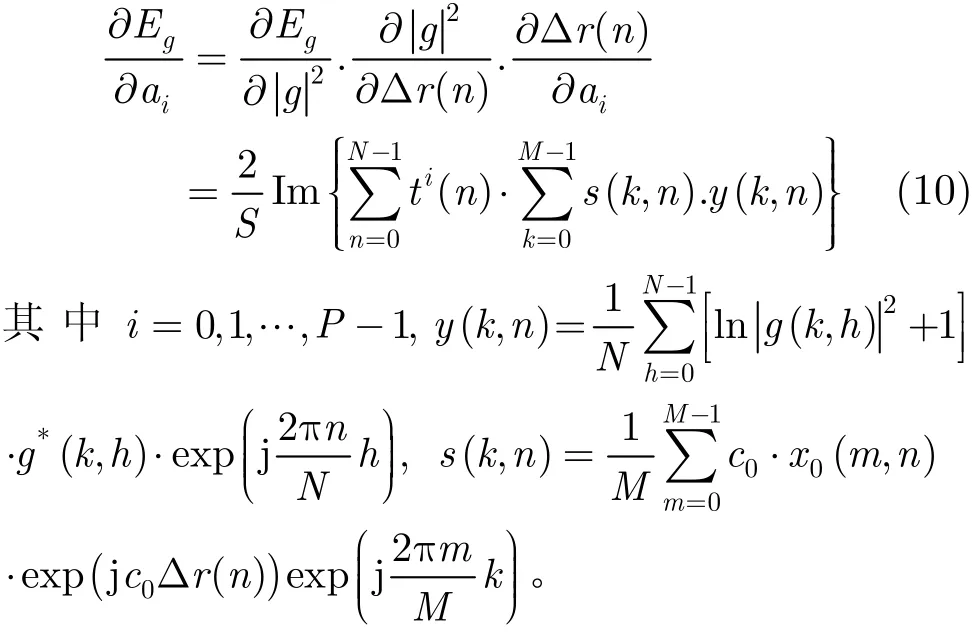
解决此问题需设计多阶段的优化过程迭代求解图像熵值函数的最小值，减小局部极小值的影响。然而，在SAR信号处理中，对信号包络误差(RCM)和相位误差的补偿精度并不相同，包络的补偿精度为1/4个距离单元，而相位的补偿精度必须小于π/4。经过包络补偿之后，剩余的运动误差虽然不会造成RCM，但是残余的相位误差仍会影响SAR图像的聚焦性能，使SAR脉冲响应函数主瓣展宽、旁瓣升高，引起目标位置在距离向和方位向出现偏差，有必要对相位误差进行更精确的补偿。

3.2 基于变步长多维搜索的对比度增强相位校正方

法

假设包络已经完全校正，对此时的相位历史数据s~(m,n)沿方位向补偿相位误差Δφ(n)，并作方位IFFT之后，得到新的聚焦图像，记作f(m,h)，则

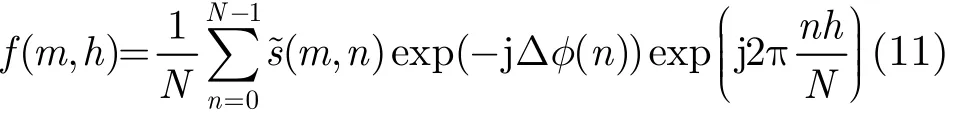
其中m=0,1,…,M−1, n=0,1,…,N −1,h=0,1,…, N−1。对比度[12]可以定义为图像中所有距离单元数据的方差和均值之比，然后取数学平均所得的结果，即

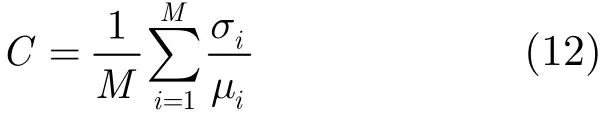
其中。一般来说，SAR图像的对比度越大，其聚焦效果越好。通过建立相位误差和SAR图像对比度之间的函数关系，采用CGA迭代求解对比度最大时的相位误差值，将其作为估计出的相位误差，对相位历史数据进行补偿。这样，相位估计问题就等价于如式(13)所示优化问题：

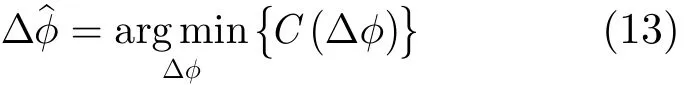
对比度函数是非线性函数，用于衡量相位误差对SAR图像局部区域的影响，而且它并不是相位误差的凸函数，因此并不一定具有全局最大值，但我们可以让它收敛于局部最大值。根据CGA，对比度C对相位误差φ(n),n=0,1,…,N −1的导数[12]可以表示为

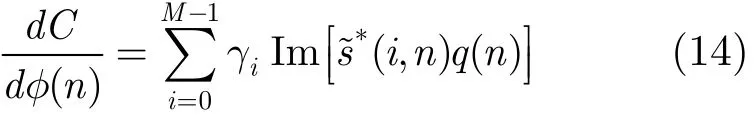
其中

由于SAR图像对比度局部极大值的密度非常高，为了找出正确的相位误差，必须附加特定的约束条件，改变优化策略[12]。如果我们一开始就将相位误差中的每个元素看作一个独立变量，即便算法的初值设置接近正确的解，我们仍然会发现利用CGA估计出的相位误差是错误的。因此，在利用CGA求解过程中，设计了一种变步长多维搜索的优化策略，克服算法本身特性对估计结果的影响。

首先，将整个优化过程分成不同的阶段，在每个阶段内，根据CGA迭代求解相位误差的中间结果，并将其作为下一个阶段估计的初始值。在该子问题收敛之后，需要减小块的大小以增加独立变量的个数，不断重复该过程，直至最后一个阶段，即独立变量的个数增加到图像的方位点数。在迭代求解不同阶段相位误差的过程中，并不是迭代次数越大越好，这是因为在实际中，相位误差的变化是一个连续缓慢变化的过程，太多次数的迭代结果很可能会造成邻近的方位单元之间的相位误差变化较大，整个的相位误差曲线并不平滑，这与实际情况并不相符[12]。一般设计5次左右的迭代次数就能得到较好的效果。

3.3 处理流程图

为了更清晰地表示本文提出的基于混合多阶段参数化最小熵RCM校正和基于变步长多维搜索的对比度增强相位校正方法操作步骤，此处给出详细的运算流程，如图2所示。

4 实验验证

本部分通过仿真实验和实测数据验证本文算法的有效性和实用性。

4.1 仿真实验验证

图2 本文算法流程图

实验1 在X波段聚束SAR回波数据的采集过程中，沿方位向加上大小为+15的运动误差，其中tm表示方位时间，仿真参数如表1所示。采用PFA算法对场景中心点的回波数据进行处理，距离脉冲压缩后的信号包络如图3(a)所示。与PFA插值前相比，经PFA 2维插值、距离IFFT后，相位历史数据的包络会发生变化。由RCM粗估计所得信号的包络如图3(b)所示，此时残余的RCM仍超过了一个距离单元，这就需要对残余RCM进行更高精度的校正。通过混合多阶段参数化最小熵方法校正后的信号包络如图3(c)所示。此时，信号的包络在一个距离单元内，说明了该方法能够较好地补偿信号的包络误差。

实验2 采用表1所示参数，但在数据采集时不加误差，采用PFA处理，经2维插值后，作距离向IFFT，得到相位历史域数据。在此处对该数据加沿方位向的相位误差，如图4(a)所示，采用PGA算法[6]估计相位误差所得结果如图4(b)所示。相应地，采用基于变步长多维搜索的对比度增强相位校正方法估计相位误差所得结果如图5(b)所示。

从图4(b)可以看出，用PGA方法估计出的相位误差中明显包含一个线性分量，它不会影响图像的聚焦性能，但会使图像发生整体偏移。图5(b)表明用CE方法估计出的相位误差与实际所加相位误差几乎只相差一个常数相位项，在SAR成像过程中，常数相位对最终图像的聚焦没有影响。图4(c)表示用PGA算法进行相位补偿后的点目标方位向脉冲响应剖面图，脉冲响应函数中心位置发生了偏移，相应的峰值旁瓣比和积分旁瓣比分别为-12.06 dB和-9.34 dB，图5(c)表示用CE方法进行相位补偿后的点目标方位向脉冲响应剖面图，积分旁瓣比和峰值旁瓣比分别为-13.39 dB和-9.88 dB。仿真结果表明，利用本文方法进行自聚焦后点目标的方位向聚焦效果得到了显著的提高，且聚焦性能优于PGA算法。

4.2 实测数据验证

下面通过对某所录取的含有农田、植物等场景的实测数据进行处理，来验证本文算法的有效性。该数据包含8192个脉冲回波，数据处理使用的距离向采样点数为4096。雷达工作在X波段，中心斜距约为40 km，距离/方位分辨率为0.5 m，录取数据的场景中无明显的孤立散射点，所采集数据的信噪比和对比度均较低。

图6(a)表示用本文方法进行自聚焦操作后，实测数据的聚焦效果图，图中垂直方向表示距离向，水平方向表示方位向。采用本文自聚焦方法处理后SAR图像的熵值和对比度分别为15.13和0.700，且场景中的农田、植物等聚焦良好，说明了本文算法能对低信噪比、低对比度场景的SAR数据进行良好的聚焦，具有很强的稳健性。为了定量评价本文算法对图像性能的改善情况，对图6(a)中矩形框内的点目标方位脉冲响应进行分析，如图6(b)所示。采用PGA方法处理得到的脉冲响应函数峰值旁瓣比和积分旁瓣比分别为-13.30 dB和-6.92 dB，而采用本文方法处理得到的相应结果分别为-12.86 dB和-10.06 dB。积分旁瓣比主要反映高频宽带相位误差的影响，积分旁瓣比越低，说明信号高频误差的补偿就越精确。显然，本文方法聚焦的点目标响应函数旁瓣更低、脉冲响应函数的形式更理想，充分说明了本文算法的有效性和必要性。

5 结论

本文算法可以有效、高精度地补偿惯导精度不足导致的RCM和相位误差，尤其是对低信噪比场景，如沙漠、草场等具有很好的聚焦性能和稳健性。仿真实验和实测数据验证了本文方法的有效性和精确性。文中的自聚焦方法是基于运动误差非空变假设，实际大场景成像中有可能难以满足，此时可考虑采用距离分块处理，保证假设精度。

图3 混合多阶段参数化最小熵算法校正包络误差的结果

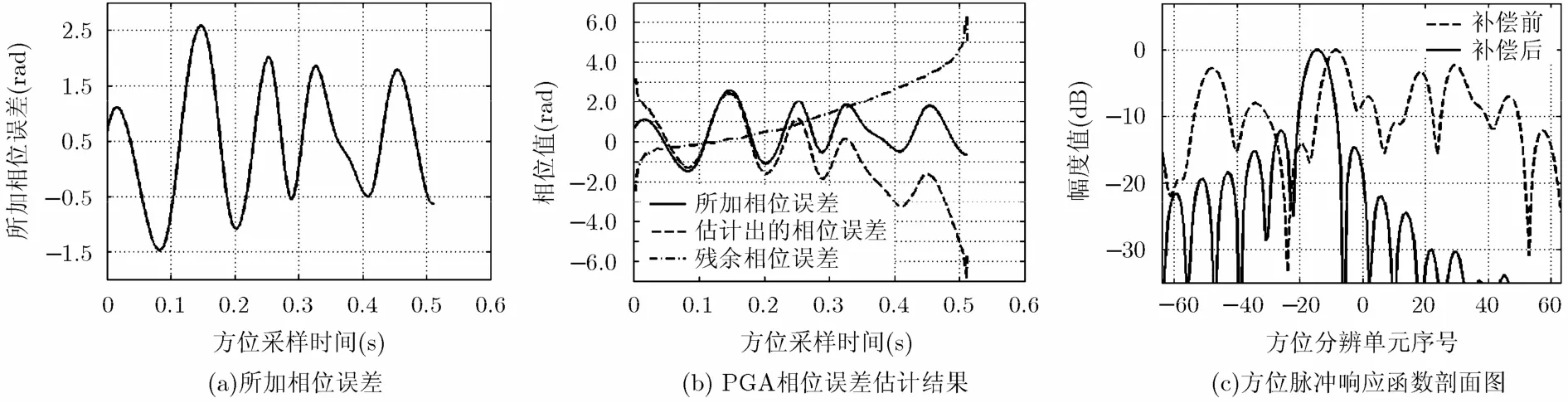
图4 PGA处理结果

图5 CE处理结果

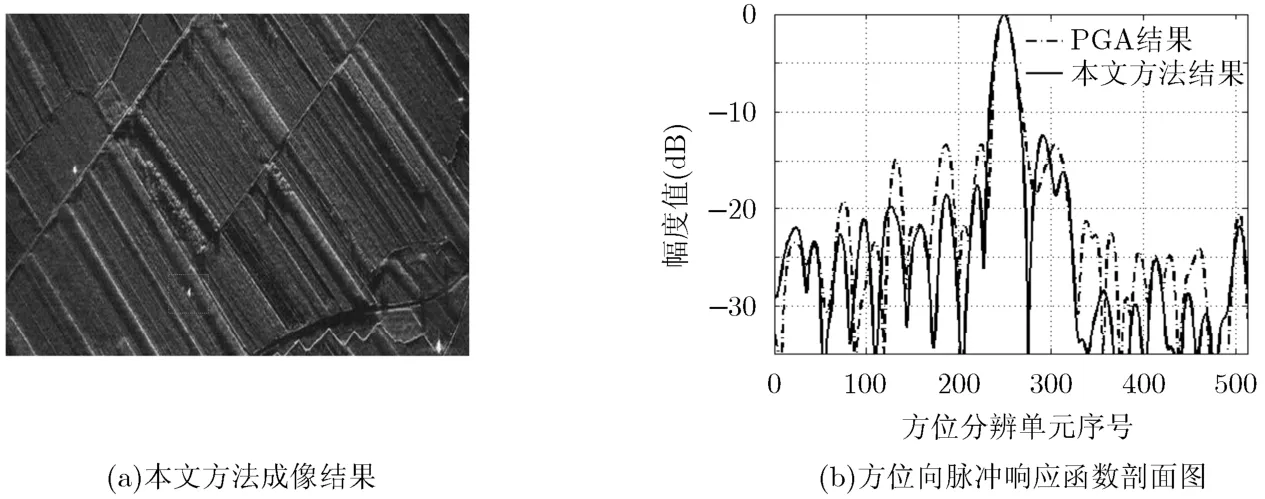
图6 本文方法处理结果

[1] 张磊. 高分辨SAR/ISAR成像及误差补偿技术研究[D]. [博士论文], 西安电子科技大学, 2012.

Zhang Lei. Study on high resolution SAR/ISAR imaging and error correction[D]. [Ph.D. dissertation], Xidian University, 2012.

[2] Yang Lei, Xing Meng-dao, Wang Yong, et al.. Compensation for the NsRCM and phase error after polar format resampling for airborne spotlight SAR raw data of high resolution[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 165-169.

[3] Carrara G, Goodman S, and Majewski M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithm[M]. Boston, MA: Artech House, 1995: 200-244.

[4] Xu Gang, Xing Meng-dao, Zhang Lei, et al.. Robust autofocusing approach for highly squinted SAR imagery using the extended wavenumber algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 5031-5046.

[5] 黄大荣, 张磊, 邢孟道, 等. 基于加权最大范数的SAR自聚焦方法[J]. 电子与信息学报, 2014, 36(1): 202-208.

Huang Da-rong, Zhang Lei, Xing Meng-dao, et al.. A weighted maximize norm method for SAR autofocus[J]. Journal of Electronics & Information Technology, 2014, 36(1): 202-208.

[6] Wahl D E, Eichel P H, Ghiglia D C, et al.. Phase gradient autofocus-a robust tool for high resolution phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-835.

[7] Ye Wei, Yeo T S, and Bao Zheng. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2487-2494.

[8] Xiong Tao, Xing Meng-dao, Wang Yong, et al.. Minimumentropy-based autofocus algorithm for SAR data using Chebyshev approximation and method of series reversion, and its implementation in a data processor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3): 1719-1728.

[9] Gao Yang, Yu Wei-dong, Liu Ya-bo, et al.. Sharpness-based autofocus for stripmap SAR using an adaptive-order polynomial model[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6): 1086-1090.

[10] Doerry A W. Autofocus correction of excessive migration in synthetic aperture radar images[R]. Sandia Laboratory, 2004.

[11] Thomas K J and Alaa K A. Monotonic iterative algorithm for minimum-entropy autofocus[C]. IEEE International Conference on Image Processing, Atlanta, USA, 2006: 645-648.

[12] Josse K. Image reconstruction and restoration using constrained optimization algorithms[D]. [Ph.D. dissertation], Purdue University, 1996.

曾乐天： 男，1988年生，博士生，研究方向为插值类SAR成像算法和运动补偿.

梁 毅： 男，1981年生，副教授，研究方向为SAR成像算法、SAR运动补偿.

邢孟道： 男，1975年生，教授，研究方向为SAR/ISAR成像及运动补偿、动目标检测、天波超视距雷达信号处理.

Autofocus Algorithm of High Resolution SAR Based on Polar Format Algorithm Processing

Zeng Le-tian Liang Yi Xing Meng-dao
(National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China)

Equipped with an airborne spotlight SAR, inertia navigation system can not measure the motion errors with the required accuracy for high resolution SAR imaging, which may degrade severely the quality of a SAR image. In this paper, a novel autofocus algorithm that can be directly embedded in Polar Format Algorithm (PFA) is proposed, that is, a Hybrid Multistage Parameterized Minimum Entropy (HMPME) algorithm to proceed Range Cell Migration (RCM) correction and a scaled-stepsize iterative phase correction method based on Contrast Enhancement (CE). The autofocus processing accurately compensates the effects of range cell migration and phase errors. Also, this algorithm is most robust in processing images of low contrast and low signal-to-noise ratio. Finally, simulations and experiments with real spotlight SAR data validate the effectiveness of the proposed algorithm.

SAR; Polar Format Algorithm (PFA); Autofocus; Parameterized minimum entropy; Contrast enhancement

TN957.52

： A

：1009-5896(2015)06-1409-07

10.11999/JEIT141131

2014-08-27收到，2014-12-08改回

中央高校基本科研业务费专项资金(K5051302046)和国家自然科学基金优秀青年基金(61222108)资助课题

*通信作者：曾乐天 zengletianlxm@gmail.com