Alpha稳定分布噪声下基于柯西分布的相位键控信号码速率最大似然估计
2015-07-12敏姬红兵
金 艳 朱 敏姬红兵
(西安电子科技大学电子工程学院 西安 710071)
Alpha稳定分布噪声下基于柯西分布的相位键控信号码速率最大似然估计
金 艳 朱 敏*姬红兵
(西安电子科技大学电子工程学院 西安 710071)
针对现有的相位键控(PSK)编码信号码速率估计方法在Alpha稳定分布中性能严重退化的问题,该文提出一种基于柯西分布的码速率最大似然估计(CMLE)新方法,该方法可同时估计码速率与定时偏差。CMLE利用窗口法将信号划分为定时偏差窗和多个宽度一定的非重叠且已同步的时域窗,每个窗只包含一个码元符号;在Alpha稳定分布噪声下,利用窗中符号信息构造了基于柯西分布的似然函数,可同时获得定时偏差窗宽与码元符号窗宽的最大似然估计。仿真结果表明,该方法能有效抑制Alpha稳定分布噪声并具有良好的参数估计性能。
信号处理;Alpha稳定分布;柯西分布;相位键控编码信号;码速率;最大似然估计(MLE)
1 引言
相位键控(Phase Shift Keying, PSK)编码信号具有抗干扰性强,保密性好等优良性能,是通信系统中的常用信号,其参数估计是电子对抗中的研究热点[1]。码速率能表征PSK信号的编码特性,因此,码速率的估计是PSK信号处理的重要一环。高斯分布满足中心极限定理,且易于处理和分析,在传统的PSK信号的码速率估计中,一般假设背景噪声服从高斯分布。然而,在实际噪声或杂波环境中,如闪电,海杂波,低频大气噪声等均具有很强的冲激特性。在这类脉冲噪声下,基于高斯噪声模型的常规处理方法性能退化甚至失效。Alpha稳定分布是描述此类非高斯脉冲噪声的一种有效模型,与高斯分布相比,其具有更厚的统计拖尾和显著的脉冲特性[2−4]。
针对PSK信号的码速率估计,目前已有多种有效的分析方法。文献[5]提出的时域自相关法,对接收信号做自相关处理,通过提取峰值估计信号的码速率,但该方法在相关积分时间选取较大时,运算量明显增大。文献[6,7]提出的循环谱相关估计法和循环自相关法,计算信号的循环统计量,并检测离散谱线,即可估得信号的码速率,但当噪声中存在幅值较大的分量时,基于循环统计量的二阶方法性能严重退化。文献[8,9]提出的基于相位差分和基于小波变换的码速率估计方法,对于噪声的抑制作用较低,在信噪比较高时才能获得参数的准确估计。文献[10]通过建立最大似然函数,求取极值获得码元信息,但该方法需要定时偏差等先验信息。此外,上述方法是以高斯噪声为背景的分析与处理,在Alpha稳定分布噪声背景下均失效。
针对Alpha稳定分布噪声下,传统的相位编码信号码速率估计失效的问题,本文提出一种基于柯西分布的码速率估计方法。该方法利用窗口法将接收信号划分为定时偏差窗和多个宽度一定的非重叠且已同步的时域窗,每个窗只包含一个码元符号信息。利用码元符号信息,构造基于柯西分布的最大似然函数,即可估计信号的码元宽度即码速率。
2 信号和噪声模型
设观测信号为x(t)=s(t)+v(t),其中相位编码信号[11]s(t)可表示为式中,f为载频,ϕ0为初相,ϕ(t)为相位编码调制序列。
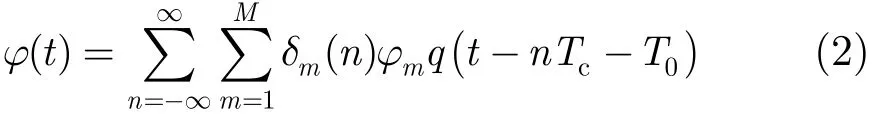
其中{ϕm}为信号符号集,δm(n)=δ(n),m =1, 2,…,M, δ(⋅)为离散Dirac函数,T0为定时偏差,Tc为码片时宽。当M=2,相位ϕ1和ϕ2的间隔为π时,s(t)为二进制相位键控(Binary Phase Shift Keying, BPSK)编码信号;当M=4,相位之间的间隔为π/2时,s(t)为四进制相位键控(Quaternary Phase Shift Keying, QPSK)编码信号。q(t)=。v(t)为加性Alpha稳定分布噪声[12]。观测信号离散采样点为t=nTs, Ts为采样周期。
一般情况下,Alpha稳定分布的概率密度函数(Probability Distribution Function, PDF)没有统一的封闭表达式,通常采用特征函数描述:

其中
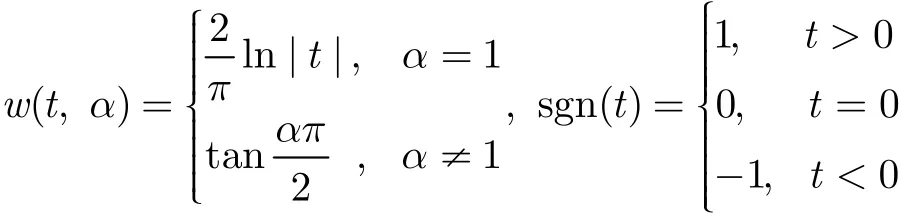
是符号函数。参数α为特征参数,表征PDF的尖锐程度与拖尾厚重程度,α值越小,PDF曲线越尖锐且拖尾越厚。参数γ>0为分散系数,又称为尺度系数,与高斯分布的方差类似。−1≤β≤1为对称参数,β=0为对称Alpha稳定分布(Symmetric α-Stable, SαS)。当α=1,β=0时对应为柯西分布[13];当α=2, β=0时对应为高斯分布,且柯西分布与高斯分布均具有封闭形式的PDF。−∞<a<+∞为位置参数,对于SαS, 0<α<1时,则a表示中值,1<α≤2时,则a表示均值。若满足a=0且γ=1,则Alpha稳定分布称为标准Alpha稳定分布。Alpha稳定分布噪声不具有统一封闭形式的PDF,但可通过特定的算法仿真体现。图1与图2分别表示不同α值下标准SαS的PDF曲线和时域分布,由图可知,α值越小,PDF曲线越尖锐且拖尾越厚重,时域表现为大幅度样本即大脉冲出现的概率越大。另外,当α=1时对应于标准柯西分布,其PDF曲线尖锐,拖尾较为厚重,时域冲激特性明显。此外,理论研究证明对于Alpha稳定分布噪声,仅当阶数p小于其特征指数α的统计矩是有限的[12]。因此,传统的基于二阶统计量的信号处理方法在Alpha稳定分布噪声下性能严重退化甚至失效。
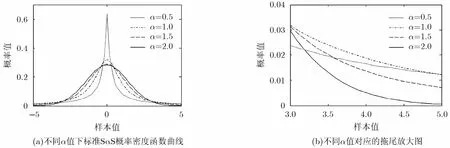
图1 标准SαS概率密度函数曲线

图2 不同α值下标准SαS的时域分布
3 基于柯西分布的码速率最大似然估计
3.1 柯西分布噪声下信号的PDF
柯西分布具有封闭形式的PDF,且其PDF曲线拖尾厚重,冲激特性明显,是Alpha稳定分布噪声的典型代表。已有许多学者提出在柯西分布噪声下的信号处理方法,并将其推广至一般的Alpha稳定分布噪声情况,分析并验证了其具有较好的性能,如基于最大似然位置估计的Myriad[14]和Meridian[15]滤波器等。为便于分析,本文推导了基于标准柯西分布的PSK信号码速率的最大似然估计,且仿真实验证明,该方法可应用于一般的Alpha稳定分布噪声情况。标准柯西分布为满足参数1,1, α=γ=
β=0,a=0的Alpha稳定分布,其 PDF为
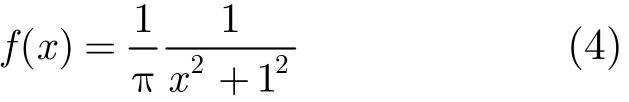
标准柯西分布噪声下,码元符号ϕm, m∈{1,2,…,M}的信号模型可表示为y=ϕm+v ,其中v为标准柯西分布噪声,则y的PDF为
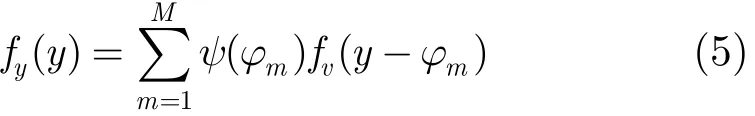
式中,fv(y)为标准柯西分布的PDF, ϕm为独立同分布序列,其概率满足ψ(ϕi)=ψ(ϕj)=1/M,i,j∈{1,2,…,M}且。
3.2 码速率的最大似然估计
设标准柯西分布噪声下,观测到的PSK信号为Sr={s0,S}={s0,s1,s2,…,sK},其中,s0表示定时偏差窗内的信号,S={s1,s2,…,sK}={s(1),s(2),…,s(N)}
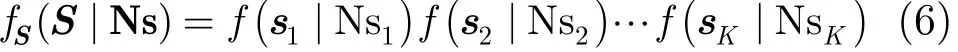
下面以BPSK信号为例,阐述信号窗口的划分。如图3所示,s0表示定时偏差窗内的信号,其宽度为NT0; si表示BPSK信号中第i个窗内的同步信号,Nsi表示信号si的宽度,Ns={Ns1,Ns2,…,NsK}为同步信号窗口宽度集合。为K个码元符号窗内信号,其PDF为
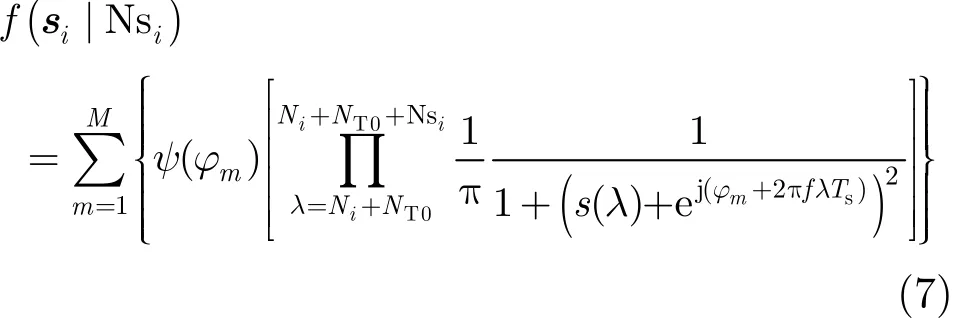
由式(5)可推得信号分量si的PDF为式中,NT0表示定时偏差窗宽,在非协作方式下所截获到的信号,其定时偏差一般不为0。表示前i−1个窗内的信号采样点数之和。其中M表示调制进制数,M=2时, ϕm∈{0,π}, ψ(ϕm)=1/2; M=4时;ϕm∈{π/4,3π/4,5π/4,7π/4}; ψ(ϕm) =1/4。将式(7)代入式(6)并取对数,可得信号S的对数似然函数
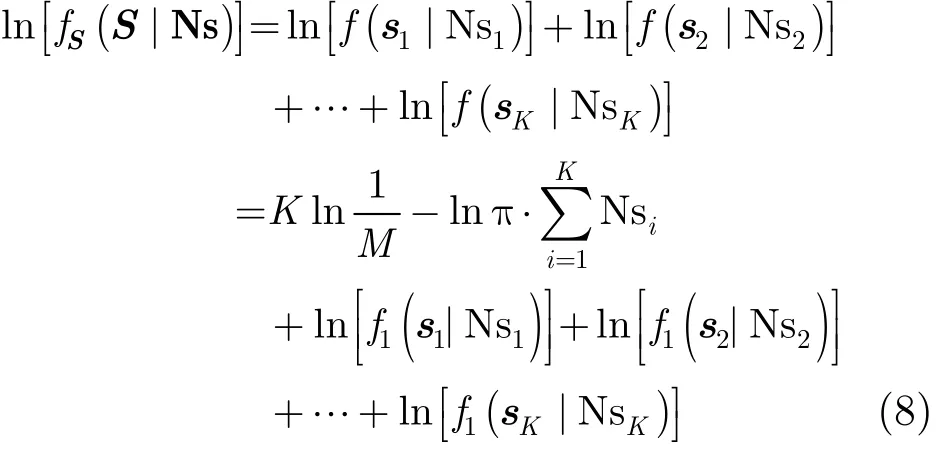
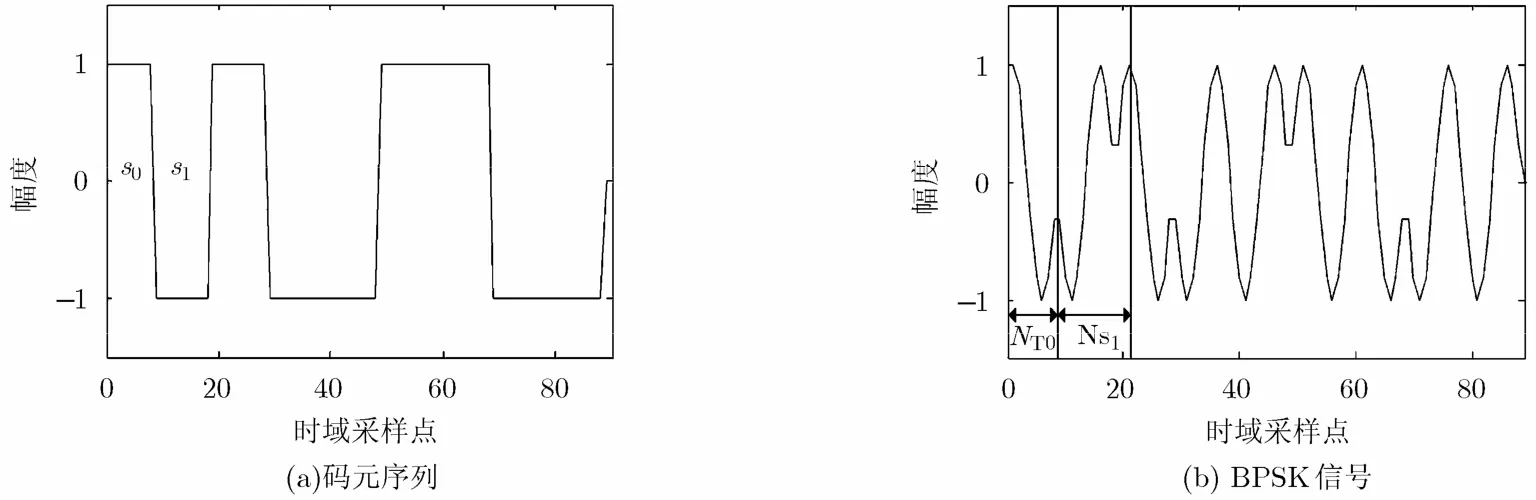
图3 无噪声情况下码元符号及其对应的BPSK信号
设每个码元内的平均采样点数为Ns,则Ns=Tc/Ts,且K⋅Ns=N,对于给定的Ns,则Nsi均可唯一确定,特别地,当Ns为整数时,Ns=Nsi=Nsj,i,j∈{1,2,⋅⋅⋅,K}。因此,在已知信号载频f后,可由信号S的对数似然函数估计未知参数Ns, NT0
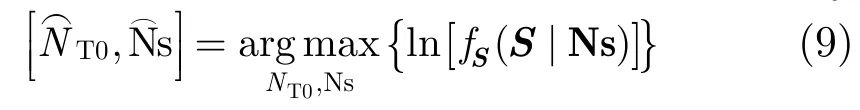

去除式(9)中的无关常数项可得需要注意的是NT0的取值范围与Ns的取值有关。因此,在由定时偏差窗宽NT0域和码元符号窗宽Ns域形成的2维平面(NT0,Ns)上进PSK信号的码速率c=1/(s⋅Ts)。行峰值搜索,^得到峰值所对应的2维坐标,即可估得s,则
4 仿真结果及分析
设PSK信号参数满足:观测时间T0=0.1 s,初相θ=0,采样频率fs=10 kHz,采样点数N=10000;其中,BPSK信号和QPSK信号的码元符号窗宽分别为Ns=6.6和Ns=6.9;定时偏差窗宽NT0=4。
仿真中噪声为加性标准SαS分布噪声,由于其不存在有限的二阶矩(α≠2.0时),使得方差的概念失去意义,因此采用广义信噪比[12]:

图4(a)和图4(b)分别为BPSK信号和QPSK信号在α=1.0, GSNR=0 dB的噪声下,2维平面(NT0,Ns)上取NT0=4的1维切片图。峰值所在位置分别为Ns=6.6, Ns=6.9,从而可估得信号的码速率。图4(c)和图4(d)分别为BPSK信号在α=1.0, GSNR=−3 dB和GSNR=−5 dB的噪声下的基于CML方法的切片图。
本文以归一化均方根误差(Normalized Root Mean Square Error, NRMSE)评价在Alpha稳定分布噪声下码速率估计方法的性能,并与基于循环自相关函数(Cyclic Autocorrelation Function, CAF)和基于Haar小波变换(Haar Wavelet Transform, HWT)的传统方法进行对比。假设Monte Carlo仿真实验的次数为R,所估计的参数为θ,第i次实验中的估计值为,则参数θ估计的归一化均方根误差为。
实验1 在不同的广义信噪比下,对BPSK信号经过200次Monte Carlo实验,所得结果如图5所示。由图可知,在α=0.5的Alpha稳定分布噪声下,当GSNR≥−3 dB , CMLE方法能准确估计码速率;在α=1.0和α=1.5的Alpha稳定分布噪声下,基于CMLE的方法分别在GSNR≥−4 dB和GSNR≥−5 dB时达到准确估计。HWT方法是基于一阶统计量的方法,利用Haar小波变换检测信号的相位突变点,从而获取信号码速率的估计。然而,在脉冲噪声下,大幅值脉冲导致检测误判。CAF的码速率估计是传统的基于二阶统计量的方法,α<2.0时其二阶矩不存在,因此,在脉冲噪声下,基于HWT和基于CAF的BPSK信号码速率估计方法均失效。在α=2.0的Alpha稳定分布噪声下,即高斯噪声下,上述3种方法均能有效估计码速率,在GSNR≥−7 dB时,基于CMLE的方法能准确估计码速率,基于CAF和基于HWT的方法分别在GSNR≥−8 dB 和GSNR≥−1 dB时,能达到准确估计。此外,基于CAF的方法算法复杂度为O(N2logN),本文方法的算法复杂度为O(2MN2)。
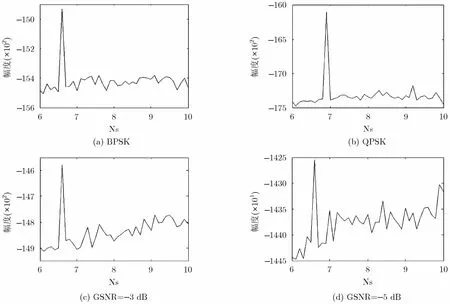
图4 NT0=4的1维切片图
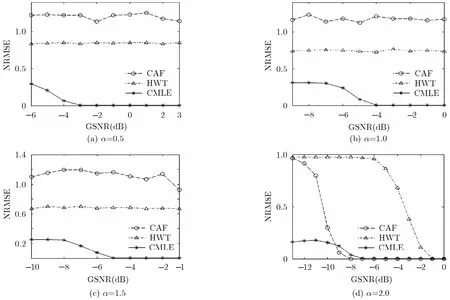
图5 BPSK信号码速率估计性能比较
2由此表明,在样本数较大时,本文方法算法复杂度较CAF方法低,且在信噪比较低的脉冲噪声和高斯噪声环境下均可准确估计BPSK信号的码速率。
实验2 在不同的广义信噪比下,对QPSK信号经过200次Monte Carlo实验,所得结果如图6所示。由图可知,在α=0.5的Alpha稳定分布噪声下,当GSNR≥2 dB, CMLE方法能准确估计码速率;在α=1.0和α=1.5的Alpha稳定分布噪声下,基于CMLE的方法在GSNR≥1 dB时可达到准确估计。由于脉冲噪声的影响,基于CAF和基于HWT的QPSK信号码速率估计方法均失效。在α=2.0的Alpha稳定分布噪声下,即高斯噪声下,上述3种方法均能有效估计QPSK信号码速率,在GSNR≥−1 dB时,基于CMLE的方法能准确估计码速率,基于CAF和基于HWT的方法分别在GSNR≥−7 dB和GSNR≥0 dB时,能达到准确估计。基于CMLE的方法是以柯西分布噪声为背景的码速率估计方法,对于脉冲噪声抑制作用较强,而在高斯噪声下,基于CAF方法的参数估计性能优于基于CMLE的方法。
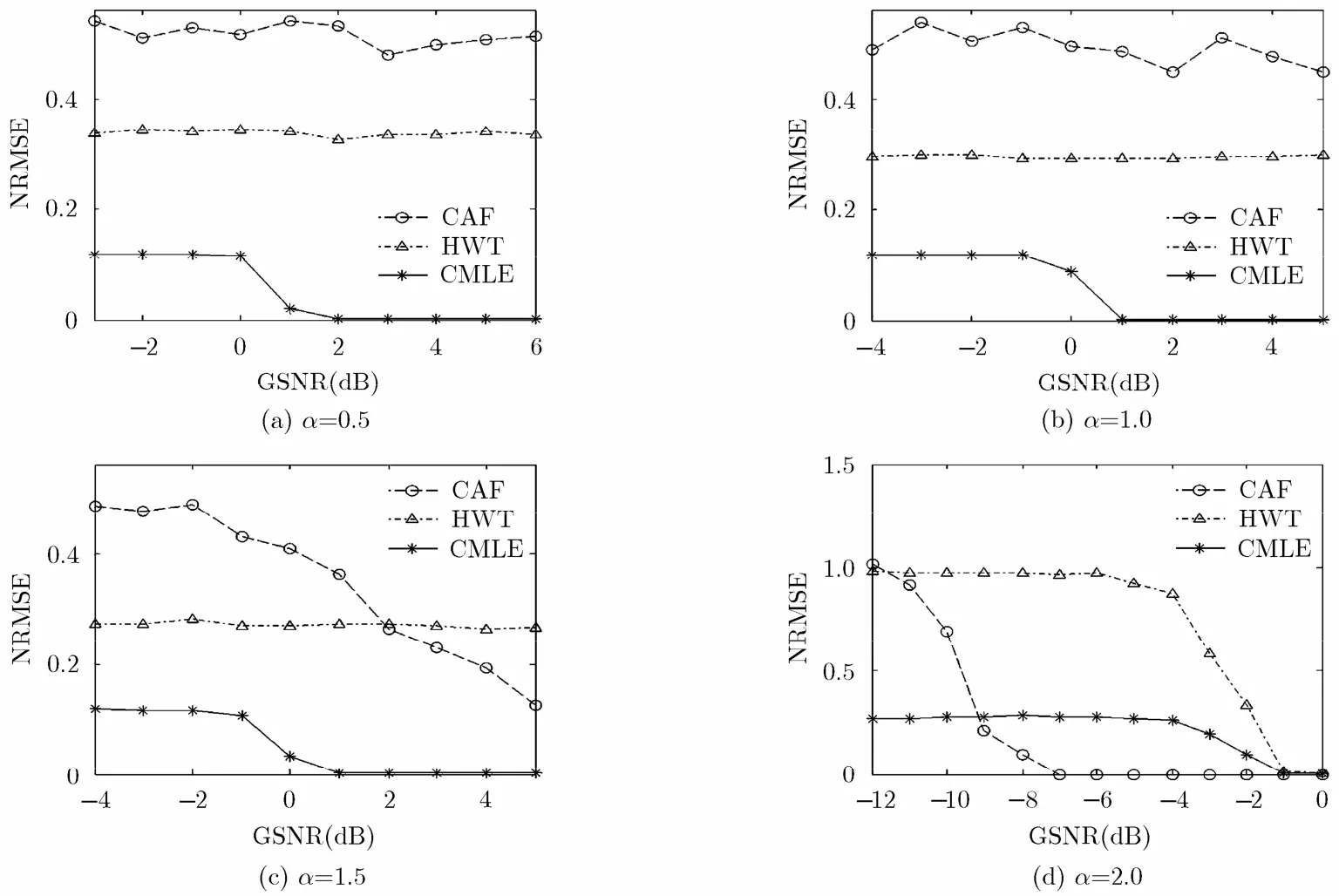
图6 QPSK信号码速率估计性能比较
5 结束语
在Alpha稳定分布噪声下,本文提出了一种基于柯西分布的PSK信号码速率最大似然估计算法,并给出了算法步骤。该方法通过窗口划分将信号分为定时偏差窗与码元符号窗,并利用码元符号信息,建立基于柯西分布的似然函数。在Alpha稳定分布噪声下,可同时获得定时偏差窗宽与码元符号窗宽的最大似然估计,从而得到码速率的估计。仿真实验中,分别对BPSK和QPSK信号进行码速率的最大似然估计,并对比了基于循环自相关函数与基于Haar小波变换的参数估计方法。仿真结果表明,本文方法较基于循环自相关函数的方法算法复杂度低,且相对于Haar小波变换和循环自相关函数的方法,该方法对脉冲抑制作用强,在脉冲强度不同的Alpha稳定分布噪声下,均具有良好的参数估计性能。
[1] 曾维贵, 孙迎丰, 胥辉旗, 等. 准连续波体制雷达波形设计与参数选择[J]. 系统工程与电子技术, 2013, 35(3): 517-521.
Zeng Wei-gui, Sun Ying-feng, Xu Hui-qi, et al.. Waveform design and parameter calculation for quasi-continuous wave radar system[J]. System Engineering and Electronics, 2013, 35(3): 517-521.
[2] Tsakalides P and Nikias C L. Maximum likelihood localization of sources in noise modeled as a stable process[J]. IEEE Transactions on Signal Processing, 1995, 43(11): 2700-2713.
[3] Pelekanakis K and Chitre M. Adaptive sparse channel estimation under symmetric alpha-stable noise[J]. IEEE Transactions on Signal Wireless Communications, 2014, 13(6): 3183-3195.
[4] Francois-Xavier S, Dominique P, and Mathieu D. On symmetric alpha-stable noise after short-time Fourier transform[J]. IEEE Signal Processing Letters, 2013, 20(5): 455-458.
[5] 张天骐, 杨柳飞, 代少升, 等. DS信号伪码周期及码片速率估计的自相关法[J]. 航天电子对抗, 2007, 23(4): 53-57.
Liu Tian-qi, Yang Liu-fei, Dai Shao-sheng, et al.. Estimation of period and chip rate of pseudo-noise sequence for direct sequence spread spectrum signals using correlation techniques[J]. Aerospace Electronic Warfare, 2007, 23(4): 53-57.
[6] 张籽兵, 李立萍, 肖先赐. MPSK信号的循环谱检测及码元速率估计[J]. 系统工程与电子技术, 2005, 27(5): 804-806.
Zhang Zi-bing, Li Li-ping, and Xiao Xian-ci. Detection and chip rate estimation of MPSK signals based on cyclic spectrum density[J]. System Engineering and Electronics, 2005, 27(5): 804-806.
[7] 金艳, 姬红兵, 罗军辉. 一种基于循环统计量的直扩信号检测与参数估计方法[J]. 电子学报, 2006, 34(4): 634-637.
Jin Yan, Ji Hong-bing, and Luo Jun-hui. A cyclic-cumulant based method for DS-SS signal detection and parameter estimation[J]. Acta Electronica Sinica, 2006, 34(4): 634-637.
[8] 付琴琴. 相位编码信号的参数估计[D]. [硕士论文], 西安电子科技大学, 2012: 39-41.
Fu Qin-qin. Parameter estimation of phase-coded signals[D]. [Master dissertation], Xidian University, 2012: 39-41.
[9] Wang Long, Zhang Geng-xin, Bian Dong-ming, et al.. Blind symbol rate estimation of satellite communication signal by Haar wavelet transform[J]. Journal of Electronics (China), 2011, 28(2): 199-203.
[10] Carlos M, Sandro S, and Lopez-Valcarce R, Non-data-aided symbol rate estimation of linearly modulated signals[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 664-674.
[11] 张佳芬, 和小冬, 唐斌. 伪码-线性调频信号快速参数估计[J].电讯技术, 2009, 49(12): 100-103.
Zhang Jia-fen, He Xiao-dong, and Tang Bin. A fast parameter estimation approach for multiplicative signal combined PRBC and LFM[J]. Telecommunication Engineering, 2009, 49(12): 100-103.
[12] 赵新明. Alpha稳定分布噪声下调频信号参数估计研究[D]. [硕士论文], 西安电子科技大学,2014: 10-14.
Zhao Xin-ming. Research on parameter estimation of frequency-hopping signals in alpha stable noise[D]. [Master dissertation], Xidian University, 2014: 10-14.
[13] 杨少兵, 吴命利. 基于广义柯西分布的系统侧谐波阻抗估计[J]. 中国电机工程学报, 2014, 34(7): 1159-1166.
Yang Shao-bing and Wu Ming-li. An assessment method of power system harmonic impedance based on generalized Cauchy distribution[J]. Proceedings of Chinese Society for Electrical Engineering. 2014, 34(7): 1159-1166.
[14] Gonzalez J G and Arce G R. Optimality of the myriad filter in practical impulsive-noise environments[J]. IEEE Transactions on Signal Processing, 2001, 49(2): 438-441.
[15] 赵新明, 金艳, 姬红兵. α稳定分布噪声下基于Merid滤波的跳频信号参数估计[J]. 电子与信息学报, 2014, 36(8): 1878-1883.
Zhao Xin-ming, Jin Yan, and Ji Hong-bing. Parameter estimation of frequency-hopping signals based on Merid filter in αstable noise environment[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1878-1883.
金 艳: 女,1978年生,博士,副教授,硕士生导师,研究方向为现代信号处理、统计信号处理、信号检测与估计、通信信号侦测等.
朱 敏: 男,1991年生,硕士生,研究方向为信号检测与估计、脉冲噪声处理.
姬红兵: 男,1963年生,博士,教授,博士生导师,研究方向为光电信息处理、微弱信号检测与识别、医学影像处理等.
Cauchy Distribution Based Maximum-likelihood Estimator for Symbol Rate of Phase Shift Keying Signals in Alpha Stable Noise Environment
Jin Yan Zhu Min Ji Hong-bing
(School of Electronic Engineering, Xidian University, Xi'an 710071, China)
In order to solve the problem that the performance of existing algorithms for the symbol rate estimation of Phase Shift Keying (PSK) signals will significantly degrade in the Alpha stable noise environment, a novel Cauchy distribution based Maximum-Likelihood Estimator (CMLE) method for symbol rate of PSK signals is proposed. The parameters of the timing offset and the symbol rate can be estimated simultaneously through this method. The windowed procedure is utilized in the CMLE and the noise polluted PSK signal is divided into a timing offset window and the multiple windows with certain width which are non-overlapping and synchronized in the time domain, and only one code symbol is contained in each window; in the Alpha stable noise environment, the symbol in the window is utilized and a likelihood function based on Cauchy distribution is built, then the maximum-likelihood estimation of window width for the timing offset and the symbol rate can be achieved simultaneously. The simulation results show that the proposed method can suppress the Alpha stable noise efficiently and offer superior parameter estimation performance.
Signal processing; Alpha-stable distribution; Cauchy distribution; Phase Shift Keying (PSK) signals; Symbol rate; Maximum-Likelihood Estimator (MLE)
TN911.7
: A
:1009-5896(2015)06-1323-07
10.11999/JEIT141180
2014-09-10收到,2014-12-25改回
国家自然科学基金(61201286),陕西省自然科学基金(2014JM8304)和中央高校基本科研业务费专项资金(K5051202013)资助课题
*通信作者:朱敏 zhum91@163.com
