外界载荷对圆柱涡激振动能量转换的影响

王军雷，冉景煜，张智恩，张 力，蒲 舸，丁 林

（重庆大学 低品位能源利用技术及系统教育部重点实验室，重庆400044）

近年来，收集流体中微弱流动能是国内外广泛关注的热点.微小型风力收集装置能够在无人环境下将风能转化为电能并加以储存，同时具有体积小、持久性好以及可无人操控等特点，克服了大型风力装置的局限性，在环境保护、建筑安全以及交通系统中具有很高的实际应用价值.相比传统风力发电装置，压电悬臂梁流致振动能量收集器不需要复杂的结构、安装方便，且能量密度和功率谱密度相对较高.近年来，利用压电材料从涡激振动中收集能量的研 究工作 得 以 广 泛 开 展［1-3］.Allen等［4］设 计 了“eel（鳗鱼）”能量收集器，但是未给出具体发电效率和发电功率的计算方法.Taylor等［5］使用鳗鱼结构，模拟了压电结构与流场的耦合作用，但是没有给出输出电压和功率的计算方法.Kwon［6］采用多组锆钛酸铅（PbZrTi，PZT）安装在T 型结构上的能量收集方式，在15m／s的最高风速下获得4mW的输出功率.在压电能量收集理论研究方面，Mehmood等［7］使用机电耦合方法得出压电悬臂梁的能量收集能力与悬臂梁的振幅有关.Zhu等［8］针对压电能量收集装置（piezoelectric energy harvesting device，PEHD）的发电工作效率，通过对比三维及二维本构方程，得出悬臂梁发电模型的二维模型具有适用性，实现了数值模拟的降维.

涡激振动是一种流固交替耦合的自激振动过程.当旋涡脱落频率和结构固有频率相近时，会发生“锁定”现象［9］，振动振幅显著增大.Anagnostopoulos等［10］发现中等雷诺数下圆柱绕流涡激振动存在3个分支.在上支阶段，流速较低时，自振频率较小，此时自振频率逐渐接近圆柱自身固有频率，振幅逐渐增大，表现出“拍”现象，可视为过渡段；在锁定阶段，自振频率与固有频率发生耦合同步现象，振幅显著增大，振动能与自振频率较高；在下支阶段，出现与上支类似的运动规律，但与上支不同的是，此时圆柱的振幅较小，自振主频率增大并逐渐解除与固有频率的耦合作用.利用“锁定”时系统振动能较大的特点，Bernitsas等［11-12］提出了一种海洋清洁能源收集装置（vortex-induced vibration aquatic clean energy，VIVACE），并在此基础上利用计算流体力学（CFD）技术［13-14］对其进行能量收集评估，从而实现利用涡激振动原理收集海洋流动能，并给出海洋流动能收集的表达式［12］：

式中：P 为功率，ρ为流体密度，Cy为柱体表面升力，fo为自振频率，ym为振动振幅，D 为圆柱直径，L为圆柱体的长度，φ 为相位角.从式（1）可以看出，系统的输出功率与圆柱的振动振幅有着直接关系.Wu等［13-14］利用OpenFOAM 针对单圆柱和多圆柱的涡激振动问题开发了求解器.Molino-Minero-Re等［15］提出了一种可用于在水槽中收集涡激振动能的旗帜状柔性结构，并指出输出功率与振幅呈正比.

上述研究大多未充分解决流体-结构-电路（流-固-电）三相耦合的问题，并认为系统输出功率与振动振幅成正比关系.而涡激振动能量收集回路是通过加入载荷实现利用电路载荷进行能量收集，外界载荷对涡激振动系统具有负反馈作用，因此必须考虑电路与涡激振动的机电耦合效应.解决三相耦合问题的关键在于计算外界载荷对系统能量输出的影响.

本研究通过在Matlab，中使用矩阵法计算载荷对涡激振动系统阻尼和固有频率的影响，计算出电压输出的准稳态解，并以上述结果为基础利用OpenFOAM 平台计算圆柱涡激振动质量-弹簧-阻尼系统流固耦合响应.重点研究外界载荷对涡激振动系统振幅、电压输出以及功率输出性能的影响，为涡激振动的能量收集提供理论基础.

1 物理模型

1.1 质量-弹簧-阻尼系统

为描述涡激振动能量转换模型中的刚性圆柱运动，取物理模型如图1（a）所示，在圆柱两端使用2根细长的PZT 压电薄片进行支撑，将带有电阻的电路连接到PZT 压电悬臂梁上用于收集电荷.忽略圆柱横向振动时压电片的旋转自由度，近似为二维单自由度质量-弹簧-阻尼（M-C-K）系统，如图1（b）所示.其中M 为系统质量，C 为系统阻尼，K 为系统的弹簧刚度，无量纲来流速度取折合速度（reduced velocity）Ur＝U／（ωn·D）［9］，其中U 为来流风速，ωn为圆柱的固有频率，D 为圆柱直径.

1.2 网格划分与边界条件

本研究采用的流体计算域大小为50D×50D，圆柱位于流场正中心.边界条件为速度进口，压力出口，壁面采用无滑移边界条件.计算区域上下边界距离圆柱足够远，边界对柱体周围流场的影响可以忽略［16］，因此上下边界采用与进口相同的边界条件，从而保证流场流动的均匀性.控制边界为

式中：Ω 为流固耦合面的外表面，V 为柱体的移动速度，VΩ为流固耦合面的移动速度.在流固耦合计算过程中，柱体在流场边界范围中上下移动.

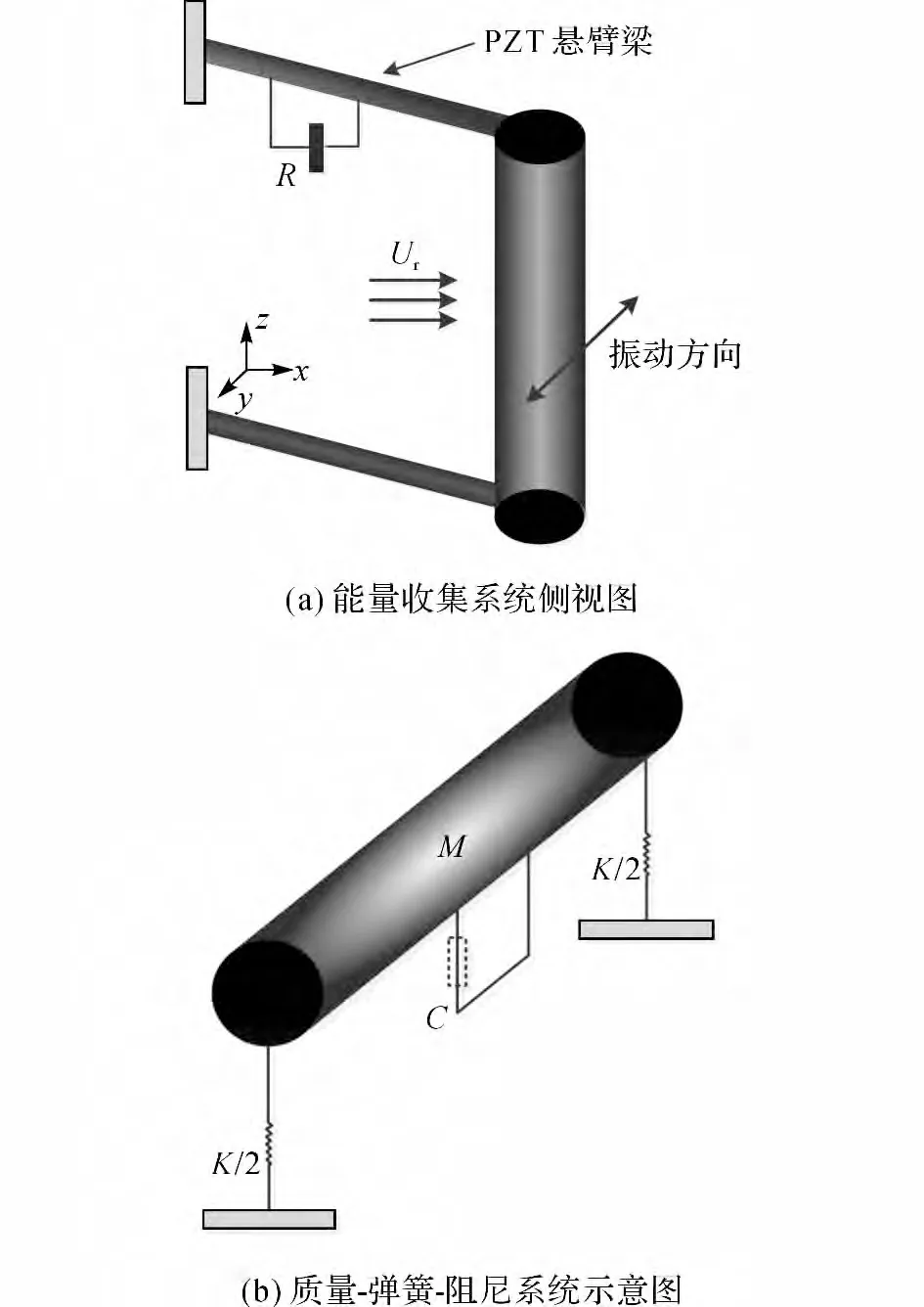
图1 能量收集系统与振动系统Fig.1 Energy harvesting system and vibrating system

在计算涡激振动时，动网格的处理是影响计算效率及计算精度的重要因素之一.当涡激振动发生时，圆柱上下移动.同时，如图2所示，计算区域网格随圆柱发生整体运动，克服了传统动网格的网格扭曲及变形的问题，从而提高计算效率和计算精度.采用Gambit生成四边形网格，并在Re＝150时采用3种不同网格进行网格无关性验证，结果如表1 所示，其中CL、CD、St分别为升力系数，阻力系数和斯特劳哈尔数.从表1可以看出，3种网格的计算结果较为吻合，因此选取网格密度为中等的网格来保证网格计算具有无关性.

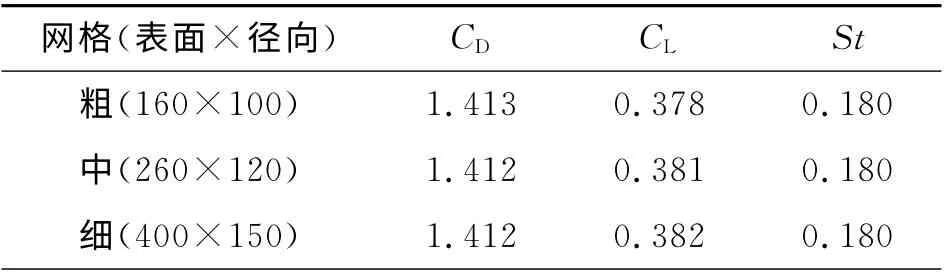
表1 网格无关性验证（Re＝150）Tab.1 Neutrality authentication of meshes（Re＝150）

2 数学模型

为计算圆柱绕流外流场、涡激振动和电路回路3种不同量场的耦合过程，使用Navier-Stokes方程描述外界流场的流动，使用二阶范德波尔方程描述单自由度M-C-K系统的涡激振动过程，最后使用高斯定律与振动方程的耦合形式描述机电耦合系统.

图2 计算所用网格示意图Fig.2 Schematic diagram of computational mesh

2.1 流固耦合模型

2.1.1 流动控制方程 圆柱绕流外部流场使用连续性方程和Navier-Stokes方程进行计算：

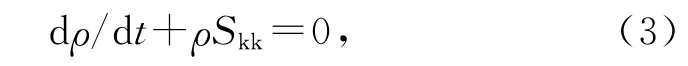
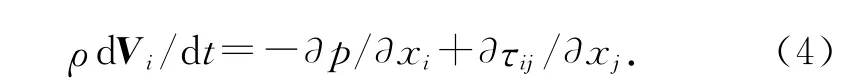
式中，p 为压强，ρ为流体密度，Vi为流体速度矢量，τij为应力张量，Skk为应变率张量.

2.1.2 单自由度范德波尔振动方程 单自由度MC-K系统的运动控制方程由二阶范德波尔方程表示：

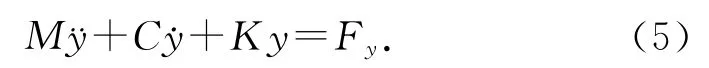
M、K、C 存在以下关系：

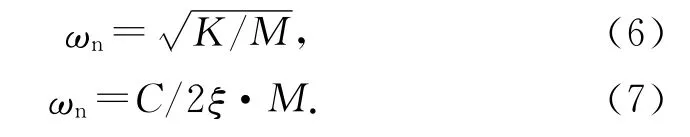
式中，Fy为垂直于来流方向的单位体积的流场力，ξ为无量纲阻尼比，y 表示柱体的振动位移，˙y和¨y分别表示位移的一、二阶导数.将范德波尔方程与流体控制方程在求解器中同时求解，可以得到圆柱的动态振动响应.

2.2 机电耦合模型

2.2.1 阻尼及固有频率求解 为了描述涡激振动电路中振幅与电压的关系，引入高斯定律［17］进行理论推导.将高斯定律与式（5）的机电耦合变形方程联立可得

式中：θ为机电耦合系数，Cp为电容系数，U 为电压，R 为电阻.

式（8）、（9）分别考虑了涡激振动系统对电路输出电压的影响，同时考虑电路对振动系统的负反馈作用，即机电耦合.结合流场计算结果，即可实现流-机-电三相耦合.

为求解载荷对系统阻尼和固有频率的影响，使用矩阵法求解二阶非线性常微分方程式（8）的线性方程以及式（9）［18］.

令：X1＝y，X2＝˙y，X3＝U，将式（6）、（7）代入式（9）、（10）得

将上述方程组表示为矩阵形式：

式中：X＝［X1，X2，X3］T，

矩阵B（R）X 有3 个不同的特征值ki（i＝1，2，3）.Barrero-Gil等［18］指出：矩阵B（R）X 的特征值中前2个特征值与无电路振动系统类似，而第3个特征值则是机电耦合效应产生的结果，如压电系统受到基础或气弹性激励的作用，且为常实负数.k1、k2存在共轭关系，其中共轭解的实部（real）和虚部（imaginary）分别表示机电耦合系统中的阻尼和固有频率；而由于k3是常实负数，本文在计算矩阵平凡解时仅考虑k1、k2的实部.

本研究选用文献［7］中的单自由度振动机电耦合系统参数，如表2所示.

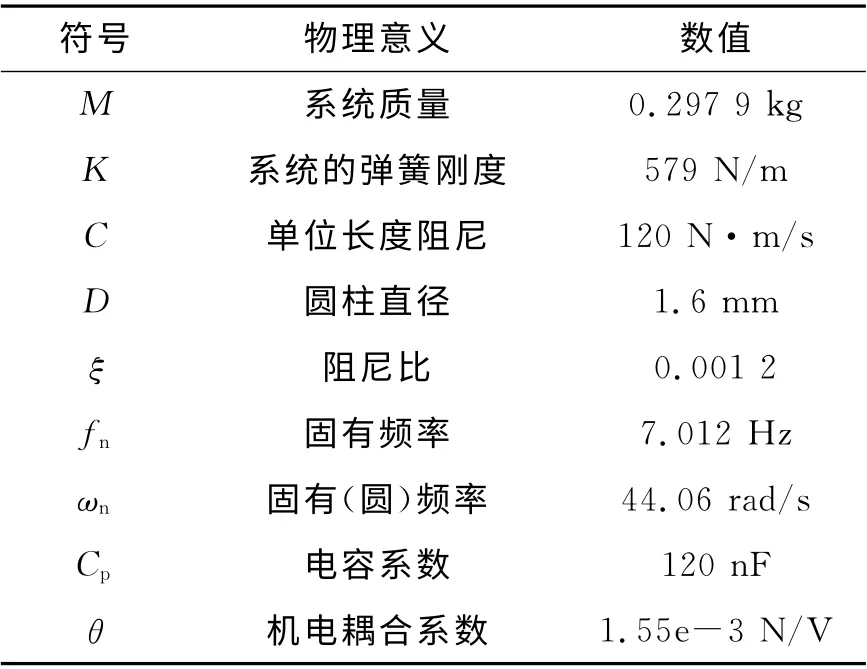
表2 单自由度振动机电耦合系统参数Tab.2 Parameters of free degree vibration electromechanical system

2.2.2 电压输出准稳态模型 采用Morse等［19］的准稳态模型描述涡激振动振幅，并用以计算随时间变化振动能量的收集.在涡激振动处于同步性区域时，在能量收集系统中，柱体的振动振幅可以表示为正弦波形式：

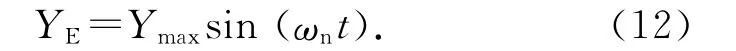
值得注意的是，电压时程与振动振幅时程曲线是同步的，并不存在相位差.本文重点计算电压输出的峰值，将式（12）代入式（10），在Matlab中求出电压的准稳态解解析式：

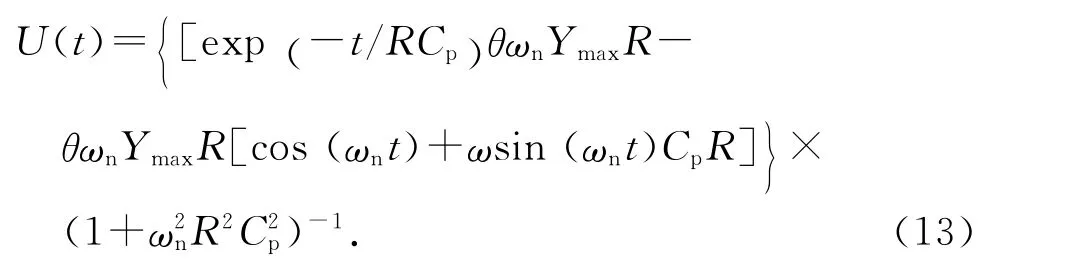
以上过程中的数学表达式包括流固耦合和机电耦合的求解过程.首先在OpenFOAM 中求解式（3）、（4），得出流场压强p.压强p 作用在柱体上产生流场力Fy.利用p 求解式（5），得到柱体产生的振动位移y.在压力影响柱体运动的同时，柱体在流场中的振动反作用于流场从而影响流场分布，如此交替计算即解决流固耦合问题.在机电耦合模型中求解方程组（8）、（9），可得出系统阻尼C、固有圆频率ωn的变化，而C 和ωn可以通过式（5）直接影响流固耦合计算中的P 和Fy.最后求得系统的振幅最大值Ymax，结合固有圆频率计算结果ωn，使用式（13）可以得出系统电压输出的时程曲线，以上即为流-固-电三相耦合全过程.

3 流体求解器验证

为了验证本文流固求解器的正确性，采用文献［10］中的实验参数（绕流柱体的质量与柱体排开的流体质的比值m＊＝149，ξ＝0.001 2）进行涡激振动计算，并将结果与数值模拟的文献结果［7，20-21］进行对比，如图3所示.

当94＜Re＜140 时，本文的计算结果与文献［7］、［20］及［21］中的数值模拟结果吻合较好.值得注意的是，本文得出的振幅值略小于文献［10］中的实验值，可能有2个方面的原因：一是本文采用的是无限大流动空间计算圆柱涡激振动，而文献［10］的实验过程中细长圆柱体的一部分在自由液面以上，存在自由液面的影响；二是文献［10］的研究中虽然圆柱细长比比较大，但是在圆柱底端未安装挡板，故实验测得涡脱频率偏小，涡激振动的上支过渡段会延迟进入锁定阶段.

图3 本文方法的计算结果与其他文献结果的对比Fig.3 Comparisons between results of present method and published data

4 计算结果及分析

4.1 系统阻尼和固有频率特性

通过Matlab软件求出机电耦合系统的阻尼和固有圆频率，共轭解的实部和虚部随电阻变化的计算结果如图4所示.

图4 矩阵共轭解实部、虚部随电阻的变化Fig.4 Variations of real and imaginary parts of conjugate solution with load resistance

根据电路共轭解实部与虚部的关系，结合图4可以看出，当载荷较小时，系统总阻尼较低.当R＜100kΩ 时，随载荷的增大，系统总阻尼逐渐升高；当R＝100kΩ 左右时，系统总阻尼达到最大值.此外，随载荷继续增大，由于机电耦合阻尼的压电分流阻尼效应（shunt damping effect）［22］，系 统 总 阻 尼 减小.在固有圆频率方面，当R＜30kΩ 时，频率基本保持在44rad／s；当R＞2 MΩ 时，频率基本保持在50rad／s以下.系统固有圆频率较为稳定，基本保持在44～50rad／s.

4.2 振幅变化特性

振动振幅是涡激振动机电耦合系统机电转换系统能力的重要参数.为充分考察载荷对系统机电耦合的影响，考察载荷值范围为1、10、100kΩ 以及1、10 MΩ 时振幅动态响应随雷诺数的变化情况.

如图5所示为当Re＝100时，不同载荷值对系统振动振幅的影响.由振幅时程曲线可以观察到振幅幅值随载荷值的变化而变化.当R＝1kΩ 时，振幅最大值为0.23D；当R＝10kΩ 时，振幅下降到y＝0.16D；当R＝100kΩ 时，振幅下降到0.09D；当R＝1MΩ 时，振动振幅增大；当R＝10MΩ 时，振幅最大值达到0.25D，超过当R＝1kΩ 时的峰值.振幅时程曲线的峰值总体呈现随载荷的增大先减小后增大的趋势.上述结果与图4中涡激振动阻尼随载荷的变化规律对应，系统阻尼越大，振动能越小，振幅相应越小.

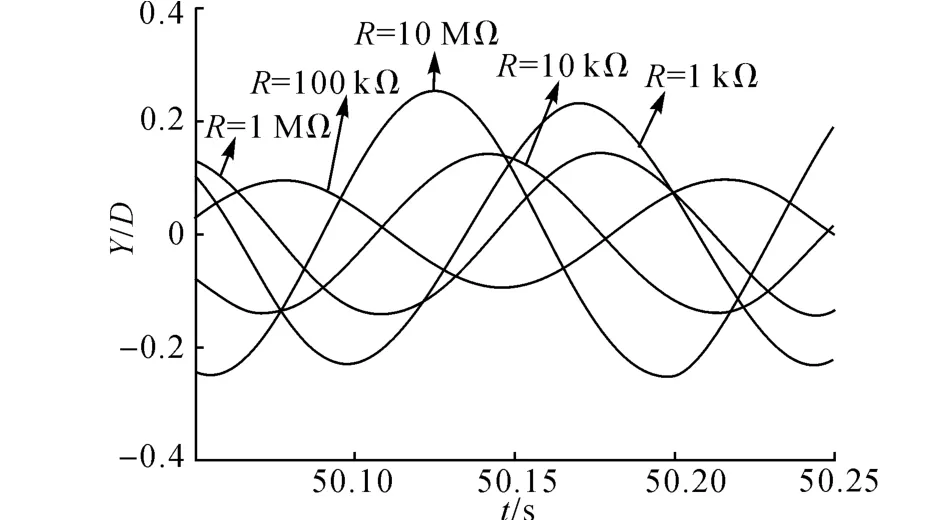
图5 不同载荷下的振幅时程曲线（Re＝100）Fig.5 Time histories of amplitude with different load resistances when Re＝100

如图6所示为当94≤Re≤115时不同载荷的振动幅值随雷诺数的变化情况.当R＝1kΩ 时，振幅在柱体进入锁定区后逐渐达到最大值0.31D.当Re增大时，振幅峰值开始下降，振幅曲线过渡到下支，振幅减小.当R＝10kΩ 时，锁定区域振幅最大值只有0.19D；而当R＝100kΩ 时，系统阻尼增大到峰值，此时振幅最大值达到0.135D；当R＝1 MΩ 时，随振动阻尼减小，振幅达到0.21D；当R＝10 MΩ时，振幅最大值达到0.34D.可见随载荷值的增大，振幅曲线先增大后减小.当98＜Re＜103 时，系统具有较大振幅值.

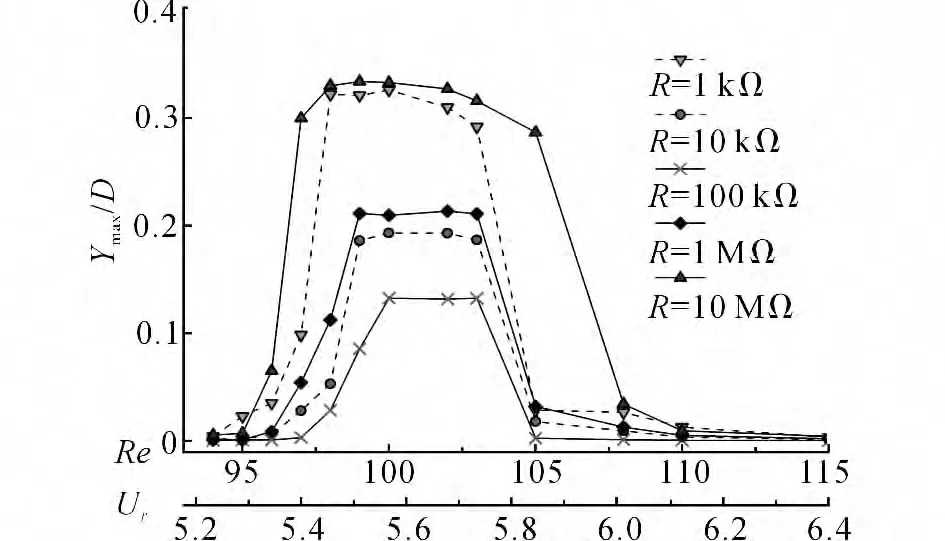
图6 圆柱涡激振动在不同载荷和雷诺数下的振幅幅值变化Fig.6 Changes of amplitude of the vortex-induced vibration under different load resistances and Reynolds numbers

在锁定区域方面，当R＝1kΩ 时，系统在Re＝98附近开始进入锁定区域；当R＝10kΩ 时，圆柱的锁定区域开始出现“滞后”现象，当Re＝99时，振幅曲线由上支过渡到锁定区域，原因是载荷使系统的固有频率和阻尼发生了改变；当R＝100kΩ 时，锁定区域较窄，当R＝100 左右时，系统进入锁定区域；当Re＝1MΩ 时，可以观察到与振幅曲线类似的规律，锁定区域变大，当Re＝98 时，系统进入锁定范围；当R＝10 MΩ、Re＝96时，系统开始进入锁定范围.综上所述，振幅曲线的锁定范围会在较大和较小载荷值下变得较宽，并经过先减小后增大的过程.

4.3 电压输出变化特性

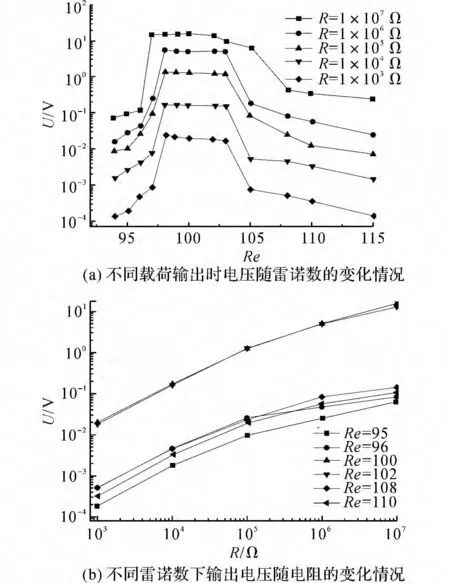
图7 圆柱涡激振动系统的输出电压变化情况Fig.7 Changes of voltage output of vortex-induced vibrating cylind

图7（a）表示不同载荷下系统电压输出的均方根值（即有效值）对Re 的变化趋势.随着载荷值的增加，系统的输出电压逐渐增大，当R＝10 MΩ，Re＝96时出现最大值.当Re增大时，电压值在锁定区域上基本保持稳定.随着载荷值的增大，电压曲线的锁振区域渐渐增大并覆盖到更高雷诺数.如当R＝1kΩ时，在Re＝98附近才开始进入锁定区域，并在Re＝103附近退出锁定区域；而当R＝10 MΩ时，在Re＝96时已经进入锁定状态，在Re＝105左右时退出锁定区域.此外，从电压有效值曲线中可以得出，下支的电压值要稍高于上支的电压值.图7（b）表示不同雷诺数下系统输出电压的有效值随着载荷的变化规律.为便于分析讨论，每个载荷分别列出3个分支下的2个雷诺数工况.从图7（b）可以看出，上支与下支的电压输出大致相近，且具有相似的变化规律.在所有的载荷下，电压输出的最大值都处于同步性区域中，增大系统载荷可以提升系统的电压输出.当R＞100kΩ 时，电压的增长幅度开始降低.当98＜Re＜103时，系统具有较高的输出电压.

4.4 功率输出变化特性

求得系统的输出电压后，以电压计算结果为基础，使用式（14）对功率进行计算［23］：

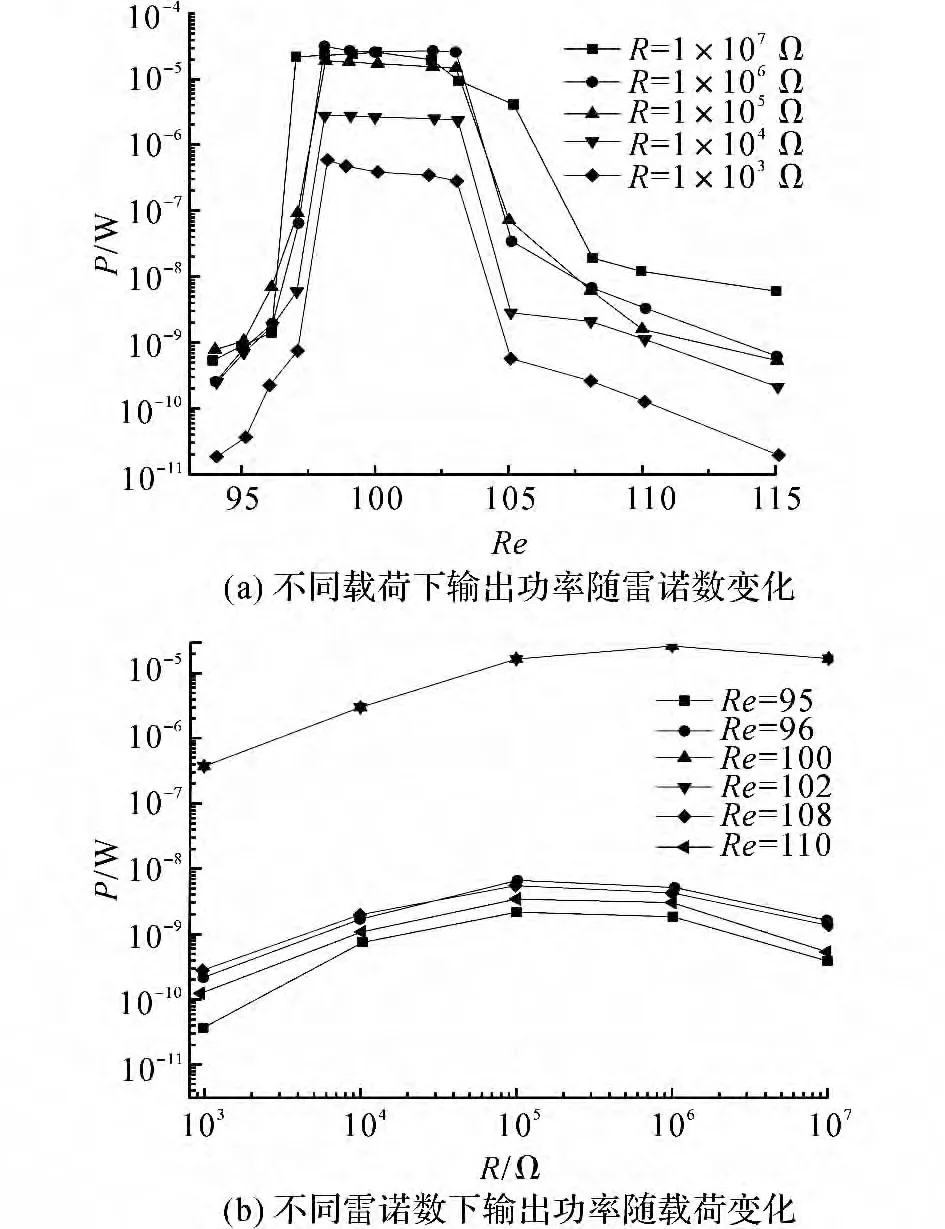
图8 圆柱涡激振动系统的输出功率变化情况Fig.8 Changes of power output of vortex-induced vibrating system

图8（a）表示不同载荷下系统功率输出P 对Re的变化曲线.功率输出的最大值出现在锁定区域内，但是与输出电压曲线不同的是，功率输出会随着载荷值的增大先增大后减小，从图8（b）可以更好地观察到这一点.图8（b）表示不同雷诺数下输出功率对不同载荷的变化曲线.当R 从1kΩ 增加到100kΩ时，功率逐渐增大，而且当R＝1 MΩ 时存在最大值.当R＝1 MΩ 时，由于分流阻尼效应此时系统的阻尼较大，振动振幅较小，说明当最大振幅出现时，并没有出现最大功率，即系统功率输出与振动振幅并不成正比关系.但是当98＜Re＜103 时，系统具有较高的功率输出，涡激振动能量转换效率较高.此项结论与文献［12］、［15］中未考虑三相耦合的计算结果不同.

5 结 论

本研究从解决涡激振动能量转换中的三相耦合问题出发，采用数值研究方法获得了系统的阻尼与固有频率随外界载荷的变化规律，导出系统电压输出的准稳态解析式，以及涡激振动能量转换系统中振动振幅、电压和功率随不同外界载荷的变化规律.主要结论如下：

（1）当外界载荷增大时，系统阻尼先增大后减小，固有频率基本不变.

（2）振动最大值和振幅曲线的锁振区域会随着载荷值的增加先减小后增大.

（3）电压输出有效值随载荷的增大而增大，同时，当载荷增大时，电压曲线的锁振区域会相应增大，并覆盖到更高的雷诺数范围.

（4）系统输出功率随着载荷的增大先增大后减小，最大输出功率并不在最大振动振幅处出现.当98＜Re＜103时，系统具有较高的功率输出，可以实现较高的涡激振动能量转换效率.

（

）：

［1］GAO X，SHIH W H，SHIH W Y.Flow energy harvesting using piezoelectric cantilevers with cylindrical extension［J］.，IEEE Transactions on Industrial Electronics，2013，60（3）：1116-1118.

［2］XU B，CHEN X.Liquid flow-induced energy harvesting in carbon nanotubes：a molecular dynamics study［J］.Physical Chemistry Chemical Physics，2012，15（4）：1164-1168.

［3］LIU H，TAY C J，QUAN C，et al.Piezoelectric MEMS energy harvester for low-frequency vibrations with wideband operation range and steadily increased output power［J］.Journal of Microelectromechanical Systems，2011，20（5）：1131-1142.

［4］ALLEN J J，SMITS A J.Energy harvesting eel［J］.Journal of Fluids and Structures，2001，15（3）：629-640.

［5］TAYLOR G W，BURNS J R，KAMMANN S M，et al.The energy harvesting eel：a small subsurface ocean／river power generator［J］.IEEE Journal of Oceanic Engineering，2001，26（4）：539-547.

［6］KWON，S D.A T-shaped piezoelectric cantilever for fluid energy harvesting［J］.Applied Physics Letters，2010，97（16）：164102（1-3）.

［7］MEHMOOD A，ABDELKEFI A，HAJJ M R，et al.Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder［J］.Journal of Sound and Vibration，2013，332（19）：4656-4667.

［8］ZHU M L，LEIGHTON G.Dimensional reduction study of piezoelectric ceramics constitutive equations from 3-D to 2-D and 1-D ［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2008，55（11）：2377-2383.

［9］丁文镜.自激振动［M］.北京：清华大学出版社，2009.

［10］ANAGNOSTOPOULOS P，BEARMAN P.Response characteristics of a vortex-excited cylinder at low reynolds numbers［J］.Journal of Fluids and Structures，1992，6（1）：39-50.

［11］BERNITSAS M M，RAGHAVAN K，BEN-SIMON Y，et al.VIVACE （vortex induced vibration aquatic clean energy）：a new concept in generation of clean and renewable energy from fluid flow［J］.Journal of Offshore Mechanics and Arctic Engineering，2008，130（4）：041101.

［12］RAGHAVAN K，BERNITSAS M M.Experimental investigation of reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports［J］.Ocean Engineering，2011，38（5）：719-731.

［13］WU W，BERNITSAS M M，MAKI K.RANS simulation vs.experiments offlowinduced motion of circular cylinder with passive turbulence control at 35，000≤Re≤130，000［C］∥Proceedings of ASME 2011 30th International Conference on Ocean，Offshore and Arctic Engineering.Rotterdam：ASME，2011：733-744.

［14］DING L，BERNITSAS M M，KIM E S.2-D URANS vs.experiments of flow induced motions of two circular cylinders in tandem with passive turbulence control for 30，000≤Re≤105，000［J］.Ocean Engineering，2013，72：429-440.

［15］MOLINO-MINERO-RE E，CARBONELL-VENTURA M，FISAC-FUENTES C，et al.Piezoelectric energy harvesting from induced vortex in water flow［C］∥Proceedings of Instrumentation and Measurement Technology Conference（I2MTC）.Graz：IEEE，2012：624-627.

［16］丁林，张力，杨仲卿.高雷诺数时分隔板对圆柱涡致振动的影响［J］.机械工程学报，2013，49（14）：133-139.DING Lin，ZHANG Li，YANG Zhong-qing.Effect of splitter plate on vortex-induced vibration of circular cylinder at high reynolds number［J］.Chinese Journal of Mechanical Engineering，2013，49（14）：133-139.

［17］BARRERO-GIL A，ALONSO G，SANZ-ANDRES A.Energy harvesting from transverse galloping［J］.Journal of Sound and Vibration，2010，329（14）：2873-2883.

［18］BARRERO-GIL A，SANZ-ANDRÉS A，ALONSO G.Hysteresis in transverse galloping：the role of the inflection points［J］.Journal of Fluids and Structures，2009，25（6）：1007-1020.

［19］MORSE T L，WILLIAMSON C H K.Steady，unsteady and transient vortex-induced vibration predicted using controlled motion data［J］.Journal of Fluid Mechanics，2010，649：429-451.

［20］YANG J，PREIDIKMAN S，BALARAS E.A strongly coupled，embedded-boundary method for fluid-structure interactions of elastically mounted rigid bodies［J］.Journal of Fluids and Structures，2008，24（2）：167-182.

［21］SCHULZ K W，KALLINDERIS Y.Unsteady flow structure interaction for incompressible flows using deformable hybrid grids［J］.Journal of Computational Physics，1998，143（2）：569-597.

［22］李宁，程礼.压电分流阻尼的虚拟实现［J］.空军工程大学学报：自然科学版，2008，9（4）：59-63.LI Ning，CHENG Li.Virtual implemention method of piezoelectric shunt damping［J］.Journal of Air Force Engineering University：Natural Science Edition，2008，9（4）：59-63.

［23］AKAYDIN H D，ELVIN N，ANDREOPOULOS Y.Energy harvesting from highly unsteady fluid flows using piezoelectric materials［J］.Journal of Intelligent Material Systems and Structures，2010，21（13）：1263-1278.