复合材料板簧刚度的预测及匹配设计方法
2015-07-11史文库李国民
柯 俊,史文库,钱 琛,李国民,袁 可
(1.吉林大学 汽车仿真与控制国家重点实验室,吉林 长春130022;2.宁波华翔汽车零部件研发有限公司,浙江 宁波3150332;3.南京依维柯汽车有限公司,江苏 南京210028)
为了满足可持续发展的要求,轻量化已经成为汽车发展的必然趋势.在刚度相同的前提下,复合材料板簧的质量不到钢板弹簧的一半,有利于降低汽车的油耗和排放.同时,它的疲劳寿命至少是钢板弹簧的2倍,对汽车的舒适性、安全性都有明显的提升作用,具有良好的应用前景.因此,复合材料板簧成为了国内外学者竞相研究的热点领域[1-3].目前,相关的研究主要集中在复合材料板簧的结构优化和接头设计方面[4-5],未见系统深入的与复合材料板簧性能匹配设计相关的研究.
复合材料板簧的刚度直接影响汽车的操纵稳定性和平顺性,是复合材料板簧的关键性能参数.然而,复合材料具有各向异性,铺层数量有几十层,设计变量非常多,导致复合材料板簧的刚度预测和匹配设计变得非常复杂和棘手.若刚度达不到要求,往往需要更改模具的结构,并反复调试铺层方案和工艺参数,导致研发成本和周期急剧上升.因此,如何准确预测复合材料板簧的刚度,并在掌握铺层参数与复合材料板簧刚度之间关系的基础上,合理高效地设计复合材料板簧的铺层方案,使之一次性地达到设计的刚度,这对复合材料板簧的推广应用具有重要意义.
本文以设计刚度为目标,匹配设计了复合材料板簧的铺层方案,并综合应用MATLAB 刚度计算程序和有限元法预测了复合材料板簧的刚度.样件的台架试验结果表明,复合材料板簧的刚度得到了准确的预测和合理的匹配设计.
1 结构设计及选材
1.1 钢板弹簧的结构和性能参数
钢板弹簧的结构和安装状态如图1所示.其中,椭圆形标记和矩形标记内分别是钢板弹簧的中部结构和接头结构.钢板弹簧的相关参数如表1所示.其中K 为刚度,H0为自由弧高,L 为长度,b为宽度,Fs为静载荷,Fm为动载荷.
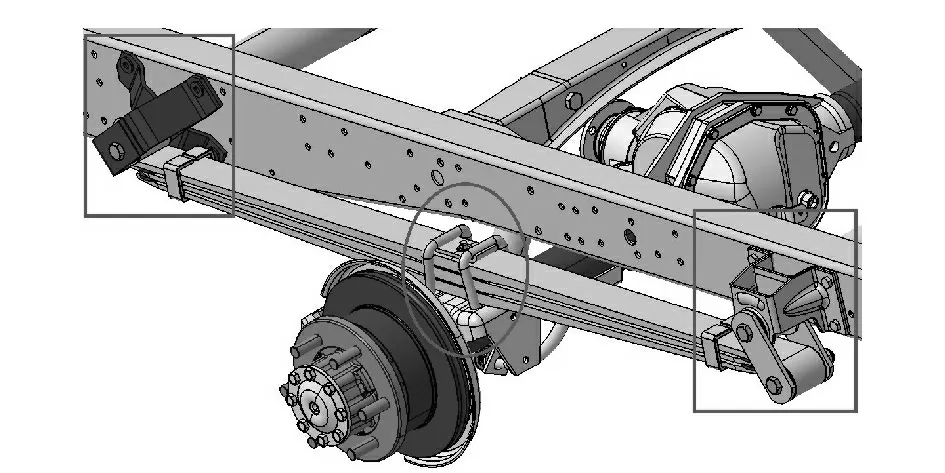
图1 钢板弹簧的结构和安装状态Fig.1 Structure and install state of steel leaf spring

表1 钢板弹簧的相关参数Tab.1 Parameters of steel leaf spring
1.2 复合材料板簧的结构设计
设计的复合材料板簧总成结构如图2所示.根据相关文献,复合材料板簧簧身的最优结构是宽度以双曲线形式变化,同时厚度从接头到中部以线性形式增加[6-7].然而,变宽度结构将导致玻璃纤维布裁剪过程中的浪费.综合考虑成本及轻量化性能,将复合材料板簧的簧身结构设计成具有较高材料利用率的等宽抛物线板簧结构.由于复合材料的比强度和比模量高于弹簧钢,当复合材料板簧和钢板弹簧具有相同的刚度时,复合材料板簧的厚度必然小于钢板弹簧.这将导致车身高度的降低并影响整车性能.因此在板簧中部下方设计了一个金属夹板.该金属夹板具有与簧身和板簧底座配对的凹凸面和凸台,从而实现了板簧总成的准确定位和纵向载荷的可靠传递,同时补足车身高度.接头结构方面,金属接头与簧身通过螺栓进行机械连接,并在簧身与金属接头之间的接触面上采用高强度粘接剂进行粘接.

图2 复合材料板簧总成Fig.2 Structure of composite leaf spring
1.3 制造材料的选择及材料的力学性能参数
聚氨酯的韧性、冲击强度和对玻璃纤维的浸润性都优于环氧树脂.因此,选择聚氨酯作为复合材料板簧的基体材料.同时,选用具有较高性价比的E玻璃纤维作为复合材料板簧的纤维增强材料.此外,选用综合性能优良的40Cr钢作为复合材料板簧中金属零件的制造材料.
对E玻璃纤维/聚氨酯层合板进行样件试制和力学性能试验.试验测得的E 玻璃纤维/聚氨酯层合板力学性能参数如表2所示.其中:Exx为纵向拉伸模量,Eyy为横向拉伸模量,Gxy为面内剪切模量,νxy、νxx、νyy为泊松比,ρ为密度,XT为纵向拉伸强度,XC为纵向压缩强度,YT为横向拉伸强 度,YC为横向压缩强度,Sxy为面内剪切强度.
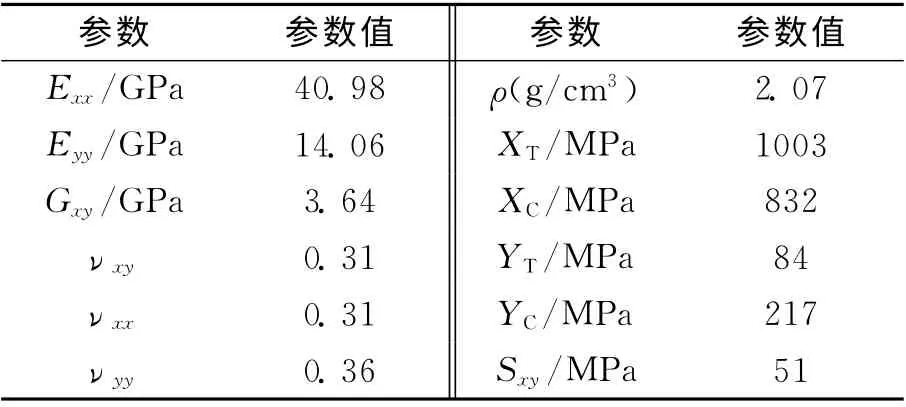
表2 E玻璃纤维/聚氨酯层合板的力学性能参数Tab.2 Mechanical properties of E-glass/polyurethane
2 铺层方案的匹配设计
2.1 铺层方案的初步设计
铺层方向为0°时,玻璃纤维高强度、高模量的优势能够得到最充分的发挥[8-10],因此选择0°作为复合材料板簧的铺层方向.由于复合材料板簧是较厚的层合板结构,对外部载荷的响应呈现一定的整体性.因此,利用传统的抛物线板簧设计理论来对复合材料板簧的簧身尺寸进行初步设计,并为铺层方案的设计提供基本的框架.
压平状态下抛物线板簧的尺寸参数如图3 所示.根据钢板弹簧的图纸,可直接确定的尺寸参数如表3所示,其中各尺寸参数的含义见图3.为了使抛物线板簧具有预期的刚度,其中部厚度(H),端部厚度(h)和各截面的厚度(hx)仍需要确定.
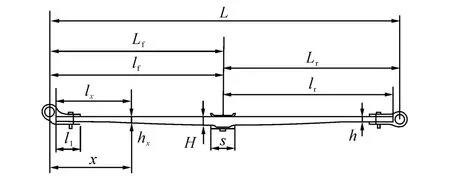
图3 压平状态下抛物线板簧的尺寸参数Fig.3 Parameters of parabolic leaf spring in flat status
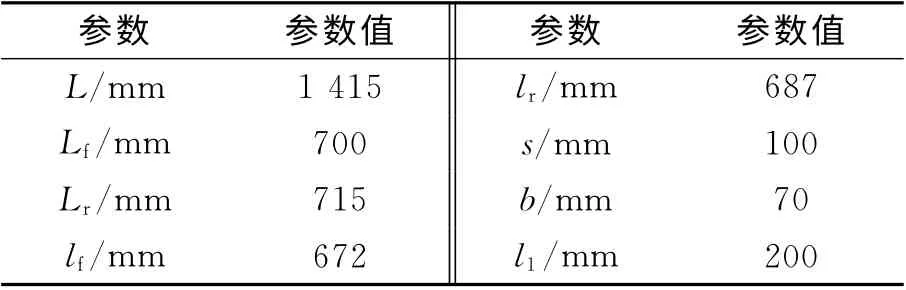
表3 复合材料板簧的已知参数Tab.3 Known parameters of composite leaf spring
若l1=200 mm,根据相关设计理论[11],前、后半段抛物线段末端的厚度分别为
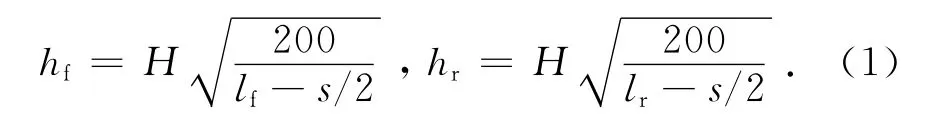
由于Lf与Lr接近,为了使板簧前、后半段的h相同,可以认为
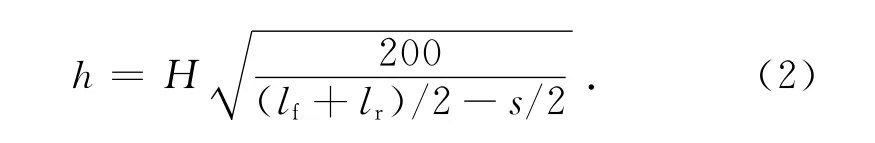
抛物线板簧的前半段的刚度(Kf)、后半段的刚度(Kr)和抛物线板簧的整体刚度(K)分别为
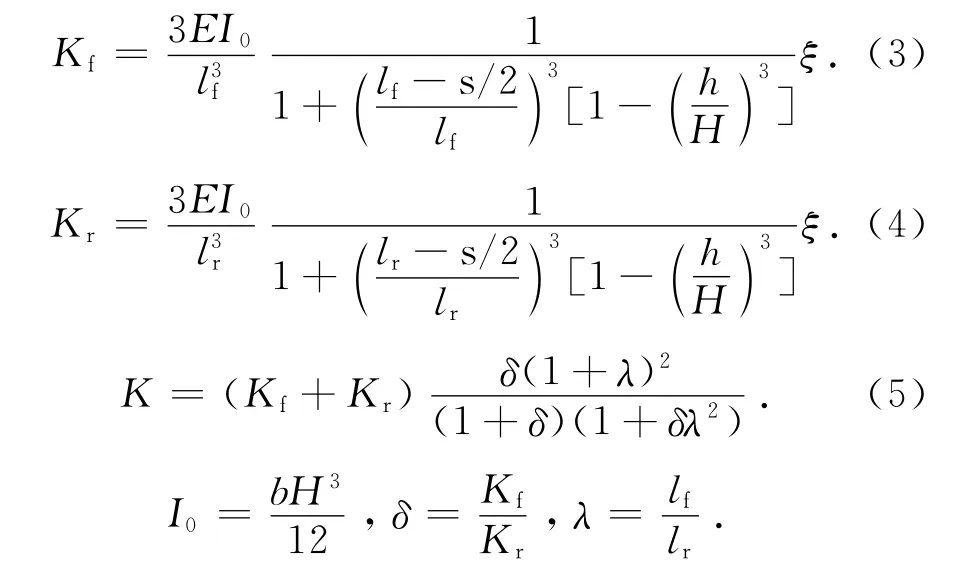
式中:E 为材料的弹性模量,ξ为修正系数,ξ=0.92,I0为截面惯性矩,δ和λ均为计算参数,无物理意义.
将K =120N/mm 代入式(5),联立式(2)、(3)、(4),解得H≈37mm,h≈21mm,因此分别选定37和21mm 作为复合材料板簧的中部厚度和末端厚度.
钢板弹簧的自由弧高H0=140 mm,因此复合材料板簧自由状态下的曲率半径为
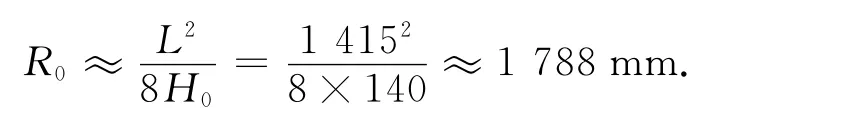
通过上述计算,可初步确定复合材料板簧的大体尺寸.纤维体积含量为58%的单向E 玻璃纤维/聚氨酯层合板的厚度为0.808 mm,则铺层总数量为37/0.808≈46.各铺层的宽度为70mm,各铺层长度可通过抛物线板簧的抛物线段外围轮廓确定.通过上述方法即可建立起复合材料板簧的初步铺层方案.
复合材料板簧的簧身是抛物线形,因此复合材料板簧的簧身被分成4部分,如图4所示.图中,区域A 由等长铺层构成,区域B 由渐变长度铺层构成,区域C 由渐变长度的短铺层构成.为了降低区域B 和区域C 中铺层发生剥离破坏的可能性,设置区域D.区域D 由等长的长铺层构成.
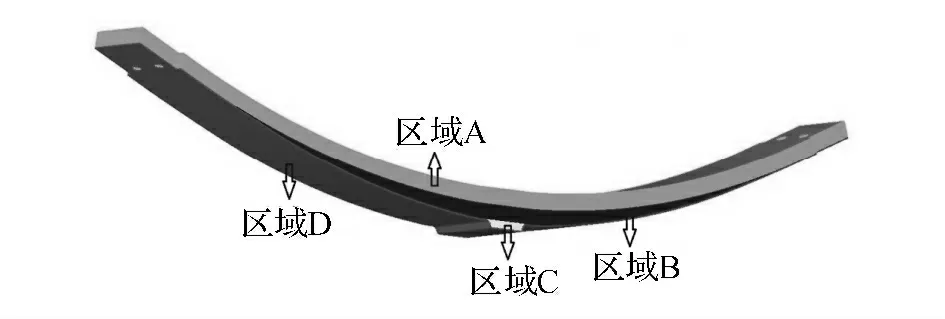
图4 初步铺层方案的区域分布Fig.4 Regions in initial layer scheme
2.2 复合材料板簧刚度的计算理论
有了具体的铺层后,就可以进行复合材料板簧刚度的理论计算了.复合材料板簧的受力分析图如图5所示.其中,F 为复合材料板簧受到的垂直外力,Ff和Fr分别为复合材料板簧前、后接头受到的支反力.ab 段和cd 段是复合材料板簧产生变形的区域.以ab 段为例,将ab 段平均分成许多薄片,每片长度为Δx,每片的弯曲刚度用Ki表示,其中i是每个薄片的序号.
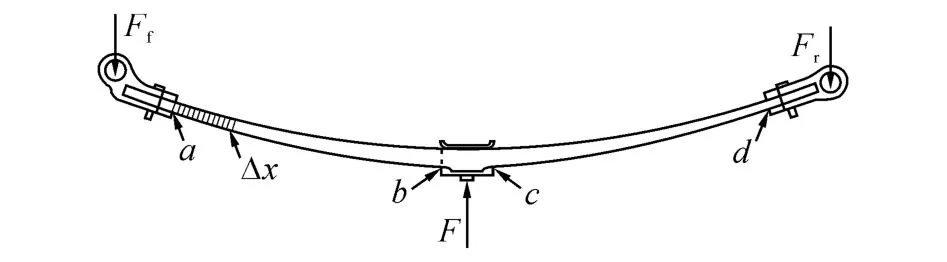
图5 复合材料板簧的受力分析图Fig.5 Force diagram of composite leaf spring
对第i个薄片,选择复合材料板簧的圆周方向作为x 轴,宽度方向为y 轴,厚度方向为z 轴.由于复合材料板簧具有一定的曲率,且是变截面的,因此第i个薄片的中性轴与几何中心轴不重合,因此引入中性轴位移系数δ 来实现计算过程中误差的修正,且有

式中:di为第i个薄片的中性轴(拉应力与压应力的分界)与几何中心轴之间的距离.hi为第i 个薄片的厚度.若在第i个薄片中,第k层铺层的截面与薄片的几何中心轴之间距离为zikg,则第k 层铺层的截面与薄片的中性轴之间距离为
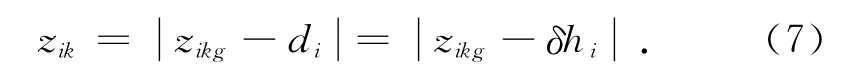
对具体的铺层而言,zikg和δhi均为已知量,则zik可通过式(7)计算得到.
根据经典层合板理论[12],对第i个薄片,其正则化刚度系数由下式计算得到

式中:


式中:n为第i个薄片的铺层数量,θk为第i个薄片中第k个铺层的铺层角度.
第i个薄片的正则化弯曲刚度矩阵D*,正则化面内刚度矩阵A*和正则化耦合刚度矩阵B*可通过上面的正则化刚度系数表达式得到.则第i个薄片的弯曲刚度矩阵D,面内刚度矩阵A 和耦合刚度矩阵B 分别为
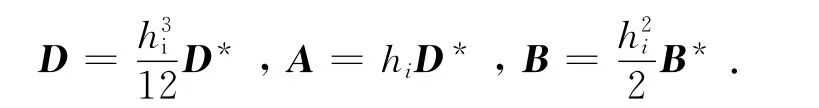
可构造出第i个薄片的柔度矩阵为
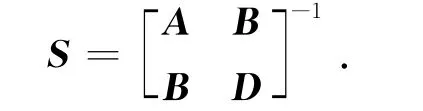
对第i个薄片,其承受的载荷向量可表示为
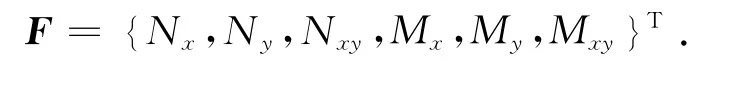
式中:Nx、Ny、Nxy为第i个薄片承受的力分量,Mx、My、Mxy为第i个薄片承受的扭矩分量.
则第i个薄片的应变向量可表示为
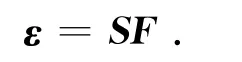
应变向量的第4行可表示为εx,该应变分量是由Mx引起的,因此第i个薄片的弯曲刚度为
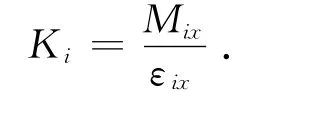
根据材料力学,由Ff和Fr引起的板簧挠度分别为
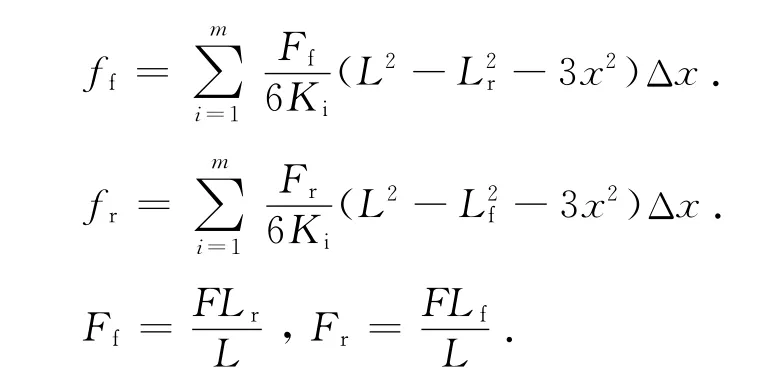
式中:m 为ab段或cd 段中薄片的数量.则复合材料板簧的前半段刚度和后半段刚度分别为
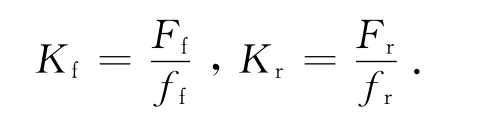
则复合材料板簧的刚度为
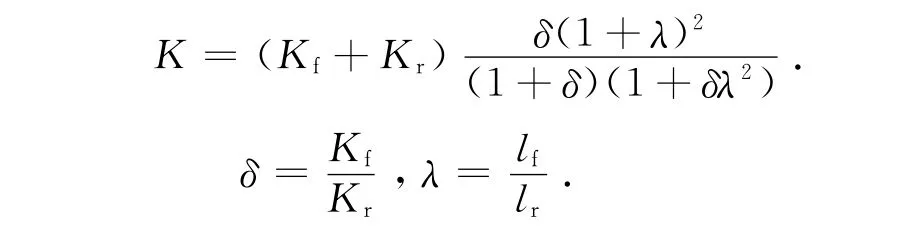
2.3 铺层方案关键参数的刚度灵敏度分析
基于各向同性材料的传统抛物线板簧刚度计算结果和基于各向异性材料的复合材料板簧刚度计算结果的误差是必然存在的,因此需要对初步铺层方案进行调整,以修正复合材料板簧的刚度.因此,如何高效合理地修正复合材料板簧的刚度,是复合材料板簧刚度匹配设计中的重要问题.
在MATLAB软件中,根据2.2 节中的计算理论,编写了复合材料板簧的刚度计算程序,并利用该程序计算了铺层方案关键参数与复合材料板簧刚度之间的关系,如图6 所示.其中,θ 为铺层角度,φB为纤维体积分数,nA为区域A 中的铺层数量.
根据图6(a),θ与K 之间的关系是非线性的,0°铺层对应的刚度最高而40°~60°铺层对应的刚度最低.同时,φB 与K 之间的关系是线性的,K 随φB的升高而增大.与φB 相比,K 随θ 的变化斜率更大,因此θ的刚度灵敏度大于φB 的刚度灵敏度.根据图6(b),nA与K 的关系是非线性的,且随着铺层数量的增多,K 的增大幅度有增加的趋势,且nA的刚度灵敏度大于φB 的刚度灵敏度.根据图6(c),当铺层角度为0°时,K 随nA的增多而增大的速率最快,且nA的刚度灵敏度大于θ的刚度灵敏度.
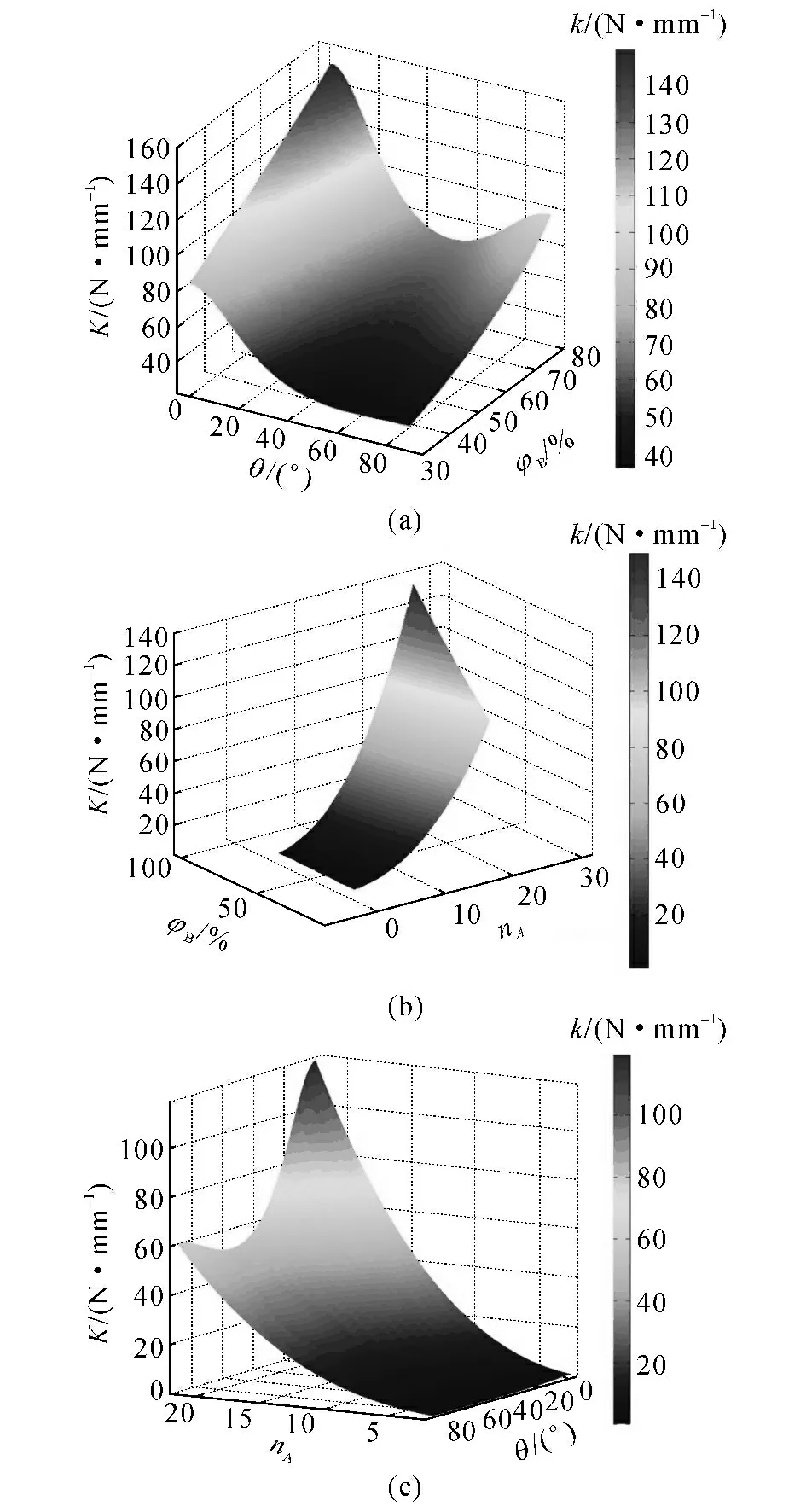
图6 铺层关键参数与复合材料板簧刚度之间的关系Fig.6 Relationships among key parameters of layer scheme and stiffness of composite leaf spring
综上所述,通过调整铺层角度、纤维体积分数与区域A 中的铺层数量均可达到调整复合材料板簧刚度的目的,但灵敏度不同.3个关键参数对复合材料板簧刚度的灵敏度从高到低排列分别是nA,θ及φB.同时,增减区域A 中的铺层数量既不改变模具结构和复合材料板簧的应力分布状态,具有很强的可行性,因此采用增减区域A 中的铺层数量的方法来修正复合材料板簧初步铺层方案的刚度.
2.4 复合材料板簧刚度匹配设计的计算程序
根据上述设计理论,采用MATLAB 软件编写了复合材料板簧的刚度匹配计算程序,程序的流程图如图7所示.
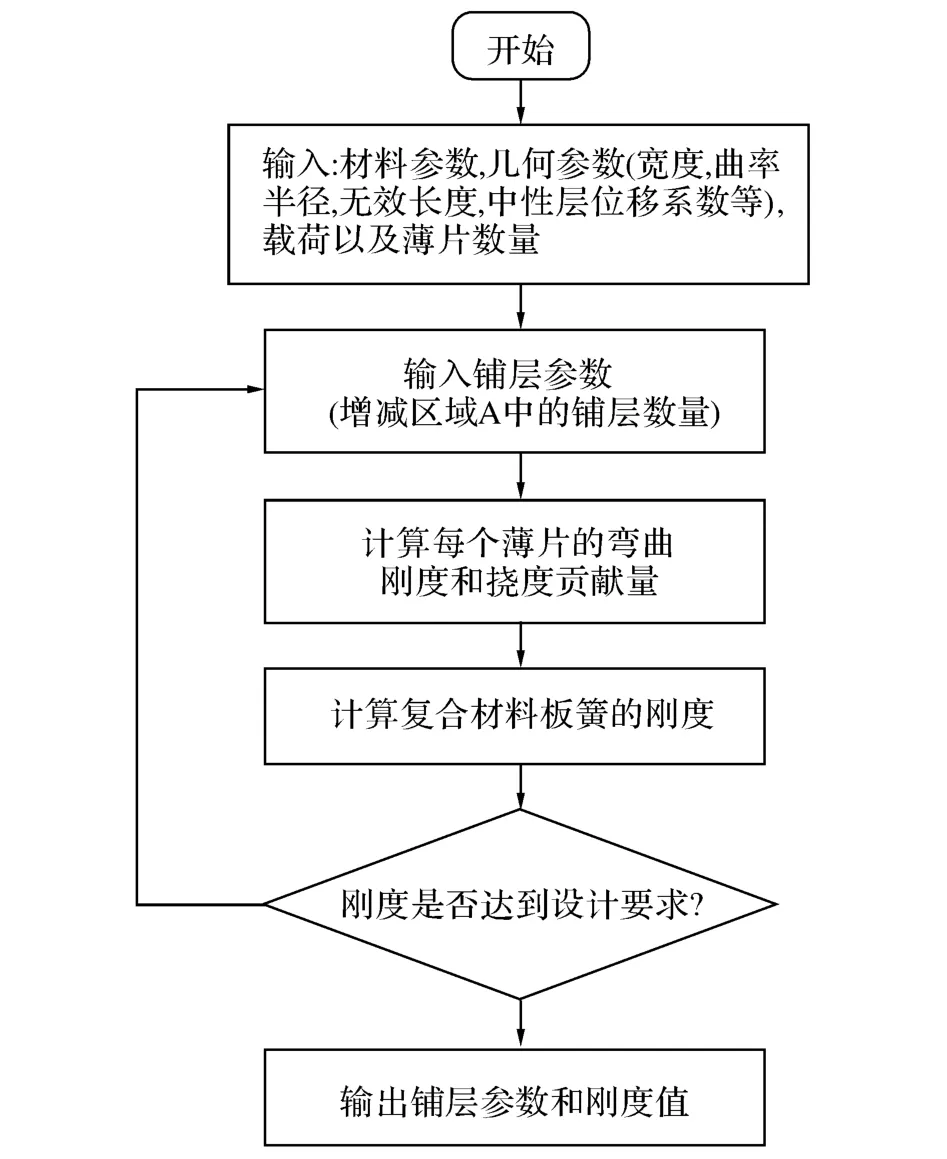
图7 计算程序的流程图Fig.7 Flow-chart of MATLAB program
2.5 铺层方案的确定
由于0°铺层具有最佳的强度和抗蠕变、抗疲劳性能,因此将复合材料板簧的铺层角度全部设置为0°(纤维排布方向沿板簧圆周方向).为了保证复合材料板簧的接头强度,簧身末端钻孔处设置一定比例的45°铺层.根据刚度匹配计算程序的计算结果,若将复合材料板簧的刚度设计为120N/mm,区域A、B、C 和D 中的铺层数量分别为:22层,21层,10层和2层.其中,区域C 中的铺层数量对复合材料板簧的刚度影响较小,其铺层数量由簧身凸台的尺寸决定.
3 复合材料板簧刚度的有限元分析
虽然MATLAB 计算程序可以快速地预测复合材料板簧的刚度,但理论计算模型经过了大量的简化,且不能直观地验证复合材料板簧的应力分布和变形状态.为了弥补MATLAB 计算程序的不足,通过有限元方法来进一步验证铺层设计方案的合理性.
3.1 有限元模型的建立[13-15]
复合材料板簧的三维几何模型是在CATIA 软件中建立的.利用CATIA 软件切割出簧身的4 个铺层区域,并对复合材料板簧各零件进行模拟装配和干涉分析.将复合材料板簧的三维几何模型导入HYPERMESH 软件中进行网格划分.由于铺层间的横向剪切效应和铺层截面的正应力不能忽略,因此采用体单元对复合材料板簧进行离散化.单元类型采用C3D8I单元,因为该类单元可以避免剪切自锁现象,且单元具有较小变形的情况下对位移和应力的计算精度较高.为了保证网格质量,采用六面体网格进行网格化分.最终为每一铺层建立一层单元,并使相邻铺层单元之间的节点重合.模型共有457 482个单元和518 750个节点,如图8所示.

图8 复合材料板簧的网格Fig.8 Gridding of composite leaf spring
在删除几何元素后,将复合材料板簧的网格模型以INP 文件形式导入 ABAQUS 软件.在ABAQUS软件中,E 玻璃纤维/聚氨酯层合板的材料参数在Property模块中以工程常数的方式定义,参数值按表1 输入.复合材料板簧的铺层参数由composite layup manager对话框定义,其中铺层方向按照discrete method定义.然后,在Step模块中建立3个载荷步,分别模拟中部U 型螺栓夹紧过程(0.02s),预加载过程(0.02s)和施加正弦垂向载荷过程(0.03s).在Step模块中要求输出参考点A 的载荷-时间曲线和位移-时间曲线.参考点A 与复合材料板簧的中部耦合.此外,在Interaction模块定义绑定约束和耦合约束,在Load模块定义载荷和边界条件.其中,载荷施加在参考点A 上,载荷幅值与钢板弹簧图纸标明的动载荷相同;接头的运动约束通过约束参考点B 和参考点C 的自由度来实现.参考点B 和参考点C 分别与复合材料板簧的后接头内表面和前接头内表面耦合.建立的复合材料板簧有限元模型如图9所示.
3.2 有限元模拟结果
将模型提交ABAQUS 软件的求解器进行计算,并通过后处理模块对计算结果进行处理.由参考点A 输出的复合材料板簧刚度曲线如图10 所示.其中S 为参考点A 的位移,F 为参考点A 受到载荷,根据图10,通过有限元仿真预测的复合材料板簧刚度为119.8N/mm,满足设计目标.
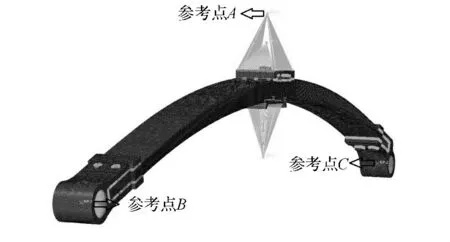
图9 复合材料板簧的有限元模型Fig.9 Finite element model of composite leaf spring
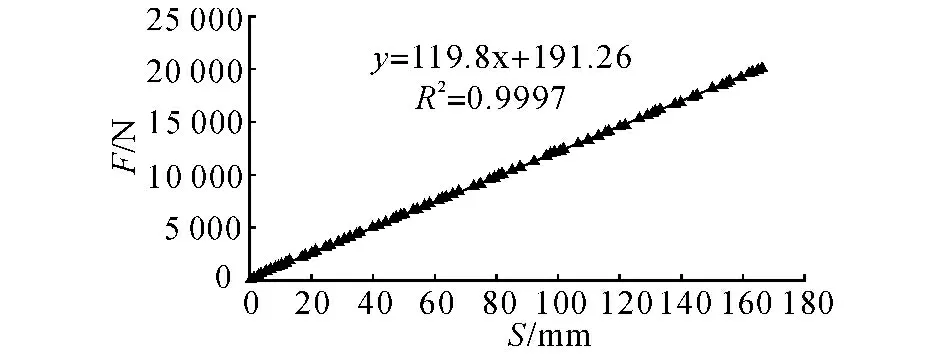
图10 通过有限元仿真得到的复合材料板簧刚度曲线Fig.10 Predicted stiffness curve of composite leaf spring according to finite element method
复合材料板簧承受18 500N 的最大垂向载荷时的应力云图如图11所示.从图11可看出,复合材料板簧的最大拉应力是487.6 MPa,最大压应力为104.9MPa,均远低于E 玻璃纤维/聚氨酯层合板的拉伸极限强度和压缩极限强度.此外,簧身的应力分布比较均匀,没有明显的应力集中现象,是近似的等强度梁,说明复合材料板簧的设计方案是合理的,可以进行样件试制.

图11 复合材料板簧的应力云图Fig.11 Stress nephogram of composite leaf spring
4 验证试验
为了验证复合材料板簧刚度预测及匹配设计方法的正确性,通过高压RTM 工艺(高压树脂传递模塑成型工艺)制作了3 个复合材料板簧样件,如图12所示.复合材料板簧总成的重量不到钢板弹簧总成重量的40%.样件试制的工艺参数为:抽真空后的模具温度为70 ℃左右,树脂注射压力为11 MPa左右,合模压力为200t,保压30min.后固化温度为120 ℃,后固化时间为2h.

图12 复合材料板簧的样件Fig.12 Samples of composite leaf spring
复合材料板簧的刚度台架试验如图13所示.根据试验结果,3个复合材料板簧样件的平均刚度为118 N/mm,因此复合材料板簧的试验刚度为118N/mm.

图13 复合材料板簧的刚度台架试验Fig.13 Bench test for stiffness of composite leaf spring
复合材料板簧刚度的设计值、预测值和试验值之间的对比如表4所示.从表4可看出,3个刚度值的误差小于2%,说明复合材料板簧的刚度得到了准确的预测和正确的匹配设计.
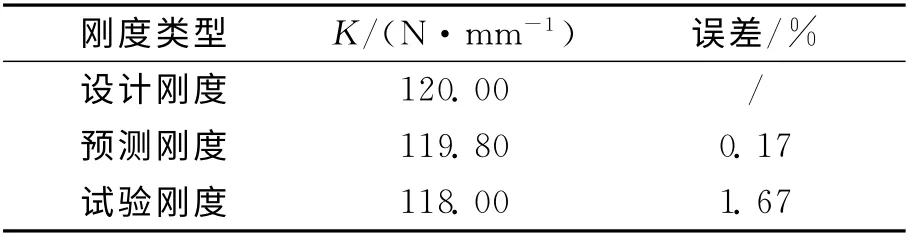
表4 刚度设计值、预测值及试验值之间的对比Tab.4 Comparison among expected stiffness,predicted stiffness and test stiffness
5 结 论
(1)综合应用MATLAB计算程序和有限元法,可以快速可靠地预测复合材料板簧的刚度,并直观地展示复合材料板簧的应力分布和变形状态.
(2)根据有限元模拟的结果,设计的复合材料板簧近似为等强度梁,具有较高的材料利用率.
(3)根据样件的台架试验结果,复合材料板簧的刚度得到了准确的预测和正确的匹配设计.说明提出的复合材料板簧刚度的预测及匹配设计方法是正确的和有效的,可为类似工程问题提供参考,并大幅度降低复合材料板簧的开发周期和成本.
(
):
[1]AL-QURESHI H A.Automobile leaf springs from composite materials [J].Journal of Materials Processing Technology,2001,118(1/3):58-61.
[2]MAHDI E,ALKOLES O M S,HAMOUDA A M S,et al.Light composite elliptic springs for vehicle suspension[J].Composite Structures,2006,75(1/4):24-28.
[3]HOU J P,CHERRUAULT J Y,JERONIMIDIS G,et al.Design,testing and simulation of fiber composite leaf springs for heavy axle load[J].Journal of Strain Analysis for Engineering Design,2005,40(6):497-504.
[4]SANCAKTAR E,GRATTON M.Design,analysis,and optimization of composite leaf springs for light vehicle applications[J].Composite Structures,1999,44(2/3):195-204.
[5]SUBRAMANIAN C,SENTHILVELAN S.Joint Performa-nce of the glass fiber reinforced polypropylene leaf spring[J].Composite Structures,2011,93(2):759-766.
[6]SHOKRIEH M M,REZAEI D.Analysis and optimization of a composite leaf spring [J].Composite Structures,2003,60(3):317-325.
[7]RAJENDRAN I,VIJAYARANGAN S.Optimal design of a composite leaf spring using genetic algorithms[J].Computers and Structures,2001,79(11):1121-1129.
[8]FERREIRA J A M,COSTA J D M,REIS P N B,et al.Analysis of fatigue and damage in glass-fibre-reinforced polypropylene composite materials[J].Composites Science and Technology,1999,59(10):1461-1467.
[9]FERREIRA J A M,COSTA J D M,REIS P N B.Static and fatigue behavior of glass-fibre-reinforced polypropylene composites[J].Theoretical and Applied Fracture Me-chanics,1999,31(1):67-74.
[10]KUMAR M S,VIJAYARANGAN S.Analytical and experimental studies on fatigue life prediction of steel and composites multi-leaf spring for light passenger vehicles using life data analysis[J].Materials Science-Medziagotyra,2007,13(2):141-146.
[11]王望予.汽车设计[M].北京:机械工业出版社,2004:189-190.
[12]王耀先.复合材料力学与结构设计[M].上海:华东理工大学出版社,2012:52-103.
[13]KUEH J-T J,FARIS T.Finite element analysis on the static and fatigue characteristics of composite multileaf spring [J].Journal of Zhejiang University:SCIENCE A,2012,13(3):159-164.
[14]SUBRAMANIAN C,SENTHILVELAN S.Shortterm flexural creep behavior and model analysis of a glass-fiber-reinforced thermoplastic composite leaf spring[J].Journal of Applied Polymer Science,2011,120(6):3679-3686.
[15]常崇义,刘书田,王成国.单向纤维复合材料粘弹性性能预测[J].计算力学学报,2006,23(4):414-418.CHANG Chong-yi,LIU Shu-tian,WANG Cheng-guo.Prediction of visco-elastic property of unidirectional fiber reinforced composite materials[J].Jisuan Lixue Xuebao/Chinese Journal of Computational Mechanics,2006,23(4):414-418.
