Hansbo类有限单元法的非连续分片试验

凌道盛，石吉森，张如如，王云岗

（1.浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州310058；2.浙江大学 岩土工程研究所，浙江 杭州310058；3.浙江大学 城市学院，浙江 杭州310015）

裂纹（剪切带）等非连续变形在土木工程、机械工程、航空航天等工程领域结构破坏过程中普遍存在，非连续变形分析已成为相关工程领域的研究热点之一.由于非连续变形的产生与扩展是一个路径事先未知的动态过程，将裂纹限制在单元边界的常规有限单元法存在明显的局限性［1-2］，能够表征单元内部非连续变形的新型分析方法得到越来越多的关注.

为克服常规有限元法的困难，石根华［3］最早（1991年）基于单位分解（Partition of unity）和数值流形的思想，提出了适用于非连续变形分析的数值流形法［4-6］，虽然单位分解法的概念直到1997年才被Babuška等［7］正式提出.同样基于单位分解思想，Belytschko等［8-9］通过引入Heaviside函数和裂尖函数描述裂纹变形的非连续性和裂尖应力的奇异性，提 出 了 扩 展 有 限 元 法（extended finite element method）［10-11］.Hansbo等［12-13］提出了基于常规有限元位移插值描述单元内非连续变形的方法，被广泛称为Hansbo和Hansbo方法（Hansbo ＆ Hansbo's Method）.已经证明［14］，Hansbo和Hansbo方法与未引入裂尖奇异函数的扩展有限元法是完全等价的.Song 等［15］提 出 的 虚 节 点 法（phantom node method）实质上是Hansbo和Hansbo方法的另一种形式.Ling等［16-18］提出了基于网格分离和位移映射的有限元位移插值技术及增强有限单元法（augmented finite element method）.与扩展有限元法和Hansbo等提出的方法不同，增强有限单元法将开裂后的单元视为2个完全独立的单元，使得复杂裂纹扩展模拟更加容易实现.需要指出的是，Hansbo和Hansbo方法是增强有限单元法的一个特例，也是裂纹扩展问题中最常用的一种形式.目前，所有与Hansbo和Hansbo方法本质相同的方法被统称为Hansbo和Hansbo 类方法（Hansbo ＆ Hansbo's type of methods）.

为避免体积不可压缩条件下模拟裂纹扩展时出现网格自锁，Dolbow 等［19］在扩展有限元法位移插值中引入加强假定应变（enhanced assumed strain），并设计了一个非连续分片试验（discontinuous path test）来测试其构造的单元的性能.

本文基于作者提出的增强有限单元法，利用Dolbow 等设计的非连续分片试验对Hansbo 和Hansbo类有限单元法进行测试，发现该类方法普遍不能以机器精度通过非连续分片试验，从理论上揭示了分片试验失败的原因，并提出了相应的解决方法.

1 增强有限单元法［16-18］

增强有限元法将常规有限单元分离为几何上相互独立的数学单元和物理单元，利用数学单元构造离散位移函数，利用物理单元定义真实物理区域.与数值流形法和广义有限单元法不同，增强有限单元法的关键在于引入映射法则将数学单元和物理单元的离散位移场有机关联在一起，从而极大提高了有限单元法的适用性和灵活性，如图1所示.最简单的一种映射法则是物理单元采用与数学单元完全相同的离散位移函数，即简单覆盖法则.简单覆盖法则也是数值流形法和广义有限单元法在构造物理单元（或积分网格）离散位移函数时采用的法则.为简单起见，本文也限于简单覆盖法则.

图1 增强有限单元Fig.1 Augmented finite element

利用分离的数学单元和物理单元可以实现任意强非连续变形模拟.考虑如图2（a）所示被裂纹分割的单元，为简便起见，假定裂纹穿过前数学单元和物理单元完全重合.裂纹穿过后，物理单元被分割为2个不同的物理区域，如图2（b）和（c）中阴影部分所示.为描述2个物理区域间的非连续变形，分别为每个物理区域构造数学单元，并令2个新的数学单元（图2中的1I2I3I4I和1II2II3II4II）具有和原数学单元（图2中的1234）相同的几何形状，占据相同的空间区域.为保证与邻单元间的位移连续性，数学节点1II、2II、3I、4I为原数学节点1、2、3、4，其余数学节点为新富集的数学节点.不难看出，描述非连续变形时，基于简单覆盖法则的增强有限单元法与Hans-bo和Hansbo方法本质上是相同，不同的是，Hansbo和Hansbo方法将开裂后的单元视为一个含裂纹的单元，而增强有限单元法将其当作2个完全独立的单元.

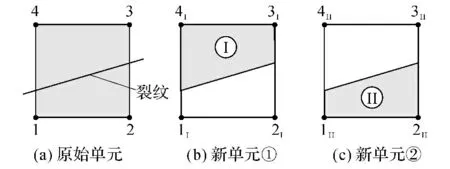
图2 非连续变形的增强有限元描述Fig.2 Simulation of discontinuous deformation in AFEM

数学单元和物理单元的分离使得物理单元可以具有任意的几何形状，为实现刚度矩阵等在单元上的数值积分，增强有限单元法［18］采用与扩展有限元法相同的求积技术，将物理区域细化为若干三角形子域，对每个子域采用Hammer积分.对于四边形或可细化为四边形的物理单元，也可采用Gauss积分.为简洁起见，本文用Q4和T3分别表示4节点四边形数学单元和3 节点三角形数学单元；用H3和H1 分别表示三角形物理子域3 点和1 点Hammer积分；用G2和G1分别表示四边形物理子域2×2和1×1点Gauss积分.于是，Q4H3代表含裂纹单元为4节点四边形数学单元，积分采用三角形物 理 子 域3 点Hammer 积 分，如 图3（a）所 示；T3G2H1则代表含裂纹单元为3节点三角形数学单元，积分混合采用G2和H1这2种方法，且G2优先，如图3（c）所示.图3（b）还给出了Q4G2示意图.

图3 网格类型和积分方法Fig.3 Different meshes and integration methods

2 非连续分片试验

Dolbow 等［19］设计的非连续分片试验如图4示，分析域Ω 为3×3的正方形区域，界面无作用力的裂纹Γ 将分析域分成2个相同的区域Ω＋和Ω-，两侧分别作用大小为2t和t MPa·m 的均布拉力.与文献［19］不同，本文不考虑材料不可压缩这种特殊情况，取材料弹性模量E＝1 000MPa，泊松比ν＝0.25.该问题满足平面应变假定，其应力精确解为

式中：σx为x 方向正应力，σy为y 向正应力，τxy为剪应力，t为常规变量，可以为任意数值.

Dolbow 等［19］利用没有富集裂尖奇异函数的扩展有限元法对该问题进行分析，采用图4 所示的3×3的网格，其中中间一行单元为含裂纹单元.本文以增强有限单元法为例，利用该算例对Hansbo和Hansbo类方法进行分片试验测试.需要指出的是，对于图4示网格，增强有限单元法采用12个单元，其中裂纹附近的6个单元的物理单元不再与对应的数学单元重合.不难看出，Ω＋和Ω-对于增强有限单元法而言是2个相互独立的分析域，可以分别进行计算.不失一般性，本文仅对Ω-进行分析.

图4 非连续分片试验Fig.4 Discontinuous patch test

为对比研究数学单元类型、刚度矩阵积分方法对分片试验结果的影响，本文以图4网格为基础，构造如图5所示的10种网格.图中粗实线代表数学网格，阴影部分代表物理区域，虚线代表物理单元的子域划分.其中，（a）和（b）采用常规四边形有限单元；（c）和（d）采用与图4相同的数学网格；（g）和（h）采用梯形数学单元，且梯形两平行边与裂纹面平行；（i）和（j）中，裂纹面所在的数学单元为平行四边形单元.

为便于评价计算精度，利用积分点应力定义相对误差指标为

式中：σ为3个应力分量中的任意一个；σexact和σh分别为应力精确值和计算值；为特征应力值，这里取为所有积分点中求最大值.10种网格计算结果如表1所示，其中试验结果以计算误差是否达到机器误差（10-15）为评价标准.

图5 分片试验网格Fig.5 Different meshes for discontinuous patch tests

表1 分片试验应力相对误差指标统计表Tab.1 Relative error indexes of stresses for different meshes

由表1可以看出，采用三角形数学单元的网格能以机器精度通过分片试验；除Q4G2-S、Q4G2-M、Q4G2-P和Q4H3-P 这4 种情况外，采用四边形数学单元的网格都不能以机器精度通过分片测试.

为进一步考察数学单元和物理单元形状对计算精度的影响，采用如图6所示的Q4G2和Q4H3网格进行测试.图6中f 为一无量纲的量，4个单元的形状随着f 的变化而改变，当f＝1时，即为图5（c）和（d）示网格.

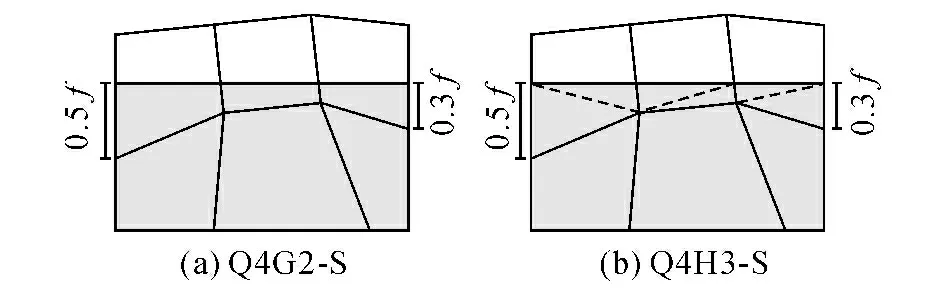
图6 网格变化示意图Fig.6 Mesh varying with f

如表2所给出了不同f 值时应力相对误差指标计算结果.由表可见，单元形状对计算误差有显著的影响.当f＝0.5时，数学和物理单元的形状相对较好，计算误差相对较小；当f＝3.0 时，应力相对误差指标分别达到7.29×10-3和2.32×10-3.

表2 网格变化时应力相对误差指标Tab.2 Relative error indexes of stresses for different fs

由表可见，应力相对误差指标接近10-2.无论从实用角度还是理论角度，这样的误差都不是可以接受的，尤其是对于裂尖附近的含裂纹单元.这为Hansbo和Hansbo类方法应用裂纹扩展分析带来不确定性.

3 分片试验失败原因

无论是三角形还是四边形数学单元，其离散位移函数能够描述区域Ω＋和Ω-内的简单拉伸变形.包括增强有限单元法在内的Hansbo和Hansbo类方法完全具备描述非连续变形的能力.由于材料非不可压缩，网格也没有出现明显畸形，可以排除整体刚度矩阵病态引起分片试验失败.因此，数学单元和物理单元的几何分离及刚度矩阵积分技术引起的刚度矩阵数值误差可能是导致分片失败的原因.

3.1 增强有限单元刚度矩阵

根据等参插值技术，4节点四边形数学单元内任意点的坐标和位移可表示为

式中：a1，a2，…，d2为与数学单元节点（数学节点）坐标有关的常数；e1，e2，…，h2为与数学单元节点位移线性相关的待求量；ξ和η 为数学单元的母单元坐标.

将ξη 项视为常数，联立式（3）和（4）可得

利用式（3）和（4），数学单元的Jacobi矩阵J 及其逆矩阵J-1可表示为

将式（9）和（10）代入几何方程，可得单元应变为

式中：

其中，

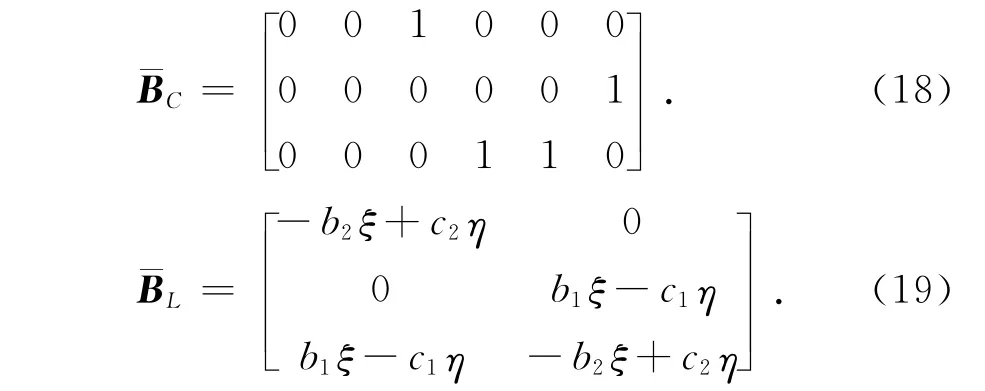
利用虚功方程导出单元的刚度矩阵为

式中：ΩPE为物理单元所占据的空间区域，D 为材料的弹性系数矩阵.

将式（17）代入式（20），可得

其中

对于3节点三角形数学单元，不难证明，只需令ξ和η 为数学单元的面积坐标，令d1，d2，h1，h2，，，和为零，上述推导仍然成立.此时，数学单元的Jacobi矩阵和Jacobi行列式与坐标无关，且有

当物理单元为4节点四边形单元时，单元内任意点的坐标可插值表示为

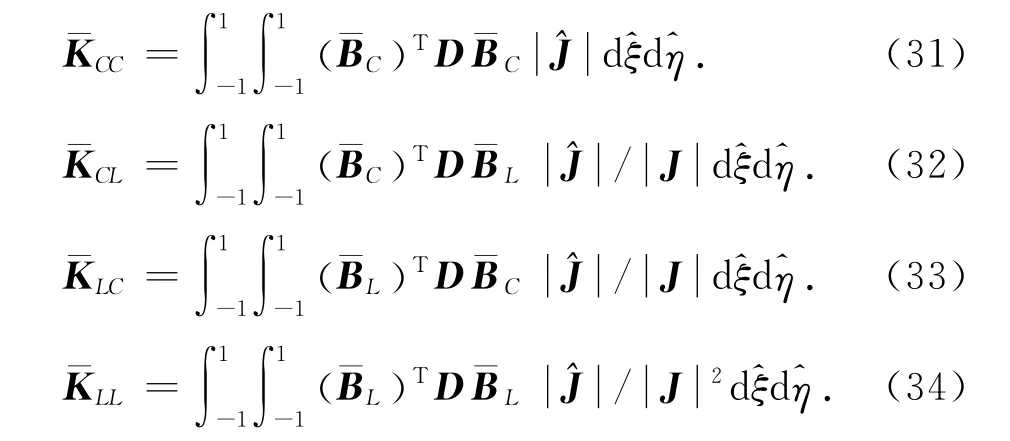
式（31）～（34）一般采用Gauss积分进行数值求积.

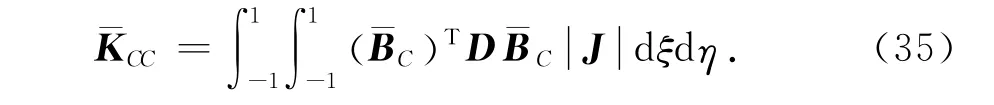
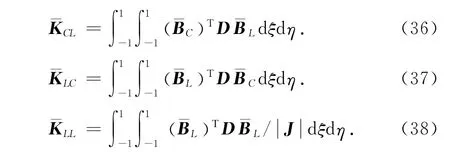
比较式（31）～（34）和式（35）～（38）可以看出，数学单元和物理单元分离使得刚度矩阵积分表达式更为复杂，表现在2个方面：

当物理单元为3节点三角形时，式（22）～（25）改写为如下形式，

3.2 刚度矩阵积分误差

为分析Hansbo和Hansbo类方法不能以机器精度通过非连续分片试验的原因，本文根据数学单元和物理单元的类型，分4种情况分析刚度矩阵的积分误差.不失一般性，假设一个单元只含一个物理子域，同时不考虑计算机的舍入误差.

1）四边形数学单元和四边形物理单元

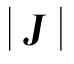
与Q4G2-M 型网格相比，Q4G2-S 型网格更为特殊，其数学单元和物理单元完全重合，此时ξ ＝、η＝，增强有限元单元退化为常规有限元单元.

2）四边形数学单元和三角形物理单元

3）三角形数学单元和三角形物理单元

4）三角形数学单元和四边形物理单元

4 数值算例

第3节从理论上证明了数学单元和物理单元分离及刚度矩阵积分技术引起单元刚度积分精度降低，是导致非连续分片试验失败的原因.本节通过三个算例从数值方面进一步验证上述推导的正确性.

算例1 如图7所示为直角梯形分析模型，包含1个常规有限单元，即物理单元与数学单元重合，几何尺寸、边界条件如图所示.在模型的右竖直边和斜边上分别施加荷载q1＝1 MPa·m，q2＝1／MPa·m，设材料的E＝1 MPa，ν＝0.1.该问题应力的理论解为σx＝1，σy＝τxy＝0.

图7 常应力直角梯形Fig.7 Right trapezoid with constant stress

表3 应力相对误差指标Tab.3 Relative error indexes of stresses

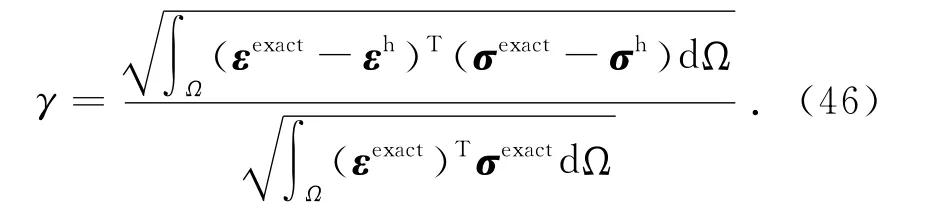
式中：σ 和ε 分别为应力矢量和应变矢量；上标exact和h分别代表精确解和数值解.

图8 常应力矩形Fig.8 Rectangle with constant stresses

如图9所示为相对误差能量范数随h的变化关系曲线.由图可以看出，当h＝1时，即数学单元为正方形时，相对误差能量范数达到了10-16的机器精度；随着h的增加或减少，相对误差能量范数逐渐增加，当h＝1.5 时 达 到3.5‰，当h＝0.5 时 达 到2.2%.

图9 相对误差能量范数随h的变化曲线Fig.9 Variation of relative error in energy norm with respect to h

保持h＝0.8不变，将原物理单元细划成M×M个相同的矩形积分子域，每个子域仍采用2×2 点Gauss积分求单元刚度矩阵.如图10所示给出了相对误差能量范数随物理单元单边细化次数M 的变化曲线.由图可以看出，随着M 的增加，相对误差能量范数以几乎恒定的速率迅速降低，当M＝5时的相对误差能量范数仅为M＝1 时的1.7‰.计算结果进一步证明了刚度矩阵的数值计算误差是导致分片试验失败的原因.

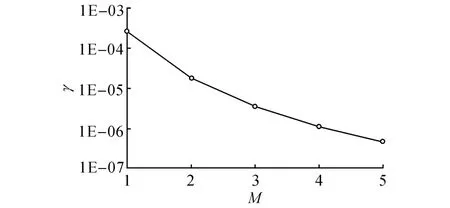
图10 相对误差能量范数随M 的变化曲线Fig.10 Variation of relative error in energy norm with respect to M

算例3 为验证细化积分子域对非连续分片试验的影响，将图5（c）示模型中的含裂纹物理单元细化为M×M 个积分子域，当M＝2时的积分子域划分如图11所示.

如表4所示给出了不同M 值时应力相对误差指标计算结果.由表可见，随着细化次数的增加，应力计算精度明显提高.

图11 当M＝2时物理单元积分子域划分Fig.11 Subdomain partition of physical elements when M＝2

表4 不同细化次数时应力相对误差指标Tab.4 Relative errors indexes of stresses with different Ms

5 结 论

本文以增强有限单元法为例，对Hansbo 和Hansbo类有限单元法进行了非连续分片试验，理论和数值分析了不能以机器精度通过分片试验的原因，得到如下结论：

（1）采用3节点三角形数学单元的网格能以机器精度通过分片试验；除少数特殊情况外，采用4节点四边形数学单元的网格不能以机器精度通过分片测试.

（2）数学单元与物理单元分离使得Hansbo和Hansbo类有限单元法具有表征单元内部非连续变形的能力.然而，对于四边形数学单元，数学单元与物理单元分离同时也使得刚度矩阵积分式中被积函数更为复杂，一般的三角形子域积分技术可能进一步降低刚度矩阵的积分精度，导致单元不能以机器精度通过非连续分片试验.

（3）为保证高精度通过非连续分片试验，合理的方法是在非连续变形区域采用三角形或平行四边形数学单元，或将与数学单元不完全重合的物理单元精细划分成积分子域以提高单元刚度矩阵的计算精度.需要指出，这些方法仅是从技术上提高了计算精度，若要从根本上解决问题，需要一种无网格依赖性的积分方法，这有待进一步研究.

（

）：

［1］AKSOYLU B，BOND S，HOLST M.An odyssey into local refinement and multilevel preconditioning III：Implementation and numerical experiments ［J］.SIAM Journal on Scientific Computing，2003，25（2）：478-498.

［2］ZHAO X，MAO S，SHI Z.Adaptive Finite Element Methods on quadrilateral meshes without hanging nodes［J］.SIAM Journal on Scientific Computing，2010，32（4）：2099-2120.

［3］SHI G H.Manifold method of material analysis［C］∥Transactions of the 9th army conference on applied mathematics and computing.Minneapolis，Minnesota：［s.n］，1991：57-76.

［4］位伟，姜清辉，周创兵.基于有限变形理论的数值流形方法研究［J］.力学学报，2014，46（1）：78-86.WEI Wei，JIANG Qing-hui，ZHOU Chuang-bing.Study on numerical manifold method based on finite deformation theory［J］.Chinese Journal of Theoretical and Applied Mechanics，2014，46（1）：78-86.

［5］徐栋栋，郑宏，夏开文，等.高阶扩展数值流形法在裂纹扩展中的应用.岩石力学与工程学报［J］，2014，33（7）：1375-1387.XU Dong-dong，ZHENG Hong，XIA Kai-wen，et al.Application of higher-order enriched numerical manifold method to crack propagation［J］.Chinese Journal of Rock Mechanics and Engineering，2014，33（7）：1375-1387.

［6］苏海东，祁勇峰，龚亚琦，等.任意形状覆盖的数值流形方法初步研究.长江科学院院报［J］，2013，30（12）：91-96.SU Hai-dong，QI Yong-feng，GONG Ya-qi，et al.Preliminary research of numerical manifold method based on covers of arbitrary shape［J］.Journal of Yangtze River Scientific Research Institute，2013，30（12）：91-96.

［7］BABUŠ KA I，MELENK J M.The partition of unity method［J］.International Journal for Numerical methods in Engineering，1997，40（4）：727-758.

［8］MOËS N，DOLBOW J，BELYTSCHKO T.A finite element method for crack growth without remeshing［J］.International Journal for Numerical Methods in Engineering，1999，46：131-150.

［9］BELYTSCHKO T，BLACK T.Elastic crack growth in finite elements with minimal remeshing［J］.International Journal for Numerical Methods in Engineering，1999，45：601-620.

［10］杨志锋，周昌玉，代巧.基于扩展有限元法的弹塑性裂纹扩展研究.南京工业大学学报：自然科学版［J］，2014，36（4）：50-57.YANG Zhi-feng，ZHOU Chang-yu，DAI Qiao.Elasticplastic crack propagation based on extended finite element method［J］.Journal of Nanjing University of Technology：Natural Science Edition，2014，36（4）：50-57.

［11］师访，高峰，杨玉贵.正交各向异性岩体裂纹扩展的扩展有限元方法研究［J］.岩土力学，2014，35（4）：1203-1210.SHI Fang，GAO Feng，YANG Yu-gui.Application of extended finite element method to study crack propagation problems of orthotr opic rock mass［J］.Rock and Soil Mechanics，2014，35（4）：1203-1210.

［12］HANSBO A，HANSBO P.A finite element method for the simulation of strong and weak discontinuities in solid mechanics［J］.Computer Methods in Applied Mechanics and Engineering，2004，193：3523-3540.

［13］HANSBO A，HANSBO P.An unfitted finite element method，based on Nitsche's method for elliptic interface problems［J］.Computer Methods in Applied Mechanics and Engineering，2002，191：5537-5552.

［14］AREIAS P，BELYTSCHKO T.A comment on the article“A finite element method for simulation of strong and weak discontinuities in solid mechanics”by A.Hansbo and P.Hansbo ［Comput.Methods Appl.Mech.Engrg.193（2004）3523–3540］［J］.Computer Methods in Applied Mechanics and Engineering，2006，195（9）：1275-1276.

［15］SONG J H，AREIAS P，BELYTSCHKO T.A method for dynamic crack and shear band propagation with phantom nodes［J］.International Journal for Numerical Methods in Engineering，2006，67（6）：868-893.

［16］LING D S，YANG Q D，COX B N.An augmented finite element method for modeling arbitrary discontinuities in composite materials［J］.International Journal of Fracture，2009，156（1）：53-73.

［17］凌道盛，卜令方，涂福彬.粘聚裂纹扩展的强化有限元h型网格自适应模拟［J］.计算力学学报，2014，31（2）：241-247.LING Dao-sheng，BU Ling-fang，TU Fu-bing.Modelling of cohesive crack propagation using enhanced finite element method via h-adaptive technique［J］.Chinese Journal of Computational Mechanics，2014，31（2）：241-247.

［18］LING D S，BU L F，TU F B，et al.A finite element method with mesh-separation based approximation technique and its application in modeling crack propagation with adaptive mesh refinement［J］.International Journal for Numerical Methods in Engineering，2014，99（7）：487-521.

［19］DOLBOW J E，DEVAN A.Enrichment of enhanced assumed strain approximations for representing strong discontinuities：addressing volumetric incompressibility and the discontinuous patch test［J］.International Journal for Numerical Methods in Engineering，2004，59：47-67.