钢板剪力墙单侧加劲肋的有效抗弯刚度

童根树，杨 章，张 磊

（浙江大学 土木工程学系，浙江 杭州310058）

加劲钢板已被广泛应用于桥梁、航空器和船舶结构，目前正在推广应用于高层建筑，即加劲钢板剪力墙.加劲钢板剪力墙与未加劲的钢板剪力墙相比，能够承受一定的竖向荷载，屈曲后的耗能能力更好，符合我国抗震设计的习惯.加劲肋的抗弯刚度对薄钢板剪力墙的剪切临界应力有很大影响.赵伟等［2］研究了加劲肋抗弯刚度对剪力墙弹性剪切临界应力影响的函数关系，并研究了使加劲肋之间的板块首先发生剪切屈曲（称为局部屈曲）的加劲肋最小刚度.

为了获得较好的经济指标，高层民用建筑钢结构设计规程建议采用单侧加劲肋.不同于双侧对称布置加劲肋的加劲板，单侧加劲板发生弯曲屈曲变形时，加劲肋弯曲的中和轴，既不在板件的中面，也不通过加劲肋的形心，位置取决于板件纵向刚度参与加劲肋工作的程度，这种参与程度通常采用板件的有效宽度来表示.即取板件的一部分宽度，与加劲肋一起组成一个新的截面，这个新截面（在加劲肋是板条时即为T 形截面）的抗弯刚度就是能够对板件起加劲作用的抗刚度.高层民用建筑钢结构设计规程建议加劲肋两侧各取15倍板厚参与加劲肋的工作.但是这个15倍板厚的做法来自于钢板屈曲后能够承受钢材屈服强度的有效宽度，并不是来自于加劲肋的有效刚度的计算.Schade［5］在上世纪50年代第1次对前面2种有效宽度做了区分.

对单侧加劲肋的有效抗弯刚度的研究方式主要分2种，1）通过研究有效宽度确定有效刚度，2）直接研究单侧加劲肋的有效刚度.

Karman［6］最早给出了无限宽度翼缘T 梁的有效宽度表达式.Schade［5］对布置多根单侧加劲肋的加劲板的有效宽度进行研究.Wang等［10-12］用数值方法和有限元模拟对特定结构的加劲板有效宽度做了研究.Seide［8］提出把单侧加劲肋等效为双侧加劲肋的等效刚度方法.Bedair等［9］采用能量法结合数值计算程序，研究了多根双侧和单侧加劲肋的刚度.

当前，单侧加劲肋的惯性矩计算的各种规范和建议并不一致［4］：美国规范AASHTO 以加劲肋和母板连接线为轴计算单侧加劲肋的惯性矩，中科院力学所板壳组和日本道路桥梁示方书等采用的是单侧加劲肋对母板中面的惯性矩，Bleich则建议单侧加劲肋有效宽度为30倍板厚.

用于屈曲分析的单侧加劲肋有效刚度是一个复杂的问题，无法得到一个能应用于不同领域的统一计算方法.目前，大部分的理论研究方法对象都是开口加劲肋，不考虑加劲肋剪切变形，数值解和有限元结果应用局限性比较大，而规范和建议的取值过于粗糙，由于缺乏理论分析，不能判定不同规范的规定是否总是偏于安全.本文针对建筑中钢板剪力墙布置单侧加劲肋的情况，将墙板和加劲肋离散成独立个体，采用力法分析板和加劲肋的变形，通过板肋连接处的变形连续条件建立屈曲方程.得到单侧加劲肋有效抗弯刚度的解析表达式，并给出刚度等效原则的有效宽度表达式，便于设计应用.

1 单侧加劲剪力墙轴压弹性屈曲

如图1所示为不同单侧加劲肋的有效截面，其中ts为加劲肋厚度，t为母板厚度，hs为加劲肋有效高度（板条加劲肋是板条底面到板中面距离，T 形和闭口加劲肋是翼缘中面到板中面距离），bs为加劲肋翼缘宽度，be为加劲板参与加劲肋工作的有效宽度.单侧加劲钢板剪力屈曲分析简化模型如图2（a）所示，长a，宽b，四边简支，居中布置单侧加劲肋，加劲肋与板件承受均布压应力σp.可设加劲板整体弹性屈曲挠度函数为

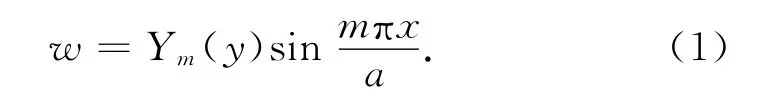
式中：w 为墙板平面外挠度，Ym（y）为墙板挠度y轴方向的形函数.m 为加劲板纵向屈曲半波数.

采用如下假定：1）小变形分析；2）墙板满足薄板理论的假定；3）加劲肋采用Timoshenko梁理论.

如图2（b）所示，对单侧加劲墙板隔离受力分析，闭口截面加劲板等效分割为槽型加劲肋和墙板.记Fsz为板和肋之间的z轴方向相互作用力，Fsx为板和肋之间的x 轴方向相互作用力，板1为墙板的一半.对肋和板1进行独立分析.

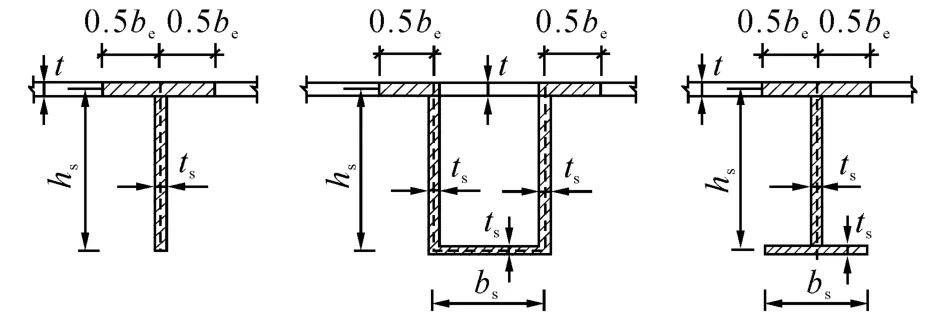
图1 单侧加劲肋的有效截面Fig.1 Effective section of one-side Stiffeners

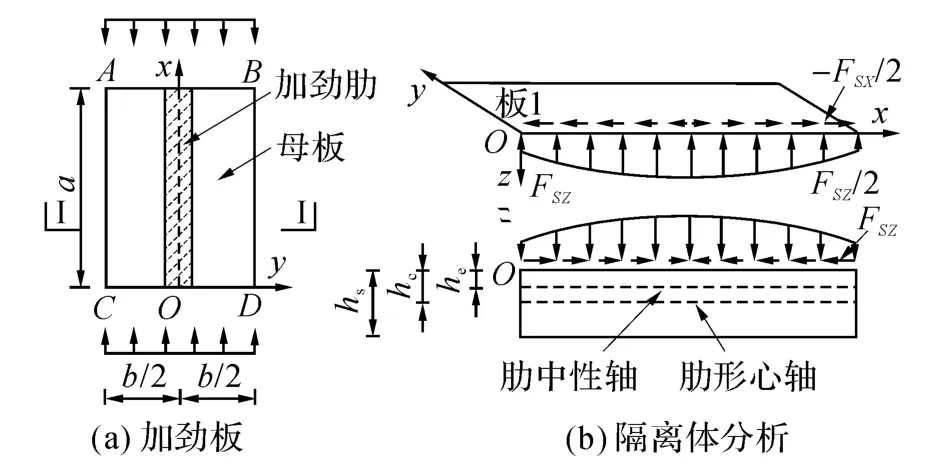
图2 加劲板及其隔离体分析Fig.2 Stiffened Plate and isolated analysis

1.1 加劲肋变形分析

加劲肋等效为简支梁，如图3所示.hc为加劲肋形心到被加劲板中面的距离，加劲肋弯曲挠度为

对应式（2）的弯曲挠度，Fsz和Fsx分布形式为

图3 加劲肋受力分析Fig.3 Stiffener analysis

式中：Azm、Axm为待定常数.Fsz对形心轴弯矩为

Fsx对形心轴的弯矩和等效形心轴轴力为

均布压应力产生的二阶弯矩为

式中：wst为加劲肋的剪切变形，As为加劲肋截面面积.且wst与wsb满足如下关系：

式中：Es、Gs为加劲肋材料的弹性模量和剪切模量，ks为有效截面剪切系数，Is，eff为加劲肋的有效惯性矩.由式（9）得到剪切变形为

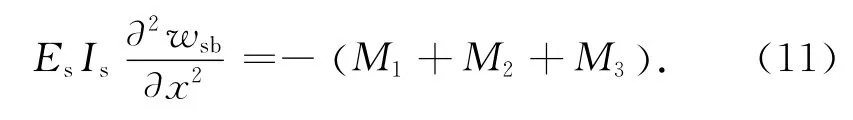
由式（5）、（6）、（7）、（8）、（10）、（11）可得加劲肋上边缘的z轴方向位移和x 轴方向应变：

图4 板1受力分析Fig.4 Plate analysis

1.2 板的平面应力分析

记板1 中面正应力为σx、σy，中面切应力为τxy，则存在满足平衡方程的应力函数φ，使得

板中面的平面应力问题相容方程为

参照屈曲波形的正弦变化规律，可设

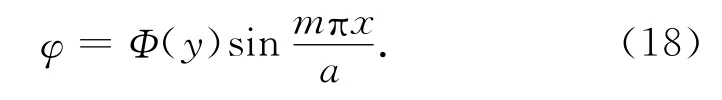
式中：Φ（y）为应力函数y轴方向的形函数.

将式（18）代入式（17）求解Φ（y）的微分方程，得到

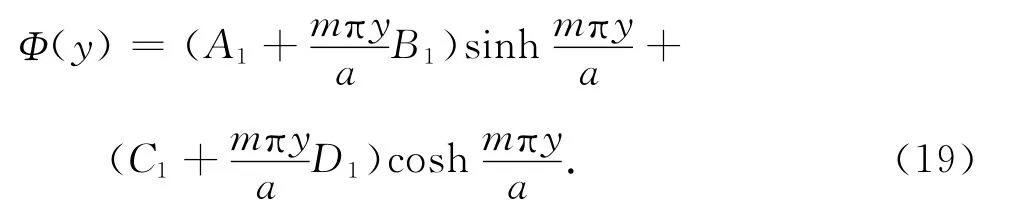
式中：A1、B1、C1、D1为待定系数.中面应力

式中：

记板1 中面正应变为εx、εy，中面切应变为εxy，E 为板弹性模量，μ 为板材料泊松比，则有

记板1中面x 和y 方向面内位移为u，v，则

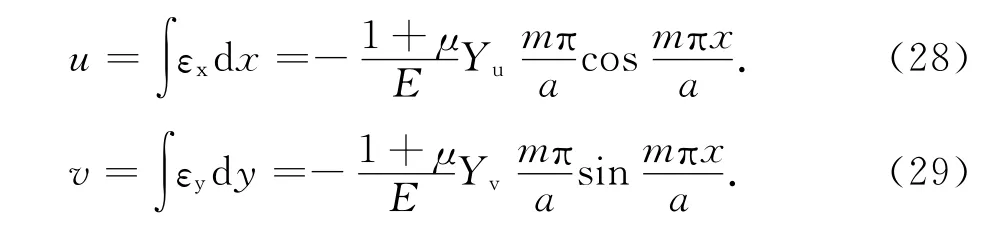
式中：

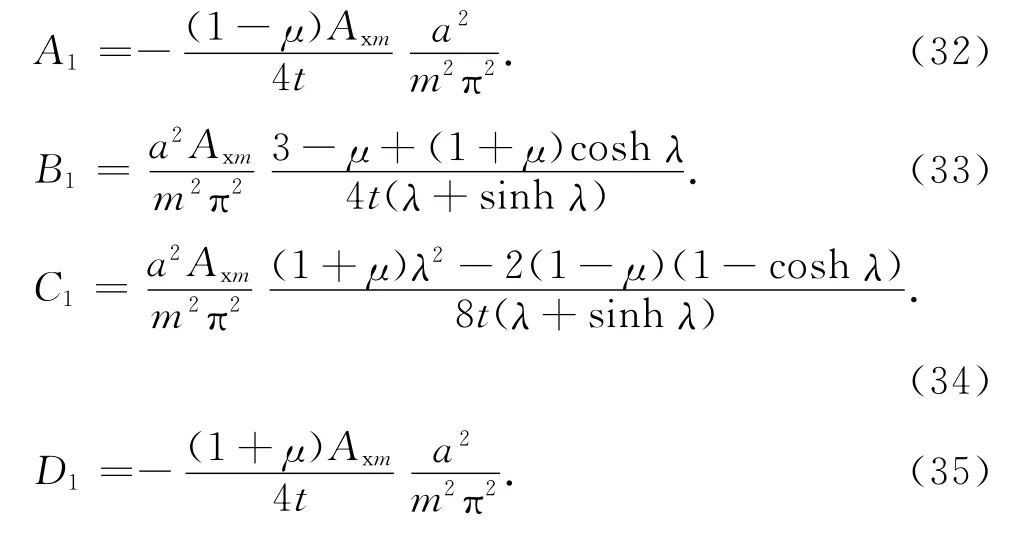
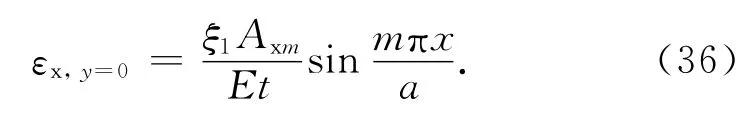
式中：

1.3 板的弯曲应力分析

板1的面外挠度w，满足平衡方程：

式中：A2，B2，C2，D2为待定系数，

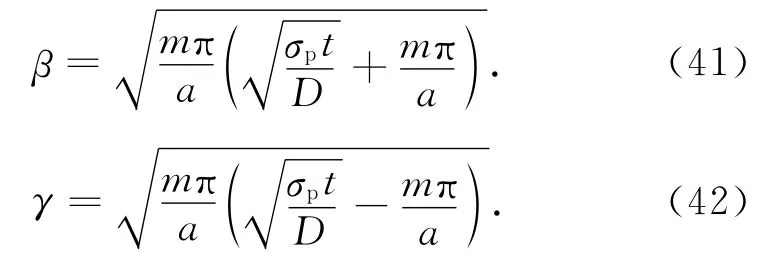
板加劲处中面的z方向挠度：

1.4 墙板与加劲肋的变形协调

板与肋在连接处挠度和x 方向应变相同，即

把式（12）、（13）、（36）、（47），代入方程（49）、（50），得到关于常系数Azm、Axm的方程组：

式中：

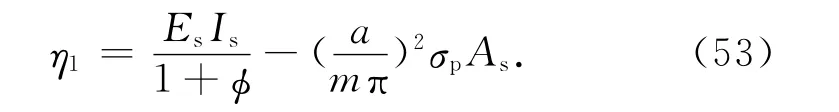
要使得板肋相互作用力Fsz、Fsx有非零解（即发生屈曲），则方程组的系数行列式等于零，从而得到屈曲临界方程：

其中，式（55）可以简化为

Timoshenko给出了不考虑剪切变形的对称加劲肋的屈曲临界方程［5］，以本文符号表示为

若同样考虑剪切变形则式（57）为

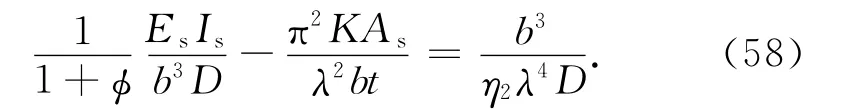
比较式（54）和（58）发现单侧加劲板和对称加劲板的屈曲临界方程非常相似，可以对单侧加劲肋取用有效惯性矩，从而把单侧加劲问题转化为对称加劲问题，单侧加劲肋有效惯性矩Is，eff表达式为

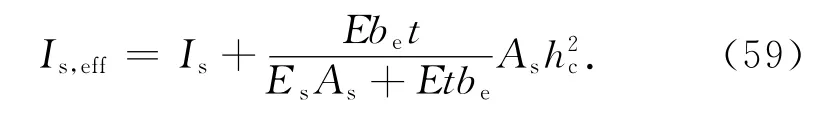
其中第2项即为偏心加劲效应带来的附加惯性矩.

2 面外荷载下的抗弯刚度

正弦弯曲波形下的抗弯刚度是其他弯曲变形分析的基础，故在加劲肋布置处施加z 方向正弦分布的外荷载为

式中：Bm为待定常系数.加劲板的挠度函数同式（1），同样对加劲板进行隔离体分析，如图5所示.

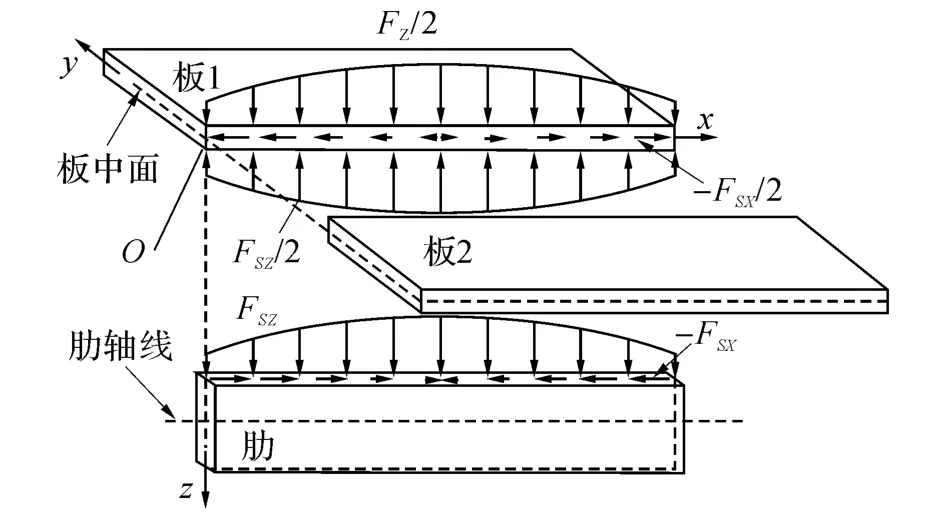
图5 加劲板受弯分析Fig.5 Discrete the open-form stiffened Plates

在面外荷载作用下，加劲肋的受力变形和屈曲分析基本相同，但无轴力及其二阶效应，肋上边缘的z轴方向位移和x 轴方向应变为

板加劲处中面x 轴方向应变表达式同式（36）.

板1的面外挠度w，满足平衡方程：

式中：A3、B3、C3、D3为待定系数.

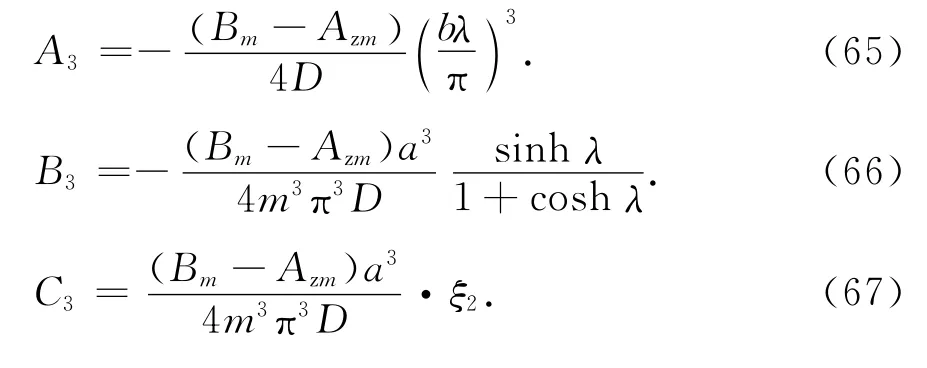
式中：

如图6所示为ξ1、ξ2 和板弯曲半波长宽比关系.

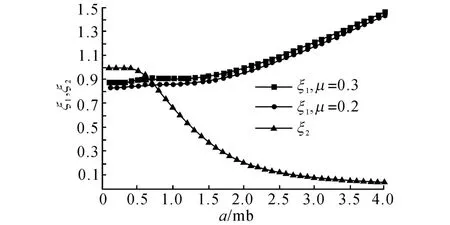
图6 、 和加劲板半波长宽比关系Fig.6 、ξ2change by aspect ratio of plate

板加劲处中面的挠度为

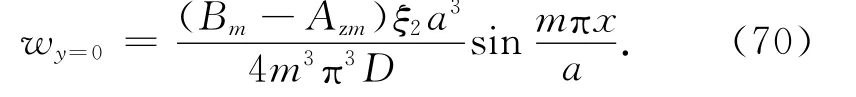
把式（61）、（62）、（36）、（70）代入方程（49）、（50），可以求得面外荷载和加劲肋挠度的关系：

式中：Bps为正弦弯曲波形下加劲板的抗弯刚度.

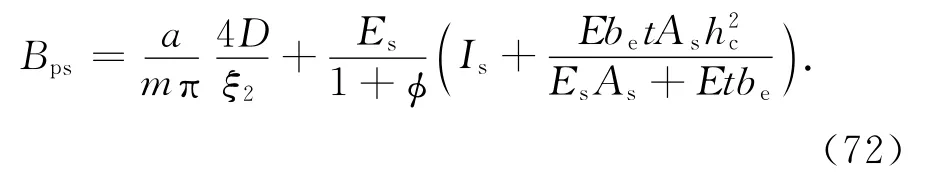
从式（72）的组成看，第1项是墙板本身提供的抗弯刚度，第2项即为加劲肋提供的抗弯刚度.和屈曲分析的结果比较发现，2种荷载形式下加劲肋的有效惯性矩的表达式相同，即有效宽度由弯曲变形形状决定.

3 加劲肋截面剪切系数

在Timoshenko梁理论中，按截面能量等效原则计算加权平均剪切应变角.单侧板条加劲肋有效截面为T 形截面，但其中的翼缘板即有效宽度部分墙板的剪切变形已在板件平面弯曲分析中得到考虑，只需计算腹板部分剪切变形.因此：

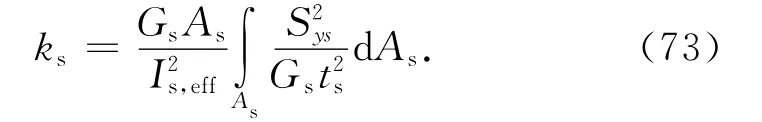
式中：Sys为对加劲肋中性轴的截面静矩，中性轴为加劲肋中应力为0的轴，记he为加劲肋中性轴到被加劲板中面距离，则

可推导求得he为

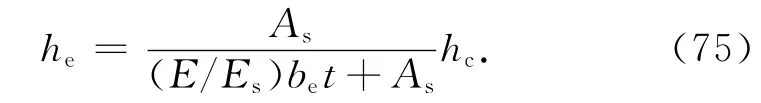
把式（75）代入式（59），简化为

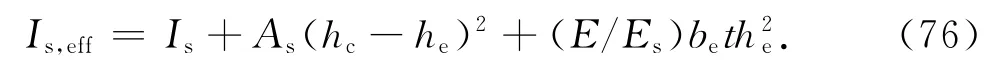
板条加劲肋的截面剪切系数为

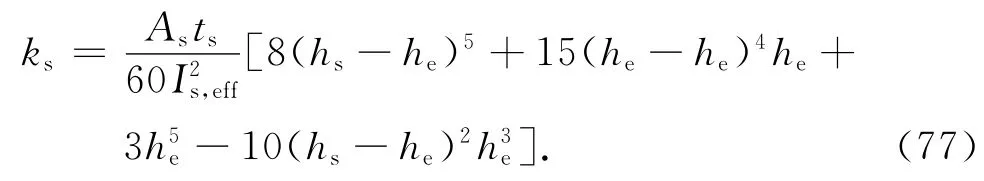
T 形加劲肋的截面剪切系数为

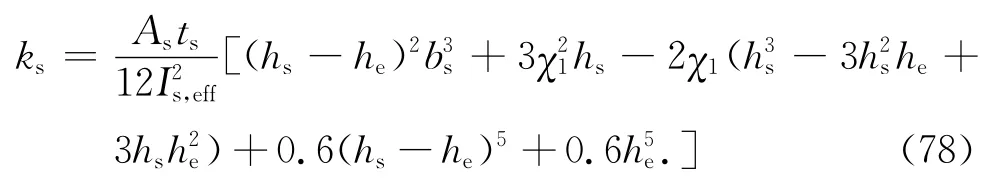
式中：χ1 ＝2bs（hs-he）＋（hs-he）2.

闭口加劲肋的截面剪切形状系数为

式中：χ2 ＝bs（hs-he）＋（hs-he）2.

如图7、8、9所示给出了一定尺寸的板条，T 形、闭口加劲肋截面剪刀形状系数和加劲助高跨此关系.

图7 板条加劲肋截面剪切形状系数Fig.7 Shear factor of plate-strip Stiffeners

4 ANSYS结果分析比对

采用有限元软件ANSYS进行分析比对.模型分别选用板条加劲肋、T 形加劲肋和闭口加劲肋.选用不同的板长宽比、肋跨高比、板和肋厚度比和翼缘宽和腹板高比.母板和加劲肋均采用shell63单元，母板的网格划分为60×60和80×80为主，网格划分使计算结果差别小于0.1%.加劲板四边简支，加劲肋两端简支，μs ＝μ＝0.3，Es＝E ＝2×105.

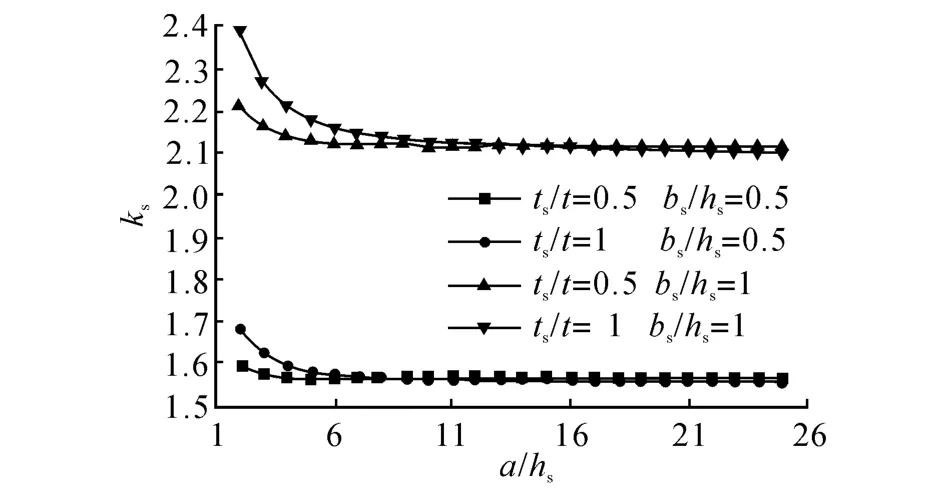
图8 T形加劲肋截面剪切形状系数（λ＝π）Fig.8 Shear factor for T-Stiffeners（λ＝π）

图9 闭口加劲肋截面剪切形状系数（λ＝π）Fig.9 Shear factor for closed-form Stiffeners（λ＝π）

当屈曲分析时，压应力施加在加载边的节点上，中间各点节点力相同，两端端点荷载为中间各点的一半.当面外荷载分析时，模型荷载施加在连接线上的节点上，节点力大小为正弦分布.

现给出母板宽厚比为100 的加劲板的理论和ANSYS数值分析结果对比如下：

4.1 屈曲系数结果对比

板条加劲墙板理论和Ansys的屈曲系数结果对比如表1 所示，其中，ERR 为相对误差，ERR＝（理论值-Ansys值）／Ansys值×100%，T形劲墙板理论和Ansys的屈曲系数结果对比如表2所示，对单侧闭口加劲肋板，Is，As计算截面为槽型截面，根据式（55）计算有效宽度.得到的结果如表3所示.

表1 板条单侧加劲板屈曲系数Tab.1 Buckling factor of plates stiffened by ne-side strip

表2 T形肋单侧加劲板屈曲系数Tab.2 Buckling factor of plates stiffened by T stiffener

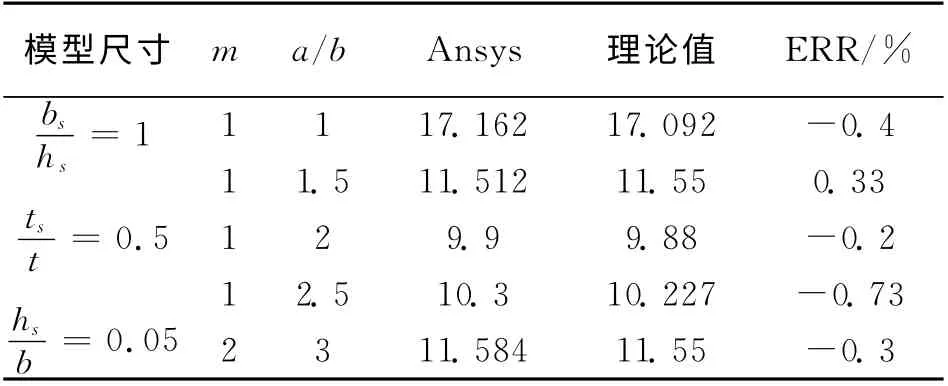
表3 闭口肋单侧加劲板屈曲系数Tab.3 Buckling factor of plates stiffened by one-side closed form stiffener

4.2 面外荷载下的抗弯刚度结果比对

板条、T 形和闭口加劲肋钢板面外荷载下有效抗弯刚度的理论值和Ansys值对比结果分别为如图10～12所示，纵坐标为加劲肋的有效刚度和自身刚度之比，横坐标为加劲肋跨高比，加劲肋剪切变形随跨高比变小而变大，从图10～12可以看出理论值和Ansys值非常接近，两者相对误差不随加劲肋跨高比而变化，说明剪切变形得到了正确计算.闭口截面加劲助Is、As计算截面为槽型截面，从图12可以看出，式（59）的有效惯性矩表达式能很好地应用于闭口截面.

5 结 论

本文对被加劲钢板发生屈曲时，单侧加劲肋参与抵抗屈曲的有效抗弯刚度进行研究.加劲肋可以是板条、T 形截面和闭口截面加劲肋，墙板是有限宽度的.得到的结论如下：

图10 板条加劲肋结果比对Fig.10 comparison of plate-strip Stiffeners

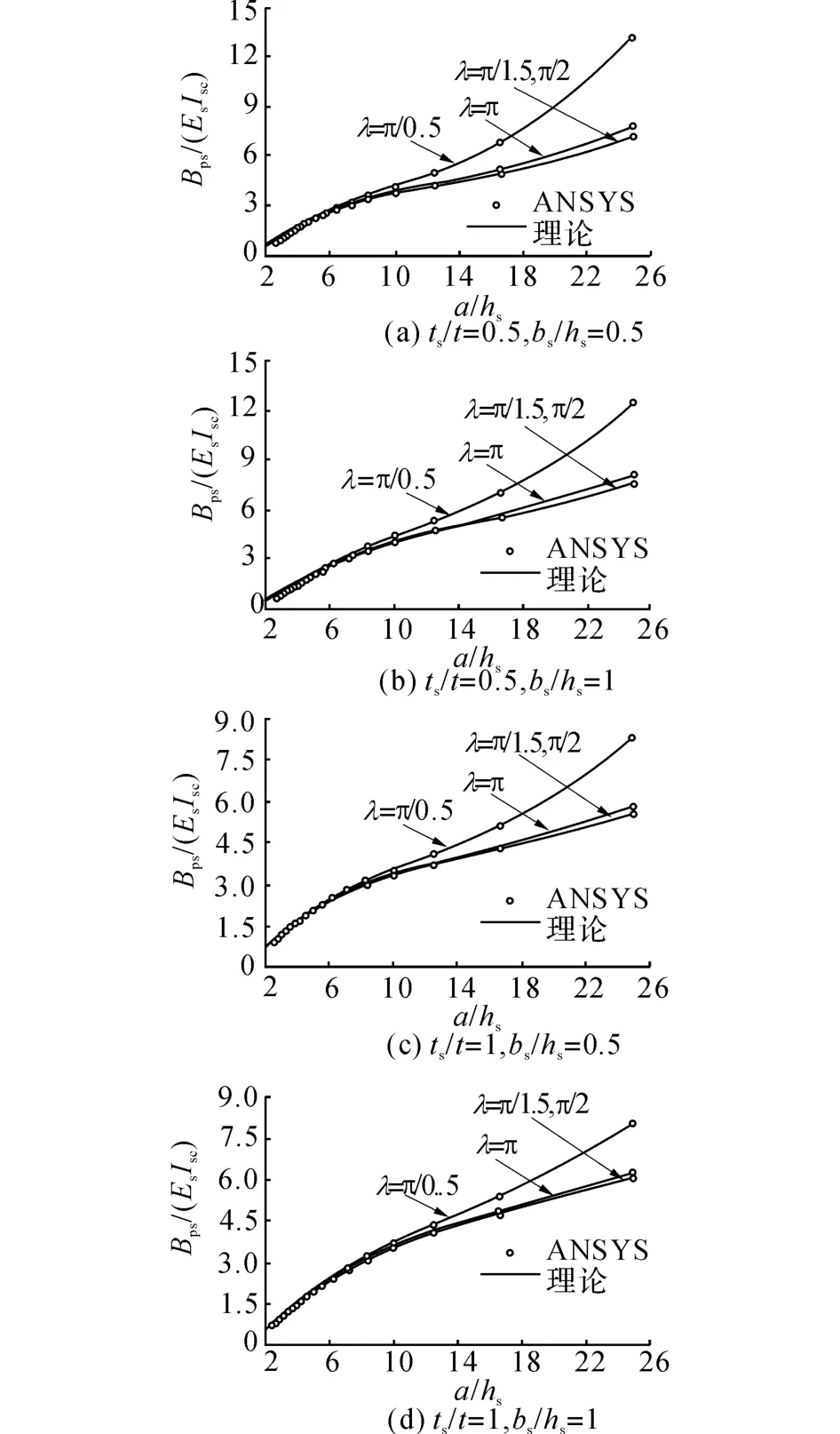
图11 T形加劲肋结果比对Fig.11 Comparison of T-Stiffener

图12 闭口加劲肋结果比对Fig.12 comparison for closed-form Stiffeners

（1）获得了单侧加劲板有效宽度的解析式.结果表明，有效宽度与板屈曲半波长和宽度的比值有关.考虑到墙板屈曲半波长又与加劲肋的有效刚度有关，加劲肋的有效刚度在研究加劲板屈曲的过程中才能加以确定.

（2）计算加劲肋等效惯性矩的中性轴位置介于板中面和肋形心轴之间.以板中面为中性轴来计算加劲肋的有效刚度，会使得惯性矩偏大.

（3）当加劲肋高跨比较大时，剪切变形影响不可忽略.Sapountzakis和沈嘉嘉［3］通过数值方法和有限元软件分析发现有效宽度受加劲肋高度和母板厚度影响，原因就在于剪切变形.这也是目前各国规范和建议都没有考虑的因素.

（4）计算加劲肋剪切变形的有效截面不包括有效宽度的板件，同时要根据真实的中性轴位置计算截面剪切系数.

（5）与有限元分析结果的比较表明，本文对3种截面形状的加劲肋得到的有效刚度公式均具有很好的精度.

（

）：

［1］沈金，干钢，童根树.钢板剪力墙设计与施工的工程实例［J］.建筑结构，2013，43（15）：19-22.SHEN Jin，GAN Gang，TONG Gen-shu.Practical application of design and construction of steel shear walls.［J］.Building Structure，2013，43（15）：19-22.

［2］赵伟，杨强跃，童根树.钢板剪力墙加劲肋刚度及弹性临界应力研究［J］.工程力学，2010，27（6）：15-23.Zhao wei，Yang qiangyue，Tong genshu.Stiffener stiffness and elastic buckling stress of steel plate shear wall［J］.Engineer-ing Mechanics，2010，27（6）：15-23.

［3］沈嘉嘉.考虑加劲肋扭转效应的加劲板在轴压下的弹性屈曲研究［D］.杭州：浙江大学，2014.SHEN Jia-jia.Buckling of stiffened plate under uniform compression with stiffener torision include［D］.Hang zhou：Zhejiang University，2014.

［4］吴炜.钢桥受压加劲板稳定与加劲肋设计方法研究［D］.上海：同济大学，2006.WU Wei，Stability of stiffened compression plates of steel bridge and stiffeners design method［D］.Shanghai：Tongji University，2006.

［5］SCHADE H A.The effective breadth of stiffened plating under bend loads［J］.Journal of Marine Science and Technology，1951 59：154-182.

［6］TIMOSHENKO S P，GOODIER J N.Theory of Elasticity［M］.New York：McGraw-Hill Book Company，1951：171-177.

［7］BULSON P S.The stability of flat plates［M］.London：Chatto＆Windus Ltd.1970：220-221.

［8］Seide.Paul.The effect of longitudinal stiffeners located on one side of plate on the compressive buckling stress of the plate-stiffener combination［R］.note 2873 Washing-ton DC：NACA，1953.

［9］BEDAIR O K.A contribution to stability of stiffened plates under uniform compression ［J ］.Computers＆Structures，1998，66（5）：535-570.

［10］WANG X，RAMMERSTORFER F G.Determination of effective breadth and effective width of stiffened plates by finite stripe analyses［J］.Thin-Walled Strictures，1996，26（4）：261-286.

［11］KATSIKADELIS J T，SAPOUNTZAKIS E.A realistic estimation of the effective breadth of ribbed plates［J］.International Journal of Solids and Structures，2002，39（4）：789-799.

［12］TIGAS I G，THEODOULIDES A.On the effective breadth of plating［M］.London：Taylor＆Francis Group，2012.