迹逼近C*-代数的可除和比较性质
2015-07-10方燕
方燕
(上海海事大学 文理学院, 上海 201306)
迹逼近C*-代数的可除和比较性质
方燕
(上海海事大学 文理学院, 上海 201306)
考虑一类有单位元的C*-代数(记为Ω)具有某种性质时,Ω中C*-代数迹逼近后得到的一类C*-代数(记为TAΩ)是否也具有这种性质.得出结论:若对∀B∈Ω,B的投影半群V(B)具有m-n几乎可除性质,则对∀A∈TAΩ,A的投影半群V(A)具有m+1-n几乎可除性质;若对∀B∈Ω,B具有强的迹m-投影比较性质,则对∀A∈TAΩ,A具有强的迹m-投影比较性质.
C*-代数; 迹逼近;K-半群
0 引 言
用K-群作为不变量对顺从的C*-代数进行分类,最先是由ELLIOTT[1]提出的.之后发现许多类C*-代数都可以用K-群进行分类.[2-4]研究者们逐渐发现迹态空间及其与K-群的配对也是C*-代数的分类必要不变量.比较重要的一类C*-代数是单的维数缓慢增长的AH-代数[5-6],可以用迹态空间与K-群的配对分类,通常称此不变量为ELLIOTT不变量.LIN[7]给出单的维数缓慢增长的AH-代数的公理化定义,称之为迹逼近区间C*-代数.受此启发,ELLIOTT等考虑一般的迹逼近C*-代数的概念.一个有单位元的C*-代数A∈TAΩ,是指对∀ε>0,任意的有限子集F⊆A,任意的非零正元b,存在一个非零投影p∈A和C*-子代数B⊆A,使得1B=p和B∈Ω,且有:(1)对∀x∈F,‖xp-px‖<ε; (2)对∀x∈F,pxp∈εB;(3)[1-p]≤[b].
考虑Ω类中C*-代数具有某种性质,TAΩ类中的C*-代数是否也具有这种性质,是一个重要且有意义的事情.事实上ELLIOTT等[8],FAN[9]和范庆斋等[10]都证明Ω类中C*-代数的许多分类性质可以遗传到TAΩ类中,且用它来证明C*-代数的分类定理.
本文证明: 如果Ω是一类C*-代数并且对∀B∈Ω,B的投影半群V(B)具有m-n几乎可除性质,则对于任意的C*-代数A∈TAΩ,A的投影半群V(A)具有m+1-n几乎可除性质.设Ω是一类C*-代数,且对∀B∈Ω,B具有强的迹m-投影比较性质,则对∀A∈TAΩ,A具有强的迹m-投影性质.
1 预备知识
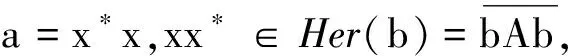
定义1.1[8]一个有单位元的C*-代数A∈TAΩ,是指对∀ε>0,任意的有限子集F⊆A,任意的非零正元b,存在一个非零投影p∈A和C*-子代数B⊆A,使得1B=p和B∈Ω,且有:
(1)对∀x∈F,‖xp-px‖<ε;
(2)对∀x∈F,pxp∈εB;
(3)[1-p]≤[b].
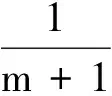
定义1.3[4,11]A是一个有单位元的C*-代数,称A具有m-几乎可除性质.若proj(M∞(A))表示M∞(A)中投影的全体,对∀p∈proj(M∞(A)),存在q∈proj(M∞(A))满足kq≤p≤(k+1)(m+1)q.
2 主要结果
定理2.1 设Ω是一类C*-代数,且对∀B∈Ω,B的投影半群V(B)具有m-k几乎可除性质,则对于任意的C*-代数A∈TAΩ,A的投影半群V(A)具有m+1-k几乎可除性质.
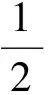
(1)‖pr-rp‖<ε;
(2)rpr∈εB.
由(1)和(2)存在投影p1∈B和p2∈(1-r)A·(1-r)满足‖p-p1-p2‖<ε,得[p]=[p1]+[p2].因为p1∈B且B∈Ω,所以存在q1∈B满足kq1≤p1≤(k+1)(m+1)q1.对于p2∈(1-r)A(1-r),因为(1-r)A(1-r)∈TAΩ,所以存在投影s和一个C*-子代数C满足C∈Ω,1C=S,使得
(1)‖p2s-sp2‖<ε;
(2)sp2s∈εC;
(3)[1-r-s]≤2[q1].
由(1)和(2)存在投影p3∈C和p4∈(1-r-s)A(1-r-s)满足‖p2-p3-p4‖<ε,得[p2]=[p3]+[p4].因为p3∈C且C∈Ω,所以存在q3∈C满足kq3≤p3≤(k+1)(m+1)q3.因为[p4]≤[1-r-s]≤[q1],所以
[q]=[q1]+[q2]=[q1]+[q3]+[q4]
[p]=[p1]+[p2]=[p1]+[p3]+[p4]
且
k[p]=k([p1]+[p2])=k([p1]+[p3]+[p4])≤[q1]+[q3]+k[q4]≤[q1]+[q3]+ [1-r-s]≤[q1]+[q3]+[q1]≤(k+1)· (m+1)[p1]+(k+1)(m+1)[p3]+[q1]
证明下面定理的方法和技巧来自文献[8]中的定理3.7.2.
定理2.2 设Ω是一类C*-代数,且对∀B∈Ω,B具有强的迹m-投影比较性质,则对∀A∈TAΩ,A具有强的迹m-投影性质.
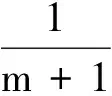
(1)对∀x∈F,‖rnx-xrn‖<ε;
(2)rnxrn∈Bn;
(3)[1-rn]≤[e].
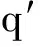
‖p-p′-p″‖∈εn
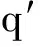
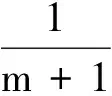
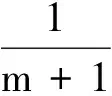
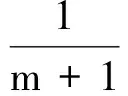
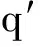
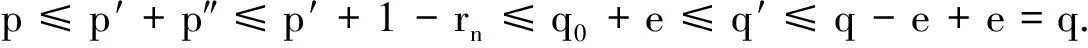
[1]ELLIOTT G A. On the classification of the inductive limits of sequences of semisimple finite dimensional algebras[J]. J Algeb, 1976, 38: 29-44.
[2]LIN H. The tracial topological rank ofC*-algebras[J]. Proc London Math Soc, 2001, 83: 199-234.
[3]NIU Z. A classification of certain tracially approximately subhomogeneousC*-algebras[D]. Canada: University of Toronto, 2005.
[4]WINTER W. Nuclear dimension and Z-stability of pureC*-algebras[J]. Invent Math, 2012, 187: 259-342.
[5]ELLIOTT G A, GONG G. On the classification ofC*-algebras of real rank zero II[J]. Ann Math, 1996, 144: 497-610.
[6]ELLIOTT G A. On the classification ofC*-algebras of real rank zero[J]. J Reine Angew Math, 1993, 443: 179-219.
[7]LIN H. An introduction to the classification of amenableC*-algebras[M]. New Jersey: World Scientific, 2001.
[8]ELLIOTT G A, NIU Z. On tracial approximation[J]. J Func Anal, 2008, 254: 396-440.
[9]FAN Q.K0-monoid properties preserved by tracial approximation[J]. J Operator Theory, 2013, 69: 101-109.
[10]范庆斋, 杨君. 迹逼近C*-代数的遗传性[J]. 上海海事大学学报, 2011, 32(2): 91-94.
[11]BLAKADAR B.K-theory for operator algebra[M]. New York: Springer-Verlag, 1986.
(编辑 贾裙平)
Division and comparison properties of tracial approximationC*-algebras
FANG Yan
(College of Arts & Sciences, Shanghai Maritime Univ., Shanghai 201306, China)
It is discussed that, if a class ofC*-algebras (denoted byΩ) with an identity element has a property, whether the class ofC*-algebras (denoted byTAΩ) that be tracially approximated byC*-algebras inΩhas the property. It is concluded that, if the projective semigroup ofB,V(B), has anm-nalmost divisible property for anyB∈Ω, the projective semigroup ofA,V(A), has anm+1-nalmost divisible property for anyA∈TAΩ; ifBhas a strong tracialm-comparison projection property for anyB∈Ω,Ahas also the property for anyA∈TAΩ.
C*-algebra; tracial approximation;K-semigroup
10.13340/j.jsmu.2015.03.017
1672-9498(2015)03-0100-03
2014-07-01
2015-03-17
上海市教育委员会科研创新项目(13YZ090)
方燕(1961—),女,云南昆明人,副教授,硕士,研究方向为泛函分析,(E-mail)yanfang@shmtu.edu.cn
O177.5
A
