考虑客户满意度的网购物流配送路径优化
2015-07-10赵锐胡雄何红弟
赵锐, 胡雄, 何红弟
(上海海事大学 科学研究院,上海 201306)
考虑客户满意度的网购物流配送路径优化
赵锐, 胡雄, 何红弟
(上海海事大学 科学研究院,上海 201306)
为更全面地反映网购物流配送的客户满意度, 引入客户满意度指标.首先,考虑城市交通管制的硬时间窗约束和客户要求的软时间窗约束,建立最小配送成本和最短配送时间的多目标优化模型;然后,引入客户满意度指标,并设定客户满意度阈值,对该模型进行优化.设计遗传算法求解该优化模型.结合实际算例对模型和算法的有效性进行验证.结果表明:优化后的模型可以在保证较低配送成本和较少配送时间的基础上,最大化配送服务的客户满意度水平.该方法不存在客户流失的风险,有利于提高企业的竞争优势,符合企业的长远利益.
客户满意度; 物流配送; 硬时间窗; 软时间窗; 遗传算法
0 引 言
随着计算机网络技术的创新和消费者消费观念的转变,电子商务得到突飞猛进的发展.电子商务的发展离不开现代物流的支撑,且物流配送路径的选择关系到企业的配送成本、配送效率和配送服务水平,因此对网购物流配送路径进行优化十分必要.
自DANTZIG等[1]首次提出车辆路径问题以来,该领域已取得非常丰富的研究成果.配送成本和配送时间是车辆路径问题的基本优化对象,该领域的研究起步较早.VIDAL等[2]研究有装载能力和路线约束的多节点车辆路径问题,并采用一种混合遗传算法(Genetic Algorithm,GA)进行求解.BATTARRA等[3]提出基于空间聚类车辆路径问题的整数目标规划模型,并采用分支切割算法求解.彭碧涛等[4]研究多时间窗车辆路径问题,首先利用基本蚁群算法进行求解,然后采用加入变异算子的元胞自动机算法对结果进行优化.DABIA等[5]通过选择在合适的时间为客户提供配送服务,减少配送所需时间和配送成本.胡继雪[6]研究基于车辆路径问题的配送分区优化问题,并采用“先分区,再排程,后改进”的三阶段算法进行求解.JIANG等[7]研究带时间窗的多车型车辆路径问题,并采用基于二阶段法的禁忌搜索算法进行求解,但是该算法容易陷于局部最优.随着客户对配送服务要求的提高,简单地对配送成本和配送时间进行优化已难以满足实际需求.胡云超等[8]对6种交通管制情境下的城市配送优化综合效益进行对比,发现城市货运交通管制政策会增加企业的配送成本,但具有较好的社会效益.陈文强等[9]考虑由时间延迟所造成的货物价值损失,对运输和装卸过程分别建模,然后联合求解总目标.
企业间的竞争不仅仅是价格的竞争,更是服务的竞争.何婵等[10]为衡量企业的服务水平,引入客户满意度指标.OLIVER等[11]认为当买到的产品与客户预期相符时即产生客户满意度.李逸珩[12]建立基于客户服务中心的运营商客户感知和外部评价与客户满意度内部管理相统一的客户满意度管理模型,形成可衡量的客户满意度评价体系.SZYMZNSKI等[13]认为在网络零售行业,服务属性可以驱动客户满意度.SINGH等[14]发现客户满意度对企业绩效有极其重要的影响,但客户满意度在物流配送领域的研究中比较有限.邓丽君[15]研究考虑客户满意度的物流配送车辆调度问题,并建立最小化运输成本和最大化客户满意度的多目标优化模型.
已有文献对成本和时间的优化及模型的求解研究得比较多,但是对衡量配送服务水平的客户满意度的研究比较少.在实际应用中,城市交通管制和回程取货等实际常见问题也容易被忽略.因此,对考虑客户满意度的网购物流配送优化问题进行研究具有重要的理论与现实意义.
1 问题描述与假设
顾客在线完成下单后由电商企业或第三方物流企业提供配送服务.配送车辆从配送中心出发,依次为分布在不同位置的客户提供配送服务,并最终回到配送中心.在满足客户货物需求量和供应量、车辆载质量限制、客户要求的服务时间和城市交通管制等约束的条件下,通过合理安排行驶路线,实现配送成本最小、配送时间最短、配送数量最大、利用资源最少等目标.结合网购的物流配送特点,作以下基本假设:
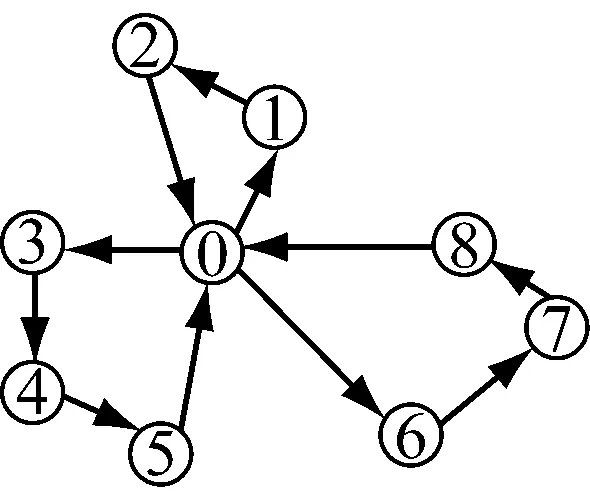
图1 车辆配送路径
(1)如图1所示,车辆从同一配送中心(0)驶出,同时提供送货和取货服务,最终回到配送中心.配送人员需要将物流跟踪信息及时通过终端传回总部.
(2)车辆为客户提供送货和取货服务时将产生货物处理时间和货物处理成本,这里的货物处理时间和成本与客户的货物量相关.
(3)每个客户的货物需求量和供应量均在车辆最大载质量范围内,不同货物可以根据需要混装,且每个客户只能由一辆车提供服务.
(4)交通管制时间窗内禁止所有车辆在限行区域内行驶.
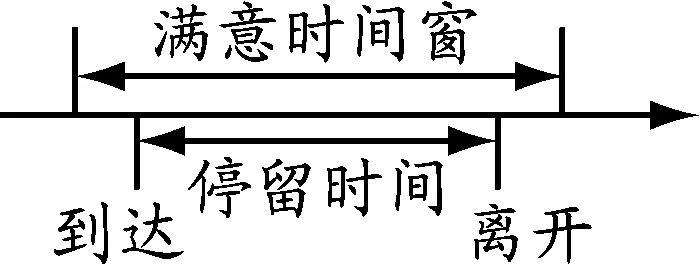
图2 满意时间窗内到达
(5)客户有服务时间窗要求,车辆需要在客户能够接受的时间窗内到达.车辆在客户满意时间窗内到达不会被惩罚,如图2所示;车辆在客户满意时间窗外到达则会有一定的时间惩罚,如图3所示.但以上情况均不影响车辆正常送货和取货.惩罚成本与车辆到达时间相关.
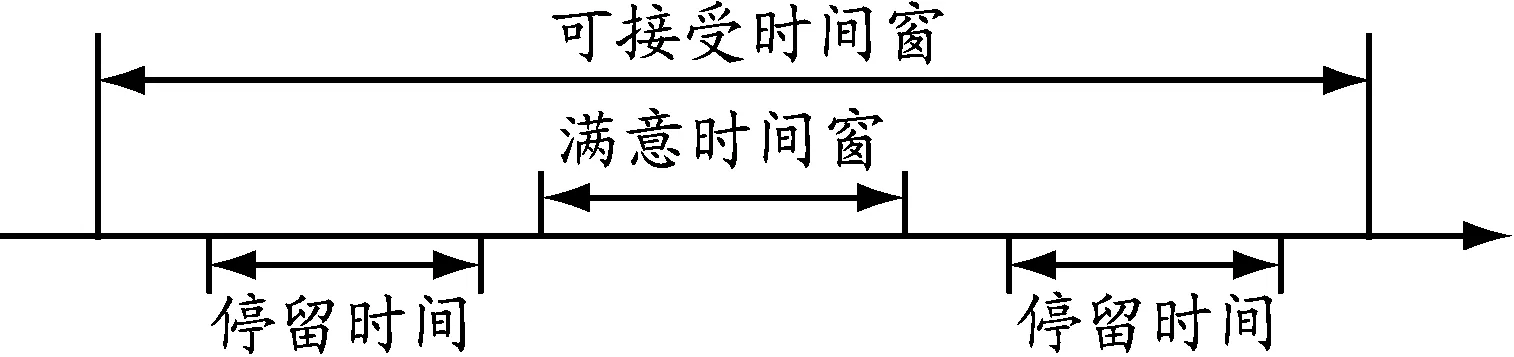
图3 可接受时间窗内到达
(6)配送中心的车辆有一定数量限制,要求服务车辆总数不多于该上限.[3]
(7)客户和配送中心的坐标位置,以及各客户的货物量均已在配送前确定.[15]
(8)所有车辆均有相同的行驶速度和最大载质量限制,且单位时间的运行成本相同.
(9)车辆只能在客户要求的时间窗内到达,不存在因提前到达而发生等待时间.不考虑红灯的等待时间,以及驾驶员的休息和用餐时间.
2 模型建立
在考虑客户时间要求和城市交通管制等约束的条件下,分别建立最小配送成本、最短配送时间和最大客户满意度的单目标优化模型,并通过加权处理形成可以求解的多目标优化模型.
2.1 最小配送成本模型
Z1=Z11+Z12+Z13,其中:Z11取决于车辆的行驶路线;Z12取决于客户总的货物需求量和供应量;Z13取决于车辆到达时间.最小配送成本模型为
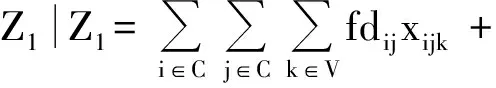
(1)
s. t.
(2)
(3)
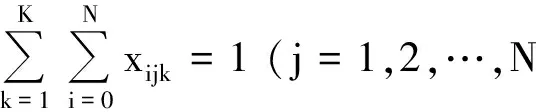
(4)
(5)
(6)
(7)
(k∈V;i,j∈C)
(8)
(9)
Di,Pi,dij,Tp,ik≥0
(10)
式(1)为最小配送成本模型的目标函数;式(2)为车辆在不同时刻到达客户点被惩罚的时间;式(3)表示由配送中心出发的车辆总数不超过K;式(4)表示每个客户只能由一辆车服务;式(5)表示全部车辆都是由配送中心出发,并最终回到配送中心的;式(6)和(7)分别对客户的需求量和供应量进行约束;式(8)指车辆只能从某一客户到另一客户;式(9)对每辆车服务的客户数进行约束;式(10)表示客户的货物需求量和供应量、客户点间的距离以及惩罚时间都是非负实数.
2.2 最短配送时间模型
Z2=Z21+Z22,其中:Z21取决于各客户的坐标位置和行驶路线选择;Z22取决于客户的货物需求量和供应量.最短配送时间模型为
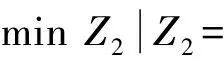
(11)
s. t.
tijk=dij/v
(12)
Td,ik-Ta,ik=T(Di+Pi)
(13)
Td,ik≤Ta,i+1,k
(14)
Qi-1,k+Pi-Di=Qik,
Qik≤R(i=1,2,…,N;k∈V)
(15)
Ta,ik≤Ls,Td,ik≤Ls,i∈Ctr;
或Ta,ik≥Le,Td,ik≥Le,i∈Ctr
(16)
Ta,ik,Td,ik,tijk,Tp,ik≥0
(17)
式(11)为最短配送时间模型的目标函数;式(12)表示车辆在各客户点间的行驶时间;式(13)表示车辆在各客户点的停留时间;式(14)表示只有服务完客户i才可以服务客户i+1;式(15)表示离开客户i的载质量取决于离开客户点i-1的载质量以及客户i的货物需求量和供应量;式(16)表示禁止车辆在交通管制时间内通行,交通管制政策增加了企业物流配送成本[8];式(17)表示车辆到达时间、离开时间、行驶时间以及惩罚时间都为非负实数.
2.3 最大客户满意度模型
当客户买到的产品或服务与预期相符即产生客户满意度.[11]本文从配送的准时性着手,建立最大客户满意度模型.考虑到不同客户的重要程度有差异[5],有必要对不同客户的满意度进行加权处理.设λi为客户i的客户满意度权重,其大小主要取决于客户i的货物量.最大客户满意度模型为
(18)
s. t.
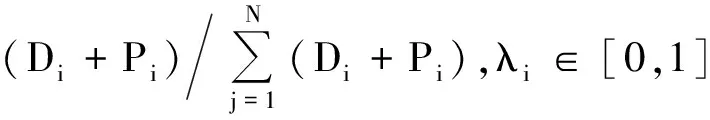
(19)
Fi(Ta,ik)=
(20)
式(18)为最大客户满意度模型的目标函数;式(19)为不同客户的满意度权重;式(20)是从车辆到达时间入手,形成可衡量的客户满意度评价体系[12].
2.4 最小配送成本和最短配送时间的多目标优化模型
通常建立多目标优化模型更符合实际.考虑到多目标函数的量纲并不统一,故运用极差法对目标函数进行无量纲化处理,其公式为
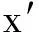
(21)
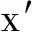
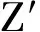

(22)
经过线性加权处理,将多目标优化问题转换为如式(22)所示的单目标优化问题.
2.5 考虑客户满意度的多目标优化模型
企业间的竞争已经从单一的价格竞争变成以价格和服务为一体的综合竞争,服务属性可以驱动客户满意度.[13]客户满意度对企业的绩效有重要影响[14],在物流配送行业尤为明显.物流服务水平直接影响客户对产品的需求.[10]因此,在原有模型的基础上引入客户满意度指标,建立最小配送成本、最短配送时间和最大客户满意度的多目标优化模型.对Z3取负号,求整体最小化.Z3的无量纲化处理公式为
3=-(Z3-minZ3)/(maxZ3-minZ3)
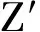
(23)
经过线性加权处理,将多目标优化问题转换为如式(23)所示的单目标优化问题.
3 模型求解算法设计
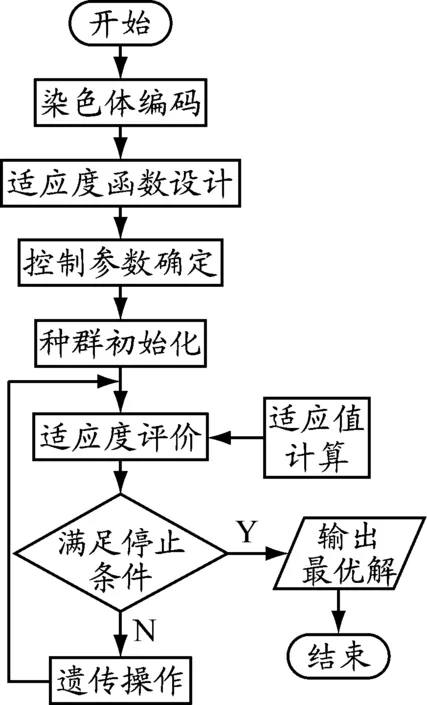
图4 简单GA的运算流程
GA是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法.[6]与禁忌搜索等算法相比,GA主要特点是可以对搜索空间中的多个解同时进行评估,减少陷于局部最优的风险.[7]与精确算法相比,GA求解过程耗时更短,适合于实际配送企业的决策.因此,GA在求解多目标优化问题中得到广泛应用.针对以上多目标优化模型的求解算法流程见图4.具体求解算法设计如下.
(1)染色体编码.求解车辆路径问题时,适合采用排列法进行编码来构造染色体.将配送中心和所有客户按连续的整数编号,由这些整数随机排列组成染色体,其中,0代表配送中心,1,2,…,N表示N个客户.如采用排列法构造染色体0-1-5-2-0-9-0-3-7-4-6-0-0,可理解为:第一辆车由配送中心出发,按“0-1-5-2-0”的路线行驶,分别为客户1,5,2提供送货和取货服务,最后回到配送中心;第二辆车按路径“0-9-0”提供送取货服务;第三辆车按路线“0-3-7-4-6-0”提供送取货服务;第四辆车停在配送中心.
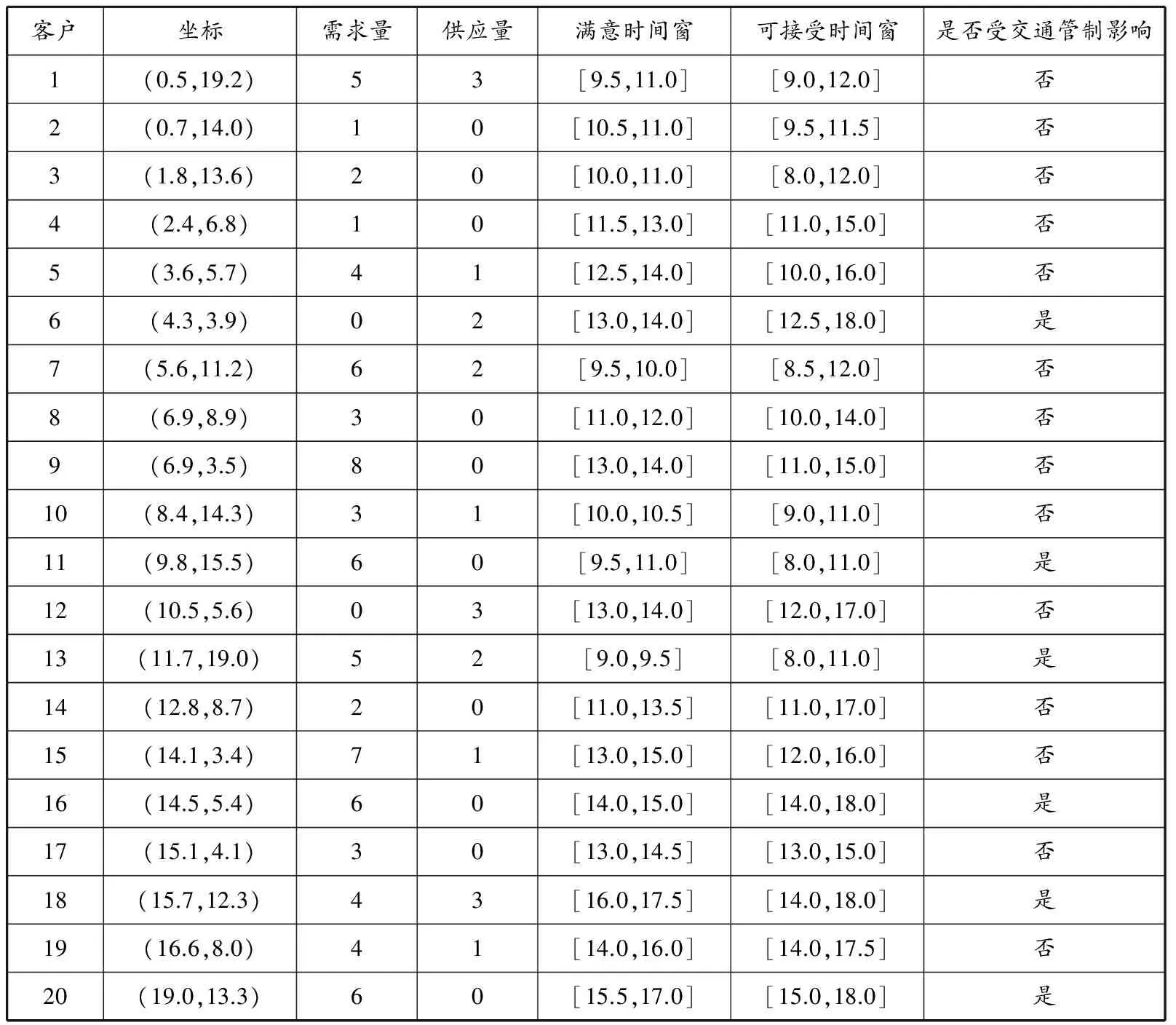
(2)初始种群设定.种群规模指群体中全部个体数量,初始种群的设定对算法的性能影响很大.为避免可能产生未成熟收敛和陷入局部最优的风险,可以先生成数字1至N,然后将N个随机排列的数字作为初始染色体表示N个客户的配送顺序,从而形成初始群体.
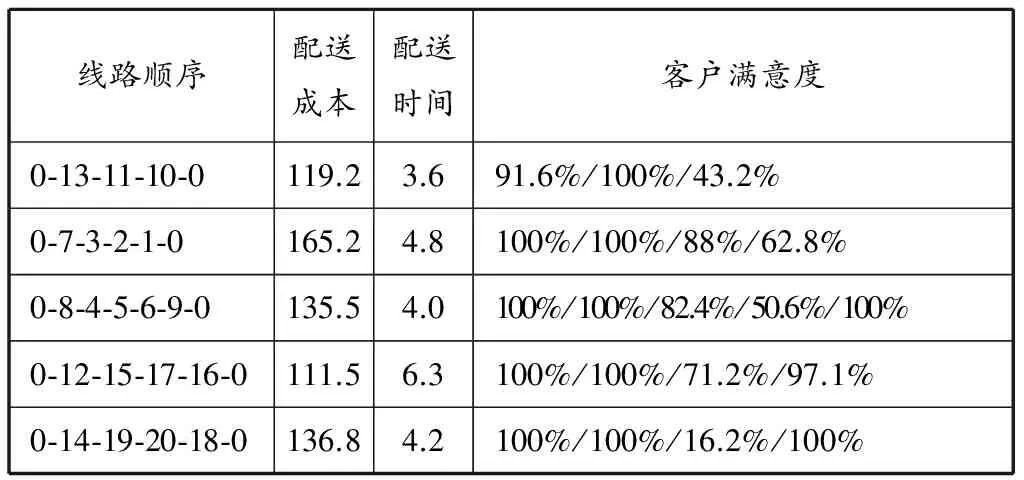
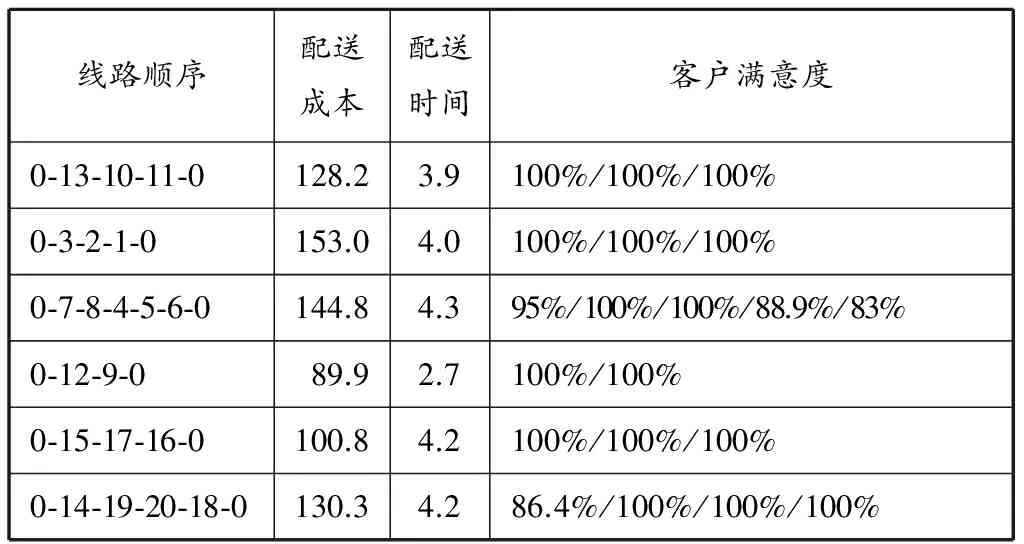
(3)适应度函数定义.首先需要将原始染色体处理成带有配送路径的染色体,也就是在考虑车辆载质量限制的情况下,在原始染色体中有序插入0,使其形成多个闭合的配送路径.如果最终使用的车辆数小于配送中心总的车辆数K,则需要在染色体的尾部补足0的数量.在对个体进行评价时,需要把每个染色体的目标函数值转换为相应的适应度值.对最小化问题,可建立目标函数与适应度函数的映射关系:f(x)=Cmax-g(x),g(x) (5)控制参数设定.控制参数的选择非常重要,它会影响整个算法的收敛性.在基本GA中,必须预先设定:①群体中全部个体的数量M,一般取10~200;②终止进化代数T,一般取50~500;③交叉概率Pc,一般取0.40~0.99;④变异概率Pm,一般取0.000 1~0.1. 客户的基本信息见表1.共有配送中心1个,其坐标为(10,10);客户点数N=20,所有客户在边长为20的矩形框内随机生成;K=6;R=20;dmax=30;v=10;f=5;H=2;cp=12;客户满意度阈值为80%;配送时间为[8,18];交通管制时间窗为[8.0,8.5]和[17.0,17.5],交通管制区域涵盖客户6,11,13,16,18和20. 算法中的控制参数设置为:M=20,T=50,Pc=0.6,Pm=0.01.模型的求解是使用MATLAB在Windows 7 (AMD Athlon(tm)Neo X2 Dual Core Processor L335 1.6 GHz)平台上编程实现的. 4.1 最小配送成本和最短配送时间的多目标优化模型 首先建立常规的最小配送成本和最短配送时间的多目标优化模型.采用GA求得的最优解对应的染色体是0-13-11-10-0-7-3-2-1-0-8-4-5-6-9-0-12-15-17-16-0-14-19-20-18-0-0,即共需安排5辆车提供配送服务.详细的求解结果见表2. 4.2 考虑客户满意度的多目标优化模型 在原有模型的基础上,建立最小配送成本、最短配送时间和最大客户满意度的多目标优化模型.采用GA求得的最优解对应的染色体是0-13-10-11-0-3-2-1-0-7-8-4-5-6-0-12-9-0-15-17-16-0-14-19-20-18-0,即共需安排6辆车提供配送服务.详细的求解结果见表3. 在原有模型中,平均每位客户的配送成本为33.4,配送时间为1.1,客户满意度为85.4%.但是客户10,1,6,17,20的满意度值均低于设定的客户满意度阈值80%,即面临客户流失的风险.在考虑客户满意度约束的优化模型中,平均每位客户的配送成本为37.6,配送时间为1.2,客户满意度为98.6%,且每位客户的满意度值均高于设定的客户满意度阈值80%,即不存在客户流失的风险.通过对比发现,虽然平均每位客户的配送成本增加4.2,配送时间增加0.1,但整体客户满意度水平提高13.2%,不存在客户流失的风险. 表1 客户的基本信息统计 表2 不考虑客户满意度的求解结果 表3 考虑客户满意度的求解结果 物流配送是电子商务的重要组成部分,高效的物流配送能够提高电商企业核心竞争力.本文首先建立最小配送成本和最短配送时间的多目标优化模型,并考虑到城市交通管制的硬时间窗约束和客户要求的软时间窗约束;然后引入客户满意度指标,并设定客户满意度阈值,对该模型进行优化;最后设计算法和算例对以上两个模型进行求解分析.原有模型可以保证较低的配送成本和较少的配送时间,但是部分客户满意度值较低,存在客户流失的风险.优化后的模型可以在保证较低配送成本和较少配送时间的基础上,最大化配送服务的客户满意度水平,不存在客户流失的风险,有利于提高企业的竞争优势,符合企业的长远利益. 机动车数量的不断增长给城市道路交通带来更多压力.进一步的研究将考虑配送车辆对城市道路交通环境的影响. [1]DANTZIG G B, RAMSER J H. The truck dispatching problem[J]. Manage Sci, 1959, 6(1): 80-91. [2]VIDAL T, CRAINIC T G, GENDREAU M,etal. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems[J]. Operations Res, 2012, 60(3): 611-624. [3]BATTARRA M, ERDOGAN G, VIGO D. Exact algorithms for the clustered vehicle routing problem[J]. Operations Res, 2014, 62(1): 58-71. [4]彭碧涛, 周永务. 多时间窗车辆路径问题的混合蚁群算法[J]. 计算机工程与应用, 2010, 46(31): 28-31. [5]DABIA S, ROPKE S, WOENSEL T V,etal. Branch and price for the time-dependent vehicle routing problem with time windows[J].Transportation Sci, 2013, 47(3): 380-396. [6]胡继雪. 基于大规模车辆路径问题的配送分区优化研究[D]. 济南: 山东大学, 2013. [7]JIANG J, NG K M, POH K L,etal. Vehicle routing problem with a heterogeneous fleet and time windows[J]. Expert Systems with Applications, 2014, 41: 3748-3760. [8]胡云超, 申金升, 黄爱玲. 城市货运交通管制情境下城市配送多目标优化效益研究[J]. 交通运输系统工程与信息, 2012, 12(6): 119-125. [9]陈文强, 顾玉磊. 基于货物时间价值的物流网络最优配送路径模型研究[J]. 交通运输工程与信息学报, 2013, 11(2): 19-23. [10]何婵, 刘伟, 崔爱平. 考虑物流服务水平影响的三级物流服务供应链协调[J]. 上海海事大学学报, 2014, 35(1): 41-48. [11]OLIVER R L, SWAN J E. Equity and disconfirmation perceptions as influences on merchant and product satisfaction[J]. J Consumer Res, 1989, 16(3): 372-383. [12]李逸珩. 基于客户服务中心的运营商客户满意度管理研究[D]. 武汉: 华中科技大学, 2012. [13]SZYMZNSKI D M, HISE R T. E-satisfaction: an initial examination[J]. J Retailing, 2000, 76(3): 309-322. [14]SINGH S, RANCHHOD A. Market orientation and customer satisfaction: evidence from British machine tool industry[J]. Ind Marketing Manage, 2004, 33: 135-144. [15]邓丽君. 基于客户满意度的物流配送车辆调度优化模型与算法研究[D]. 北京: 北京交通大学, 2012. (编辑 赵勉) E-commerce logistics distribution routing optimization considering customer satisfaction ZHAO Rui, HU Xiong, HE Hongdi (Academy of Science & Technology, Shanghai Maritime Univ., Shanghai 201306, China) In order to better reflect customer satisfaction in the process of e-commerce logistics distribution, the customer satisfaction index is introduced. First, a multi-objective optimization model is formulated with the minimal distribution cost and time under the hard time window constraint of urban traffic control and the soft time window constraint of customer requirements. Then, the index of the customer satisfaction is introduced and its threshold is set to optimize the model. The genetic algorithm is designed to solve the optimized model. Finally, the efficiency of the model and the algorithm is verified with an example. The result shows that the optimized model can maximize the customer satisfaction with the lower distribution cost and the shorter distribution time. It is helpful for enterprises to improve the competitive advantage and satisfy the long-term interest without the risk of losing customers. customer satisfaction; logistics distribution; hard time window; soft time window; genetic algorithm 10.13340/j.jsmu.2015.03.011 1672-9498(2015)03-0064-07 2014-06-13 2014-09-29 国家自然科学基金(71171129);上海市自然科学基金(12PJ1404000) 赵锐(1989—),男,江苏淮安人,硕士研究生,研究方向为物流工程、物流资源配置和物流设备管理,(E-mail)ranenchao@gmail.com; 胡雄(1962—),男,上海人,教授,博导,博士,研究方向为港航物流装备的健康管理、故障诊断与安全评估, (E-mail)huxiong@shmtu.edu.cn F252.14;F252.2 A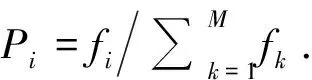
4 算例分析
5 结束语
