A review on logistics network design

HUANG Youfang, XU Dongmin, DING Yi,2, YANG Bin

(1. Academy of Science & Technology, Shanghai Maritime Univ., Shanghai 201306, China;2. Antai College of Economics & Management, Shanghai Jiaotong Univ., Shanghai 200240, China)



A review on logistics network design

HUANG Youfang1, XU Dongmin1, DING Yi1,2, YANG Bin1

(1. Academy of Science & Technology, Shanghai Maritime Univ., Shanghai 201306, China;2. Antai College of Economics & Management, Shanghai Jiaotong Univ., Shanghai 200240, China)

The decision-making support models for logistics network design are reviewed from four dimensions: (1) the complexity of modeling, including transportation period, product types and objective of modeling along with deterministic considerations, such as single or multiple product transport and single or multiple objective model; (2) modeling approaches and algorithms; (3) solution methods and technologies; (4) sustainability and robustness. It is identified that different considerations of complexity need a broader emphasis on emission and uncertainty during logistics network activities, that the sustainability is one of the major difficulties due to environmental and economic consideration, and that the robustness of more complex logistics networks is difficult to be tackled. CPLEX and LINGO are effective solvers for integer and/or bi-level programming models, but improved intelligent algorithms may be more feasible in practice for large-sized networks. Finally, the present and future practice-oriented research issues are recommended.

logistics network design; network complexity; sustainability; robustness

Biography：HUANG Youfang (1959-), male, born in Xinchang, Zhejiang province, professor, PhD supervisor, PhD, Research area is logistics system optimization, (E-mail)yhuang@shmtu.edu.cn

0 Introduction

Logistics activities has experienced a considerable expansion in the last two decades, during which many researchers paid attention to Logistics Network Design(LND), including forward/reverse LND and the solution method[1], robustness[2], system optimization[3]and carbon footprint regarding logistics network[4], etc. LND could trace back to MCDERMOTT[5]that discussed a particular industry and presented a simulation approach to LND. From 1970s to 1990s, there were relative less papers related to LND from systematic perspective. BALLOU[6]provided an overview of practical application of modeling to the business LND problem, and indicated two important dimensions of spatial and temporal. van der MEIJDENetal[7]presented an LND framework, which started with an analysis of external and internal developments and uncertainties. After 1990s, due to the activity requirements, both practitioners and academics were interested in LND in depth and in detail.

Actually LND comprises different decisions, while the basic objective of LND is aimed to keep flows smooth. Fig.1 illustrates a general LND problem including supply, production, distribution, etc. This paper reviews the articles pertaining to problem classification (including period, product and objective along with deterministic considerations), modeling, solution methods, decision and information technologies along with robustness and sustainability of logistics network, and presents ongoing and emerging issues.

Fig.1 A schematic diagram of general LND problem

1 Review methodology

This paper focuses on model-based literature and addresses LND issue. When reviewing these papers, related key words of LND limit these articles that describe LND incorporating urgent issues, solution to problem, integration degree and so on.

With this scope in mind, the search is conducted using library databases covering major journals in management science and applied science management, such asManagementScience,OperationsResearchTransportationScience,InternationalJournalofPhysicalDistribution&LogisticsManagement,InternationalJournalofLogisticsManagement,AdvancesinDistributionLogistics,ProductionandOperationsManagement,EuropeanJournalofOperationalResearch,Computers&IndustrialEngineering,InternationalJournalofInformationSystemsforLogisticsandManagement,TransportationResearchPartE:LogisticsandTransportationReview,TransportationResearchPartB:Methodological.

Eighty-two articles are retained among more than 100 articles, and all of which are clustered on a temporal basis; 4 of these articles were published before 2000, 5 in 2001-2005, 41 in 2006-2010, and 32 after 2010. In following problem classification, modeling and solution method, information technologies to solve problems will be discussed and analyzed.

2 Review and critiques of LND

2.1 Complexity of problem classification

FRIZELLEetal[8]proposed complexity from structural and operational perspectives. MEEPETCHDEEetal[9]developed complexity measurement based on degree of graph theory and expressed as degree of connectivity. In this paper, the complexity of LND covers a wide range of context, including operational and structural properties. Operational property encompasses period of logistics activity (Single-Period/SPr, Multi-Period/MPr), kind of product (Single-Product/SP, Multi-Product/MP), type of objective (Single-Objective/SO, Multi-Objective/MO), and timeliness of decision (Decision based on Dynamic Time/DDT, Decision based on Current Time/DCT), type of echelon (Single-Echelon/SE, Multi-Echelon/ME); structural property of logistics network contains capacity constraints (Uncapacitated Flow/UCF, Capacitated Flow/CF; Uncapacitated facility/UCa, Capacitated facaility/Ca), and properties of related parameters (Stochastic/Sto, Deterministic/Det).

Most early articles concentrated on SPr, SP, Det and uncapacitated constraint problems. MCDERMOTT[5]studied one-year period of operations on static view to minimize transportation cost and KRIKKEetal[10]researched reverse logistics network within one financial year and assumed no capacity limitation. CHEONGetal[11]considered two-echelon logistics network with differentiated delivery lead-time. CORDEAUetal[12]introduced a formulation with capacity constraints in deterministic demand, single period and single objective. MINetal[13]developed an ME product returning reverse logistics network to minimize total reverse logistics cost. VILAetal[14]discussed lumber industry logistics network with MP, ME facility locations and capacity options. LIECKENSetal[15]presented a recovery network with an SPr, SE and SP facility-location-allocation problem. LINetal[16]addressed a flexible multistage logistics network to minimize total cost, and the model considers single product, single time period, four echelons and deterministic demand. SALEMAetal[17]designed a capacitated MP reverse logistics network model with uncertainty on product demands and returns to minimize total cost. MINetal[18]proposed dynamic reverse logistics network considering various periods. SRIVASTAVA[19]formulated an MP, ME, profit maximizing reverse logistics network with different time periods.

About uncertainty of LND, more researchers focused on Sto factors. JEETetal[20]analyzed inventory stocking logistics network with low-demand parts following Possion distribution. LEEetal[21]extended a Det model of MPr reverse logistics network and proposed a two-stage Sto programming model with known distribution for demand/forward products. PISHVAEEetal[22]discussed integrated forward/reverse LND under uncertainty and proposed a Det model and an Sto model. QINetal[23]addressed multi-commodity logistics network with Sto demand and inventory control. EL-SAYEDetal[24]developed an MPr, ME forward-reverse logistics network with Sto demand. KARAetal[25]presented a two-stage Sto programming model for paper recycling reverse logistics network.

Most articles discussed cost minimization, and a few articles examined profit/revenue maximization[25-26]. CHESHMEHGAZetal[27]discussed MO problems (calculate the status open/close of suppliers, distribution centers or retailers; minimize delivery time, transportation cost and facility cost). HIREMATHetal[28]designed a four-echelon network with multiple objectives seeking for total cost minimization, unit fill rates and resource utilization of the facilities maximization. RAMEZANIetal[29]presented a stochastic MO (maximizing total profit, customer service level and increasing the Sigma quality) model for forward/reverse LND. ROGHANIANetal[30]employed an interactive fuzzy MO linear programming method to fuzzy bi-objective (minimize total cost and delivery time) reverse LND.

Although more than half of review articles addressed cost minimization and about a quarter addressed profit maximization, a few articles discussed response time minimization, reliability maximization, and resource utilization maximization. KRIKKEetal[10]addressed total operational cost minimization and reliability maximization. MINetal[18]minimized total logistics cost while maximizing cost saving. PISHVAEEetal[31]maximized responsiveness other than cost minimization in integrated logistics network. TUZKAYAetal[32]maximized the weighted product volume and minimized the cost. CHESHMEHGAZetal[33]and MIRAKHORLI[34]attached importance to customer response. KANNANetal[4]minimized cost, and cost component was extended to climate change, namely carbon emission cost. KANNANetal[4]and FROTA NETOetal[35]studied the Pareto efficiency in terms of cost and environment. These crucial review articles are generalized in Tab.1.

It is concluded that the variety and development of model objectives indicate focus change in real logistics network. Model objectives contain more diversified content from cost minimization or profit maximization to responsive time minimization, utilization rate maximization, robustness maximization, etc.

2.2 Modeling approaches and algorithms

Modeling contains continuous and discrete, and discrete models mainly include Mixed Integer Non-Linear Programming (MINLP), Mixed Integer Linear Programming (MILP) and Stochastic Mixed Integer Programming (SMIP) as well as Bi-Level Programming (BLP) models. Some articles established models Based on Scenario (BS) and approach. As for solution methods, a great number of articles applied intelligent algorithm to solve formulation as well as other mathematical methods. About a quarter of review articles laid emphasis on solution methods when dealing with the problem of LND.

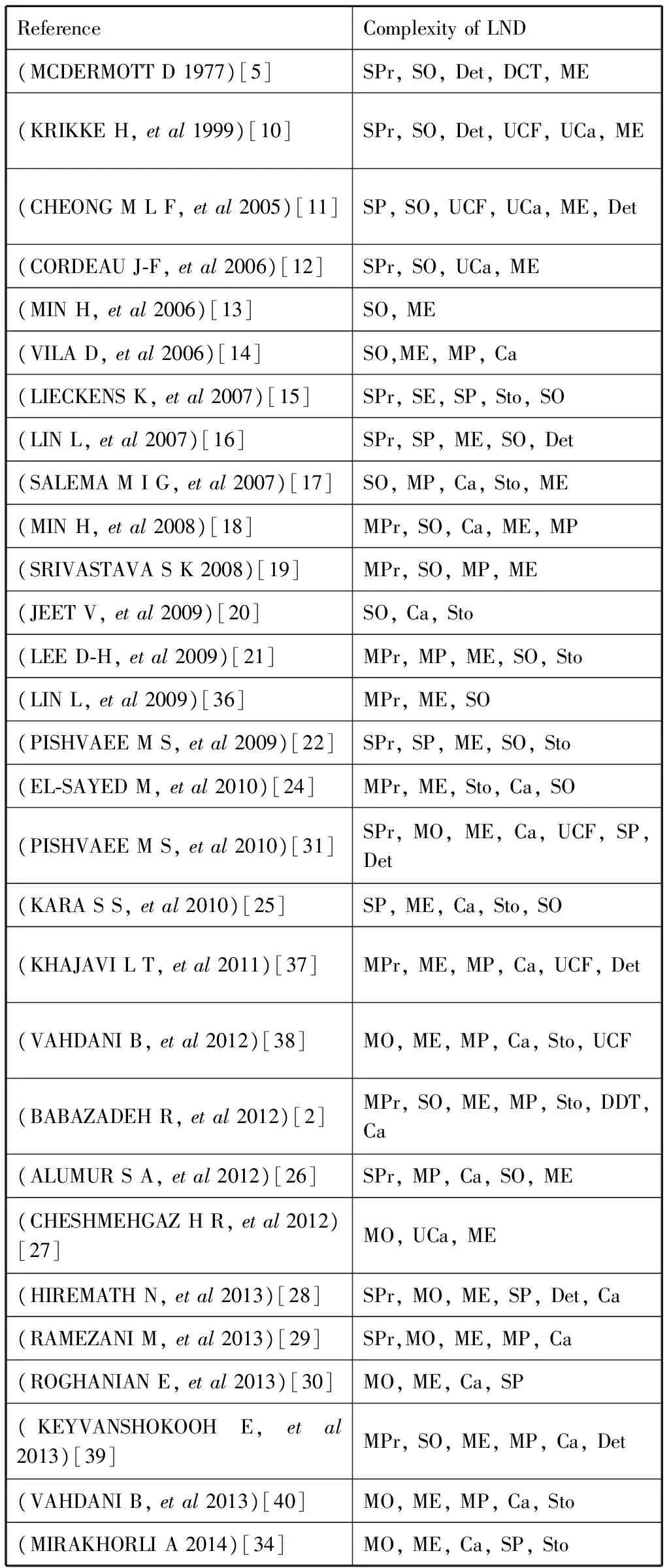
Tab.1 Partial review articles for problem classification of complexity

MINetal[13]proposed an MINLP model and designed a Genetic Algorithm (GA) to deal with it. LINetal[16]proposed a random path-based GA (rpGA) to solve a location-allocation problem. QINetal[41]designed a hybrid intelligent algorithm integrating fuzzy simulation and GA. HIREMATHetal[28]proposed an MILP model and employed a Non-dominated Sorting Genetic Algorithm-Ⅱ(NSGA-Ⅱ) to solve the model. LIECKENSetal[15]defined an MINLP model for Sto reverse logistics network, and a GA based on the Differential Evolution Algorithm (DEA) was used to solve the formulation.

MOSCATOetal[42]firstly defined a Memetic Algorithm (MA) to integrate local search in GA to improve search intensification. PISHVAEEetal[31]developed an MO MA to solve an MIP model. CORDEAUetal[12]described two approaches to locations and capacity choices, a simplex-based Branch-and-Bound Algorithm (BBA) and a Benders Decomposition Approach (BDA). LEEetal[43]developed a network flow-based Det programming model for end-of-lease computer products, and a Taboo Search (TS) was applied to determine the shipment of forward and returned products.

LINetal[36]extended the priority-based Evolutionary Algorithm (EA) to the hybrid Evolutionary Algorithm (hEA) combining local search with a new fuzzy logic control which enhanced the search ability of EA. CHESHMEHGAZetal[27]extended the guided Multi-Objective Evolutionary Algorithm (guided MOEA) and proposed a novel guided MOEA which is excellent in guiding evolutionary search without iterative and interactive process. CHESHMEHGAZetal[33]customized NSGA-Ⅱto find compromise solutions.

HEetal[44]designed a nonlinear integer planning model and developed a heuristic algorithm with nested Simulated Aunealing (SA). The Combined Simulated Annealing (CSA) algorithm is developed to deal with multi-level multi-commodity LND problems[23, 45]. PISHVAEEetal[46]proposed an MILP model in a multistage reverse logistics network, and SA algorithm with special neighborhood search mechanisms and the priority-based encoding method was applied to find the near optimal solution. THANHetal[47]presented a linear relaxation-based heuristic approach to solve MILP model, and the proposed LP-rounding performed successive Linear Relaxations (LR) and rounding steps until enough variables have been set at 0 or 1. THANHetal[48]defined a large scale MILP model, and a new heuristic method combining LR with the Difference of Convex functions Algorithm (DCA) was proposed to solve model.

LEEetal[21]explored a stochastic approach for dynamic reverse logistics network under uncertainty. A solution method integrating the Sample Average Algorithm (SAA) and SA algorithm was presented. LEEetal[49]further proposed a two-stage Sto programming model under uncertainty and developed SAA scheme with an importance sampling strategy to find the optimal solution.

VAHDANIetal[40]established an MILP formulation, and introduced the robust optimization approach, queuing theory and fuzzy MO programming to solve model. KIMetal[50]considered an integer programming model, and two heuristic algorithms, multi-stage BBA and the modified drop heuristics were suggested to deal with the problem. HARKSetal[51]formulated an MIP model, and proposed a fast Greedy Algorithm(fGA) and a Local Search Algorithm (LSA) to solve this model. CHIOU[3]proposed a BLP model, and a new Subgradient Projection Method (SPM) with global convergence was proposed. SUNetal[52]also proposed a BLP model with uncertain demand. The modeling approaches and algorithms of these review articles are listed in Tab.2.

Tab.2 Results of partial review articles for modeling and algorithms

2.3 Solution methodologies

KARAetal[25]mentioned used programs for logistics network models when outlining reverse logistics network. Actually different models may employ distinct programs depending on adaptability and other requirements. The used programs usually cover CPLEX, LINDO, LINGO, etc. In some conditions, the enumeration, such as the discrete grid enumeration was used to find solution.

FLEISCHMANNetal[53]mentioned a standard MILP solver which could attain all computational results. CORDEAUetal[12]employed CPLEX 6.6.1 with steepest-edge pricing, strong branching and a depth-first search to search integer solution. VILAetal[14]solved an MIP model with CPLEX 9.0, and found CPLEX setting adjustment may contribute to the reduction of computation time to some extent. Similarly, JEETetal[20]found that it could speed up computing to some extent without changing the model by adjusting some parameters/settings/options of the used program when solving MIP models. Besides, SRIVASTAVA[19], KEYVANSHOKOOHetal[39], WANGetal[54], and SOLEIMANIetal[55]solved an MILP model using CPLEX. LEEetal[21]solved a deterministic optimization problem by CPLEX 9.1.3. KARAetal[25]solved all Det, Sto models of MIP models by GAMS 21.6/CPLEX9.0. ALUMURetal[26]attained the optimal solution by CPLEX 11.2. SHUetal[56]solved the test instances by CPLEX 10.0. HARKSetal[51]tested the plain MIP formulations using CPLEX 12.1.

Some researchers compared CPLEX with other proposed solution methods. SALEMAetal[17]used GAMS/CPLEX 8.1 to solve an MILP model and found that the model size increases significantly and CPU time grows accordingly. CORDEAUetal[57]found that CPLEX is successful on small size models but fails to solve larger size models considering time consuming and solution quality. LEEetal[43]compared results of objective function values obtained from the proposed heuristic and estimated lower bounds obtained by CPLEX, and the results demonstrated that the former computational time is better than the latter when increasing the model size. GELAREHetal[58]found that the presented Lagrangian algorithm is at least one order of magnitude faster than CPLEX for finding solutions of similar quality. PENGetal[59]compared a hybrid meta-heuristic algorithm based on genetic algorithms and CPLEX, and found that the proposed meta-heuristic algorithm greatly outperforms CPLEX in terms of solution speed and solution quality. KIMetal[50]proposed a Multi-Stage Branch-and-Bound (MS-B&B) heuristic and a Modified Drop (M-DROP) heuristic for restricted dynamic models, and the results showed that CPLEX gives the optimal solution for small size instance, while CPLEX fails to attain the feasible solution when facing larger test instance beyond time limit. It can be found that some proposed methods or algorithms may be better than simply using extant solvers to find acceptable solutions according to aforementioned articles.

Another usually used solver is LINGO. MINetal[18]examined GA and BBA using LINGO, and found that the latter fails to produce feasible solutions even if more than one day is spent on it. PISHVAEEetal[31]compared non-dominated solutions of Multi-Objective Memetic Algorithm (MOMA) and LINGO. The results showed that the computation time for MOMA is significantly less than LINGO. MIRAKHORLI[34]found that LINGO cannot solve the problem with the increasing number of nodes, while a genetic-based heuristic algorithm is effective to solve the model for larger cases. It can be concluded that some proposed and designed algorithms show outperformance compared to solver of LINGO as abovementioned solver of CPLEX.

As LINGO, the other solver is LINDO. However, LINDO was seldom used compared to LINGO on account of parameter limit. Only CREAZZAetal[60]used LINDO 9.0 to solve the MILP model. There are several other specific solvers except for CPLEX, LINGO, LINDO, such as SITATION, MATLAB, Xpress-MP and IBM LogicNet Plus. CRUZ-RIVERAetal[61]used the facility location software SITATION to solve an objective model because SITATION can offer several solution methods for solving the Fixed Charge Facility Location Problem (FCFLP). HEetal[44]and ZHANGetal[62]solved MINLP and MIP models using MATLAB 7.0. PISHVAEEetal[46]coded SA in MATLAB 7.0 and compared the optimal solutions obtained by LINGO and SA algorithms. The results showed that SA algorithms spend much less time than LINGO. THANHetal[48]used the solver Xpress-MP (2007) to deal with the LP and MIP models. BINGetal[63]conducted an MIP reverse logistics network model by the graphical optimization tool IBM LogicNet Plus 7.1.

In summary, 38 articles relating to technique were reviewed, and about half of the articles referred to the used program. Most of the articles reviewed the solvers CPLEX and LINGO, and the minority of the articles solved the model by LINDO, MATLAB, etc. The conclusion is that the utilization of solvers not only relies on the property of the model, but also depends on the settings of solvers, and even other methods for solving the model are proposed and designed when the used solvers cannot perform.

2.4 An extension: sustainability and robustness analysis

Sustainability primarily stems from the concern and pressure of economy, environment, and government regulations. KRIKKE[64], MUTHAetal[65], ALUMURetal[26]concerned returned products and packages with Original Equipment Manufacturer (OEM). CRUZ-RIVERAetal[61], ZHOUetal[66], and BARKERetal[67]addressed reverse logistics network from sustainability perspective. FLEISCHMANNetal[53]analyzed electronics industry reverse logistics flows. Similarly, LEEetal[43]focused on the take-back for electronic products on account of environmental legislation.

An increasing number of articles focused on product recovery and recycle. KARAetal[25]studied paper reverse LND. LEEetal[49]indicated forward product flow and reverse product flow. SASIKUMARetal[1]stated the trend of recovery processes of end-of-life products and that of recycling due to increasing environmental deterioration, government regulations, social responsibilities and economic factors. de ROSAetal[68]stated that reverse logistics networks are significant to improve company sustainability footprint and proposed the joint integration logistics network with bi-directional product flows.

Reverse logistics emergency primarily booted in the sustainability of LND, whilst reverse LND varies in terms of returned products in practice. DASetal[69]discussed an integrated, reverse logistics supply chain planning process with modular product design. BINGetal[63]discussed the sustainable reverse LND for household plastic waste in Netherlands.

Besides the sustainability of LND itself, some researchers studied in further, including how to evaluate sustainable logistics network. FROTA NETOetal[35]shed light on the design of logistics networks balancing profit and environment. Eco-efficiency is set as a criterion of sustainable logistics network and data envelopment analysis is employed to assess Pareto efficiency of sustainability for logistics network.

Robustness is often considered from the beginning of LND. Robustness means the resilience after facility failure and adjustment capacity due to uncertain factors such as stochastic demand/supply, returned products, variant time, etc. MEEPETCHDEEetal[9]studied the relationship between the robustness of logistics network and the topological property of logistics network. MEEPETCHDEEetal[9]considered the robustness of the logistics network depending on the ability of each vertex to communicate or interact, directly or indirectly, with all other vertices in the network. PENGetal[59]shed light on reliable LND with facility disruptions. PENGetal[59]carefully planned for disruption scenarios that may develop new design, and the design added the backup facility to cope with facility disruption. BERTSIMASetal[70]considered network uncertainty of network structure (e.g., nodes and arcs) with known and deterministic parameters, and presented an adaptive two-stage model which may adjust the solution flexibly after the realization of the failures in the network compared to the robust model.

While in a given logistics network, the robustness of logistics network may derive from stochasticity/uncertainty in logistics activity, and these stochastic/uncertain factors may be the stochastic demand/supply, returned products, variant time, etc. The robustness can be considered by decision adjustment during operational process instead of LND from scratch. Meanwhile, reverse logistics leads to robustness problems, which increases the difficulties for determining the capacity and location decisions. Therefore, it is necessary to reckon volatile demand and supply as key drivers for concluding capacity adjustment and site location plans[49]. de ROSAetal[68]introduced a detailed deterministic model to assess the impact of incorporating reverse logistics into a forward-oriented supply chain. VAHDANIetal[40]gave a deeper analysis for reliability of logistics network facing the uncertainties.

From these articles aforementioned, it is concluded that the sustainability of LND shows economic and environmental coincidence. The robustness/reliability covers two aspects: (1) design consideration in advance; (2) decision consideration in operation. The former pays attention to logistics network configuration; the latter lays emphasis on decision making in extant logistics network. Both design consideration and decision consideration make logistics activity more strong robust.

3 Discussion

Complexity has a broad understanding of context including period of logistics activity, kind of product, type of objective, and timeliness of decisions as well as network capacity constraints. Tab.1 illustrates these articles about complexity of LND in chorological order. It can be seen that before 2005 most of existing models considered single period, single product, single objective, deterministic parameters and incapacity, and there was a complicated trend after 2005. The models of multi-periods, multi-products, multi-objectives, stochastic and capacity limitation emerged. These show that the models inclined to more practical and specified, especially stochastic considerations. After 2005, 11 articles dealt with stochastic parameters. Dynamic decision models of LND were addressed until 2012, when BABAZADEHetal[2]considered a real-world integrated logistics network and provided a proper platform based on dynamic time, which is applicable for decision in real time. In addition, most models addressed cost minimization or profit maximization. The findings show more researchers/companies lay much emphasis on economic benefit. A few articles seek for customer responsiveness time minimization, robustness maximization, and carbon emission minimization with development. The lack of attention is likely due to benefit requirements for operator. Although it is crucial to keep cost-effective and effective customer responsiveness, more attention should be given on environmental and robust considerations, because carbon emission may be seen as one kind of cost and destructive force in future after failures and uncertainty occurrences becoming much greater due to more complex logistics network activity and structure.

As for modeling and algorithms, the models usually covers MINLP, MILP, SMIP and BLP models, whilst some articles established some models based on scenario and approach. A great number of articles applied intelligent algorithms to solve formulation as well as other mathematical methods including GA, EA, SA, TS, etc. Tab.2 summarizes the findings concerning modeling and algorithms, and it is evident that intelligent algorithms dominate the list. Modeling has direct influence on algorithms, and non-linearity and mixed integer in objective function cause more difficulties to solve. Most algorithms are based on GA and EA, but the problem of mixed integer linear has broader algorithms. CHIOU[3]and SUNetal[52]formulated a BLP model, which is beneficial to optimize global system and feasible for management decision. Compared to MILP, BLP gives more directions in strategic and operational level which is available in real-world logistics network. While BLP, mainly non-linear BLP, faces difficulties in algorithm, developing an effective algorithm for BLP is meaningful and important. Note from Tab.2 that most of models are mixed-integer, which shows that most logistics network models deal with facility location by the binary variable 0 and 1.

It is clear that distinct models may use various programs considering the adaptability of some programs and other requirements and limit. According to above analysis, the majority of review articles use CPLEX and LINGO, and the minority of those use MATLAB, Xpress, SITATION and IBM LogicNet Plus. CPLEX is an effective solver for integer programming. However, it is not accessible to feasible solution due to time limitation when dealing with large instance. By analyzing the computational results, SALEMAetal[17]found that the model size increases significantly and the CPU time grows accordingly, and PENGetal[59]noticed that the meta-heuristic algorithm greatly outperforms CPLEX in terms of solution speed and solution quality. Therefore, it is crucial to develop and present effective algorithms. Similarly, MIRAKHORLI[34]found that LINGO cannot find feasible solution with the increasing number of nodes, and presented a genetic-based heuristic algorithm to solve the model for larger cases. It is critical to attain feasible solution for real-world logistics with time limitation, and it is necessary to design and propose other method when the used solver cannot perform within constraints due to logistics expansion. In addition, it may be an attempt to transfer different solvers. PISHVAEEetal[46]compared the optimal solutions obtained by LINGO with SA in MATLAB, and the results show that SA spends much less time than LINGO. Improved algorithms and corresponding solvers will be effective and efficient to attain optimal/feasible solution within time limitation and size expansion.

Sustainability originated from environmental consideration and government regulations/legislations as well as economic benefits, which contributes to the attention of reverse logistics, including used products, recyclable and returned goods, waste disposal. KRIKKE[64], ALUMURetal[26], and MUTHAetal[65]discussed that OEMs is responsible for taking back their used, end-of-lease or end-of-life products. LEEetal[43], FLEISCHMANNetal[53], KARAetal[25]examined the take-back for electric products and paper reverse logistics respectively, but the range and coverage of incustries for sustainability explored appears to be limited. However, FROTA NETOetal[35]proposed eco-efficiency as sustainable criterion. From both perspectives of operators and governors, the sustainability of logstics network may attain balance between cost-efficiency and eco-efficiency.

The robustness of logistics network involves two aspects. One is topological property robustness when designing logistics network, which expects the probability of future logistic activity; the other is implementation robustness during operational process in a given logistics network, and the robustness can be considered by decision adjustment during operational process instead of LND from scratch. MEEPETCHDEEetal[9]considered the robustness of the logistics network depending on the ability of each vertex to communicate or interact, directly or indirectly, with all other vertices in the network; PENGetal[59]and BERTSIMASetal[70]gave more attention on operational robustness, namely the adjustment and coordination after disruptions and failures. In addition, reverse logistics activities may easily lead to robustness problem due to its uncertainty, and VAHDANIetal[38]and de ROSAetal[68]gave a much deeper analysis of robustness for reverse logistics. Although general models presented these aspects of robustness for logistics network, industry-based models are lack. A need for industry-based models should be provided in future research.

4 Conclusion

This paper reviews the model-based literature for the LND, and examines the complexity of models, modeling and algorithms, solution methods, sustainability and robustness. Overall, it is found that although researchers have tackled some complicated logistics network, few models compressively address the problems of emission, uncertainty accompanied by complexity, and difficulties of modeling and solution.

First, it is concluded that LND need extend the complexity of models and pay attention to emerging emission issues along with stochastic problems. Spatial and temporal coordinations will be more important for environment and benefit, and new measurements for coordination are necessary. The objective of modeling should be extended to carbon emission, energy consumption, responsiveness time as well as cost and profit due to increasing attention paid to the environment and energy. More and more uncertainty will arise due to extension of the complexity.

Secondly, the MIP model is the main model for facility location, which gives effective decision assistance, while the BLP model is more practical for the strategic and operational from overall considerations. Non-linearity for models is ordinary within objective and constraints, which requires improved algorithms. Intelligent algorithms will be effective and efficient for logistics network models. In addition, the selection of solvers has closely relationship with different models. CPLEX is suitable for integer planning; however, it fails to attain feasible solutions in some large instances, and improved intelligent algorithms may find feasible solutions within time and storage limitation. The development of intelligent algorithms is necessary for complicated logistics network. Besides, decision and information technologies enlighten us that the setting of solvers may help in decrease of time spending and storage space, and it is essential to propose new method to improve performance facing failure of the solvers.

Thirdly, sustainability and robustness will be two major difficulties in logistics network. Sustainability is closely related with environmental consideration which is inevitable for operators due to that legislation, and the original LND and successive operation should balance economy and ecology. Robustness needs to be considered from scratch once designing network, and topological property of logistics network will impact on robustness in future; the research of coordination and resilience will be meaningful when dealing with disruptions and uncertainty in a given logistics network. More industry-based models need to be investigated in the context of sustainability for LND. A number of industries have been explored in the model-based literature, including electronic and paper recycle; other industries have not been investigated with emerging issues. The challenge for any particular industry is to strategically decide on those features that will be modeled, therefore model development towards focusing on the special structure of practical setting will be important in practice.

[1]SASIKUMAR P, KANNAN G, HAQ A N. A multi-echelon reverse logistics network design for product recovery - a case of truck tire remanufacturing[J]. Int J Adv Manufacturing Technol, 2010, 49(9-12): 1223-1234.

[2]BABAZADEH R, TAVAKKOLI-MOGHADDAM R, RAZMI J. A complex design of the integrated forward-reverse logistics network under uncertainty[J]. Int J Ind Eng, 2012, 23(2): 113-23.

[3]CHIOU S W. A bi-level programming for logistics network design with system-optimized flows[J]. Inform Sci, 2009, 179(14): 2434-2441.

[4]KANNAN D, DIABAT A, ALREFAEI M,etal. A carbon footprint based reverse logistics network design model[J]. Resources, Conservation & Recycling, 2012, 67: 75-79.

[5]MCDERMOTT D. Logistics network design: a simulation study of a nursery stock channel[J]. Int J Phys Distribution & Logistics Manage, 1977, 8(2): 62-73.

[6]BALLOU R H. Logistics network design: modeling and informational considerations[J]. Int J Logistics Manage, 1995, 6(2): 39-54.

[7]van der MEIJDEN L H, van NUNEN J A. Strategic decision making for logistics network design[J]. Adv Distribution Logistics, 1998，460: 83-109.

[8]FRIZELLE G, WOODCOCK E. Measuring complexity as an aid to developing operational strategy[J]. Int J Operations & Production Manage, 1995, 15(5): 26-39.

[9]MEEPETCHDEE Y, SHAH N. Logistical network design with robustness and complexity considerations[J]. Int J Physical Distribution & Logistics Manage, 2007, 37(3): 201-222.

[10]KRIKKE H, van HARTEN A, SCHUUR P. Business case Oce: reverse logistic network re-design for copiers[J]. OR-Spektrum, 1999, 21(3): 381-409.

[11]CHEONG M L F, BHATNAGAR R, GRAVES S C. Logistics network design with differentiated delivery lead-time: benefits and insights[J]. working paper, 2005.

[12]CORDEAU J-F, PASIN F, SOLOMON M M. An integrated model for logistics network design[J]. Annals of Operations Research, 2006, 144(1): 59-82.

[13]MIN H, JEUNG K H, SEONG K C. A genetic algorithm approach to developing the multi-echelon reverse logistics network for product returns[J]. Omega, 2006, 34(1): 56-69.

[14]VILA D, MARTEL A, BEAUREGARD R. Designing logistics networks in divergent process industries: a methodology and its application to the lumber industry[J]. Int J Production Econ, 2006, 102(2): 358-378.

[15]LIECKENS K, VANDAELE N. Reverse logistics network design with stochastic lead times[J]. Computers & Operations Res, 2007, 34(2): 395-416.

[16]LIN L, GEN M, WANG X. A hybrid genetic algorithm for logistics network design with flexible multistage model[J]. Int J Inform Systems Logistics & Manage, 2007, 3(1): 1-12.

[17]SALEMA M I G, BARBOSA-POVOA A P, NOVAIS A Q. An optimization model for the design of a capacitated multi-product reverse logistics network with uncertainty[J]. Eur J Operational Res, 2007, 179(3): 1063-1077.

[18]MIN H, KO H-J. The dynamic design of a reverse logistics network from the perspective of third-party logistics service providers[J]. Int J Production Econ, 2008, 113(1): 176-192.

[19]SRIVASTAVA S K. Network design for reverse logistics[J]. Omega, 2008, 36(4): 535-548.

[20]JEET V, KUTANOGLU E, PARTANI A. Logistics network design with inventory stocking for low-demand parts: modeling and optimization[J]. IIE Trans, 2009, 41(5): 389-407.

[21]LEE D-H, DONG M. Dynamic network design for reverse logistics operations under uncertainty[J]. Transportation Res Part E: Logistics & Transportation Rev, 2009, 45(1): 61-71.

[22]PISHVAEE M S, JOLAI F, RAZMI J. A stochastic optimization model for integrated forward/reverse logistics network design[J]. J Manufacturing Systems, 2009, 28(4): 107-114.

[23]QIN J, SHI F, MIAO L-X,etal. Optimal model and algorithm for multi-commodity logistics network design considering stochastic demand and inventory control[J]. Systems Eng Theory & Practice, 2009, 29(4): 176-83.

[24]EL-SAYED M, AFIA N, EL-KHARBOTLY A. A stochastic model for forward-reverse logistics network design under risk[J]. Computers & Ind Eng, 2010, 58(3): 423-431.

[25]KARA S S, ONUT S. A stochastic optimization approach for paper recycling reverse logistics network design under uncertainty[J]. Int J Environ Sci & Technol, 2010, 7(4): 717-730.

[26]ALUMUR S A, NICKEL S, SALDANHA-DA-GAMA F,etal. Multi-period reverse logistics network design[J]. Eur J Operational Res, 2012, 220(1): 67-78.

[27]CHESHMEHGAZ H R, ISLAM M N, DESA M I. A polar-based guided multi-objective evolutionary algorithm to search for optimal solutions interested by decision-makers in a logistics network design problem[J]. J Intelligent Manufacturing, 2012, 25(4): 699-726.

[28]HIREMATH N, SAHU S, TIWARI M K. Multi-objective outbound logistics network design for a manufacturing supply chain[J]. J Intelligent Manufacturing, 2013, 24(6): 1071-1084.

[29]RAMEZANI M, BASHIRI M, TAVAKKOLI-MOGHADDAM R. A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level[J]. Appl Math Modelling, 2013, 37(1): 328-344.

[30]ROGHANIAN E, KAMANDANIPOUR K. A fuzzy-random programming for integrated closed-loop logistics network design by using priority-based genetic algorithm[J]. Int J Ind Eng Computations, 2013, 4(1): 139-154.

[31]PISHVAEE M S, FARAHANI R Z, DULLAERT W. A memetic algorithm for bi-objective integrated forward/reverse logistics network design[J]. Computers & Operations Res, 2010, 37(6): 1100-1112.

[32]TUZKAYA G, GÜLSÜN B, ÖNSEL ξ. A methodology for the strategic design of reverse logistics networks and its application in the Turkish white goods industry[J]. Int J Production Res, 2011, 49(15): 4543-4571.

[33]CHESHMEHGAZ H R, DESA M I, WIBOWO A. A flexible three-level logistic network design considering cost and time criteria with a multi-objective evolutionary algorithm[J]. J Intelligent Manufacturing, 2013, 24(2): 277-293.

[34]MIRAKHORLI A. Fuzzy multi-objective optimization for closed loop logistics network design in bread-producing industries[J]. Int J Adv Manufacturing Technol, 2014, 70(1-4): 349-362.

[35]FROTA NETO J Q, BLOEMHOF-RUWAARD J M, van NUNEN J,etal. Designing and evaluating sustainable logistics networks[J]. Int J Production Econ, 2008, 111(2): 195-208.

[36]LIN L, GEN M, WANG X. Integrated multistage logistics network design by using hybrid evolutionary algorithm[J]. Computers & Ind Eng, 2009, 56(3): 854-73.

[37]KHAJAVI L T, SEYED-HOSSENI S M, MAKUI A. A mathematical model for optimization of an integrated network logistics design[J]. Manage Sci Lett, 2011, 1(4): 415-426.

[38]VAHDANI B, TAVAKKOLI-MOGHADDAM R, MODARRES M,etal. Reliable design of a forward/reverse logistics network under uncertainty: a robust-M/M/c queuing model[J]. Transportation Res Part E: Logistics & Transportation Rev, 2012, 48(6): 1152-1168.

[39]KEYVANSHOKOOH E, FATTAHI M, SEYED-HOSSEINI S,etal. A dynamic pricing approach for returned products in integrated forward/reverse logistics network design[J]. Appl Math Modelling, 2013, 37(24): 10182-10202.

[40]VAHDANI B, TAVAKKOLI-MOGHADDAM R, JOLAI F. Reliable design of a logistics network under uncertainty: a fuzzy possibilistic-queuing model[J]. Appl Math Modelling, 2013, 37(5): 3254-3268.

[41]QIN Z, JI X. Logistics network design for product recovery in fuzzy environment[J]. Eurn J Operational Res, 2010, 202(2): 479-490.

[42]MOSCATO P, NORMAN M G. A memetic approach for the traveling salesman problem implementation of a computational ecology for combinatorial optimization on message-passing systems[J]. Parallel Computing & Transputer Applications,1992, 1: 177-186.

[43]LEE D-H, DONG M. A heuristic approach to logistics network design for end-of-lease computer products recovery[J]. Transportation Res Part E: Logistics & Transportation Rev, 2008, 44(3): 455-474.

[44]HE B, MENG W-D. A heuristic approach to reverse logistics network design for product return[J]. Operations Res & Manage Sci, 2010, 19(1): 73-79.

[45]QIN Jin, NI Linglin, MIAO Lixin. Optimization model and combined simulated annealing algorithm for multi-level multi-commodity logistics network design[J]. Application Res Computers, 2010, 27(9): 3348-3351.

[46]PISHVAEE M S, KIANFAR K, KARIMI B. Reverse logistics network design using simulated annealing[J]. Int J Adv Manufacturing Technol, 2010, 47: 269-281.

[47]THANH P N, PéTON O, BOSTEL N. A linear relaxation-based heuristic approach for logistics network design[J]. Computers & Ind Eng, 2010, 59(4): 964-975.

[48]THANH P N, BOSTEL N, PÉTON O. A DC programming heuristic applied to the logistics network design problem[J]. Int J Production Econ, 2012, 135(1): 94-105.

[49]LEE Der-Horng, DONG Meng, BIAN Wen. The design of sustainable logistics network under uncertainty[J]. Int J Production Econ, 2010, 128(1):159-166.

[50]KIM J S, LEE D H. A restricted dynamic model for refuse collection network design in reverse logistics[J]. Computers & Ind Eng, 2013, 66(4): 1131-1137.

[51] HARKS T, KONIG F G, MATUSCHKE J,etal. An integrated approach to tactical transportation planning in logistics networks[J]. Transportation Sci, 2014: 1-22. http://dx.doi.org/10.1287/trsc.2014.0541.

[52]SUN Q, WANG Q, GAO Y L. Multi-period bi-level programming model for regional comprehensive transport network design with uncertain demand[J]. J Transportation Systems Eng & Inform Technol, 2011, 11(6): 111-116.

[53]FLEISCHMANN M, BLOEMHOF-RUWAARD J M, BEULLENS P,etal. Reverse logistics network design[J]. Reverse Logistics, 2004: 65-94.

[54]WANG S, MENG Q. Reversing port rotation directions in a container liner shipping network[J]. Transportation Res Part B: Methodological, 2013, 50: 61-73.

[55]SOLEIMANI H, GOVINDAN K. Reverse logistics network design and planning utilizing conditional value at risk[J]. Eur J Operational Res, 2014, 237(2): 487-497.

[56]SHU J, LI Z, SHEN H,etal. A logistics network design model with vendor managed inventory[J]. Int J Production Econ, 2012, 135(2): 754-761.

[57]CORDEAU J-F, LAPORTE G, PASIN F. An iterated local search heuristic for the logistics network design problem with single assignment[J]. Int J Production Econ, 2008, 113(2): 626-640.

[58]GELAREH S, NICKEL S, PISINGER D. Liner shipping hub network design in a competitive environment[J]. Transportation Res Part E: Logistics & Transportation Rev, 2010, 46(6): 991-1004.

[59]PENG P, SNYDER L V, LIM A,etal. Reliable logistics networks design with facility disruptions[J]. Transportation Res Part B: Methodological, 2011, 45(8): 1190-1211.

[60]CREAZZA A, DALLARI F, ROSSI T. Applying an integrated logistics network design and optimisation model: the Pirelli Tyre Case[J]. Int J Production Res, 2012, 50(11): 3021-38.

[61]CRUZ-RIVERA R, ERTEL J. Reverse logistics network design for the collection of end-of-life vehicles in Mexico[J]. Eur J Operational Res, 2009, 196(3): 930-939.

[62]ZHANG W, XU D. Integrating the logistics network design with order quantity determination under uncertain customer demands[J]. Expert Systems with Applications, 2014, 41(1): 168-175.

[63]BING X, BLOEMHOF-RUWAARD J M, van der VORST J G. Sustainable reverse logistics network design for household plastic waste[J]. Flexible Services & Manufacturing J, 2014, 26(1/2): 119-142.

[64] KRIKKE H. Recovery strategies and reverse logistics network design[J]. Greener Manufacturing & Operations from Design to Delivery & Back, 2001(17): 256-272.

[65]MUTHA A, POKHAREL S. Strategic network design for reverse logistics and remanufacturing using new and old product modules[J]. Computers & Ind Eng, 2009, 56(1): 334-346.

[66]ZHOU Y, WANG S. Genetic model of reverse logistics network design[J]. J Transportation Systems Engineering & Inform Technol, 2008, 8(3): 71-78.

[67]BARKER T J, ZABINSKY Z B. Reverse logistics network design: a conceptual framework for decision making[J]. Int J Sustainable Eng, 2008, 1(4): 250-260.

[68]de ROSA V, GEBHARD M, HARTMANN E,etal. Robust sustainable bi-directional logistics network design under uncertainty[J]. Int J Production Econ, 2013, 145(1): 184-198.

[69]DAS K, CHOWDHURY A H. Designing a reverse logistics network for optimal collection, recovery and quality-based product-mix planning[J]. Int J Production Econ, 2012, 135(1): 209-221.

[70]BERTSIMAS D, NASRABADI E, STILLER S. Robust and adaptive network flows[J]. Oper Res, 2013, 61(5): 1218-1242.

(Editor JIA Qunping)

物流网络设计综述

黄有方1， 许冬敏1， 丁一1,2， 杨斌1

(1. 上海海事大学 科学研究院，上海 201306；2. 上海交通大学 安泰经济管理学院，上海 200240)

从四方面评述物流网络设计决策支持模型：(1)建模复杂性，包括运输时期、产品类型、模型目标以及确定性考虑，如单一产品或多产品运输，单目标模型或多目标模型；(2)建模方法与算法；(3)求解方法与技术；(4)持续性与鲁棒性.分析发现复杂性考虑需要更加注重物流网络活动排放和不确定性，环境和经济考虑使持续性成为物流网络设计主要困难之一，难以处理更加复杂物流网络的鲁棒性问题.CPLEX和LINGO通常能有效求解整数和/或双层规划模型，但对于大规模物流网络而言，改进的智能算法在实际求解中更为可行.最后提出目前和未来以实践为研究方向的有关问题.

物流网络设计； 网络复杂性； 持续性； 鲁棒性

10.13340/j.jsmu.2015.03.009

1672-9498(2015)03-0046-11

F250 Document code： A

s：the National Natural Science Foundation of China (71171129, 71301101); the Specialized Research Fund for the Doctoral Program of Higher Education of China (20123121110004)

Received date：2014-08-02 Revised date：2015-04-02