改进的正反馈主动频移式孤岛检测方法

黎璋霞，罗晓曙，廖志贤，陈亚欢

（广西师范大学电子工程学院，桂林541004）

改进的正反馈主动频移式孤岛检测方法

黎璋霞，罗晓曙，廖志贤，陈亚欢

（广西师范大学电子工程学院，桂林541004）

孤岛效应是光伏并网逆变器发电系统中存在的一个基本问题。对孤岛效应的检测必须准确而快速，同时孤岛检测的方法应该尽量减小对电能质量的影响。该文阐述了主动频移AFD（active frequency drift）检测法和正反馈主动频移AFDPF（active frequency driftwith positive feedback）检测法的基本原理、分析了AFDPF的检测盲区，并在此基础上提出一种改进的AFDPF检测法，即以分段函数的方式施加扰动来达到频移的方法。最后在Matlab/Simulink平台进行仿真实验，验证了该改进的AFDPF检测法不仅具有可行性，而且降低了电流谐波失真度THD（total harmonic distortion），即减小了扰动对电能质量的影响。

光伏并网逆变器；孤岛检测；正反馈主动频率偏移检测；检测盲区；谐波失真度

随着越来越多的光伏并网逆变器加入到公共主电网中，使得孤岛效应这个问题日益突出。孤岛效应[1]是指当电力公司因电路故障或停电维修等原因停止供电时，用户端的并网逆变器仍处于工作状态，使并网逆变器和周围的负载形成一个电力公司无法控制的自供电网络。当并网发电系统发生孤岛效应时，若不能及时检测到孤岛并停止逆变器的运行，将可能对用电设备带来损害以及对维修人员造成伤害。因此，准确而可靠的孤岛检测方法是光伏并网发电系统实现反孤岛功能的前提。

主动频移AFD（active frequency drift）孤岛检测法是一种较好的孤岛检测方法，其检测效率较高，同时不需要加入任何硬件设备，所以国内外很多学者对该方法进行了深入研究并取得了显著成果。

文献[2]通过理论分析和数值模拟推导出了正反馈主动频移AFDPF（active frequency drift with positive feedback）孤岛检测方法中反馈增益的取值范围；文献[3]研究了基于品质因数Qf0为横坐标，电容归一化值Cnorm为纵坐标的坐标系法下的检测盲区，分析了孤岛检测盲区的相应表达式。这些研究成果对孤岛检测的应用具有较好的理论指导意义。

本文在前人研究的基础上，通过对正反馈主动频率偏移孤岛检测法中的截断系数cf的表达式进行研究，针对AFDPF孤岛检测法在检测盲区和谐波畸变率上的不足，对该检测方法进行改进，从而在兼顾检测速度和总谐波失真度的基础上进一步减小了孤岛检测盲区。最后通过仿真验证了该改进方法的有效性。

1 AFDPF的工作原理

1.1 AFDPF的检测原理

主动频率偏移孤岛检测方法的思想[4-5]是：控制光伏并网逆变器发电系统输出电流的给定频率，使电流频率比上一周期电网和并网逆变器的公共连接点PCC（the pointof common coupling）电压的频率略高（或略低），即若电流半波已完成而电压未到过零点，则强制电流给定为零，直到电压过零，电流才开始下一个半波[6]，如图1所示。

图1 光伏并网逆变器输出电流的参考信号Fig.1 Reference signalof the PV grid-connected inverter output current

当主电网断电后，若不能及时停止逆变器，将会使PCC点的电压频率不断增加，直到满足相角判据

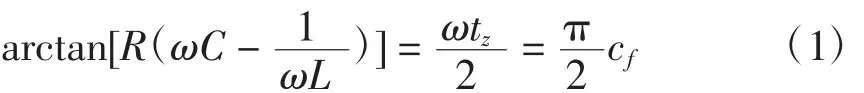
式中：R、L、C分别为负载电路的电阻、电感和电容值；ω为公共点电压的角频率；tz为电流过零点超前或滞后电压过零点的时间间隔为截断系数（chopping fraction），其中T为公共点电压的周期。

针对传统的AFD检测法中检测盲区较大的不足，AFDPF检测法在主动频移法的基础上加入了线性正反馈的部分[6]，即电流的截断系数

式中：cf0为初始截断系数；k为反馈增益；由于主电网断电后，公共点电压的频率受电流频率的影响而偏离原值，定义Δf=f-f0为公共点电压频率f与主电网电压频率f0之差（这里f0=50Hz）。

1.2 AFDPF检测法的检测盲区

检测盲区NDZ（non-detection zone），即孤岛检测失效的负载范围，通常用检测盲区来判断孤岛检测的有效性。由于以品质因数Qf0为横坐标，电容归一化值Cnorm为纵坐标的坐标系法使用范围广，能够清楚直观地反映负载对孤岛检测盲区的影响[3]，所以在本文的研究中采用该方法对AFDPF的检测盲区进行分析。

首先定义关系式

式中：ω0为主电网电压角频率；L、C分别为负载电感和电容值；Qf0为品质因数；Cres为负载的谐振电容值为电容的归一化值。结合式（1）的相角判据，将ω=ω0+Δω，cf=cf0+kΔf，C=CnormCres=（1+ΔC）Cres代入相角判据得

按国家标准，主电网的额定频率f0=50 Hz，当|Δf|>0.5Hz时继电器动作，切断并网逆变器的供电。将式（6）化简后并将Δf的上下限0.5Hz和-0.5Hz代入式（6）得

上式即为检测盲区的归一化电容值范围。由式（7）可以得到如图2所示的NDZ分布图。

图2 AFDPF检测法在不同取值下的NDZ分布图Fig.2 NDZ distribution for AFDPFmethod under differentvalues

在图2中，图（a）的左、中、右分别为cf= 0.02Δf、cf=0.05Δf、cf=0.10Δf，即cf0=0；图（b）的左、中、右分别为cf=0.01+0.02Δf、cf=0.01+ 0.05Δf、cf=0.01+0.10Δf，即cf0=0.01。比较图（a）和图（b）可得，增大初始截断系数cf0只会使检测盲区上移，并不会影响检测盲区的大小。同时，随着反馈系数k的增大，检测盲区的范围向右移动到品质因数更高的范围，能够在Qf0＜2.5的条件下实现孤岛检测无盲区。

2 具有线性、非线性以及饱和限幅特性的截断系数cf的选取

在AFDPF检测法中，增大反馈增益能有效地减少检测盲区。但是，k的不断增大使电能质量受损并破坏系统的稳定，所以k不是越大越好。IEEE Std.2000-929规定负载品质因数为2.5，即对品质因数小于等于2.5的所有负载，若能实现孤岛检测无盲区即满足要求[2]。综上所述，为了在减小谐波失真度和减小检测盲区中折中考虑，并充分考虑电网频率在50±0.2 Hz范围内的正常变化情况，防止孤岛保护误动作，尽量减少所施加的频率干扰对电能质量的不良影响[7]，本文设定AFDPF算法中的cf=f（Δf）为具有线性、非线性以及饱和限幅特性的分段函数。

在本文的方法中，首先在检测算法中引入一个关键变量n，n表示0.2 s内公共耦合点电压频率朝大于50Hz或小于50Hz变化的次数，并通过n的取值范围决定加入到系统中的扰动cf的函数f（Δf）的表达式为

定义n的初值为0，若PCC点电压的频率大于50 Hz或者小于50Hz，n都自动增1。

式（8）中：当变化次数不超过3次时，考虑电网正常时允许的电压频率波动范围为±0.2Hz，则cf=cf0+kΔf3，当Δf=0.1时，Δf3=0.001，此时施加的扰动则很小，保证在非孤岛状态下对电能质量的影响最小；当n超过3次时，加强频率干扰，加速频率越限，从而检测出孤岛；当n超过10次时，说明主电网已经发生故障，若此时频率仍未越限，则给输入最大扰动（该最大扰动的允许值0.046和-0.045由文献[8]中的THD与截断系数关系曲线得到），迅速停止逆变器运行。

3 仿真与验证

为了验证参数的有效性，结合上述AFDPF孤岛检测算法，在Matlab/Simulink平台上对该算法进行仿真。选取的RLC组合的参数为R=6.01Ω，L=7.65×10-3H，C=1.3×10-3F，Qf=2.5，谐振频率为50Hz。

本文设定cf0=0.01，k=0.1，对传统的AFDPF和改进的AFDPF检测法进行仿真比较，仿真设定主电网在0.06 s时刻断开。算法流程如图3所示，仿真结果如图4~图6所示。

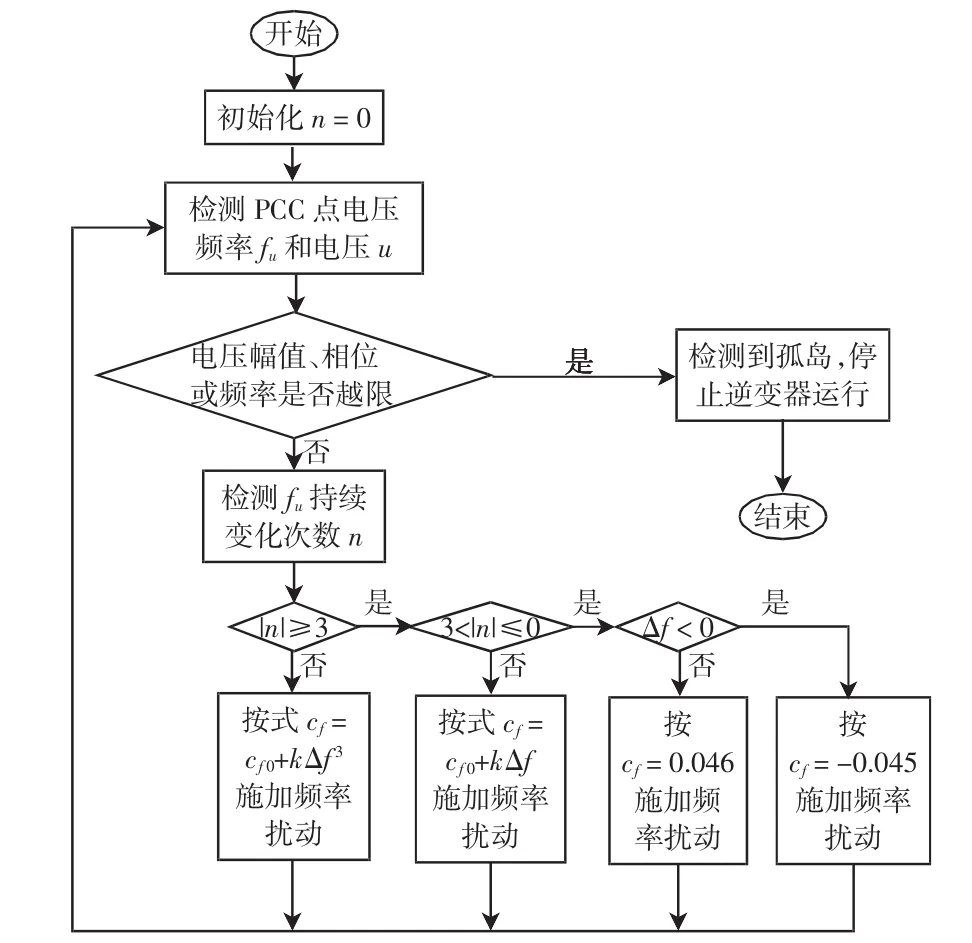
图3 改进的AFDPF检测方法流程Fig.3 Flow chart for improved AFDPF detectingmethod

由图4可知，主电网电压在0.06 s断开后，传统的AFDPF检测法对逆变器输出电流施加的扰动为cf=0.01+0.10Δf，逆变器在0.14 s时停止运行，即该检测法在0.08 s内成功检测到孤岛；由图5可知，0.06 s时主电网电压断开，改进的AFDPF孤岛检测算法对逆变器输出电流施加扰动为

图4 传统的AFDPF孤岛检测算法仿真结果Fig.4 Simulation resultsof traditionalAFDPF

图5 改进的AFDPF孤岛检测算法仿真结果Fig.5 Simulation resultsof improved AFDPF

图6 两种检测方法的谐波失真度Fig.6 THD of the two detectionmethods

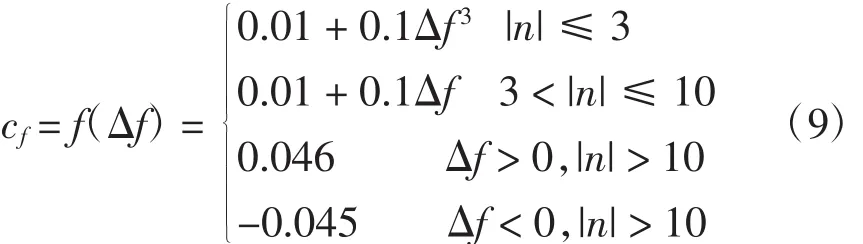
由于频率越限，逆变器在0.18 s时封锁PWM脉冲输出，逆变器输出电压和电流均降为0，在0.12 s内成功检测到孤岛并停止逆变器运行；由图6可知，传统AFDPF检测法逆变器输出电流谐波失真度THD为2.94%，改进的AFDPF检测法逆变器输出电流谐波失真度THD为1.82%，也就是说，改进的AFDPF检测法的THD明显小于传统的AFDPF检测法。仿真结果表明，改进的AFDPF算法由于引入了变量n，使孤岛检测所用的时间需要额外增加n累加的时间，即改进的AFDPF算法使孤岛检测时间变长。但是，从上面的仿真结果可知，引入的变量n虽然使检测速度变慢，但是与传统的AFDPF算法所用的检测时间仅仅相差0.04 s，并且都能在规定的检测时间（小于0.2 s）内成功检测到孤岛。也就是说，通过稍微降低孤岛检测的速度，改进的AFDPF算法能够大大降低电流谐波失真度，减小了频率扰动对电能质量的影响。同时，当存在孤岛时且3＜|n|≤10时，此处k=0.1，由图2的检测盲区图可知，该检测法使检测盲区右移，实现了在Qf0＜2.5条件下孤岛无盲区；当|n|＞10时采用先判断频率变化趋势再施加最强cf值的方法可以避免可能抵消负载频率变化而导致孤岛检测失败的缺点，从而减小了检测盲区。同时，由文献[9]可知，增大扰动cf，将使NDZ处于容性负载对应区域，推离实际电网系统（往往是感性负载）的分布区间，即相对减小了NDZ。

4 结语

本文根据光伏并网逆变器发电系统中正反馈主动频率偏移孤岛检测方法的原理，以Qf0为横坐标、Cnorm为纵坐标的坐标系分析了其检测盲区，并在此基础上对该检测方法中cf的表达式进行研究和改进，最后通过仿真验证了该改进方法的有效性。Matlab仿真结果表明：该改进的AFDPF检测法不仅检测盲区小，而且能在兼顾检测速度的同时，减小了电流谐波失真度，降低了扰动对电能质量的影响，对光伏并网发电系统防孤岛设计具有较好的应用价值。

[1]IEEEStd 929-2000，IEEE recommended practice for utility interface ofphotovoltaic systems[S].

[2]刘芙蓉，康勇，段善旭，等（Liu Furong，Kang Yong，Duan Shanxu，etal）.主动移频式孤岛检测方法的参数优化（Parameteroptimization ofactive frequency drift islanding detectionmethod）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（1）：95-99.

[3]张扬，张浩，张明，等（Zhang Yang，Zhang Hao，Zhang Ming，etal）.基于Qf0×Cnorm坐标系法的一个周期主动移频式孤岛检测盲区的研究（Islanding non-detection zone for active frequency driftof one cycle based on the Qf0× Cnormcoordinate method）[J].电网与清洁能源（Power System and Clean Energy），2011，27（5）：77-80.

[4]郑诗程，丁明，苏建徽，等（Zheng Shicheng，Ding Ming，Su Jianhui，etal）.光伏发电系统及其孤岛效应的仿真与实验研究（Simulation and experiment research of photovoltaic generation system and its islanding）[J].系统仿真学报（Journalof System Simulation），2005，17（12）：3085-088.

[5]杨海柱，金新民（Yang Haizhu，Jin Xinmin）.基于正反馈频率漂移的光伏并网逆变器反孤岛控制（Antiislanding control of gridd-connected photovoltaic inverter based on positive feedback frequency drift）[J].太阳能学报（Acta Energiae SolarisSinica），2005，26（3）：409-412.

[6]周诗嘉，陆格文，黎涛，等（Zhou Shijia，LuGewen，Li Tao，etal）.自适应主动频率偏移孤岛检测新方法（Adaptiveactive frequency shiftislanding detectingnewmethod forgrid-connected inverters）[J].电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2012，24（2）：78-82.

[7]Zheng Fei，FeiShumin，Zhou Xingpeng.A novel integrated islanding detectionmethod based on adaptive accelerating frequency drift[C]//International Conference on Electric Information and ControlEngineering.Wuhan，China：2011.

[8]Jung Y，Choi J，Yu B，etal.A novel active frequency drift method of islanding prevention for the grid-connected photovoltaic inverter[C]//36 th Power Electronic Specialists Conference.Recife Brazil：2005.

[9]林耀明，顾娟，单竹杰，等（Lin Yaoming，Gu Juan，Shan Zhujie，etal）.一种实用的组合式光伏并网系统孤岛效应检测方法（A practicalhybrid islandingdetectionmethod forgrid-connected photovoltaic system）[J].电力系统自动化（Automation ofElectric PowerSystems），2009，33（23）：85-89.

Improved Active Frequency Driftw ith Positive Feedback Islanding Detection Method

LIZhangxia，LUOXiaoshu，LIAOZhixian，CHENYahuan
（CollegeofElectronic Engineering，GuangxiNormalUniversity，Guilin 541004，China）

Islanding isa basic problem of photovoltaic grid-connected inverter generation system.Islanding detection mustbe accurate and fast，and should deduce its negative influence on the power quality asmuch as possible．In this paper，the basic principles of active frequency drift（AFD）method and active frequency driftwith positive feedback（AFDPF）method are expounded，the non-detection zone（NDZ）of AFDPFmethod is analyzed.And on thisbasis，an improved AFDPFmethod is proposed，which achieves frequency shiftby a disturbance thatare expressed by piecewise function.At last，this improvedmethod issimulated on Matlab/Simulink platform.The result indicates that the improved AFDPFmethod iseffective and reduces totalharmonic distortion（THD）.

photovoltaic（PV）grid-connected inverter；islanding detection；active frequency driftwith positive feedback（AFDPF）；non-detection zone（NDZ）；totalharmonic distortion（THD）

TM464

A

1003-8930（2015）04-0013-05

10.3969/j.issn.1003-8930.2015.04.003

黎璋霞（1988—），女，硕士研究生，研究方向为光伏并网发电理论与应用。Email：lizhangxia012@163.com

201-08-20；

2013-10-25

国家自然科学基金资助项目（11262004）；广西科学研究与技术开发项目（桂科攻1348017-2）；广西壮族自治区研究生教育创新计划项目（YCSZ2012061）

罗晓曙（1961—），男，通讯作者，博士，教授，研究方向为非线性电路理论及非线性系统控制﹑复杂网络理论与应用﹑工业自动化控制。Email：lxs@mailbox.gxnu.edu.cn

廖志贤（1986—），男，硕士，讲师，研究方向为光伏并网发电理论与应用。Email：zhixianliao@mailbox.gxnu.edu.cn