考虑风险传导情形的供应风险评估方法

张 川， 杨文雯， 于 超

(东北大学 工商管理学院,辽宁 沈阳 110819)



考虑风险传导情形的供应风险评估方法

张 川， 杨文雯， 于 超

(东北大学 工商管理学院,辽宁 沈阳 110819)

针对考虑风险传导情形的供应风险评估问题，提出了一种基于贝叶斯网络的供应风险评估方法。该方法中，通过识别引起供应链中各节点企业供应风险的关键风险因素，构建一个贝叶斯网络，并依据贝叶斯公式计算考虑风险传导情形下供应风险的发生概率，在此基础上，对考虑风险传导的供应风险进行评估。最后，通过一个算例说明了该方法的可行性和有效性。

风险评估；供应风险；贝叶斯网络；风险传导

0 引言

供应链风险具有传导性，即供应链中的一系列过程是由多个企业参与的，企业之间存在密切联系，每个成员企业的风险会随着网络结构转移给其他企业，甚至整个供应链[1]。例如，2000年美国新墨西哥州飞利浦公司第22号芯片厂发生火灾，导致供应链下游企业爱立信损失4亿美元的销售额[2]。供应链风险传导事件在现实生活中普遍存在，给供应链上的相关企业带来很大的损失。供应风险是指企业在供应环节中受内外因素影响给企业的成本和利润带来的不确定性。Tang和Tomlin[3]对供应风险进行了描述，认为供应风险来源于供应商的不确定性，具体表现为外界因素或企业内部因素致使供应商的生产不平稳或常规供应商的有效供货数量可能与下游企业的实际订货量不同。在供应链环境下，企业的需求风险、机器故障、运输风险等风险事件的发生均有可能使供应风险发生的概率变大，而供应商供应风险事件的发生不仅会给企业自身带来巨大的经济损失，而且有可能影响到其下游企业的加工生产，进而导致其下游企业发生供应风险事件，甚至造成整条供应链的生产停滞，这就是供应风险的传导性。有效地评估供应风险是防范和应对供应风险的前提和基础，如果供应风险评估出现了偏差，最终会影响供应风险控制策略的实施，导致企业决策失误，给企业带来损失。因此，考虑风险传导情形的供应风险评估问题值得特别关注，对此研究具有理论意义和现实意义。

近年来，可以看到有关供应链风险评估方面的研究成果[4～10]。国内外对于风险传导的研究主要侧重在金融风险传导[11～15]以及企业风险传导等方面的研究[16～18]。目前，关于考虑供应链风险传导的供应风险评估方法的研究所见甚少，但可以看到一些相关的研究成果，例如，Zegordi和Davarzani[19]建立了基于Petri网的供应链中断风险传导模型，并分析了中断风险在供应链上的传导以及带来的影响；Ghadge[20]用系统思想的方法模拟了风险在供应链上的传导过程。魏海蕊[21]运用基于OWA算子的方法模拟了中断风险在供应链上的传导，并评估了考虑风险传导时中断风险给各节点企业带来的经济损失；程国平和刘勤[22]提出了供应链风险传导路径动态变化模型，并详细研究了传导过程中不同属性风险之间强藕合效应发生的条件；陈玉印等[23]运用综合模糊评判法对供应链节点间的柔性进行了测度，依据供应链节点间的柔性度大小不同，用动态规划中最短路问题寻找风险在供应链上传导的关键路径，并讨论了风险源在关键路径和风险源不在关键路径两种情形下的风险传导路径。已有的文献对供应链风险传导的载体、路径及机理进行了研究，而考虑风险传导情形的供应风险评估方法的研究所见甚少。需要指出的是，贝叶斯网络[14]的结构和推理过程具有适合风险评价建模和分析的特点[25]，贝叶斯网络的结构可以表示变量间的不确定性关系和多态性特征，贝叶斯网络的因果推理可以计算各种风险条件下企业发生风险的联合概率。鉴于此，本文给出一种基于贝叶斯网络的供应风险评估方法。该方法中，首先依据风险因素之间的“因果关系”构建贝叶斯网络，然后利用贝叶斯公式计算考虑风险传导情形的供应风险的发生概率，进而对供应风险进行评估。

1 问题描述

下面给出用于描述考虑风险传导情形的供应风险评估问题中所涉及的集和量。

·S={S1,S2,…,Sn}：供应同种产品的n个供应商的集合，其中Si表示第个供应商，i=1,2,…,n。

·M：一个生产商企业。

·K={KS1,KS2,…,KSn}：n个供应商的供应风险集合，其中KSi表示第i个供应商的供应风险，i=1,2,…,n。

·KM：生产商的供应风险。

·RF={RFi_j|i=1,…,n,n+1,j=1,…,m}：引起n个供应商和一个生产商供应风险的风险因素集合，其中RFi_j表示引起第i个节点企业供应风险的第j个风险因素。

·PS={pS1,pS2,…,pSn}：n个供应商的供应风险发生概率的集合，其中pSi表示第i个供应商供应风险的发生概率，i=1,2,…,n。

·pM：生产商供应风险的发生概率。

·lM：生产商供应风险引起的损失。

针对由多个供应商和一个生产商构成的一个二级供应链，由于供应商的供应风险是由多种风险因素引起的，且供应商供应风险的发生会传导给生产商，使生产商采购风险的发生概率变大，从而使生产商面临更大的供应风险。本文要解决的问题是，识别引起供应商和生产商供应风险的风险因素，根据风险因素之间的“因果关系”构建贝叶斯网络，依据各风险因素之间的条件概率和根节点风险因素发生的先验概率，评估考虑风险传导情形的生产商供应风险的风险值。

2 基于贝叶斯网络的供应风险评估模型

为了解决上述问题，下面阐述本文提出的基于贝叶斯网络的供应风险评估方法。在该方法中，首先识别引起供应商和生产商供应风险的风险因素，以及各风险因素之间的“因果关系”，构建贝叶斯网络；然后，基于贝叶斯网络中各节点风险的条件概率和根节点风险的先验概率，依据贝叶斯公式推理考虑风险传导情形的供应风险的发生概率；进一步地依据风险评估公式对生产商供应风险进行评估。下面给出该方法的具体描述。

2.1 构建贝叶斯网络

针对考虑风险传导情形的供应风险评估问题，首先需要构建供应链风险的贝叶斯网络，而贝叶斯网络的构建过程，实质上是一个依据供应链上的企业所处供应链的特点，由子节点向父节点逐层分析和识别可能导致该企业供应风险的各种风险事件的过程。例如，针对供应商而言，可能导致其供应风险的因素有生产风险、需求风险和运输风险三个方面，则以供应商供应风险为子节点，可以得到生产风险、需求风险和运输风险三个父节点。根据贝叶斯网络的三元组表示，记N=((I,E),P)为一个具有N个节点的贝叶斯网络，G(I,E)表示一个有向无环图[13]，其中I={I1,…,In}为网络中的变量集合，代表供应链各企业中的供应风险以及引起供应风险的风险因素；E为有因果关系的两变量之间有向边的集合，代表风险之间的“因果关系”；P为网络中各变量的条件概率集合，代表各风险之间的条件概率。对于任意的随机变量，如果给定所有的根节点先验概率和条件概率分布，可以得到包含所有节点的联合分布为：

(1)

其中pa(Ir)为变量Ir在有向无环图G中的父节点。

那么通过寻找引起供应商和生产商供应风险的风险因素及识别风险因素之间的“因果关系”，可以构建一个贝叶斯网络。

图1 单个父节点的贝叶斯网络

2.2 基于贝叶斯网络的供应风险评估

当确定了贝叶斯网络结构后，通过历史数据和专家评估给出各个风险节点的条件概率表和根节点风险的先验概率。每个风险节点的条件概率表中需包括该节点在其所有父节点不同状态组合情况下处于某种状态的概率。

如图1展示了一个贝叶斯网络，图中的风险节点Ii具有单个父节点Ij。tr为风险节点Ir的状态，其中tr∈{T,F}，tr=T表示风险Ir发生，tr=F表示风险Ir不发生。风险节点Ii和父节点Ij的条件概率为p(Ii=ti|Ij=tj)，Ij的先验概率为p(Ij=tj)。

通过历史数据和专家评估可以得到条件概率p(Ii=T|Ij=T)、p(Ii=T|Ij=F)以及父节点的先验概率p(Ij=T)。因此，依据条件概率和根节点的先验概率，利用贝叶斯公式可以得到风险节点Ii发生的概率，即p(Ii=T)=p(Ii=T|Ij=T)·p(Ij=T)+p(Ii=T|Ij=F)·p(Ij=F)。

图2 多个父节点的贝叶斯网络

图2展示了具有多个父节点的贝叶斯网络，图中风险节点Ii有k个父节点分别为I1,I2,…,Ik。每个风险节点Ir对应一个状态为tr，tr∈{T,F}，tr=T表示风险Ir发生，tr=F表示风险Ir不发生。风险节点Ii和父节点的条件概率为p(Ii=ti|I1=t1,I2=t2,…,Ik=tk)，根节点的先验概率为p(Ij=tj)。依据条件概率表和根节点的先验概率，利用贝叶斯公式可得到节点Ii发生的概率。

在贝叶斯网络中，计算风险节点处于某种状态时的概率均可以分解成图1和图2两种情况。因此，基于贝叶斯网络，依据历史数据由专家给出风险之间的条件概率和根节点风险的先验概率，可以求出每个供应商供应风险的发生概率及考虑供应商供应风险向生产商采购风险传导时生产商供应风险的发生概率。

记rM表示生产商的供应风险值，其计算公式为

rM=pMlM

(2)

3 算例

本部分以某冷却系统生产企业的一批冷却系统订单的供应风险评估问题为背景来说明上文提出方法的潜在应用。

生产商M是一家冷却系统生产企业，该企业与其供应链下游的某气体压缩机生产企业有着长期合作的关系，负责向其下游的气体压缩机生产企业供应冷却系统。现生产商M接到了一批冷却系统的生产订单，该批次订单要求保质保量按时供货，若订单产品不能及时供货，预计会给生产商带来20万的经济损失。在合同签订之前，生产商M欲对该批次订单的供应风险进行评估，以决定是否要接收该批冷却系统订单以及如何有效的降低和应对订单产品的供应风险。综合考虑订单产品所需的核心部件及企业自身当前的库存储备情况，生产商M需要向其上游的两个供应商(S1和S2)采购同种产品零部件。经分析得到订单产品生产涉及的供应链是一个由两个供应商(S1和S2)和一个生产商(M)组成的二级供应链，识别引起KS1的关键风险因素分别为：机器故障(RF1_1)、采购风险(RF1_2)、生产风险(RF1_3)、需求风险(RF1_4)和运输风险(RF1_5)；识别引起KS2的关键风险因素分别为：人员风险(RF2_1)、机器故障(RF2_2)、采购风险(RF2_3)、生产风险(RF2_4)和运输风险(RF2_5)；识别引起KM的关键风险因素分别为：采购风险(RF3_1)、信息风险(RF3_2)、生产风险(RF3_3)、需求风险(RF3_4)和运输风险(RF3_5)。

供应商供应风险的发生会使生产商采购风险发生的概率大大增加，因此，通过分析风险之间的“因果关系”，对整个供应链建立的贝叶斯网络如图3所示。根据历史数据，由专家给出供应商S1生产风险(RF1_3)的条件概率表如表1所示，由专家给出供应商S1生产风险的根节点风险(即机器故障)的发生概率和采购风险的发生概率分别为p(RF1_1=t1)=0.2和p(RF1_2=t1)=0.2，供应商S1供应风险KS1的条件概率表如表2所示，供应商S1供应风险的根节点风险(即需求风险)的发生概率和运输风险的发生概率分别为p(RF1_4=T)=0.3和=p(RF1_5=T)0.3。

图3 供应链风险的贝叶斯网络

S1生产风险父节点的状态S1生产风险的状态RF1_3=TRF1_3=FRF1_1=T,RF1_2=T0.90.1RF1_1=T,RF1_2=F0.60.4RF1_1=F,RF1_2=T0.70.3RF1_1=F,RF1_2=F0.20.8

表2S1供应风险的条件概率

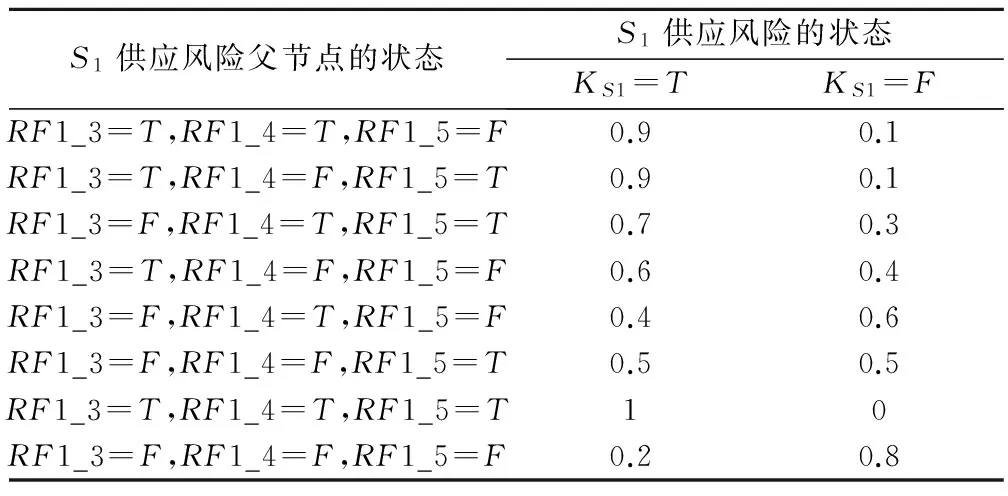
S1供应风险父节点的状态S1供应风险的状态KS1=TKS1=FRF1_3=T,RF1_4=T,RF1_5=F0.90.1RF1_3=T,RF1_4=F,RF1_5=T0.90.1RF1_3=F,RF1_4=T,RF1_5=T0.70.3RF1_3=T,RF1_4=F,RF1_5=F0.60.4RF1_3=F,RF1_4=T,RF1_5=F0.40.6RF1_3=F,RF1_4=F,RF1_5=T0.50.5RF1_3=T,RF1_4=T,RF1_5=T10RF1_3=F,RF1_4=F,RF1_5=F0.20.8

由贝叶斯网络进行推理可以得到供应商S1供应风险的发生概率为pS1=0.48。

根据历史数据，由专家给出供应商S2生产风险的根节点风险(即机器故障)的发生概率为p(RF1_2=T)=0.3；采购风险的发生概率为p(RF2_2=T)=0.2；人员风险的发生概率为p(RF2_3=T)=0.4；供应商S2生产风险的条件概率如表3所示。

根据历史数据，由专家给出供应商S2供应风险的根节点风险(即运输风险)的发生概率为p(RF2_5=T)=0.3，供应商S2供应风险的条件概率如表4所示。

由贝叶斯网络进行推理可以得到供应商S2供应风险的发生概率为pS2=0.46。

在计算得到供应商S1和供应商S2供应风险发生概率的基础上，由专家根据历史数据给出供应商的供应风险和生产商的采购风险之间的条件概率表(CPT)，具体如表5所示。

表3 S2生产风险的条件概率

S2生产风险父节点的状态S2生产风险的状态RF2_4=TRF2_4=FRF2_1=T,RF2_2=T,RF2_3=F,0.70.3RF2_1=T,RF2_2=F,RF2_3=T,0.80.2RF2_1=F,RF2_2=T,RF2_3=T,0.90.1RF2_1=T,RF2_2=F,RF2_3=F,0.40.6RF2_1=F,RF2_2=T,RF2_3=F,0.50.5RF2_1=F,RF2_2=F,RF2_3=T,0.60.4RF2_1=T,RF2_2=T,RF2_3=T,10RF2_1=F,RF2_2=F,RF2_3=F,0.20.8

表4 S2供应风险的条件概率

表5 供应商供应风险和生产商采购风险之间的条件概率

供应风险的状态M采购风险的状态RF3_1=TRF3_1=FKS1=T,KS2=T0.90.1KS1=T,KS2=F0.70.3KS1=F,KS2=T0.40.6KS1=F,KS2=F0.20.8

由贝叶斯网络进行推理可计算出考虑供应商供应风险向生产商采购风险传导时生产商M采购风险发生的概率为p(RF3_1)=0.53。

假设不考虑供应商供应风险向生产商采购风险传导时生产商M采购风险发生的概率为0.2。

根据历史数据和专家评估给出生产商M信息风险的发生概率为p(RF3_2)=0.2；运输风险的发生概率为p(RF3_5)=0.2；生产商M生产风险的条件概率为p(RF3_3=T|RF3_1=T)=0.6，p(RF3_3=T|RF3_1=F)=0.1；需求风险的条件概率为p(RF3_4=T|RF3_2=T)=0.4，p(RF3_4=T|RF3_2=F)=0.2；M供应风险的条件概率如表6所示。

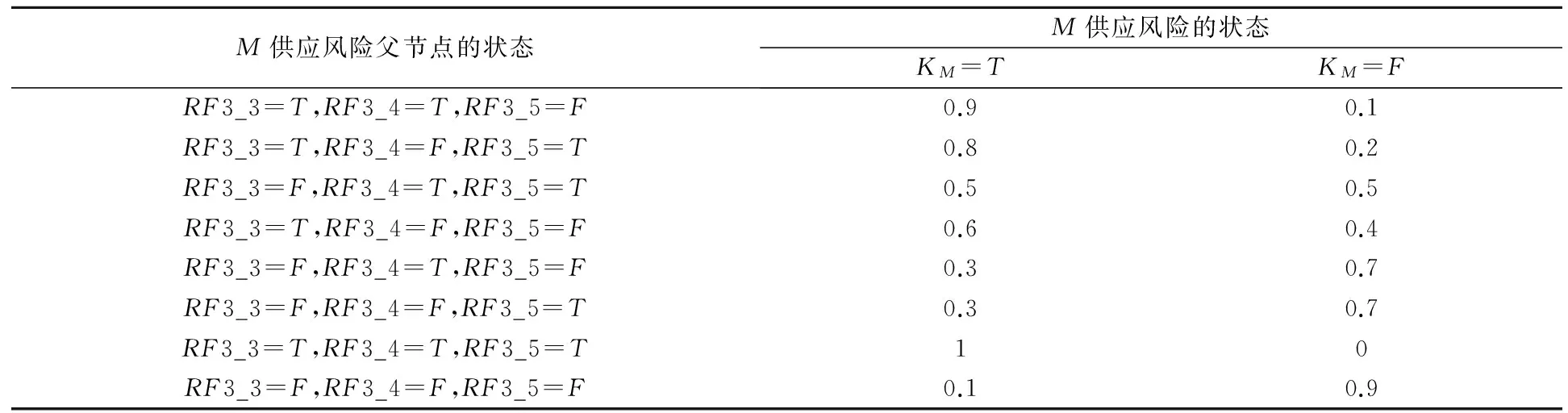
表6 M供应风险的条件概率

通过贝叶斯网络推理可计算出考虑供应商风险传导和不考虑供应商风险传导两种情形下生产商发生供应风险的概率，具体结果分别为：考虑供应商供应风险传导时生产商供应风险发生的概率为0.49；不考虑供应商供应风险传导时生产商供应风险发生的概率为0.36。通过专家评估，发生供应风险给企业造成的损失为20万元。依据公式(2)，不考虑供应商的供应风险向生产商的采购风险传导时，供应风险的风险值为7.2万元；考虑供应商的供应风险向生产商的采购风险传导时，供应风险的风险值为9.8万元。可见，供应商供应风险的传导作用给生产商增加了2.6万元的供应风险量。

从计算结果可以看出，生产商M供应风险发生的概率较大，而供应风险主要来源于采购风险，若决定接受这批冷却系统的订单，必须加强采购管理，如有目的性地增加与其上游零部件供应商之间签订的采购合同的条款，增加上游零部件供应商未能及时供货所需支付的违约金，将风险转移给上游零部件供应商或与上游零部件供应商共同担负风险，也可以考虑更换供应商或增加备用供应商。

4 结束语

本文给出了一种考虑风险传导情形的供应风险评估方法。该方法是依据供应链中各风险因素之间的关系构建贝叶斯网络，并运用贝叶斯公式计算供应商供应风险发生的概率，进而对供应商的供应风险进行评估。需要指出的是，该方法与已有方法相比，其特点是：针对供应链中各风险因素之间的关系构建贝叶斯网络，不仅清晰展现了供应链中各风险因素之间的影响关系，而且较好反应了供应链中各节点企业之间供应风险的传导性。本文的方法具有逻辑清晰、计算简单等特点，为解决现实中的供应风险评估问题提供了一种新途径或新思路，具有较好的实际应用价值。

[1] 马丽,张光明,李平.供应链风险传递机制与传递路径研究[J].科技情报开发与经济,2007,17(31): 96-98.

[2] 程国平,邱映贵.供应链风险传导模式研究[J].武汉理工大学学报,2009,22(2):36- 41.

[3] Tang C, Tomlin B. The power of flexibility for mitigating supply chain risks[J]. International Journal of Production Economics, 2008, 116(1): 12-27.

[4] 顾孟迪,雷鹏.风险管理[M].北京：清华大学出版社,2005.

[5] Prater E, Biehl M, Smith M A. International supply chain agility-tradeoffs between flexibility and uncertainty[J]. International Journal of Operations & Production Management, 2001, 21(5/6): 823- 839.

[6] Nagurney A, Dong J. Management of knowledge intensive systems as supernetworks: modeling, analysis, computations, and applications[J]. Mathematical and Computer Modelling, 2005, 42(3): 397- 417.

[7] Zsidisin G A, Ellram L M, Carter J R, et al. An analysis of supply risk assessment techniques[J]. International Journal of Physical Distribution & Logistics Management, 2004, 34(5): 397- 413.

[8] 王永刚,张金隆,唐扬洋,等.核电站备件供应风险测度模型研究[J].武汉理工大学学报:信息与管理工程版,2007,29(3):72-75.

[9] Rosenau-Tornow D, Buchholz P, Riemann A, et al. Assessing the long-term supply risks for mineral raw materials—a combined evaluation of past and future trends[J]. Resources Policy, 2009, 34(4): 161-175.

[10] 丁伟东,刘凯,贺国先.供应链风险研究[J].中国安全科学学报,2003,13(4):64- 66.

[11] Forbes K J, Rigobon R. No contagion, only interdependence: measuring stock market comovements[J]. The Journal of Finance, 2002, 57(5): 2223-2261.

[12] Engle R. New frontiers for ARCH models[J]. Journal of Applied Econometrics, 2002, 17(5): 425- 446.

[13] Gallo G M, Velucchi M. Market interdependence and financial volatility transmission in east asia[J]. International Journal of Finance & Economics, 2009, 14(1): 24- 44.

[14] Hong Y, Liu Y, Wang S. Granger causality in risk and detection of extreme risk spillover between financial markets[J]. Journal of Econometrics, 2009, 150(2): 271-287.

[15] 陈王,魏宇,淳伟德,等.中国股市与周边股市波动风险传导效应研究[J].中国管理科学,2011,19(6):31-39.

[16] 夏喆,邓明然,黄洁莉.企业风险传导进程中的耦合性态分析[J].上海管理科学,2007,29(1):4- 6.

[17] Fu Y, Li M, Chen F. Impact propagation and risk assessment of requirement changes for software development projects based on design structure matrix[J]. International Journal of Project Management, 2012, 30(3): 363-373.

[18] Feng N, Wang H J, Li M. A security risk analysis model for information systems: causal relationships of risk factors and vulnerability propagation analysis[J]. Information sciences, 2014, 256: 57-73.

[19] Zegordi S H, Davarzani H. Developing a supply chain disruption analysis model: application of colored petri-nets[J]. Expert Systems with applications, 2012, 39(2): 2102-2111.

[20] Ghadge A, Dani S, Kalawsky R. Systems thinking for modeling risk propagation in supply networks[C]∥Industrial Engineering and Engineering Management(IEEM), 2011 IEEE International Conference on. IEEE, 2011: 1685-1689.

[21] Wei H, Dong M, Sun S. Inoperability input-output modeling(IIM)of disruptions to supply chain networks[J]. Systems Engineering, 2010, 13(4): 324-339.

[22] 程国平,刘勤.供应链风险传导路径变化研究[J].价值工程,2009,28(4):1-3.

[23] 陈玉印,宋国防,张莹.基于供应链节点间柔性的风险传导关键路径研究[J].物流技术,2010,29(23):147-149.

[24] Jensen F V. An Introduction to bayesian networks[M]. London: UCL Press, 1996.

[25] Siu N O, Kelly D L. Bayesian parameter estimation in probabilistic risk assessment[J]. Reliability Engineering & System Safety, 1998, 62(1): 89-116.

Supply Risk Evaluation Method Considering Risk Propagation

ZHANG Chuan, YANG Wen-wen, YU Chao

(SchoolofBusinessAdministration,NortheasternUniversity,Shenyang110819,China)

In this paper, a method for supply risk evaluation based on Bayesian network is proposed to solve the supply risk evaluation problem considering the risk propagation. In this method, firstly, a Bayesian network is constructed via identifying key risk factors which may cause the supply risk of each node enterprise. According to Bayes formula, the probability of supply risk considering the risk propagation is calculated. On this basis, supply risk is evaluated considering the risk propagation. Finally, a numerical example is used to illustrate the feasibility and validity of the proposed method.

risk evaluation; supply risk; Bayesian network; risk propagation

2013-11- 07

国家自然科学基金资助项目(71271051)；辽宁省教育厅人文社会科学重点研究基地专项项目(ZJ2014020)

张川(1969-),男,辽宁本溪人,博士,副教授,研究方向:运筹与管理。

C394

A

1007-3221(2015)04- 0172- 06