竞争环境下截流问题的选址-价格模型

申瑞玲, 霍佳震, 王 茜



竞争环境下截流问题的选址-价格模型

申瑞玲1, 霍佳震2, 王 茜3

(1.河南财经政法大学 数学与信息科学学院，河南 郑州 450000； 2.同济大学 经济与管理学院，上海 200092; 3.河南工业大学，河南 郑州 450000)

研究了竞争环境下考虑产品定价的截流设施选址问题。连锁企业在市场上新建设施时，市场上已有属于竞争对手的设施存在，在连锁企业新建设施位置确定之后，两个企业关于产品定价进行双寡头完全信息非合作博弈。定义了效用函数，引入Huff模型，以企业利润最大为目标，建立双层规划模型，证明了模型纳什均衡价格的存在性，并构造启发式算法对模型进行求解。算例分析表明，该算法求解结果较为理想，可用于大中型网络的规划选址问题。

运筹学；截流设施选址；选址-价格；纳什均衡；模拟退火算法

0 引言

连锁企业在进入某个市场时，如果市场上没有其他企业的同类设施存在，则企业在市场上处于垄断地位，如果市场上已有其他企业的同类设施存在，则企业在市场上展开竞争[1]。在竞争的过程中，商业企业追求的是利润的最大化。为了获取最大利润，企业在进入市场时，除了要考虑选址的地点之外，还要考虑其他一些因素，如产品的定价，竞争对手的反应等

竞争选址模型最早由Hoteling[2]提出，假设消费者均匀分布在一条直线上，对两个冰淇淋商贩的选址问题进行了研究；Hoover[3]首先对选址-价格(location-price)问题进行了研究。此后学者们在对选址-价格模型的研究中，将产品定价分为两种情况，一种是出厂价格(mill price)，企业对产品统一定价，消费者与企业设施之间的运输成本由消费者承担，另一种是交货价格(delivered price)，企业与消费者之间的运输成本由企业承担，企业对各个区域消费者分别定价[4]。Serra和Revelle[5]假设竞争双方对产品定价为出厂价格，顾客到使其支付总成本最低的设施接受服务，构造PMAXCAP模型，研究了先进入市场的企业会对后进入市场的企业的决策做出反应的情况下，后进入市场的企业如何选址和确定价格，以使其利润最大的问题；Perez等[6]讨论了企业产品定价分别为出厂价格和交货价格的情况下，纳什均衡解存在的条件；Aboolian等[7]研究了先进入市场的企业不会对其产品定价进行调整，但是消费者需求存在弹性的情况下，构造CFLUPM模型对后进入市场的企业的选址和定价策略进行了研究，并讨论了需求弹性系数对企业决策的影响；Garcia等[4]研究了产品定价为交货价格，后进入市场的企业的候选选址点是网络中的任意点和只能是网络中的节点两种情况下，后进入市场企业的选址-定价问题，并证明了在一定情况下，先进入市场的企业的利润随着后进入市场上企业新建设设施数的增加而增加；Pelegrin等[8]研究了定价为交货价格，且存在市场扩张的情况下，连锁企业如何选择扩建设施点并如何对产品定价的问题。

传统的设施选址假设设施服务对象位于网络中各个节点，但是对有些设施，如加油站，加气站，ATM，便利商店等，其服务对象主要是过往的顾客流，截流设施选址问题主要对此类问题进行研究。Hodgson[9]和Berman[10]各自提出了截流设施模型，对截流选址模型进行了开拓性的研究；Berman和Krass[11]将空间交互作用模型引入到截流选址模型中，提出了FISIM模型，讨论了消费者偏离原路径行驶情况下的竞争环境下截流选址模型，为截流设施选址问题的研究提供了新的思路；在此基础上，Wu和Lin[12]研究了竞争环境下的截流设施选址问题；杨珺等[13]研究了带服务半径的截流设施选址问题；胡丹丹等[14]研究了考虑顾客等待时间的截流设施选址问题；Zeng 等[15,16]研究了考虑消费者购物区位偏好的截流设施选址问题；Tanaka和Furuta[17]假设不同大小的设施吸引力不同，研究了企业同时确定选址地点和设施大小的问题。

本文对竞争环境下考虑产品定价的设施选址问题进行研究。问题描述为：连锁企业(企业A)在进入某个市场时，市场上已有属于竞争对手(企业B)的设施存在，在企业A确定其选址地点和产品定价之后，为使本企业利润最大化，企业B对其产品定价进行调整。假设两个企业销售完全相同的产品，同一企业在其各个设施点处定价相同，产品定价为出厂价格，消费者到设施点处购买产品的交通费用由消费者承担。

1 模型建立

我们用G(N,A)表示网络，其中N为网络中的节点集，A为网络中的边集；P为网络中非零流量的路径集合,p∈P;Np为路径p上的节点集合；fp为路径p上顾客流量；E为网络中企业B已有的设施点集合,k∈E;M为企业A新建设施点集合,j∈M;m为企业A拟新建设施数目；gj为企业A在j处新建设施的建设成本,j∈M;cA,cB分别表示企业A，企业B产品的成本价；pA,pB分别表示企业A，企业B对产品的定价。

在截流选址模型中，我们用dpj表示路径p上的顾客到节点j处接受服务时偏离原路径的距离。本文中我们定义偏离距离dpj的计算公式为：假设s,e分别是路径p的起点和终点，若p上的顾客到j点接受服务，则偏离距离dpj=dpj+dje-dse。

根据以上分析，建立模型如下：

(1)

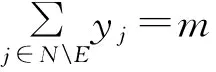
(2)

pA≥cA

(3)

upj=max(U-(pj+αdpj)αp,0)

(4)

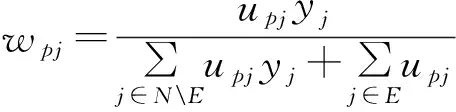
(5)

yj∈{0,1}

(6)

maxπB(pA,pB,Y)=(pB-cB)∑p∈P∑j∈Efp×wpj

(7)pB≥cB

(8)

其中目标函数(1)式表示企业A的总利润，其中第一项表示企业A的总收入，第二项表示企业A的选址成本，约束条件(2)式表示企业A新建设施个数为m个，(3)表示企业A的产品定价pA不低于产品进价cA，(4),(5)在前面已经解释，(6)式是0-1约束，下层目标函数(7)式表示企业B的总利润最大，(8)表示企业B的产品定价pB不低于产品进价cB

2 模型解的存在性

整个决策过程可以分为两个阶段：第一阶段，确定企业A选址地点。在此阶段，企业A需考虑下一阶段的价格博弈。第二阶段，确定产品定价。对企业A新建设施点集合，在考虑对方策略的情况下，基于本企业利润最大化的原则，两个企业确定各自产品定价，这一决策过程可以看作是一个完全信息非合作博弈的过程，博弈的结果是双方产品定价为目标函数的纳什均衡解。接下来我们将证明模型纳什均衡解的存在性。

纳什均衡策略是每一个参与者针对其他参与者所选策略的最优反应策略[18]，为了证明本模型中纯策略纳什均衡解的存在性，我们首先引入Debreu定理。

定理1 (Debreu) 在策略博弈中,如果每个局中人的纯策略空间Si是欧氏空间上的非空紧凸子集，支付函数连续且关于Si拟凹，那么该博弈存在一个纯策略纳什均衡。

命题1πΑ,πΒ分别关于pΑ,pB是拟凹的。

(9)

同理可证，πB关于pB是凹函数。

根据凹函数与拟凹函数的性质，πΑ,πB分别关于pA,pB是拟凹的。

从效用函数的定义可以看到，一定存在某个值pAmax，当企业A的产品定价pA大于pAmax时，企业A对所有路径上的顾客流效用为零，此时企业A利润为零，因此pA的取值范围为 [cΑ,pAmax], 同样的，定义pB的取值范围为[cB,pBmax] 。

命题2 问题P存在纯策略纳什均衡解。

证明 在此模型中，策略空间pA=[cΑ,pAmax],pB=[cB,pBmax],显然pA,pB是有界闭凸集。由连续函数的性质知，πΑ,πB是连续函数，根据推论1,πΑ,πB分别关于pA,pB是拟凹的，模型满足定理1纯策略纳什均衡解存在的所有条件，命题得证。

3 算法设计

由于模型的目标函数是非线性函数，且目标函数中wpj的值只有在pA,pB,Y确定后才能确定，因此不能使用传统的规划的方法进行求解。基于此，我们构造启发式算法进行求解。

模拟退火算法[19]模拟金属的退火过程，它从某一较高初温出发，伴随温度参数的不断下降，在解空间中随机搜寻目标函数的全局最优解，为了避免陷入局部最优解，算法使用双向搜索技术，若新求得的解优于当前解，则接受新求得的解为当前解，否则，以一定的概率接受新求得的解为当前解。模拟退火算法已在理论上被证明是一种以概率1收敛于全局最优解。研究表明，较高质量的初始解不仅可以提高模拟退火算法的收敛速度，而且提高算法最终解的质量。本文中我们使用贪婪算法所求得的解为模拟退火算法的初始解。

具体算法如下：算法分为两个阶段，第一阶段使用贪婪算法对问题进行求解，将贪婪算法求得的问题的解作为问题的初始解，在第二阶段使用模拟退火算法对其进行优化，具体步骤如下：

第一阶段：贪婪算法求解问题初始解：

Step 1M0←Φ,k←1;

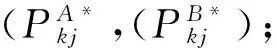
Step 4Mk←Mk-1∪{j*},k←k+1;

Step 5 如果k=m或者N-E-Mk=Φ, 终止计算；否则，转入Step 2.

第二阶段：模拟退火算法：

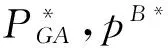
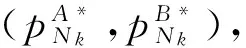
Step 3 :k←k+1,tk+1←α×tk. 若满足终止条件，则终止计算，否则转入Step 2.

注1：模拟退火算法包含一个内循环过程和一个外循环过程，本文中，我们将外循环的终止条件设置为温度t降到指定温度，内循环终止条件为迭代次数达到事先给定的值，内循环中Mk的邻域由交换Mk中任意两个元素的位置得到。

注2：纳什均衡解的求解。虽然我们在第三部分证明了模型纳什均衡解的存在性，但是却很难求得其解析解。这是因为，给定企业A的选址点，则两个企业的价格均衡解需由求解以下非线性方程组得到：

由于各个方程组里各个等式的高度非线性性，要求得方程组的解析解几乎是不可能的，因此本文中我们使用Serra和Revelle[4]提出的price-search算法进行求解。

4 算例分析

4.1 小规模算例

我们随机生成节点数为10,15,20，路径数为20,30,40的随机网络，企业B已有的设施数目为1,2，企业A拟新建设施数目m=2,3，对每组情况，随机生成30组算例。每组算例中，路径p上的顾客流fp～N(100,30),企业A在各个节点处的选址成本gj∈[400,500],两个企业的产品成本cA=cB∈[4.5,5],效用函数中参数U∈ [8,10],α,αp∈ [0,1]。

为了检验本文所提启发式算法的有效性，我们将本文所提算法的试验结果与枚举算法的计算结果进行比较。但是，在枚举算法求解的过程中，对算法得到的任何一个问题的可行解，使用price-search 算法求解两个企业的纳什均衡价格。因为在求解的过程中使用了price-search 算法，枚举算法求得的问题的解不一定是模型的最优解，但是算法给了我们一个模型解的上界，用于检验本文所提算法的有效性。两种算法结果的比较如表1 所示。从表1可以看出，本文所提算法的计算结果与枚举算法的计算结果基本一致，算法是有效的。

表1 本文算法与枚举算法计算结果比较

4.2 大规模算例

图1 示例网络

如图1所示，网络中节点数为60，路径数为150，各个路径上的需求量服从均值为1000，方差为300 的正态分布，企业B已在节点14,48,57处各有一个设施，企业A拟新建设施个数为5，两个企业产品成本价均为8，消费者偏离原路径行驶单位距离的成本为0.25，各潜在设施点的选址成本均为1000。

我们用Matlab进行编码，在Intel Core i3-350M处理器，2G内存的计算机上进行仿真实验，其中模拟退火算法初始温度为4000度，降温系数0.99，终止温度400度，内循环每次迭代步长为10，企业A新建设施个数分别为1,2,3,4,5的情况下，对示例网络进行了仿真实验，实验结果如表2所示。

表2 算法运算结果

从表2可以看到，随着企业A新建设施数的增加，企业A对产品的定价逐步增高，企业B产品定价逐渐降低。从目标函数的定义可以看到，其他因素不变的情况下，某个企业产品价格的提高会造成两方面的影响，一是其单位产品利润的提高，二是企业市场占有率的降低，如何权衡利弊，制定合适的价格以获取最大利润，是一个非常复杂的问题。从表1 的结果来看，当企业在市场上的设施数低于竞争对手时，企业应选择较低的价格以吸引尽可能多的顾客，提高总体利润，当企业在市场上的设施数大于竞争对手时，企业在市场占有率上已有先天优势，应适当提高其产品售价，以使总体利润最大。

5 结论

新的企业的进入必然打破市场上原有的平衡，并影响市场上已存在的企业的利润。处于资金等因素的限制，先进入市场的企业在无法对其设施位置进行调整的情况下，为了追逐利润的最大化，必然对其产品价格进行调整。本文以此为背景，通过构造效用函数，引入Huff模型，提出了竞争环境下截流问题的选址-价格模型，证明了双方纳什均衡解的存在性和唯一性，构造启发式算法对模型进行求解，并将启发式算法的计算结果与枚举算法的计算结果进行了比较，证明了本文所提算法的有效性。下一步，我们将对消费者具有多种需求情况下的选址问题进行研究。

[1] Saidani N, Chu F, Chen H X. Competitive facility location and design with reactions of competitors already in the market[J]. European Journal of Operational Research, 2012, 219: 9-17.

[2] Hotelling H. Stability in competition[J]. The Economic Journal, 1929, 39(153): 41-57.

[3] Hoover E M. Spatial price discrimination[J]. The Review of Economic Studies, 1937, 4(3): 182-191.

[4] Garcia M D,Pelegrin B P,Fernandez P. Location strategy for a firm under competitive delivered prices[J]. The Annals of Regional Science, 2011, 47: 1-23.

[5] Serra D, Revelle C. Competitive location and pricing on networks[J]. Geographical Analysis, 1999, 31(1): 109-129.

[6] Perez M D G,Hernandez P F,Pelegrin B P. On price competition in location-price models with spatially separated markets[J]. Top, 2004, 12(2): 351-374.

[7] Aboolian R, Berman O, Krass D. Optimizing pricing an location decisions for competitive service facilities charging uniform price[J]. Journal of Operational Research Society, 2008, 59: 1506-1519.

[8] Pelegrin B,Fernandez P,Perez M D G. On the location of new facilities for chain expansion under delivered pricing[J]. Omega, 2012,40: 149-158.

[9] Hodgson M J. A flow-capturing location-allocation model[J]. Geographical Analysis, 1990, 22: 270-279.

[10] Berman O, Larson R C, Fouska N. Optimal location of discretionary service facilities[J]. Transportation Science, 1992, 26:201-211.

[11] Berman O, Krass D. Flow intercepting spatial interaction model: a new approach to optimal location of competitive facilities[J], Location Science, 1998, 6:41- 65.

[12] Wu T H, Lin J N. Solving the competitive discretionary service facility location problem[J]. European Journal of Operational Research, 2003, 144: 366-378.

[13] 杨珺，张敏，陈新.一类带服务半径的服务站截流选址-分配问题[J].系统工程理论与实践,2006,26(1):117-122.

[14] 胡丹丹，杨超.在竞争环境中的拥塞设施截流选址问题[J].系统工程理论与实践，2010,30(1)：68-72.

[15] Zeng, W, Castillo I, Hodgson M J. A generalized model for locating facilities on a network with flow-based demand[J]. Networks and Spatial Economics, 2010, 10: 579- 611.

[16] Zeng W, Hodgson M J, Castillo I. The pickup problem: consumers’ locational preferences in flow interception[J]. Geographical Analysis, 2009, 41: 107-126.

[17] Tanak K, Furuta T. A hierarchical flow capturing location problem with demand attraction based on facility size, and its lagrangian relaxation solution method[J]. Geographical Analysis, 2012, 44:15-28.

[18] 罗伯特·吉本斯著，高峰译.博弈论基础[M].北京：中国社会科学出版社，1999.

[19] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simulated annealing[J]. Science, 1983, 220: 671- 680.

[20] Al-eraidah O, Krishnamurthy A, Malmbrog C J. A two-stage simulated annealing procedure for block layout problems[J]. International Journal of Production Research, 2006, 44(20): 4417- 4429

Optimizing Location and Pricing Policies in Competitive Flow Interception Problem

SHENG Rui-ling1, HUO Jia-zhen2, WANG Qian3

(1.SchoolofMathematicsandInformationScience,HenanUniversityofEconomicsandLaw,Zhengzhou450000,China; 2.SchoolofEconomicsandManagement,TongjiUniversity,Shanghai200092,China; 3.HenanUniversityofTechnology,Zhengzhou450000,China)

We present the model of optimizing the location and pricing for a firm entering a competitive market in a flow interception problem. The entering firm charges uniform mill price and aims at finding the locations and price to optimize its overall profit. The competitor, on the other hand, can react by adjusting its price with the objective of maximizing its own profit. We define the utility functions, and a probability of customers on each path patronizing the facility is described by a Huff-like model. A heuristic algorithm is presented. We also analyze the benefit of the entering firm gains considering the competitor’s reaction.

operations research; flow-interception facility location; location-pricing; Nash equilibrium; simulated annealing algorithm

2013- 06- 20

国家自然基金资助项目(71102071,71002020，11371122)；国家自然科学基金重大项目资助(71090404/71090400)；河南省社科规划基金资助项目(2014BZHD10)

申瑞玲，女，河南长葛人，博士研究生，研究方向：运营管理，设施选址；霍佳震，男，安徽芜湖人，博士，教授，博士生导师，研究方向：运营管理，供应链管理；王茜，女，河南郑州人，博士研究生，研究方向：企业管理。

O221.2

A

1007-3221(2015)04- 0122- 06