基于产品合格率随机分布的投产量模型优化

张毕西， 谢祥添,2

(1.广东工业大学 管理学院,广东 广州 510520； 2.广东理工职业学院 管理工程系,广东 广州 510091)



基于产品合格率随机分布的投产量模型优化

张毕西1， 谢祥添1,2

(1.广东工业大学 管理学院,广东 广州 510520； 2.广东理工职业学院 管理工程系,广东 广州 510091)

当产品合格率随机分布时，建立起以投产综合损失费(欠产再投产费，过量产出费和不合格处理费)期望值为目标函数，投产量为决策变量的投产量模型。结合产品合格率随机分布不同(均匀分布和正态分布)推导求解了模型的最优解，得出了产量与投产量的等式关系，据此可有效地指导生产。最后通过数值实例分析验证了模型的有效性。

订单式生产；投产量；产品合格率；误差函数；欧米加函数

0 引言

在以客户为中心的市场经济中，许多企业采用了多品种、小批量、订单式的生产方式[1]。在这种生产方式过程中，由于品种多样，经常调整生产设备和生产批量小，相对于大批量、标准化生产模式，产品合格品率较低，若仍以产品的实际产量作为投产量，会导致欠产而重复投产，致使成本升高和交货期难以保证；过量生产又会导致生产过剩而产生过量处理费用。在订单式生产过程中，订单中有一小部分产品是新产品或者重复生产低[2]，这类产品的合格率能够预测为一定的范围内出现，因而可以建立产品合格率服从均匀分布的投产模型。对于大部分产品的合格率在生产过程中受到大量独立的随机因素如原材料、设备、人员、环境等的影响，根据中心极限定理它往往近似地服从正态分布[3]。文献[4]研究了产品的合格率服从正态分布，以损失期望值最小化为目标，建立了产品计划投产量优化决策模型，并针对某生产企业的生产问题，建立了投产决策离散模型很好解决了该企业投产量的实际问题，但是该文并没有给出投产决策模型数学意义上的最优解。本文在投产决策模型的基础上，通过费马定理和极值第二充分条件推导求解了产品合格率分别服从均匀分布与正态分布时的最优解，得出了投产量与产量之间的等式关系，这对企业投产计划量有一定的指导作用。

1 投产量模型

模型参数：

过量产出的损失费期望值为：

(1)

s.t.riPi≥Qi

产量不足的损失费期望值为：

(2)

s.t.riPi≤Qi

以投产综合损失费期望值为投产量决策标准，产品i投产量决策模型如下：

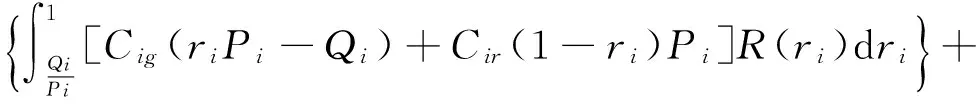
(3)

s.t.Pi≥0, 0≤ri≤1

2 ri～U(a,b)模型优化

若产品i的合格率ri～U(a,b)则有：

(4)

把式(4)代入式(3)有：

(5)

(6)

对含未知数Pi的方程(6)求解得：

(7)

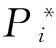
3 ri～N(u,σ2)模型优化

3.1 产品i的合格率ri～N(0,12)模型求解

若产品i的合格率ri～N(0,12)则有：

(8)

把式(8)代入式(3)有：

(9)

式(9)中有两种类型的积分：

(1)在积分函数中标准正态概率函数系数含ri的，设该类型积分为f1：

(10)

(2)在积分函数中标准正态概率函数系数不含ri的，设该类型积分为f2：

(11)

其中b，a是积分的上下限；λ是系数；erf(x)函数为误差函数，表达式为[5]：

(12)

根据式(10)和(11)可求式(9)化简有：

(13)

(14)

其中误差函数erf(x)的导数为[5]：

(15)

t1ep+t2+t3pep=0

(16)

其中t1，t2和t3是系数，方程(16)的求解过程如下：

设：t1+t3p=z，所以p=(z-t1)/t3

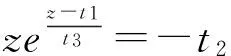
(17)

其中LambertW为欧米加函数或乘数对数其表达式为[6]：

LambertW(x)eLambertW(x)=x

(18)

根据式(17)可得方程(14)的解为：

(19)

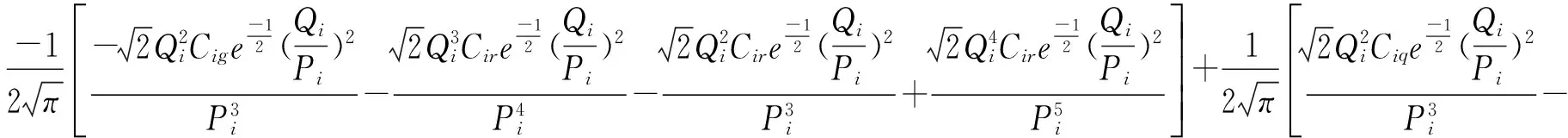
(20)

现设

(21)

在实数范围内LambertW(x)有两个分支，其中主分支，当x∈[-1/e,+∞)时，LambertW(x)>-1[6,7]，其图像如图1所示。

图1 LambertW(x)实数范围主分支

3.2 产品合格率ri～N(u,σ2)模型求解

若产品合格率ri～N(u,σ2)则有：

(22)

把式(22)代入式(3)有：

(23)

(24)

其中式(23)同样有两种类型的积分：

对式(23)E(Pi)″化简有：

(25)

4 数值实例

产品1：

根据模型参数的定义有：S1=3000元/次，Q1=3000kg，C1r=120元/kg，C1q=180元/kg，C1g=260元/kg，r1～U(0.70,0.98)和Pi=P1，把它们分别代入式(5)有：

(26)

对上式作E(P1)与P1的关系图，如图2所示。期望成本E(P1)随着P1的增加先下降后增加，存在一个最小值。

把S1=3000元/次，Q1=3000kg，C1r=120元/kg，C1q=180元/kg，C1g=260元/kg和r1～U(0.70,0.98)分别代入式(7)的Pi1有：

图2 E(P1)与P1的关系(r1～U(0.70,0.98)) 图3 E(P2)与P2的关系(r2～N(0.9,12))

产品2：

根据模型参数的定义有：S2=3500元/次，Q2=5000kg，C2r=120元/kg，C2q=180元/kg，C2g=260元/kg，r2～N(0.9,12)和Pi=P2，把它们分别代入式(23)有：

(27)

对上式作E(P2)与P2的关系图，如图3所示。期望成本E(P2)随着P2的增加先下降后增加，存在一个最小值。

把S2=3500元/次，Q2=5000kg，C2r=120元/kg，C2q=180元/kg，C2g=260元/kg，r2～N(0.9,12)和Pi=P2分别代入式(24)有：

5 结束语

(1)通过对产品合格率随机分布的投产量模型求解分析可知：当合格率服从均匀分布和标准正态分布时，存在着最优投产量使得产品的投产综合损失费最小。

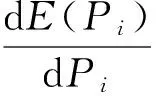
的根解将是我们研究的内容，其中t1，t2，t3，t4，t5和t6是系数。

[1] Stevenson M, Hendry L C, Kingsman B G. A review of production planning and control: the applicability of key concepts to the make-to-order industry[J]. International Journal of Production Research, 2005, 43(5): 869- 898.

[2] Mohd S M, Hendry L.The SHEN model for MTO SMEs: a performance improvement tool[J]. International Journal of Operations & Production Management, 2003, 23(5): 470- 486.

[3] Chatterji S D. Lindeberg’s central limit theorem à la Hausdorff[J]. Expositiones Mathematicae, 2007, 25(3): 215-233.

[4] 张毕西,宋静,关柳颖.基于订单式生产下的产品计划投产量决策[J].系统工程理论与实践,2008,7:165-168.

[5] Erdélyi A, Magnus W, Oberhettinger F, Bateman H. Higher transcendental functions[M]. McGraw-Hill: New York, 1953.

[6] Corless R M, Gonnet G H, Hare D E G, et al. On the lambertW function[J]. Advances in Computational Mathematics, 1996, 5(1): 329-359.

[7] 龙敏,周铁军.Lambert W函数性质及其应用[J].衡阳师范学院学报,2001,32(6):38- 40.

[8] Shampine L F, Kierzenka J, Reichelt M W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c[J]. Tutorial Notes, 2000, 6: 1-30.

[9] 吴专保.非线性方程几种数值解法的MATLAB程序[J].宁波职业技术学院学报,2007,11(2):20-22.

Optimizing the Model of Quantity Putting into Production Based on Product Pass Rate Randomly Distributed

ZHANG Bi-xi1, XIE Xiang-tian1,2

(1.SchoolofManagement,GuangdongUniversityofTechnology,Guangzhou510520，China; 2.DepartmentofManagementEngineering,GuangdongPolytechnicInstitute,Guangzhou510091,China)

When the product pass rate is randomly distributed, we build up the decision-making model of quantity putting into production, which is with total loss (insufficient production and then putting into production again charges, excess output charges and unqualified handling charges) expected value as the objective function, quantity putting into production as the decision variables. We sdve the optimal solution of the model with uniform distribution or normal distribution, and obtain equation between production and cast production, which effectively guide the production plan. Finally, we use a numerical example to prove the model is valid.

make to order; quantity putting into prodution; pass rate of product; erf(x); LambertW(x)

2013- 03-11

国家自然科学基金项目：适应复杂需求的SMPEs运营作业系统管理与优化研究(71271060)，订单式生产人工作业系统(MTO/MOS)组织与优化研究(70971026)； 广东省自然科学基金项目:复杂需求环境下小型制造企业作业系统组织与优化研究(S2012010009278)；广东理工职业学院资助项目: 基于复杂环境下中小型企业标准化生产运营系统优化研究(1321)。

张毕西(1954-)，男，教授，博士生导师，主要研究方向：生产系统优化、供应链管理。谢祥添(1981-)，男，博士，讲师，主要研究方向：管理科学与工程。

F2

A

1007-3221(2015)04- 0097- 08