基于满意度函数的多响应稳健优化模型及实证研究
2015-07-07刘玉敏赵利肖
刘玉敏, 赵利肖
(郑州大学 商学院, 河南 郑州 450001)
基于满意度函数的多响应稳健优化模型及实证研究
刘玉敏, 赵利肖
(郑州大学 商学院, 河南 郑州 450001)
针对传统的综合满意度模型在研究多响应时较少考虑噪声因素的问题,本文通过引入噪声因素对传统的满意度模型实施改进,进行多响应稳健优化分析。首先,构建包含可控因素和噪声因素的多质量特性的响应曲面模型;其次,借助传统综合满意度模型的构建方法,将多质量特性的响应曲面模型整合为改进的满意度模型;最后,将信噪比作为衡量改进的满意度模型稳健优化的指标,得到稳健优化的参数组合。实证研究表明:构建同时包含可控因素和噪声因素的改进的满意度模型是可行的,在此模型的基础上利用信噪比能够有效地找到多响应稳健优化的参数组合。
质量管理 ;包含噪声因素的满意度模型;响应曲面法;满意度函数法;信噪比分析;多响应;稳健优化
0 引言
多响应稳健优化的研究在优化多个响应值的同时提升了质量特性的稳健性,不仅可以帮助企业提升产品的质量,同时可以满足顾客多样化的需求。近年来,国内外学者研究多响应稳健优化问题的一般思路为,首先建立多质量特性的单一响应函数,其次基于满意度函数进行转换,最后得到综合满意度模型后再确定可行解。Kim和Lin通过构建所有响应的位置模型μ和散度模型σ,并借助满意度函数的理念,建立μ和σ的综合满意度函数,该综合满意度函数只包含了可控因素与满意度之间的关系,其实质是对双响应曲面的应用[1]。Amirhossein 和Mahdi等学者通过构造多元过程能力指数对非正态的多响应稳健优化进行了研究[2]。S. Pourzeynali等在研究多响应稳健优化时,运用了遗传算法。同时,为了营造稳健优化的过程使用了哈默斯利序列取样法[3]。我国学者何祯等将置信区间作为衡量稳健性的指标,通过构建多个响应与可控因素之间的函数,对多响应稳健优化进行研究[4]。
综上所述,在构建传统的综合满意度模型时只考虑了可控因素,忽视了噪声因素,在构造单一响应函数时,研究的仅仅是可控因素和响应之间的关系[5,6]。同时,在对多响应进行稳健优化时,衡量稳健性的指标是不同的。理想的稳健性指标应该同时包括反映设计目标均值的μ和反映离散程度的方差σ。
因此,本文将噪声因素引入到综合满意度模型的构建中,提出了改进的满意度模型,并以此为目标模型,借助信噪比的稳健优化理念,找到了多响应稳健优化的参数组合。首先,基于响应曲面法,建立同时包含可控因素和噪声因素的多质量特性的单一响应模型。其次,借鉴传统的满意度函数转化方法,将多个单一响应函数转化为[0,1]区间上的单一满意度函数,根据加权几何平均法构建改进的满意度模型,以此作为多响应稳健优化的模型。再次,用信噪比对改进的满意度模型进行稳健性分析,结合灵敏度,得到稳健优化的参数组合,实现了优化多响应的同时使其具备稳健性。最后,以A公司某焊接过程为例,运用该方法体系对焊接过程的三个响应进行稳健优化,研究结果表明:引入噪声因素的改进的满意度模型是可以被有效构建的,并且以信噪比为稳健性衡量指标,是能够得到更理想的参数组合的。
1 改进的多响应模型
传统的综合满意度模型在解决多响应问题时,没有考虑噪声因素,仅研究了可控因素和响应之间的关系。同时,质量特性的响应函数是构建满意度模型的基础。基于此,结合响应曲面法,构造同时包含可控因素和噪声因素的多质量特性单一响应模型,并借鉴传统的综合满意度模型的构建方法,得到改进的满意度模型,即改进的多响应模型D=f(x,z),该模型与传统综合满意度模型D=f(x)的区别在于,是否引入噪声因素。
1.1 单一响应模型
传统的响应曲面法(RSM)在拟合响应函数时,只考虑了可控因素与响应之间的关系[7]。虽然最终的拟合函数充分满足了质量特性的目标值μ,却忽视了质量特性的波动σ,即忽略了质量特性的稳健性。不仅如此,为了在改进的满意度模型的基础上研究多响应稳健优化,构建同时包含可控因素和噪声因素的质量特性的响应函数y=f(x,z)是必要的。
假设在多响应的研究中,有n个需要进行稳健优化的关键质量特性,m个可控因素和k个噪声因素。噪声因素在生产中是不可控的,但是在实验中必须是可控的。模拟的噪声因素个数越多越好,但是由于经济性要求以及一些噪声因素在实验环境下也无法做到控制,没有必要对所有的噪声因素进行研究,只需要在不同的噪声因素中各取一个重要的即可,本文选择三个噪声因素,分别代表内干扰、外干扰、产品间干扰,即k=3。
借助传统的响应曲面函数的构建方法,在实验设计阶段引入噪声因素,绘制(m+3)因子实验表,然后按照因子实验表中的试验组合进行试验,收集到n个质量特性值,在Minitab软件中进行统计分析。响应曲面模型的构建通常需要两个步骤:
(1)如果统计分析结果显示曲率不显著(p>0.05),说明一阶模型已经可以真实地反映响应与变量之间的关系,模型拟合得很好。
不包含交互作用的一阶函数:
(1)
包含交互作用的一阶函数,交互作用项不仅包括可控因素之间的交互作用,同时也包括可控因素与噪声因素之间的交互作用。
(2)
(2)如果统计分析结果显示部分或全部质量特性yi的曲率显著(p<0.05),那么部分或全部一阶函数模型已经不能够真实地反映响应与变量之间的关系,拟合二阶函数模型是必要的。从形式上看,二阶响应曲面模型比一阶模型增添了自变量的平方项。由于RSM法具备“序贯性”的优点,在进行二阶模型的拟合时,不需要重新设计大量的试验进行数据收集,只需要利用CCD(中心复合设计)或者Box-Behnken等设计方法,在一阶模型的数据上再增加补充一些试验点即可,这些补充的试验点的水平组合借助Minitab软件进行设计,然后在新的试验点上进行试验。
增加试验点后,重新拟合的二阶函数关系式如下:
(3)
其中,ε是实验结果与实际结果之间的误差项,β0i表示常数项,βij是自变量与因变量之间的系数。
在筛选二阶平方项时,可不考虑噪声因素的二阶平方项。如果曲率的存在是由噪声因素的平方项引起的或者噪声因素的平方项对曲率影响显著的话,该质量特性响应的变化在很大程度上依赖于外界噪声因素的变化,此时的二阶模型也是没有意义的。
综合使用上述两个步骤(1)、(2),得到多质量特性的单一响应曲面模型见公式(1)~(3),该模型同时包含可控因素和噪声因素。
1.2 多响应模型
满意度函数法能够有效地将多响应转化为单一响应,然而传统的综合满意度模型没有考虑噪声因素。基于(1)~(3)中得到的单一响应曲面函数,构建包含噪声因素的多响应模型——改进的满意度模型。
1.2.1 单一响应满意度函数
单一满意度函数是构建综合满意度函数的基础,根据Derringer和Suich定义的单一满意度函数的形式[8~12],将公式(1)~(3)中的单一响应函数yi转化为[0,1]区间的单一满意度函数di。
假设:n个响应函数yi中,y1……yp质量特性的目标为望目;yp+1……yq质量特性的目标是望大;yq+1……yn质量特性的目标是望小。其中,n>q>p。
首先,结合实际需要,规定不同类型的质量特性y的目标值范围。当质量特性为望目时,Li≤yi≤Ui,其中yi的目标值设定为Ti;当质量特性为望大时,规定该质量特性值的下限Li及其可以达到的最大值;当质量特性为望小时,确定该质量特性的上限Ui及其可以达到的最小值。将公式(1)~(3)代入到Derringer和Suich定义的单一满意度函数中,得到包括噪声因素的单一满意度函数(4)~(6)。
(1)y1……yp质量特性的目标为望目,单一满意度函数如下:
(4)
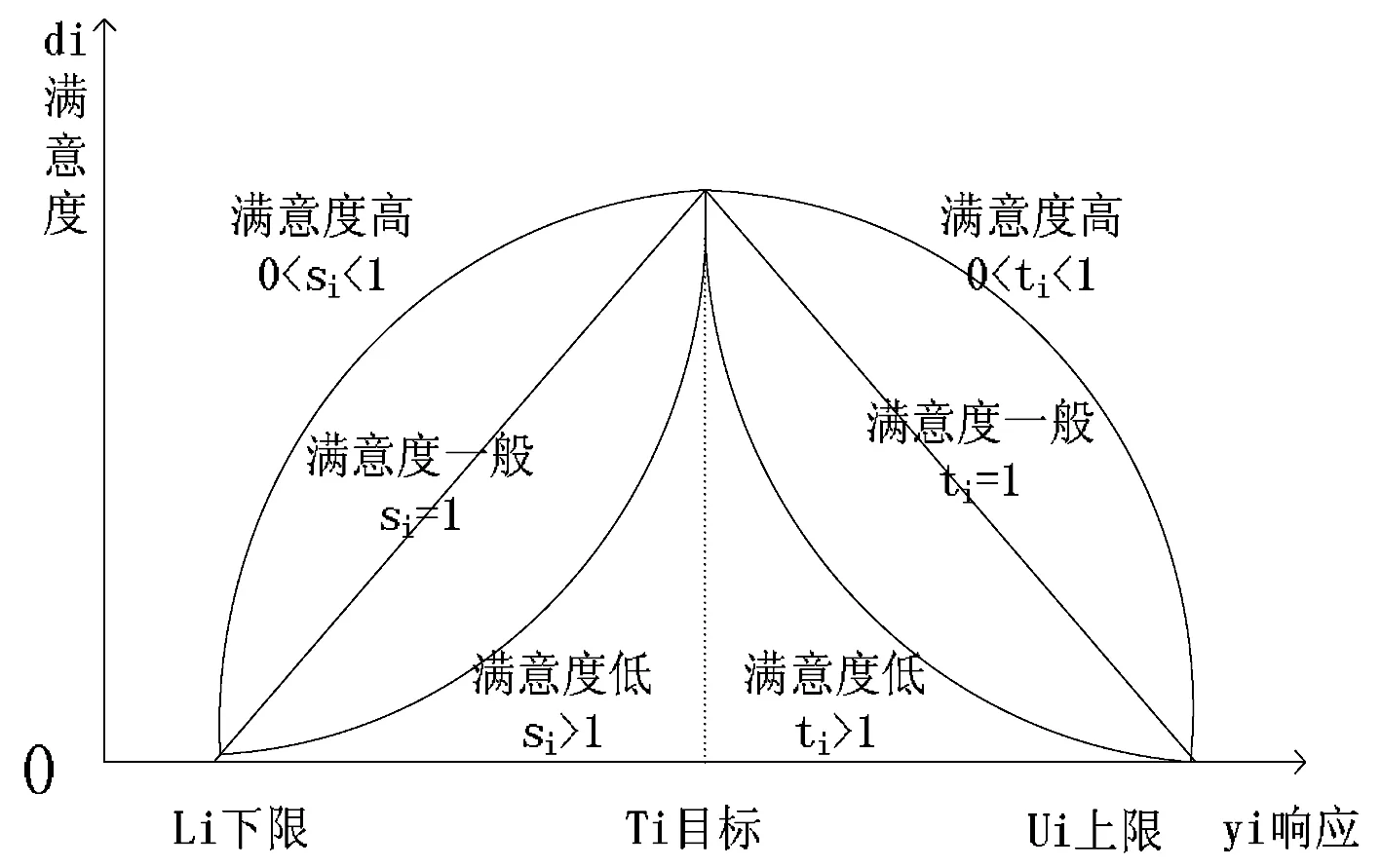
图1 质量特性的目标为望目时 的满意度函数图
望目特性的满意度函数的图形,如图1所示。
Li,Ui是响应y的下限和上限,Ti是响应y的目标值。当产品的质量特性为望目时,响应y可以从双边向目标值靠拢,且距离目标值越近,满意度最大,0≤di≤1。si,ti(s,t>0)反映了目标值被满足的过程中,带来的满意度的大小。同时,si,ti的大小决定了单个满意度函数的形状,比如凹凸性或者是线性。当si=1或ti=1时,满意度函数di为线性曲线,在y值从两边向目标值靠拢的过程中,满意度一般;当0
(2)yp+1……yq质量特性的目标为望大,单一满意度函数如下:
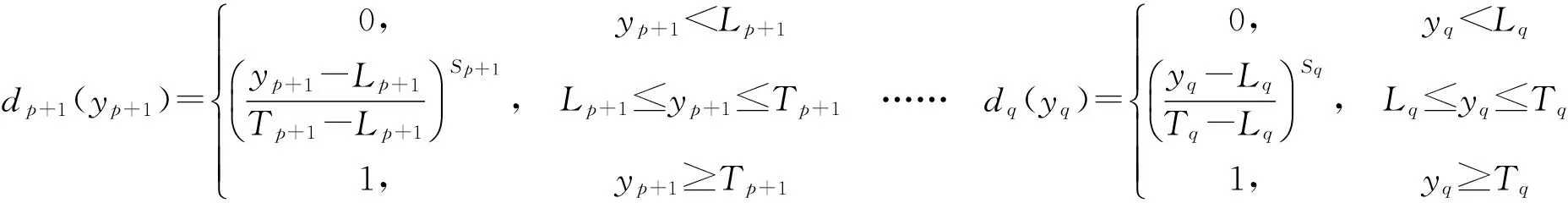
(5)
望大特性的满意度函数的图形,如图2所示。
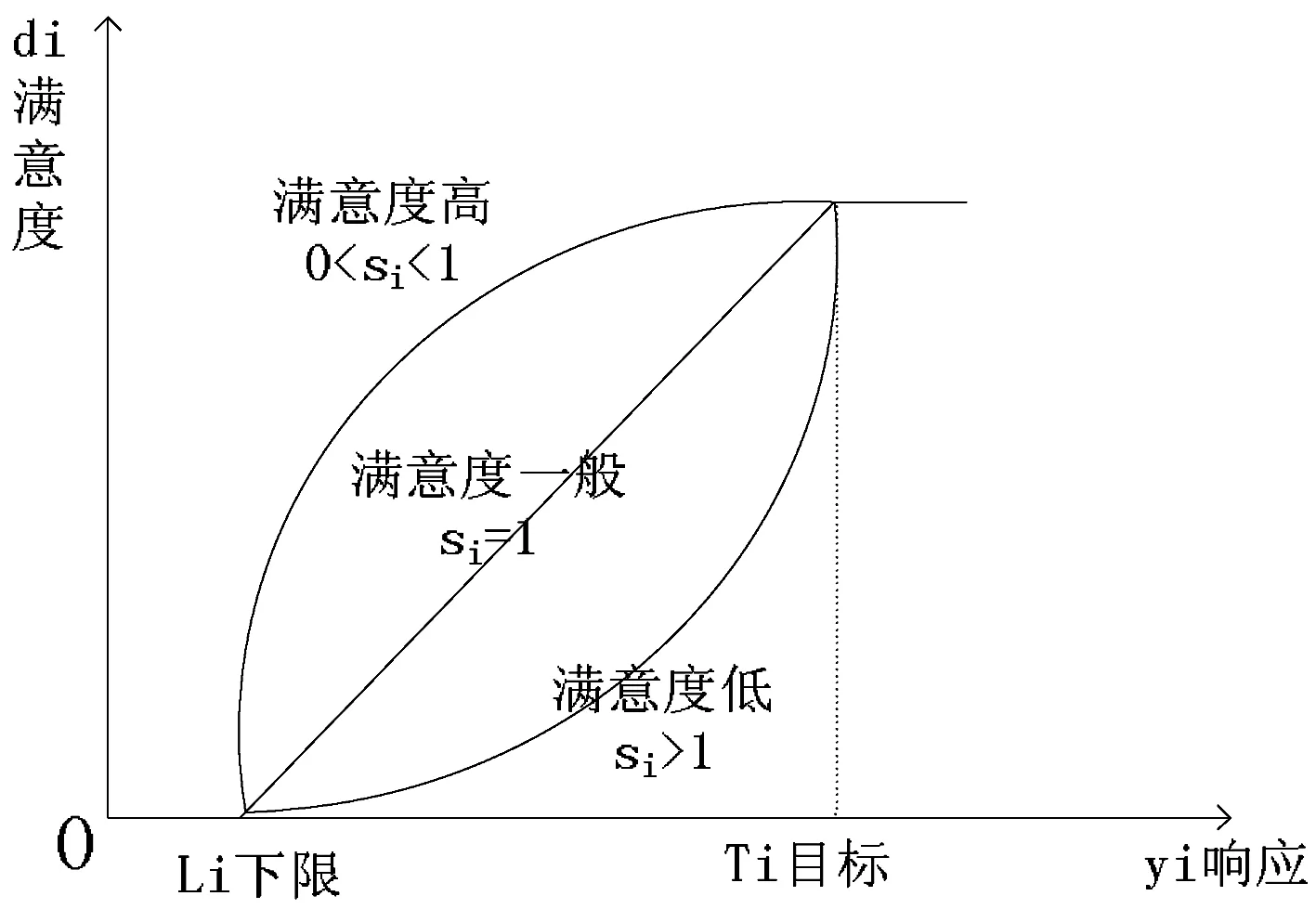
图2 质量特性的目标为望大时的满意度函数图
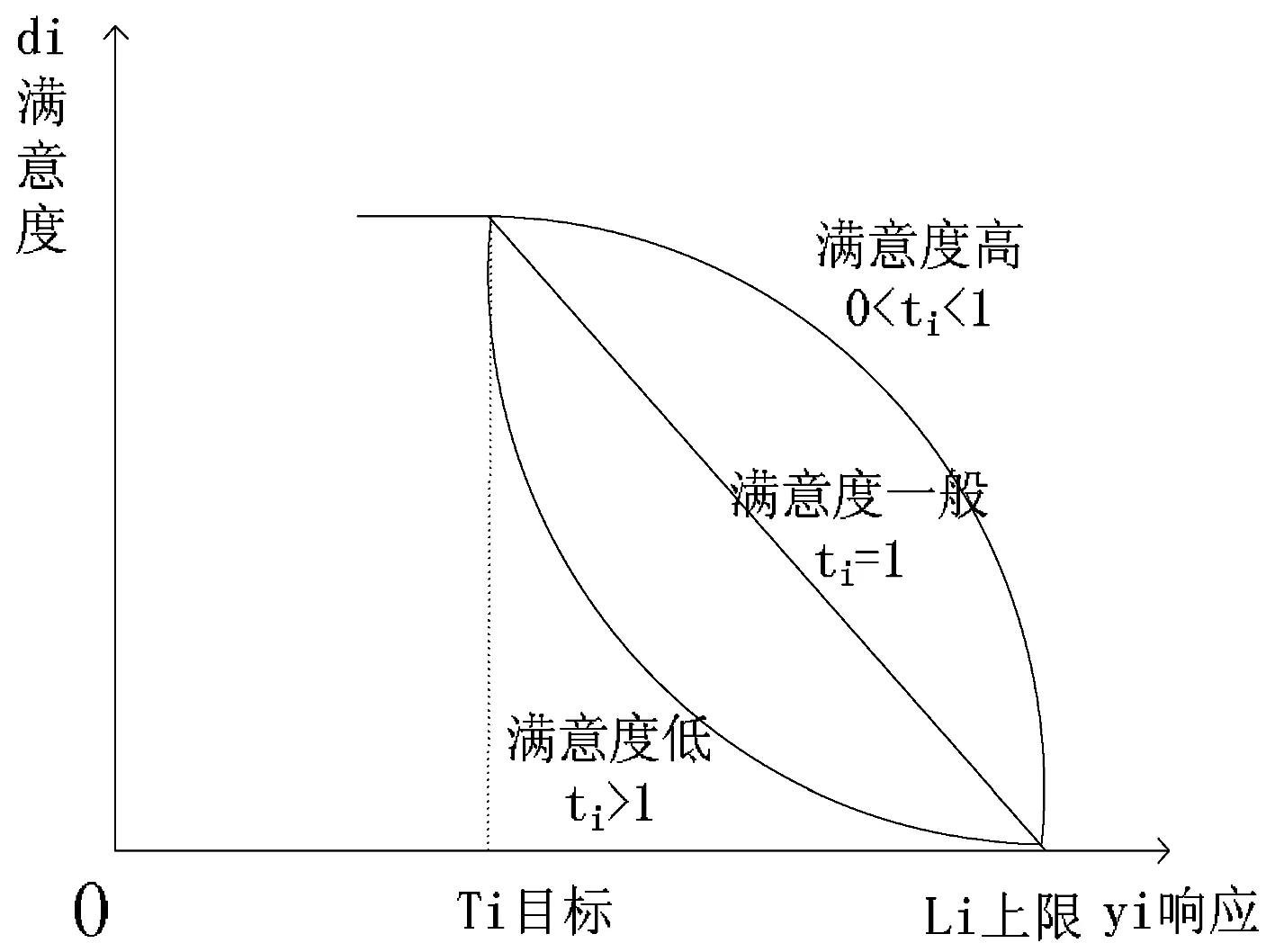
图3 质量特性的目标为望小时的满意度函数图
Ti表示响应y值在实际中可以达到的最大值ymax。当产品的质量特性为望大时,响应y值越大,满意度越高。si(si>0)表示响应y值从下限Li向最大值Ti靠近的过程中,带来的满意度。0
(3)yq+1……yn的的质量特性为望小,单一满意度函数如下;
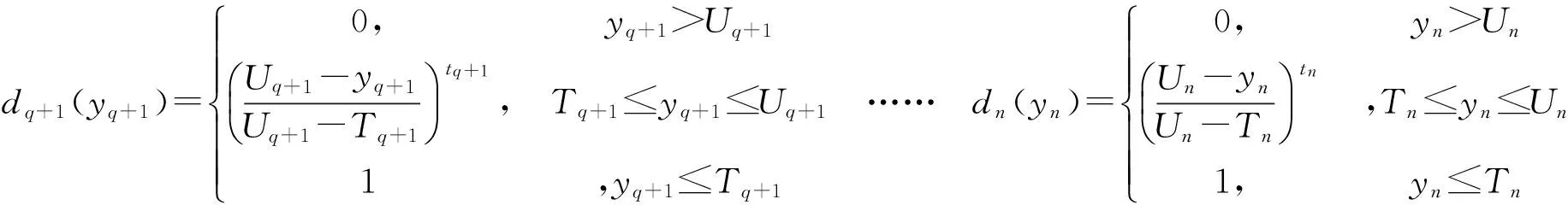
(6)
望小特性的满意度函数的图形,如图3所示。
Ti表示响应y值在实际中可以达到的最小值ymin。当产品的质量特性为望小时,响应y值越小,满意度越高。ti(ti>0)表示响应y值从上限Ui向最小值Ti靠近的过程中,带来的满意度。0
1.2.2 改进的满意度模型
满意度函数法的核心思想是将多响应转化为单一响应,目的是能够同时研究多个响应。将单一响应转化为单一满意度函数di之后,采用几何加权平均的方法构建改进的满意度模型D(x,z)。
首先,根据实验条件和工程需求对每个质量特性的满意度的权重进行赋值,更期望哪个质量特性得到优化,就赋予其较大的权重,反之赋予较小的权重,假设n个质量特性的权重分别设为w1,w2,…wp;wp+1,wp+2,…wq;wq+1,wq+2,…wn,采用几何加权平均法,传统的综合满意度模型为:
(7)
将公式(4)~(6)代入公式(7)中,得到反映可控因素和噪声因素的改进的满意度模型D(di):
D(di)=f(di)(x,z) (0≤D≤1)
(8)
公式(8)中改进的满意度模型D(di)是关于可控因素x和噪声因素z的函数,是对n个单一质量特性拟合函数y的整合,反映了在噪声因素z的影响下,多响应的总体满意度。同单一满意度的值域一样,D的取值也位于[0,1]内,且当D=1时,满意度最高。改进的满意度D值大小的稳健性可以直接反映多响应稳健优化结果的优劣程度,即当D=1,且D值不会随着噪声因素的波动而波动时,D值大小是稳健的,进而参数组合是理想的。
2 模型的稳健优化
信噪比作为衡量单一响应的稳健性指标被运用在各个领域[13,14],却很少结合满意度函数法在多响应的稳健优化得到运用。基于此,在改进的满意度模型D(di)中,将信噪比作为衡量改进满意度模型的稳健性指标,获取稳健优化的参数组合。
2.1 信噪比
改进的满意度模型D(di)的质量特性目标为望目,设目标值Ti为1。其信噪比的计算方法见公式(9)、(10)。其中,sm,ve,是关于可控因素和噪声因素的函数。
(9)
实际计算中,对η取对数,再乘以10,化为分贝值(dB)。
(10)
公式(9)、(10)中,信噪比的计算需要收集大量关于D的数据。假设,m个可控因素x和3个噪声因素z的中心值各有三个,为了准确估计结果,理论上需要做3m+3次试验。鉴于经济及时间的局限,采用正交表进行数据收集,记录结果见表1。
表1 改进的满意度模型优化方案表
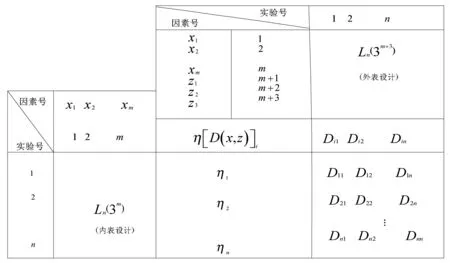
表1中,m个可控因素x有3个中心值,可以选择Ln(3m)型的正交表,得到内表中的n组实验方案。为了模拟出存在噪声因素的实验环境,需要对内表中的每一个方案进行外表设计,可以选择Ln(3m+3)型的正交表作为外表。内表中的每一个方案需要n次试验,可以收集到n个D值。进而,内表中n个方案一共需要nn次试验,共收集到nn个D值。
公式(8)中,改进的满意度模型D(di)是关于(x,z)的函数,是关于可控因素x和噪声因素z的拟合函数,对D(di)的研究结果可以真实地反映多响应的结果。所以,根据(x,z)值的不同组合,可以直接计算出对应的D值。这也是改进的满意度模型D(di)的一个优点,避免后续大量的实验,只需要合理的确定可控因素x和噪声因素z的中心值,并利用多响应模型优化方案表,即可计算nn个D值。
2.2 方差分析
采用表1中的设计方案,结合公式(8)计算n个内表方案下对应的n组D值,再结合公式(9~10),得到n个信噪比η(D)。对信噪比进行方差分析,判断影响信噪比的显著因素。方差分析见表2。

表2 方差分析表
k表示因素的水平数,本文取三水平实验,k=3。
1) syrup ['sɪrəp] n. 玉米糖浆 2) drought [draʊt] n. 干旱 3) bandit ['bændɪt] n.强盗
2.3 稳健优化解
多响应的稳健优化同单一响应一样,在分析信噪比的同时需要分析灵敏度。同理,对灵敏度进行方差分析。根据各个因素的显著性,将可控因素分为三类,见表3。

表3 改进的满意度模型D(di)的因素分类表
稳定因素和调节因素的识别为多响应模型最终的稳健优化提供了基础。因为稳定因素针对波动σ,调节因素针对目标值U。
基于表3,假设改进的满意度模型最终得到的稳定因素集合为(x1、x3、…xm),调节因素的集合为(x2、x7…xm-1)。根据信噪比最大即最优法则,结合表1,计算稳定因素集合中的各个因素三个水平下的信噪比,并进行比较,找到最大的信噪比所对应的水平。见表4

表4 稳定因素的信噪比分析表
在表4中,各个稳定因素信噪比最大的组合为(η12、η33…ηm3),对应的各个稳定因素的水平组合为(x12、x33…xm3),即(因素x1的二水平,因素x3的三水平…因素xm的三水平)。
综上,改进的满意度模型的最终参数组合为(x12、x33…xm3)。
在最优参数组合(x12、x33…xm3)下计算改进的满意度函数值,判断其距离目标值1的程度,如果D值远离目标值1,利用调节因素(x2、x7…xm-1)进行调节。

图4 焊道形成过程图
3 实证研究
本文收集了A公司某焊接过程的相关数据,研究了4个可控因素电流(X1)、电压(X2)、焊接速度(X3)、送丝速度(X4)以及两个噪声因素焊接材料的间隙(Z1)、厚度(Z2)与3个响应熔宽(T-W)、堆高(T_H)、熔深(P)之间的关系。基于改进的满意度模型的稳健优化过程,找到了同时优化三个响应的稳健优化参数组合。焊接过程见图4(白色部分表示焊道形状)。

表5 因素规格表

表6 响应规格表
3.1 焊道的多响应模型
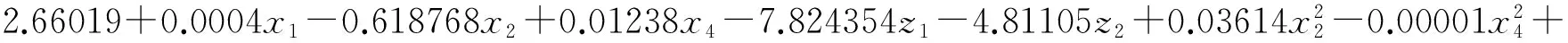
(11)
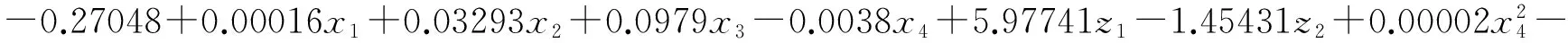
(12)

(13)
选择望目类型的满意度函数进行三个响应的转化。假设在向目标靠拢的过程中,满意度一般,取si=1,ti=1。熔宽、堆高、熔深的满意度函数见公式(14~16)。
(14)
(15)
(16)
将公式(11)~(13)代入公式(14)~(16),取w1,w2,w3都为1/3得到改进的满意度模型D,见公式(17)。
D={d1[f(T_W)]×d2[f(T_H)]×d3[f(p)]}1/3
(17)
3.2 焊道多响应模型的解
以信噪比为稳健性衡量标准,改进的满意度模型(公式17)为目标值,采用内外表直积法,绘制内外表直接方案,见表7。
表7 内外表直积方案汇总表
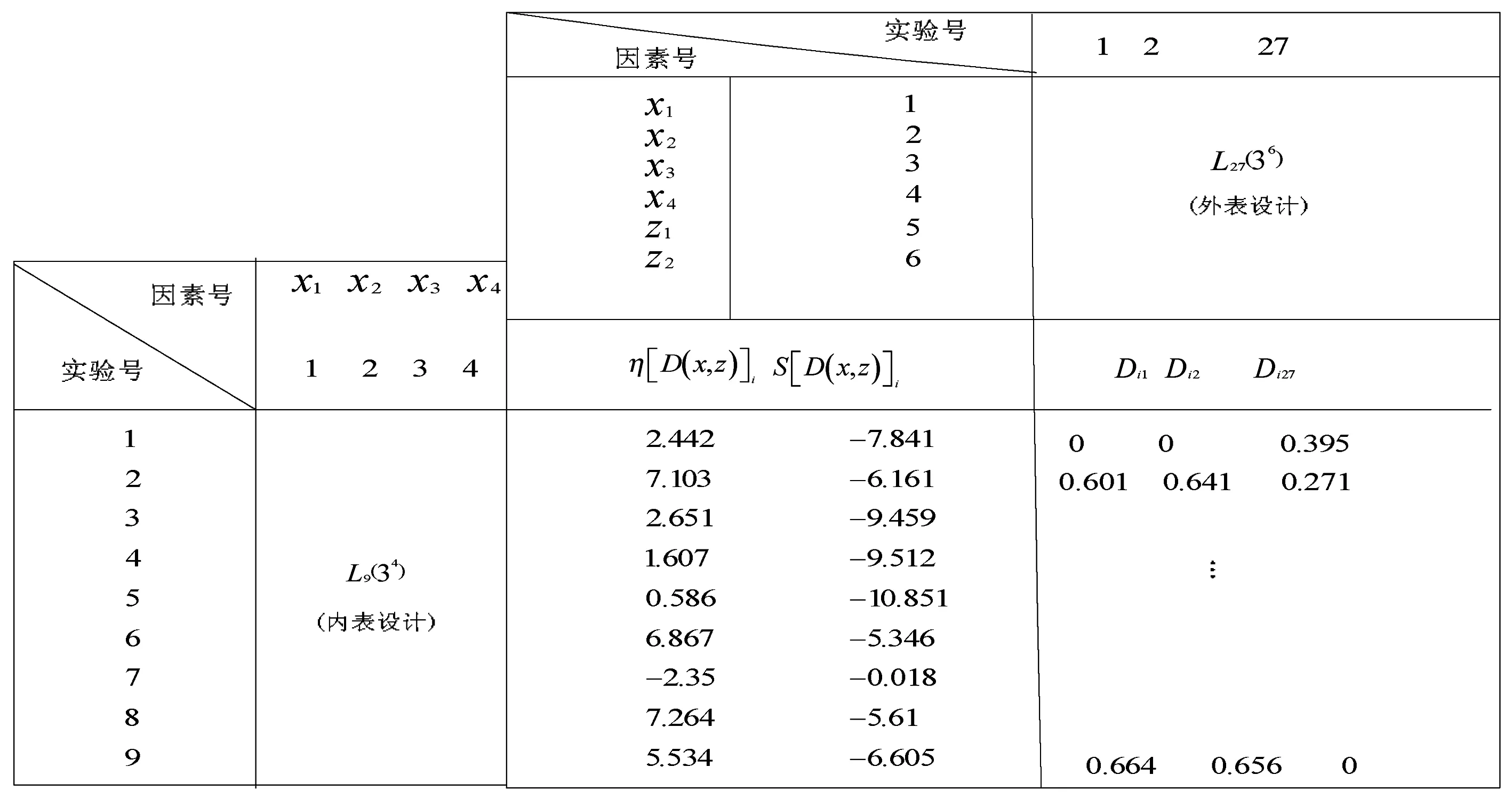
在表7中,对信噪比和灵敏度进行方差分析,因为可控因素较多,误差项不明显,所以将方差分析中平方和S最小的因素作为误差因素,进而将信噪比的方差分析中“电流”作为误差因素,灵敏度的方差分析中“焊接速度”作为误差因素。分析结果见表8~9(共得到9组实验数据,方差总自由度为9-1=8)

表8 焊道形成过程——信噪比的方差分析表

表9 焊道形成过程——灵敏度的方差分析表
结合表8和表9的信噪比和灵敏度的方差分析结果,对4个可控因素进行分类,见表10。

表10 因素分类表
表10中,电压、焊接速度为稳定因素,电流和送丝速度是调节因素,当最优水平组合下的响应没有达到目标值时,可以调整电流和送丝速度的水平。
表11中,电压的2水平和3水平的信噪比相差很小,可以将其最优水平定为2水平或3水平,焊接速度的水平定为1水平。电流和送丝速度的水平可以任意选,如C1V3T1W3,是稳定性最佳的设计方案。从表7中可以看出第8号方案下的信噪比最大,也可以选择C3V2T1W3为最优水平组合。

表11 因素的信噪比分析表
3.3 原方案与稳健优化方案统计特性的比较
原方案的参数组合为C1V1T1W1(128,7,5,72),基于改进的满意度模型的稳健优化的方案为C3V2T1W3(130,7.5,5,74),两个方案进行对比,(见表12)新方案的信噪比较大,稳健性强于原方案,而满意度的均值也比原方案更接近于目标值1,所以新方案是可行的。如果需要更高的满意度,可以调节电流C和送丝速度W这两个因素。

表12 原方案与优化方案对比表
4 结语
传统的综合满意度模型在解决多响应问题时较少考虑噪声因素,研究的仅仅是可控因素与响应之间的关系,基于此,本文将噪声因素引入到综合满意度模型的构建过程中,构建了包含可控因素和噪声因素的改进的满意度模型,在此基础上,将信噪比作为衡量改进的满意度模型的稳健优化的指标。本文重点介绍了改进的满意度模型的构建方法以及稳健优化的方法,以不同的视角为多响应稳健优化的解决提出了一套新的方法体系。对A公司焊接过程的实证研究表明:该方法体系能够得到比原方案更加稳健、更接近目标值的方案,改进的满意度函数在解决多响应稳健优化中是可行的。
[1] Kim K J, Lin D K J. Optimization of multiple response considering both location and dispersion effects[J]. European Journal of Operational Research, 2006, 169(1): 133-145.
[2] Amirhossein Amiri, Mahdi Bashiri, Hamed Mogouie, et al. Non-normal multi-response optimization by multivariate process capability index[J]. Scientia Iranica, 2012, 19(6): 1894-1905.
[3] Pourzeynali S, Salimi S, Eimani Kalesar H. Robust multi-objective optimization design of TMD control device to reduce tall building responses against earthquake excitations using genetic algorithms[J]. Scientia Iranica, 2013, 20(2): 207-221.
[4] He Zhen, Zhu Peng-Fei, Sung-Hyun Park. A robust desirability function method for multi-response surface optimization considering model uncertainty[J]. European Journal of Operational Research, 2012, 221(1): 241-247.
[5] Bezerra M A, Santelli R E. Response surface methodology(RSM)as a tool for optimization in analytical chemistry[J]. TALANTA, 2008, 75(5): 956-977.
[6] Stephan Morgenthalera, Martin M. Schumacherb. Robust analysis of a response surface design[J]. Chemometrics and Intelligent Laboratory Systems, 1999, 47(1): 127-141.
[7] Vasilios Sakkas A, Md Azharul Islam, Constantine Stalikas, et al. Photocatalytic degradation using design of experiments: a review and example of the Congo red degradation[J]. Journal of Hazardous Materials, 2010, 175: 33- 44.
[8] Goethals P L, Cho B R. Extending the desirability function to account for variability measures in univariate and multivariate response experiments[J]. Computers & Industrial Engineering, 2012, 62(2): 457- 468.
[9] Jeong, In-Jun, Kim, Kwang-Jae. An interactive desirability function method to multi-response optimization[J]European Journal of Operational Research, 2009, 195(2): 412- 426.
[10] 何桢,宗志宇,孔祥芬.改进的满意度函数法在多响应优化中的应用[J].天津大学学报,2006,39(9):1137-1140.
[11] Ful-Chiang Wu. Robust design of nonlinear multiple dynamic quality characteristics[J]. Computers and Industrial Engineering, 2009, 56(4): 1328-1332.
[12] Bezerra M A, Santelli R E. Response surface methodology(RSM)as a tool for optimization in analytical chemistry[J]. Talanta, 2008, 76(5): 965-977.
[13] 李强.基于三次设计理论的质量优化设计系统研究[D].辽宁:东北大学,2008.
[14] Bharti P K, Khan M I, Harbinder Singh. Taguchi’s off line method and Multivariate loss function approach for quality management and optimization of process parameters-areview[J]. International conference on modeling, optimization, and compting, 2010, 1298(10): 486- 491.
A Robust Optimization Model for Multi-Responses Based On Desirability Function Approach and the Empirical study
LIU Yu-min, ZHAO Li-xiao
(BusinessSchool,ZhengzhouUniversity,Zhengzhou, 450001,China)
As the traditional comprehensive desirability model considers less of niose factors in the study for multi-responses, noise factors have been introduced into the traditional comprehensive desirability model in the paper to improve the previous one for analyging robust optimization. Firstly, response surface models of the multiple quality characteristics including controlled factors and noised factors have been conducted; secondly, based on the traditional comprehensive desirability model, we integrate multiple quality characteristics of response surface models with the improved desirability model; finally, S/N ratio has been used as an indicator of measuring robustness and optimization for the improved desirability model. The empirical study shows that the improved desirability model can be effectively conducted and can find ideal parameter combination with the help of S/N ratio.
quality management; the desirability model adding the noise factors; RSM; the desirability function; S/N ratio analysis; multi-responses; robust optimization
2013-12-17
国家自然科学基金资助项目 (71272207)
刘玉敏(1956-)女,河南濮阳人,教授,博士生导师,研究方向:质量设计,质量智能诊断等;赵利肖(1988-)女,河南济源人,在读硕士研究生,研究方向:质量管理。
F253.3
A
1007-3221(2015)04- 0083- 09
