基于区间模糊数的多阶段冲突型大群体应急决策方法

徐选华， 蔡晨光， 陈晓红

(中南大学 商学院，湖南 长沙 410083)



基于区间模糊数的多阶段冲突型大群体应急决策方法

徐选华， 蔡晨光， 陈晓红

(中南大学 商学院，湖南 长沙 410083)

针对阶段权重未知且偏好信息表示为区间模糊数的多阶段大群体应急决策问题，提出一种新的群决策方法。首先给出了区间模糊数相似度公式，利用该公式对各阶段的专家偏好信息进行聚类；然后构建相对熵优化模型对聚集权重和阶段权重进行求解，得到整个决策过程的综合群体偏好，根据综合群体偏好对备选方案进行排序，确定最佳方案；最后通过算例对该方法的有效性和可行性进行验证。

应急管理；群决策；相对熵；区间模糊数；多阶段

0 引言

近年来，非常规突发事件在世界范围内频繁发生：2003年的SARS、2004年的印尼海啸以及2008年的汶川地震等。非常规突发事件通常没有现成的应急预案做参考，事件一旦发生，就要求应急专家根据事件的状态在短时间内做出合理的应急对策。在时间压力下，专家很难对事件的状态做出准确判断，往往以模糊数的形式来表达自己的偏好：如区间模糊数、三角模糊数、直觉模糊数等[1～3]。同其他类型的模糊数相比，区间模糊数凭借其直观、简洁、易于表达的优势在模糊决策活动中得到广泛地应用，因此也得到了国内外许多学者的关注[4～9]。文[4]利用不确定性算术平均算子进行对属性进行赋权；文[5]针对属性偏好表示为不同形式的群决策问题,提出了一种偏好信息的统一化方法；文[6～7]综合考虑主观权重和客观权重的基础上，以两者之间的偏差水平最小化为目标，建立优化模型对属性权重或专家权重进行求解。文[8～9]对传统的TOPSIS法进行改进，使其适用于区间型属性信息的决策排序活动。

应急决策往往涉及多个部门，参与应急决策的专家数量要远超于常规群决策活动，这也使得应急决策多具有大群体特征(通常将参与决策的专家人数在11名以上(含11名)的群决策活动定义为“大群体决策活动”[10])。在决策过程中，由于各个专家在决策方法、决策态度、知识背景等存在差异，专家之间便不可避免地出现“偏好冲突[11]”，另外，突发事件具有动态性，决策专家需要根据不同阶段下突发事件的状态给出相应决策值，因此应急决策多呈现出多阶段的特点。在解决多阶段群决策问题时，通常利用阶段权重将各阶段的群体偏好进行集结，形成综合群体偏好，再进行后续的决策活动[12～13]。应急事件状态的不稳定性使得各阶段的群体偏好并不完全一致，因此各阶段的群体偏好与综合群体偏好之间也存在“偏好冲突”，如何妥善处理两种类型的“偏好冲突”，对提高决策活动的效率、保证决策结果的有效性具有重要意义。当前的研究大多集中于具有单一时段、少数决策者参与(通常不超过5个)的决策问题，对于具有多阶段大群体特征的决策问题研究较少。基于此，本文针对阶段权重未知且专家偏好信息表示为区间模糊数的大群体应急决策问题提出一种新的决策方法。

首先给出了区间模糊数相似度公式，将其作为相聚度公式对各阶段的专家偏好进行聚类；分别以同一集合中所有聚集的阶段内偏好冲突水平最小化和所有阶段的综合偏好冲突水平最小化为目标，构建相对熵优化模型对聚集权重和阶段权重进行求解。利用聚集权重和阶段权重对各阶段的专家偏好进行集结，得到整个决策过程的综合群体偏好，根据综合群体偏好信息对决策方案进行排序，从而确定最佳方案。

1 区间模糊数的相似度

常见的模糊数相似度测度方法包括Hamming距离相似度、Hausdorff距离相似度、Cosine相似度、Jaccard相似度等[14]。根据区间模糊数的表达特点，在Jaccard相似度模型基础上，将两个区间模糊数之间的相似度定义如下：

定义1 设α=[αL,αU]和β=[βL,βU]为在实数集X上的两个区间模糊数，其中0≤αL≤αU，0≤βL≤βU，α和β的相似度为：

(1)

满足以下3个性质：(P1)有界性：0≤S(α,β)≤1；(P2)对称性：S(α,β)=S(β,α)；(P3)自反性：S(α,β)=1,ifα=β。

对性质(P1)进行证明：

证明 已知0≤αL，αU，βL，βU，0≤2·αL·βL≤(αL)2+(βL)2；0≤2·αU·βU≤(αU)2+(βU)2,有0≤2·αL·βL+2·αU·βU≤(αL)2+(βL)2+(αU)2+(βU)2,代入(1)式有：

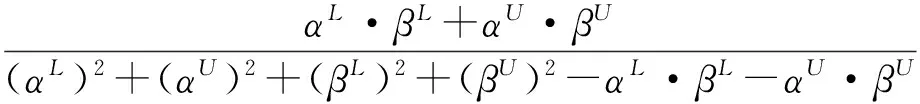
故性质(P1)成立。

易证性质(P2～P3)成立，在此不再赘述。

(2)

易证S(A,B)同样满足性质(P1～P3)，在此不再赘述。

2 方法原理

2.1 群体偏好聚类

(3)

(4)

2.2 聚集权重求解

(5)

在同一阶段下，将Cks的聚集偏好Gks与该阶段群体偏好Gs之间的偏差定义为该聚集的“阶段内偏好冲突”，利用相对熵模型对各个聚集的阶段内偏好冲突水平进行测度。第s个决策阶段下， 聚集Cks的阶段内偏好冲突为：

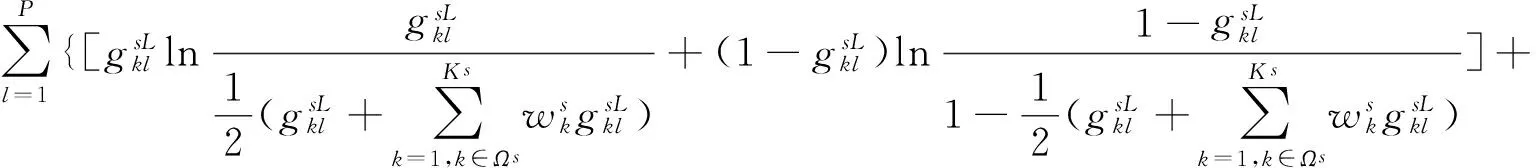
(6)

根据相对熵[16～18]的性质可知，聚集Cks的阶段内偏好冲突越小，εks的值越小。若εks=0,Cks的聚集偏好Gks与该阶段群体偏好Gs之间完全一致。以Ωs中所有聚集的阶段内偏好冲突水平最小化为目标构建相对熵优化模型，对第s个阶段的聚集权重进行求解。如式(7)所示。

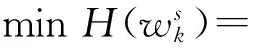
(7)

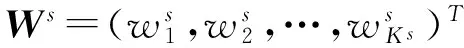
2.3 阶段权重求解

将聚集权重Ws代入式(5)，得到各个阶段的群体偏好Gs。设阶段权重为ω=(ω1,ω2,…,ωS)T，整个决策过程的综合群体偏好为：

(8)

将第s个阶段的群体偏好Gs与综合群体偏好G之间的偏差定义为该阶段的“综合偏好冲突”。利用相对熵模型对相应阶段的综合偏好冲突水平进行测度。第s个阶段的综合偏好冲突为：

(9)

同理,根据相对熵[16～18]的性质可知，第s个决策阶段的综合偏好冲突水平越小，ηs的值越小。当ηs=0时，群体偏好Gs与综合群体偏好G之间完全一致。以所有阶段的综合偏好冲突水平最小化为目标，对阶段权重进行求解。如式(10)所示。

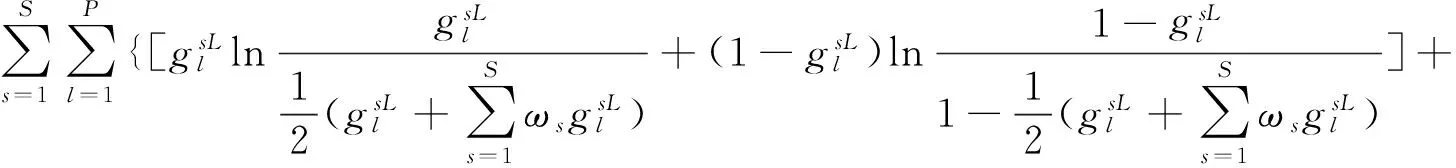
(10)

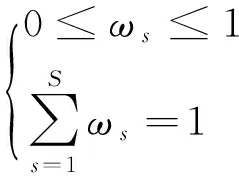
利用式(10)求得阶段权重ω=(ω1,ω2,…,ωS)T。

式(7)和式(10)可以利用MATLAB软件编程进行求解。

综上所述,给出的决策方法具体步骤如下：

Step 1 将专家偏好信息进行标准化处理，得到标准化后的专家偏好；

Step 2 以式(2)作为相聚度测度公式，对各个阶段的专家偏好矢量进行聚类；

Step 3 利用式(7)对不同阶段的聚集权重进行求解，根据式(5)得到各阶段的群体偏好；

Step 4 利用式(10)对阶段权重进行求解，根据式(8)得到整个决策过程的综合群体偏好；

Step 5 根据综合群体偏好信息对备选方案的偏好信息进行两两比较，构建偏好可能度矩阵Q=(qlf)p×p[19]。其中，qlf表示决策群体对于备选方案l的偏好大于备选方案f的概率，l,f=1,2,…,P,利用式(11)得到备选方案的排序向量O=(O1,O2,…,OP)[19]，选择最优方案。

(11)

3 算例分析

某地区公路沿线森林发生火灾，当公路沿线森林火灾发生时，一方面需要对火势进行控制，减少林木的毁坏，保障沿线村落的安全，另一方面需要尽量减小火灾对于交通基础设施和交通秩序的影响。综合上述救灾目标，应急部门制定了3种备选方案：(1)完全封闭公路，引入大型机械进行灭火，不疏散沿线村落居民；(2)封闭公路部分车道，引入小型机械进行灭火，疏散沿线村落居民；(3)不封闭车道，引入人工方式进行灭火，疏散沿线村落村民。大型机械的灭火效果最好，但需要大型的场地进行作业，因此需要对公路进行完全封闭；小型机械的灭火效果次之，仅需要较小的场地进行作业，仅需要封闭部分车道；人工方式灭火的效果较差，但不需要作业场地，具有灵活性和机动性。

对于森林火灾而言，风势、风向、地理位置和降雨等环境因素将会使火势产生阶段性变化，这也使得应急活动呈现出多阶段特点。通过对当前火情以及环境因素的分析，整个应急活动预计将持续3天，以天为单位将整个应急过程划分为3个阶段，每个阶段的情景描述如下：

第1阶段——天气情况：晴，东北风4～5级。火情预测：在阵风的影响下火势很大，过火面积也在不断扩大，并向公路护坡方向蔓延。

第2阶段——天气情况：晴，西南风2～3级。火情预测：在西南风的影响下，火势进一步加剧，由于风向的变化，火情开始远离护坡，向村庄方向蔓延。

第3阶段——天气情况：中到大雨，无风。火情预测：该阶段火势保持平稳，由于在本地区将出现一次较强降水，对整个火势的控制具有积极作用。

为从备选方案集合中确定1个最为理想的应急方案，应急部门组织20位专家对各个阶段下的备选方案实施效果进行评价。由于各个专家的评价标准不同，首先需要将评价值进行标准化处理[1]，标准化后的偏好信息如表1所示。

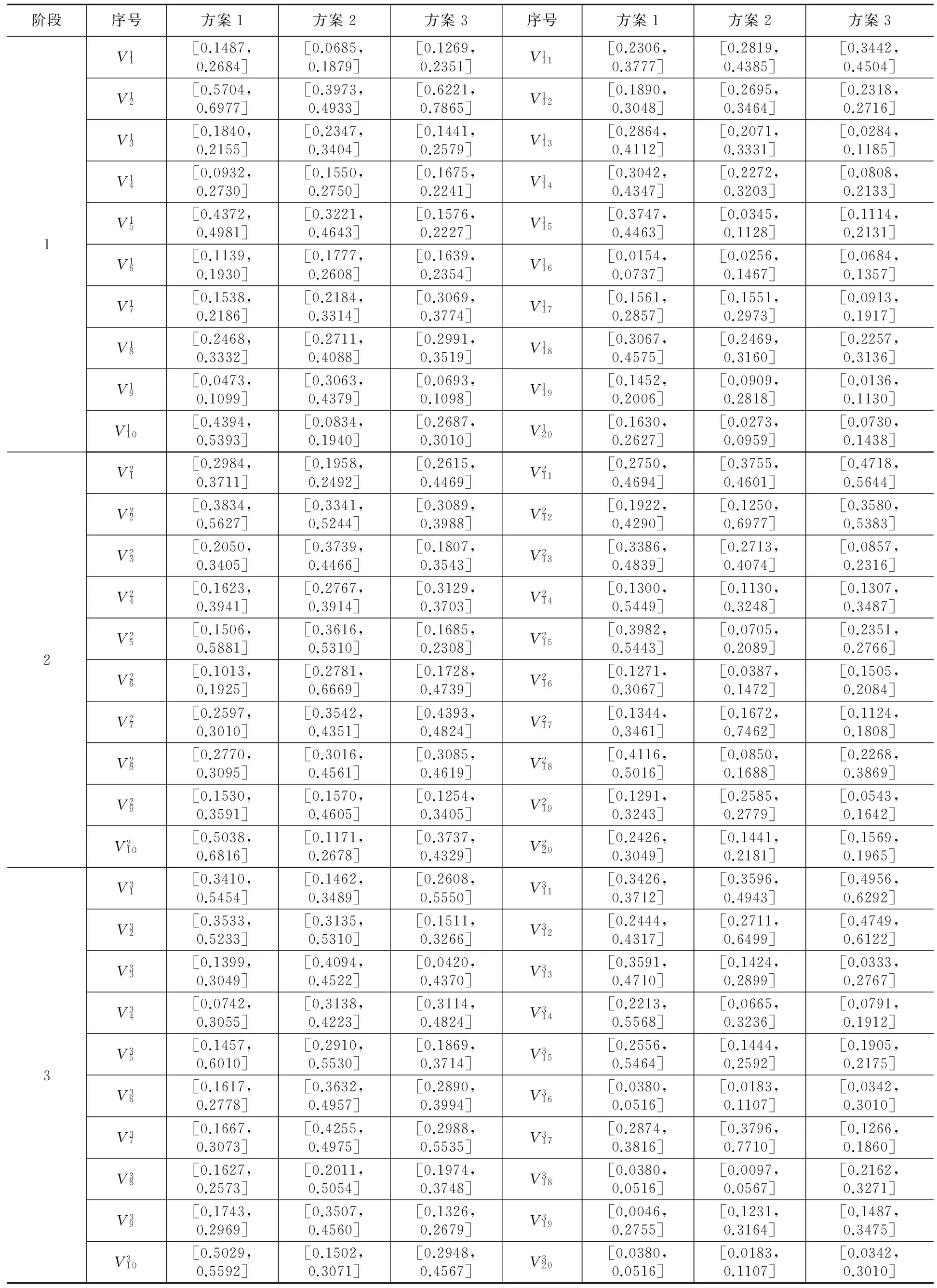
表1 各阶段标准化后的偏好信息

对各个阶段的专家偏好矢量进行聚类(聚类阈值分别取γ1=0.7、γ2=0.78、γ3=0.78)[15]，聚类结果如表2所示。

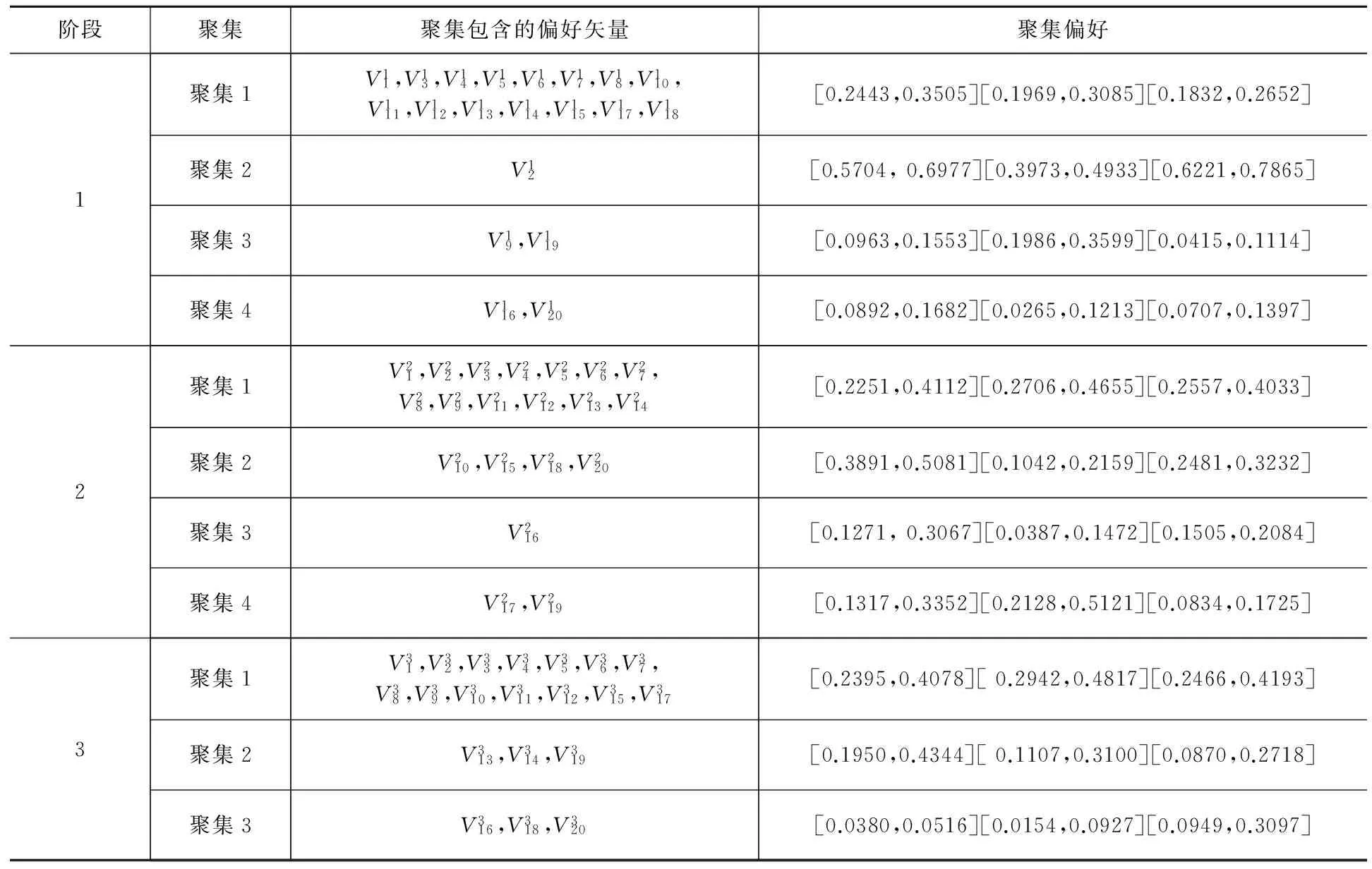
表2 各个阶段的聚类结果

利用式(7)确定各阶段聚集权重：W1=(0.43,0.11,0.20,0.26)T；W2=(0.18,0.23,0.35,0.24)T;W3=(0.22,0.31,0.47)T。

结合各阶段的聚集权重，利用式(5)得到各个阶段的群体偏好：

G1=([0.2102,0.3023][0.1750,0.2904][0.1739,0.2592])

G2=([0.2061,0.3787][0.1373,0.3079][0.1758,0.2613])

G3=([0.1310,0.2486][0.1063,0.2456][0.1258,0.3221])

利用式(10)求解阶段权重：ω=(0.31,0.33,0.36)T，进而得到整个决策过程的群体偏好：G=([0.1804,0.3082][0.1378,0.2801][0.1572,0.2825])。构建备选方案的偏好可能度矩阵Q=(qlf)3×3，利用式(11)求得各个备选方案的排序向量O=(0.4001,0.2888,0.3171)，故方案1为最优方案。

4 结论

本文针对偏好信息表示为区间模糊数的多阶段大群体应急决策问题，提出一种大群体决策方法。该方法首先给出了区间模糊数间的相似度测度公式，将专家偏好划分成若干个聚集，缩小了专家偏好信息的规模，降低了后续的决策难度。分别以同一集合中所有聚集的阶段内偏好冲突水平最小化和所有阶段的综合偏好冲突水平最小化为目标构建相对熵优化模型对阶段内聚集权重和阶段权重进行求解，利用赋权的方法降低了不同类型的偏好冲突，提高了综合群体偏好的一致性。本文提出的方法为解决多方案多阶段的大群体应急决策问题提供了一种新的思路。在未来的研究中，可以将本方法进一步扩展，使其适用于求解具有多属性特征的大群体应急决策问题。

[1] Kuo M S, Liang G S. A soft computing method of performance evaluation with MCDM based on interval-valued fuzzy numbers[J]. Applied Soft Computing, 2012, 12 (1): 476- 485.

[2] Chai J Y, Liu N K, Xu Z S. A rule-based group decision model for warehouse evaluation under interval-valued Intuitionistic fuzzy environments[J]. Expert Systems with Applications, 2013, 40(6): 1959-1970.

[3] Wei G W, Zhao X F, Lin R, Wang H J. Generalized triangular fuzzy correlated averaging operator and their application to multiple attribute decision making[J]. Applied Mathematical Modelling, 2012, 36：2975-2982.

[4] Xu Z S, Cai X Q. On consensus of group decision making with interval utility values and interval preference orderings[J]. Group Decision Negotiation, 2013, 22: 997-1019.

[5] Xu Z S. Multiple attribute group decision making with different formats of preference information on attributes[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B, 2007, 37: 1500-1511.

[6] 陈晓红,刘益凡.基于区间模糊数群决策矩阵的专家权重确定方法及其算法实现[J].系统工程与电子技术,2010，32(10)：2128-2131.

[7] Xu Z S, Chen J. MAGDM linear programming models with distinct uncertain preference structures[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B, 2008, 38: 1356-1370.

[8] Chen T Y. Comparative analysis of SAW and TOPSIS based on interval-valued fuzzy sets: discussions on score functions and weight constraints[J]. Expert Systems with Applications, 2012, 39: 1848-1861.

[9] 周晓光,张强,胡望斌.基于Vague集的TOPSIS方法及其应用[J].系统工程理论方法与应用,2005,14(6):537-541.

[10] 宋光兴，杨槐.群决策中的决策行为分析[J].学术探索，2000,57(3):48- 49.

[11] Xu X H, Chen X H. A conflict measure model and corresponding conflict coordination mechanism in large group decisions[J]. Journal of Systems Science and Information, 2011, 9: 1-18.

[12] 刘勇,Forrest J,刘思峰,赵焕焕,菅利荣.一种权重未知的多属性多阶段决策方法[J].控制与决策,2013,28(6):940-949.

[13] 卢志平,侯利强,陆成裕.一类考虑阶段赋权的多阶段三端点区间模糊数型群决策方法[J].控制与决策，2013,28(11):1756-1760.

[14] Ye J. Cosine similarity measures for intuitionistic fuzzy set and their applications[J]. Mathematical and Computer Modelling, 2011, 53: 91-97.

[15] 徐选华著.面向特大自然灾害复杂大群体决策模型及应用[M].北京：科学出版社,2012.2.35- 40.

[16] 赵萌,邱菀华,刘北上.基于相对熵的多属性决策排序方法[J].控制与决策，2010,25(7):1099-1104.

[17] 邱菀华著.管理决策熵及其应用[M].北京：中国电力出版社，2011.1:235-240.

[18] Xia M M , Xu Z S. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment[J]. Information Fusion, 2012(1): 31- 47.

[19] 徐泽水.不确定多属性决策方法及应用[M].北京：清华大学出版社,2004.105-112.

A Multi-stage Conflict Style Large Group Decision-making Emergency Method Based on Interval Fuzzy Number

XU Xuan-hua1, CAI Chen-guang2, CHEN Xiao-hong3

(SchoolofBusiness,CentralSouthUniversity,Changsha410083,China)

For the multi-period large group emergency decision-making problem that stage weights are unknown and preference information is interval fuzzy number(IFNs), a new group decision-making method is proposed. Firstly,the similarity formula between INs is given, and each stage preference information is clustered by this formula. Then,the trelative entropy method is used to determine cluster weights and stage weights. The alternatives ranking result is obtained based on the comprehensive group preference, and the best alterative is selected. Finally, an example shows the effectiveness and practicability of this method.

emergency management; group decision making; relative entropy; IFNs; multi-stage

2013-10-22

国家自然科学基金资助项目(71171202)；国家创新研究群体科学基金资助项目(71221061);国家社会科学基金重点项目(12AZD109)

徐选华，男，教授，博导，主要研究方向：决策理论与技术，信息系统与决策支持系统，应急管理与决策；蔡晨光，男，博士研究生，主要研究方向：决策理论与方法，应急管理与决策。

C934

A

1007-3221(2015)04- 0009- 07