需求扰动下竞争型闭环供应链的生产与协调决策分析

韩小花， 吴海燕， 王 蓓

(广东工业大学 管理学院，广东 广州 510520)



需求扰动下竞争型闭环供应链的生产与协调决策分析

韩小花， 吴海燕， 王 蓓

(广东工业大学 管理学院，广东 广州 510520)

研究了一个制造商和两个竞争型零售商组成的闭环供应链系统在面临需求扰动时的生产决策与协调机制设计问题。研究发现：当需求扰动不大时，产量和回收率决策具有鲁棒性，但销售价格始终随着需求的扰动而变动；当面临较大的需求正扰动时集中决策者、制造商和零售商都愿意改变生产决策，当面临较大的需求负扰动时集中决策者和制造商也愿意改变决策，但零售商更希望保持原有决策；收入共享契约可以协调扰动前后的闭环供应链，但当存在较大的需求负扰动时零售商要求分享更多的利润。

闭环供应链；竞争；需求扰动；生产决策；收入共享契约

0 引言

随着经济全球化趋势的不断加剧，供应链运作范围不断扩大，其运作过程也极易受到突发事件的影响。一旦突发事件对某个节点企业产生了干扰，就会通过供应链的层级结构迅速扩散到供应链的所有企业，进而对整个供应链的运作产生严重的影响。例如，日本的地震灾害常常导致了全球电脑配件价格的上涨，从而给整个电子行业供应链的运作带来了冲击。再有，供应商的“速成鸡”事件也给肯德基在中国市场的销售带来了较大的影响，其2013年二季度业绩报告显示，中国市场的销售额下滑了12%。

由于突发事件对供应链运作影响的严重性，如何应对扰动环境下供应链的运作问题已经得到了企业界和学术界的广泛重视。扰动管理(Disruption Management)由Clausen等[1]于2001年首先等提出，主要是为了解决航空公司如何应对扰动事件。Qi等[2]首先将扰动管理引入到供应链管理的领域中，研究了需求扰动下双边垄断供应链的协调机制。Huang等[3]在非线性需求函数的情况下，进一步研究了需求发生扰动时双边垄断供应链的协调机制问题。于辉等[4]研究了批发价契约下双边垄断供应链如何应对扰动事件。Chen和Xiao[5]研究了零售商领头的双边垄断供应链系统中生产成本和需求扰动对数量折扣和批发价契约的影响。另外，一些学者还研究了存在竞争零售商的供应链系统中的扰动问题。Xiao等[6]在多个竞争零售商组成的供应链中研究了促销投资敏感系数的扰动对制造商定价与协调的影响。Xiao等[7]研究了需求扰动下如何通过数量折扣契约来协调一个制造商和两个竞争零售商组成的供应链。曹二保和赖明勇[8]研究了需求和成本同时扰动时多零售商供应链的协调问题。Zhang等[9]在需求扰动下研究了收入共享契约如何协调一个制造商和两个竞争零售商的供应链。吴忠和等[10]在一个制造商和两个竞争零售商组成的供应链中，研究了生产成本、市场需求和价格敏感系数同时扰动时数量折扣契约对供应链的协调作用。Huang等[11,12]研究了需求和生产成本扰动下的双渠道供应链定价与生产数量决策问题。

以上研究大都是基于开环供应链的。然而，在重视节能减排、低碳经济的国际背景下，闭环供应链管理已成为企业界和学术界关注的重要议题。由于闭环供应链不仅涉及正向物流，还包括了逆向物流，组织结构以及面临的环境更加复杂多变，更易产生扰动。因而，闭环供应链的扰动管理研究十分紧迫。最近，一些学者在扰动环境下研究了闭环供应链中的生产与协调决策，取得了初步但显著的研究成果。王玉燕[13]研究了需求和成本扰动下双边垄断闭环供应链的生产策略和协调机制。王旭和王银河[14]在市场规模、再制造成本、回收价格敏感系数同时扰动下研究了双边垄断闭环供应链的最优决策和数量折扣契约协调机制。

目前，基于闭环供应链的扰动管理研究主要关注于双边垄断的市场结构以及如何通过数量折扣契约来协调供应链。然而，在实际运作过程中，制造商常常通过多个竞争的零售商来分销产品。而且，收入共享契约在实际中也有非常广泛且有效的应用。鉴于此，本文主要在需求扰动的情况下，研究一个制造商和两个竞争的零售商组成的闭环供应链系统中的生产决策与收入共享契约设计问题。

1 问题描述与相关说明

本文所研究的闭环供应链系统中，制造商可以同时对原材料和废旧产品进行制造和再制造，制造和再制造的产品的性能完全相同，可在同一市场上销售。零售商主要负责销售新产品和回收废旧产品。制造商是闭环供应链的主导企业，两个零售商是跟随企业。闭环供应链的运作过程分为两个阶段：计划阶段和实施阶段。在计划阶段，制造商根据需求函数和预测的市场规模来确定需求量，进而选择最优生产决策，制造商根据计划阶段的决策进行前期的原材料购买和生产准备；在实施阶段，当实际需求发生后，制造商和零售商根据实际需求来选择新的最优生产决策。

2 需求稳定环境下闭环供应链的决策模型

2.1 集中化决策模型

在集中化决策下，制造商和零售商作为一个整体，以整个闭环供应链的利润最大化为目标来进行决策。因此，决策模型为：

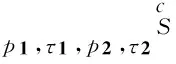
(1)

模型(1)中的第1、2部分代表销售产品1、2所获得的利润，第3、4部分代表回收废旧产品1、2所投入的固定投资。

根据一阶最优性条件计算可得：

命题1 集中化决策下闭环供应链的最优销售价格为:

最优回收率为：

最优生产数量为：

最优利润值为：

2.2 分散化决策模型

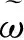
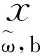
(2)

模型(2)中的第1、2个约束条件表示零售商1、2在各自目标函数最大化下选择最优销售价格和回收率。

最优回收率为：

最优生产数量为：

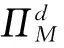
2.3 供应链协调机制设计

由于分散化决策存在双重边际效应，造成了闭环供应链运作的低效率。因此，本节采用收入共享契约来协调闭环供应链。许多学者研究发现，相比于其他契约，收入共享契约能协调更广泛的供应链[16]。针对本文研究的闭环供应链的具体情况，制造商设计的收入共享契约决策模型为：

(3)

模型(3)中目标函数的第1、2部分为制造商批发产品给零售商1,2所获得的利润与向零售商回购废旧产品所付出的成本之差，第3、4部分为制造商与零售商1、2共享的销售收入。模型中的第3、4个约束条件是零售商1、2的参与条件，即确保零售商有动力参与收入共享契约。

命题3 收入共享契约能够协调一个垄断的制造商和两个竞争的零售商组成的闭环供应链，若该契约的参数满足:

3 需求扰动环境下闭环供应链的决策模型

3.1 集中化决策模型

在集中化决策环境下，当需求产生扰动时，决策者可以通过调整计划期的决策来增加利润或减少损失。但是，调整决策会产生偏离成本。因此，决策模型为：

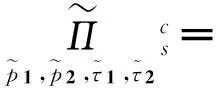
(4)

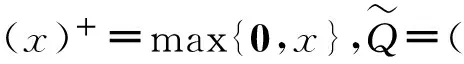
(5)

模型(5)是一个带有约束条件的最优化问题。通过引入Lagrange乘子λ，可知模型(5)存在最优解的KKT(Karush-Kuhn-Tucker)条件为：

当λ=0时，根据KKT条件可以求出δ≥(1-β)μ1时模型(5)的最优解；当λ>0时，根据KKT条件可以求出0<δ<(1-β)μ1时模型(5)的最优解。同理，当δ<0时，模型(4)也可简化为一个带有约束条件的最优化问题，同样可求出当δ≤-(1-β)μ2以及，-(1-β)μ2<δ<0时模型的最优解。将这些最优解(值)整理就得到了命题4。证毕。

通过对模型(4)的最优解(值)的比较计算，我们可以得出以下结论。

结论1 当需求在-(1-β)μ2<δ<(1-β)μ1范围内扰动时，集中化决策下的产量和回收率与计划期决策一样，具有鲁棒性；而销售价格不具有鲁棒性，随着需求的扰动而变化。

具体来说，当需求在-(1-β)μ2<δ<(1-β)μ1范围内扰动时，稳定情况下的产量和回收率保持不变；当扰动δ≥(1-β)μ1时，产量和回收率随着正扰动量的增加而增加；当δ≤-(1-β)μ2时，产量和回收率随着负扰动量的增加而降低。当δ>0时，销售价格随着正扰动量的增加而提高，当δ<0时，销售价格随着负扰动量的增加而降低。

结论2 集中化决策下，闭环供应链的利润随着需求正扰动量的增加而增加，负扰动量的增加而减少；当需求扰动δ≥(1-β)μ1或者δ≤-(1-β)μ2时，集中化决策者调整计划期决策可以给闭环供应链带来更多的利润。

3.2 分散化决策模型

在分散化决策下，当需求产生扰动后，制造商和零售商可以通过调整计划期的决策来增加利润或减少损失，但调整决策也会产生一些偏离成本。制造商和零售商将综合考虑调整决策所带来的利润和偏差成本对他们各自利润函数的影响。由于制造商为供应链的主导企业，因此所产生的偏差成本由制造商来承担。决策模型可以表示为：

(6)

模型(6)中目标函数的第1,2部分为制造商所获得的利润，第3,4部分为制造商调整生产策略所带来的偏离成本。根据文献[2]我们也可以得出：

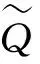
证明 根据引理2，我们将模型(6)分为δ>0和δ<0两种情况讨论。当δ>0时，模型(6)为一个带有约束条件的最优化问题，引入Lagrange乘子λ可得到模型(7)：

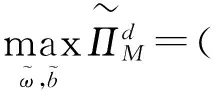
(7)

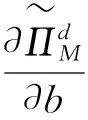
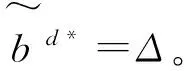
当λ=0时，根据KKT条件可求出δ≥(1-β)μ1时模型(7)的最优解；当λ>0时，根据KKT条件可求出当0<δ<(1-β)μ1时的模型(7)的最优解。同理，当δ<0时，模型(6)也可简化为带有约束条件的最优化问题，进而求出当δ≤-(1-β)μ2以及-(1-β)μ2<δ<0时的模型(6)最优解。将这些最优解(值)进行整理就得到了命题5。证毕。

将需求稳定以及扰动环境下模型(1)、(2)、(4)和(6)的最优解(值)进行比较，可得：

结论3 当需求在-(1-β)μ2<δ<(1-β)μ1范围内扰动时，分散化下的产量和回收率决策与计划期一样，具有鲁棒性；而销售价格不具有鲁棒性，随着需求的扰动而变动。

具体来说，当需求在-(1-β)μ2<δ<(1-β)μ1范围内扰动时，稳定环境下的最优产量和回收率保持不变，当扰动δ≥(1-β)μ1时，产量和回收率随着正扰动量的增加而增加，当δ≤-(1-β)μ2时，产量和回收率随着负扰动量的增加而降低。当δ>0时，销售价格随着正扰动量的增加而提高，当δ<0时，销售价格随着正扰动量的增加而降低。

结论4 在相同的需求扰动下，分散化决策下的销售价格高于集中化的销售价格，产量和回收率低于集中化的产量和回收率。

结论5 在相同的需求扰动下，分散化决策下的闭环供应链总利润小于集中化的总利润。

结论4和5说明，需求扰动下分散化决策存在双重边际效应，决策效率低于集中化决策。

结论6 分散化决策下，制造商和零售商的利润随着需求正扰动量的增加而增加，负扰动量的增加而减少；当δ≥(1-β)μ1时，制造商和零售商可以通过调整计划期决策来获得更多的利润；当δ≤-(1-β)μ2时，制造商可以通过调整决策来获得更多的利润，但决策调整后零售商获得了更少的利润。

也就是说，当需求扰动δ≥(1-β)μ1时，制造商和零售商都愿意考虑需求扰动的影响，调整计划期的决策；当δ≤-(1-β)μ2,制造商也愿意根据扰动的影响来调整决策，但零售商更愿意保持原有决策。这就带来了零售商隐藏需求扰动信息的危险。由于零售商离市场比较近，对需求的扰动信息更具敏感性。当扰动是促使需求增加的，零售商愿意与制造商分享扰动信息，但是当扰动是导致需求减少的，零售商可能会隐藏信息，这样就给整个闭环供应链带来损失。因此，为了避免零售商隐藏需求扰动信息，制造商需要设计更加稳定的协调契约。

3.3 协调机制设计

以上分析发现，当需求扰动时集中化和分散化决策下闭环供应链的销售价格都发生了改变。扰动下与稳定环境下的销售价格不一致，因此稳定环境下的收入共享契约不能协调扰动下的闭环供应链。本节在需求扰动下设计收入共享契约，并通过比较稳定和扰动环境下契约的参数来探讨收入共享契约的抗扰动性。扰动环境下制造商设计的收入共享契约模型为：

(8)

模型(8)中目标函数的第1、2部分为制造商批发产品给零售商所获得的利润与向零售商回购废旧产品的成本之差，第3,4部分为制造商分享零售商的销售收入，第5,6部分是改变决策所产生的偏离成本。模型中第3和4个约束条件是零售商的参与条件，该条件可以避免零售商隐藏需求扰动信息，从而使收入共享契约更加稳定。

当-(1-β)μ2<δ<(1-β)μ1，

当δ≤-(1-β)μ2，

命题3和6表明，收入共享契约可以协调稳定和扰动环境下的闭环供应链，但是它们的分成系数的取值不同。根据对分成系数的比较，我们得出：

结论7 当δ≥(1-β)μ1或-(1-β)μ2<δ<(1-β)μ1时，扰动与稳定环境下的收入分成系数相同；当δ≤-(1-β)μ2时，扰动下的收入分成系数增加，零售商要求获得更多的利润。

4 数值实验

为了更加清晰地反映需求扰动下闭环供应链的相关决策情况，本节对以上模型结果进行数值分析。令 h=300,φ=200,β=0.2,cm=20,Δ=5,μ1=10,μ2=10,δ∈[-20,20]，我们可以得到图1～4。

图1 销售价格变化趋势

图2 回收率变化趋势

图1表明，销售价格不具有鲁棒性，随着需求的扰动而变动。当需求产生正扰动时，销售价格随着扰动量的增加而增加，当需求产生负扰动时，销售价格随着扰动量的增加而降低。无论稳定还是扰动情况下集中化的销售价格低于分散化的销售价格。由图2和3可知，回收率和产量的决策具有鲁棒性。当-8<δ<8时，回收率和产量的决策不变，当δ≥8时，随着正扰动量的增加而提高，当δ≤-8时，随着负扰动量的增加而降低。无论稳定还是扰动情况下集中化的回收率和产量都高于分散化的决策。从图4可看出，需求扰动下分散化决策的闭环供应链的总利润小于集中化决策的总利润。这些数值结果与结论1,3,4和5一致。

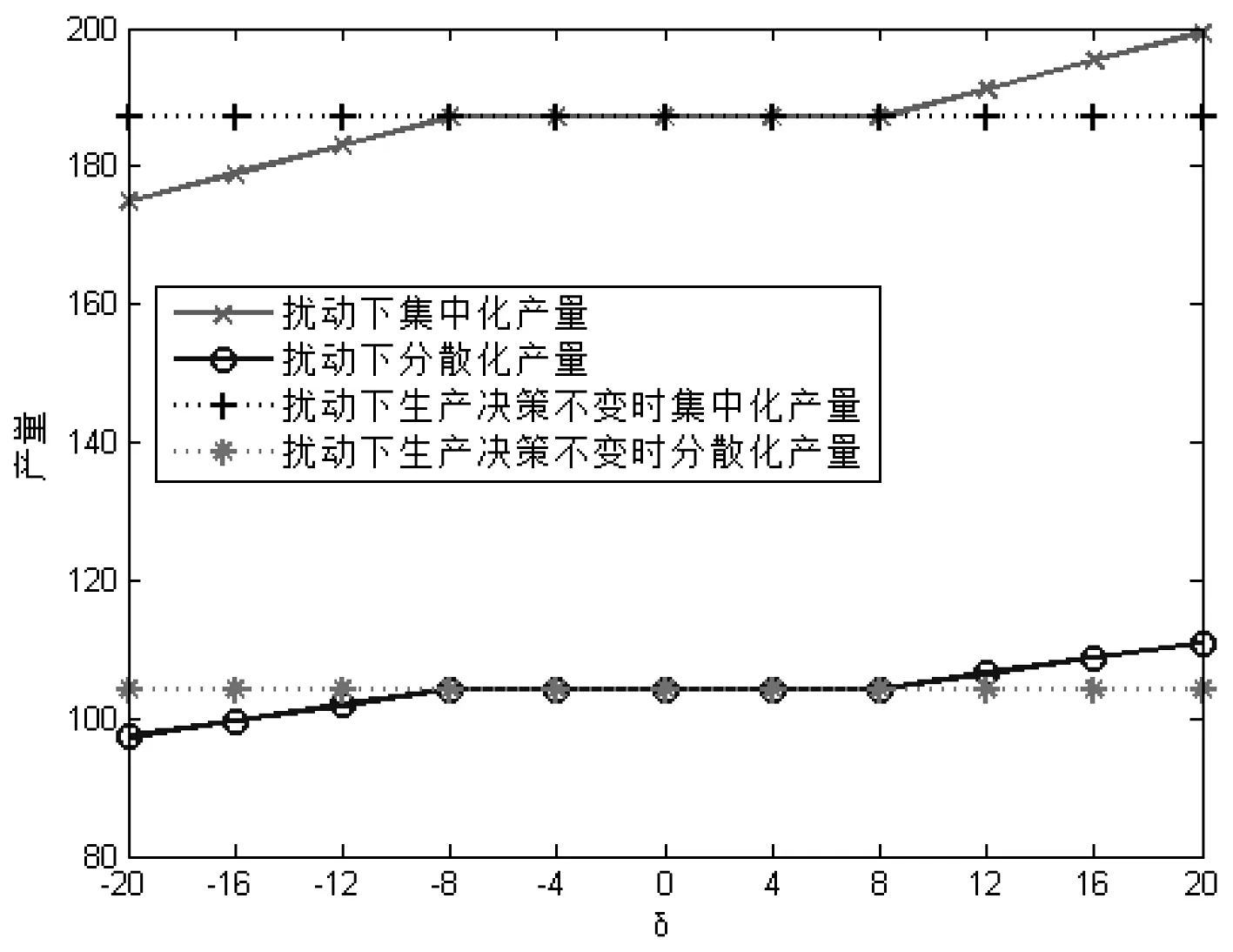
图3 生产产量变化趋势

图4 闭环供应链总利润变化趋势

在δ=20,15,10,5,0,-5,-10,-15,-20情况下，继续分析不同策略对决策者利润的影响以及收入共享契约的协调效果，见表1。

表1 需求扰动下不同决策策略对利润的影响

注：原策略表示生产决策不变的策略，新策略表示考虑扰动的策略，协调策略表示收入共享契约策略。

由表1的第2列可知，当δ≥8或-8<δ<8时收入共享契约的分成系数与稳定环境下的一致，当δ≤-8时分成系数随着需求负扰动量的增加而增加，零售商要求获得更多的利润。由表2的第3，4，6，7，10和11列可知，集中化决策者、制造商和零售商的利润随着需求正扰动量的增加而增加，负扰动量的增加而减少；当需求δ≥8时，集中化决策者、制造商和零售商考虑扰动的利润大于生产决策不变的利润；当需δ≤-8求时，集中化决策者和制造商考虑扰动策略的利润大于决策不变时的利润，但零售商考虑扰动的利润小于决策不变的利润。与结论2和6一致。表2 中的第5，8，9和11列表明，通过收入共享契约可以协调稳定(δ=0)和扰动环境下的闭环供应链，分散化下总利润达到集中化决策下的水平。

5 结束语

开环供应链系统的扰动管理已经有了一些研究，但是针对闭环供应链的扰动研究还不多见，而且大都集中在双边垄断的市场结构中。本文以由一个制造商和两个竞争的零售商组成的闭环供应链系统为研究对象，在集中化和分散化决策情况下，探讨了需求扰动对最优生产决策的影响，并设计收入共享契约协调了扰动前后的闭环供应链。研究表明：需求扰动给闭环供应链带来了较大的影响，闭环供应链的利润随着需求的扰动而变化；当需求扰动不是很大时，集中化决策者、制造商和零售商的产量和回收率决策具有鲁棒性，但销售价格始终随着需求的扰动而变化；当需求的正扰动较大时，集中化决策者、制造商和零售商都愿意考虑扰动来调整生产决策；当需求的负扰动较大时，集中化决策者和制造商愿意考虑扰动来调整决策，但零售商更愿意保持原来决策；收入共享契约可以协调稳定和扰动环境下的闭环供应链，但存在较大需求负扰动时零售商要求分享更多的利润。

本文也存在一些可以扩展的方面。例如，我们只考虑了零售商竞争的单边竞争型闭环供应链，没有涉及由多个制造商和多个零售商组成双边竞争型闭环供应链。然而，在实践中双边竞争型闭环供应链更具普遍性，更具研究价值。再有，我们主要关注需求扰动这一单一因素对闭环供应链生产与协调决策的影响，没有考虑生产成本、回收难易程度等其他多个因素的综合影响，但有时突发事件对供应链系统的干扰是多方面的。因此, 我们未来的研究也将进一步考虑以上决策问题，力图弥补现有研究中的不足。

[1] Clausen J, Hansen J, Larsen J, Larsen A. Disruption management[J]. OR/MS Today, 2001, 28(5): 40- 43.

[2] Qi X T, Bard J, Yu G. Supply chain coordination with demand disruptions[J]. Omega, 2004, 32: 301-312.

[3] Huang C C, Yu G, Wang S, Wang X J. Disruption management for supply chain coordination with exponential demand function[J]. Acta Mathematica Scientia, 2006, 26B (4): 655- 669.

[4] 于辉,陈剑,于刚.批发价契约下的供应链应对突发事件[J].系统工程理论与实践,2006,26(8):33- 41.

[5] Chen K B, Xiao T J. Demand disruption and coordination of the supply chain with a dominant retailer[J]. European Journal of Operational Research, 2009, 197(1): 225-234.

[6] Xiao T J, Yu G, Sheng Z H, Xia Y S. Coordination of a supply chain with one-manufacturer and two retailers under demand promotion and disruption management decisions[J]. Annals of Operations Research, 2005, 135: 87-109.

[7] Xiao T J, Qi X T, Yu G. Coordination of supply chain after demand disruptions when retailers compete[J]. International Journal of Production Economics, 2007, 109: 162-179.

[8] 曹二保,赖明勇.需求和成本同时扰动时多零售商供应链协调[J].系统工程理论实践,2010,30(10):1753-1761.

[9] Zhang W G, Fu J H, Li H Y, Xu W J. Coordination of supply chain with a revenue-sharing contract under demand disruptions when retailers compete[J]. International Journal of Production Economics, 2012, 138: 68-75.

[10] 吴忠和,陈宏,赵千,吴晓志.需求和零售商购买成本同时扰动的供应链应急协调[J].中国管理科学,2012,20(6):110-117.

[11] Huang S, Yang C, Zhang X. Pricing and production decisions in dual-channel supply chains with demand disruptions[J]. Computers & Industrial Engineering, 2012, 62: 70- 83.

[12] Huang S, Yang C, Liu H. Pricing and production decisions in a dual-channel supply chain when production costs are disrupted[J]. Economic Modelling, 2013, 30: 521-538.

[13] 王玉燕,需求与成本双扰动时闭环供应链的生产策略和协调策略[J].系统工程理论实践,2013,33(5):1149-1157.

[14] 王旭,王银河.需求和回收扰动的闭环供应链定价和协调[J].计算机集成制造系统,2013,19(3):624- 630.

[15] Lee E, Staelin R. Vertical strategic interaction: implications for channel pricing strategy[J]. Marketing Science, 1997, 16(3): 185-207.

[16] Cachon G P. Supply chain coordination with contracts[M]. Handbooks in Operations Research and Management Science: Supply Chain Management. North Holland, the Netherlands: Elsevier, 2003.

Production and Coordination Decisions in Competing Closed-loopSupply Chains with Demand Disruptions

HAN Xiao-hua, WU Hai-yan, WANG Bei

(School of Management, Guangdong University of Technology, Guangzhou 510520, China)

This paper studies the production and coordination decisions in one-manufacturer-two-competing-retailers closed-loop supply chains when facing demand disruptions. The results indicate that the optimal production quantity and return rate have some robustness, while the optimal selling price always changes with demand disruptions. We also find that the centralized decision-maker, manufacturer and retailer prefer to adjust their decisions when facing considerably positive disruptions; the centralized decision-maker and manufacturer also prefer to adjust their decisions, but the retailer tends to maintain original decisions when facing considerably negative disruptions. The coordination of closed-loop supply chain with/without disruptions can be achieved by revenue-sharing contracts, while more profits are required by retailers under markedly negative disruptions.

closed-loop supply chain; competition; demand disruptions; production decisions; revenue-sharing contract

2013-10-29

国家自然科学基金资助项目(71101032)；高等学校博士学科点专项科研基金资助项目(20104420120008)

韩小花(1978-)，女，山西大同人，博士、副教授,研究方向：行为运作及供应链管理等；吴海燕(1989-)，女，河北赵县人，硕士研究生，研究方向：供应链管理等；王蓓(1974-)，女，博士、讲师。研究方向：供应链管理等。

F224;F406.7

A

1007-3221(2015)03- 0068-11