自然灾害风险下区域应急储备设施选址可靠性研究
2015-07-07付德强陈煜舟万晓榆
付德强, 陈煜舟, 万晓榆
(1.电子商务与现代物流重庆高校市级重点实验室,重庆 400065;2.重庆邮电大学 经济管理学院,重庆 400065)
自然灾害风险下区域应急储备设施选址可靠性研究
付德强1,2, 陈煜舟1, 万晓榆1
(1.电子商务与现代物流重庆高校市级重点实验室,重庆 400065;2.重庆邮电大学 经济管理学院,重庆 400065)
自然灾害发生时,为了保证区域应急储备系统的服务不被中断,考虑设施被破坏数目的发生概率并提供备份库存,以加强应急储备系统的可靠性。模型采用非支配排序遗传算法(NSGA-II)进行求解,产生一组选址决策方案。以四川省八大城市的人口及运输距离为输入数据的仿真结果表明,与一般模型比较,本文考虑可靠性的选址模型能更好抵御自然灾害造成的中断影响,并且能获得更优的应急响应满意度、多重覆盖或总成本的单目标值。因此,在地震等灾害的破坏风险下,该模型可成为应急储备设施可靠选址的有效工具。
物流设施选址;可靠性研究;NSGA-II;区域应急储备
0 引言
保证系统运作的可靠性一直是物流和供应链领域关注的焦点。近年来,由于各类灾害的频繁发生,国际上管理科学、运筹学界引发了设计具有抵御中断风险的物流或供应链系统的研究热潮[1]。从广义上讲,系统可靠性指的是其中各个组成元素在任何时刻都能有效运转的性质。本文将具有可靠性的物流设施系统规定为:因为外部干扰(自然灾害)导致部分设施服务中断,却仍能及时有效地满足物流需求,并且拥有经济的运作费用和运输费用的物流系统。
Snyder et al.[2]最先对如何构建具有可靠性的选址模型进行了探讨,他们发现如果将灾害发生的概率事先考虑入的选址模型中,可以大大减少不考虑灾害而造成的损失;为此他们设计的P-中值模型不仅能抵御中断风险,而且拥有最小化的成本。但是P-中值模型假设灾害发生时每个设施都有相同的失效概率,这显然不符合实际。 Aboolian et al.[3], Shen et al.[4]和Cui et al.[5]放松这一假设,分别设计了失效概率与设施相关的模型;但采取这种方法往往会导致计算期望运输成本的算式高度的不线性,使得设计有效算法以及计算大样本的困难加大。另一类方法是采用情景遍历的方法[6],考虑所有可能的中断事件;但是其缺陷也是很明显的:当设施的数目不断增大时,模型的求解难度也将更大。此外,以上的各类模型都假定当服务设施被中断时,其所支持的需求点将自动转向下一个最近的设施获取服务;然而在现实中,每个服务设施的库存是固定,没有预先的安排,该设施将很难为新的需求进行服务。
针对现有的研究及不足,本文考虑遍历不同设施失效数目的情景,并按经验分配概率,以降低情景的总个数,建立线性的算式;并在事前就为可能中断的需求提供备份库存。现阶段我国有关应急储备的研究,如李静等[7],郭子雪等[8]和陆相林等[9],未有考虑可靠性的问题,本文拟在付德强等[10]的研究基础上建立具有可靠性的多目标应急储备选址模型:设立应急响应时间满意度、备份覆盖以及成本的三个优化目标,采用NSGA-II算法对多目标模型进行求解;由于该算法高效、易应用的特点[11],所设计的算例可在多项式时间内求解完成。
1 模型的建立
1.1 问题描述及参数定义
本文假设在一个区域内需求点的集合为I,用i标识;应急物资储备库的候选地址集合为J,用j标识;wi代表需求点i的应急需求权重,可根据人口权重进行估计;用dij代表运输距离,c代表单位运输费用;fj代表储备库j的单位储备库建设费用,sj为单位库存维持成本。

设tij为储备库j到需求点i所需的时间,可用dij近似代替;设f(x)代表每个需求点i在应急情景下,应急需求得到响应的时间满意度函数。本文参考马云峰等[12]的研究,采用凹凸时间满意度函数,其具体的公式可参考相应的文献。
设决策变量yijhr在情景hr下i被设施j服务时取1,否则为零;xj在候选设施j处建设储备库时取1,否则取零;uihr在情景hr下需求点i在被二次覆盖时取1,否则为零。
1.2 假设条件
模型的假设条件如下:
(1)本文假设应急储备库储存和运输的应急物资为同一种类型。
(2)区域内各个储备库的运作是独立的,灾害发生时破坏一个设施不会影响其他设施的运作。
(3)如果风险发生时某个应急物资储备库被破坏,则该设施将再无法提供任何服务,需求点需转向其他节点以获得应急物资。
1.3 模型的建立

(1)
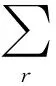
(2)

(3)
(4)

(5)
Yijhr≤xj(1-shrj) ∀i∈I,∀j∈J,∀hr∈Hr,∀r∈R
(6)
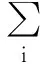
(7)
Yijhr,xj,uihr∈{0,1} ∀i∈I,∀j∈J,∀hr∈Hr,∀r∈R
(8)
式子(1)代表在不同数量设施中断的概率下,最大化需求点的应急响应时间满意度;式(2)代表最大化对需求点的备份覆盖期望值;式(3)代表最小化应急物资储备库的各项成本,其中包括建设设施的固定成本,维持库存Qj的库存费用,以及实施应急物资需求配送的期望运输成本;式(4)代表实际建设储备库数目小于候选物资储备库总数目的50%,以节约成本提高效率;式(5)代表对需求点超额覆盖的约束,使得当ujhr=1时,需求点i至少被储备库覆盖两次,当uihr=0时,需求点被储备库至少覆盖一次;这一约束保证了当设施被中断后,其所覆盖的需求点可由其他正常运转的设施提供服务;式(6)代表只有在j建立了物资储备库且没有被损毁丧失功能时才能给i提供服务;式(7)确定设施j的总库存,总库存量不仅包括正常情况下对需求点提供的物资,也包含预防其他设施中断的备份库存;式(8)限定决策变量都为0-1整数变量。
2 算法设计
NSGA-II,又称非支配排序遗传算法,为现今学界公认求解多目标规划问题十分有效的优化算法,它由印度人KalyanmoyDebetal.[14]于2002年提出。NSGA-II算法的特点是采取了使用精英策略的非支配排序算法(non-dominatedsorting),并设计拥挤距离(crowdingdistance)来求取优良并多样的多目标规划非劣解集。在一般NSGA-II流程基础上,本文为以上模型设计的算法流程如下:
(1)遗传编码,设计染色体
由于本文所建规划的决策变量都为0-1整数变量,故可直接将染色体上每段取值0或1,以代表是否建立设施或提供服务,则种群中每个个体编码设为:Individual=(x1,…,x|I|,y11h1,…,y|I||J||HmR|,u1h1,…,u|I||HmR|)。
(2)初始化种群,满足约束条件
根据染色体编码规则产生数量为pop的初始种群,并使每条染色体上的编码满足约束规则,即:总共建设的设施数小于候选设施数目的一半,部分需求点的服务覆盖大于两次,以及在设施没有建设或被破坏的情形下将无法提供需求。以上都可通过编码过程中限定基因的取值来实现。
(3)计算适应度,进行首次快速非支配排序及计算拥挤距离
NSGA-II中采用快速非支配排序算法来解决在多个目标值间进行权衡优化的问题。在每次算法中,每个种群的每个个体都会被排序,并分在不同的非支配前端集合(non-dominatedfronts)中:在同一个非支配前段集合中,每个个体并不绝对占优因而组成一个front值相同的集合;而在不同的集合间,front值较低的集合一定比front值较高的集合在所有目标函数值上都更优。通过以上的排序分类,每个集合通过front值反映了个体的适应度,以更加适合多目标规划的特性。
在进行快速非支配排列的同时,NSGA-II同时也根据每个个体的每个目标函数值来计算其拥挤距离:通过计算相近的解间的相对目标函数差值,来求得拥挤度值,以此来判断一个种群中某个特定解附近的解集密度;通常一个具有较小拥挤度值的解会被更多的解包围,因而显示较高的多样性特征。
在进行了以上非支配排序和拥挤度操作后,NSGA-II结合front值和拥挤度值的大小对种群中个体进行适应排序:首先拥有较低front值的个体排在前面,随后拥有相同front值的个体按照拥挤度值进行逆序排列。
(4)选择、重组、变异产生子代
从父辈中抽取一定数目的个体进行重组,重组概率设为γ,由于本文中基因编码采用0-1编码,选择两点交叉的重组方法。子代种群产生后,还需要更进一步的对子代进行变异操作,变异概率为μ,采用按位变异的方法实现。
(5)重新对子代进行度量,选择最优产生新的种群
对新的种群重新进行非支配排序以及计算拥挤度,对拥有较高排位的个体进行保留而去除较低排位的个体,以此产生新一代大小为pop的种群。
(6)种群优化结束,取得非劣解集
重复以上的生成新种群—计算适应度—重组变异的过程,直到迭代到达一定标准停止(本文选择迭代至100代为停止条件),最终得到最优的非劣解集。
3 算例设计以及结果分析3.1 算例设计
设I=(1,2,3,4,5,6,7,8),分别顺序代表四川省的八大城市:成都,达州,绵阳,宜宾,泸州,内江,遂宁,乐山;设J=(1,2,3,4,5,6,7,8),代表由上述八大城市组成的设施候选集合;设单位运输成本c=2万元/一百公里·万个物资,固定建设费用fj=350万元,单位库存维持成本sj=2万元/万个(数据来源:根据民政部《救灾物资储备库建设标准》中相关数据平均推算);最大设施失效数目R=2;表1显示了城市间距离dij以及人口权重wi的取值。本文采用NSGA-II对模型进行求解时,设pop=300,迭代次数n=100,重组概率γ=0.9,变异概率μ=0.1。
3.2 帕累托选址方案
根据以上设计的算例,利用matlab软件对模型进行仿真,并采用NSGA-II算法求解,运行环境为:CPU3.30GHz,内存4G。最终得到的解集在各空间中的分布如图1所示,可看出这是一组满足多目标决策问题部分最优条件的Pareto解集。使用NSGA-II算法对300个个体进行100次的迭代后,解集来到了最终的Pareto前端。在由80个点形成的弧形区域中,没有一个方案可以在三个目标函数值上全部占优。比如在(成本,时间满意度)象限中,拥有较低成本的方案在时间满意度上的值也较低,这与要达到更及时的应急响应必须进行更大投资的现实相符合;而在其他象限中,在两个目标值上占优的方案却在第三个目标上处于劣势,从而证明了由算例得出的多目标解集的可效性。

表1 八大候选城市间的运输距离以及人口权重值表 距离单位:公里
由求得的帕累托解集,决策者可根据自身的主观判断来选取方案进行选址:如果对成本目标值较为敏感,可在弧区下部寻找方案;如关心备份覆盖的范围更大,可从弧区上部选取;而如果关心应急响应的满意度,需从弧区前部挑选;决策者也可以设计主观评价工具,为三个目标值赋予权值,将多目标值整合为单目标值并选取最满意的方案。

图1 最终的帕累托解集在各个空间的分布图
3.3 可靠性模型对比一般模型
以下将本文考虑可靠性的模型与不考虑灾害风险的一般模型在各单目标规划中进行比较。所谓一般模型,即不考虑各种中断情景及其发生的概率,且没有公式(6)中(1-ahrj)的约束;如果设施被中断,其服务的各个需求点将转向提供备份覆盖的设施,否则应急需求将无法得到满足。具体比较结果见表2,3,4。
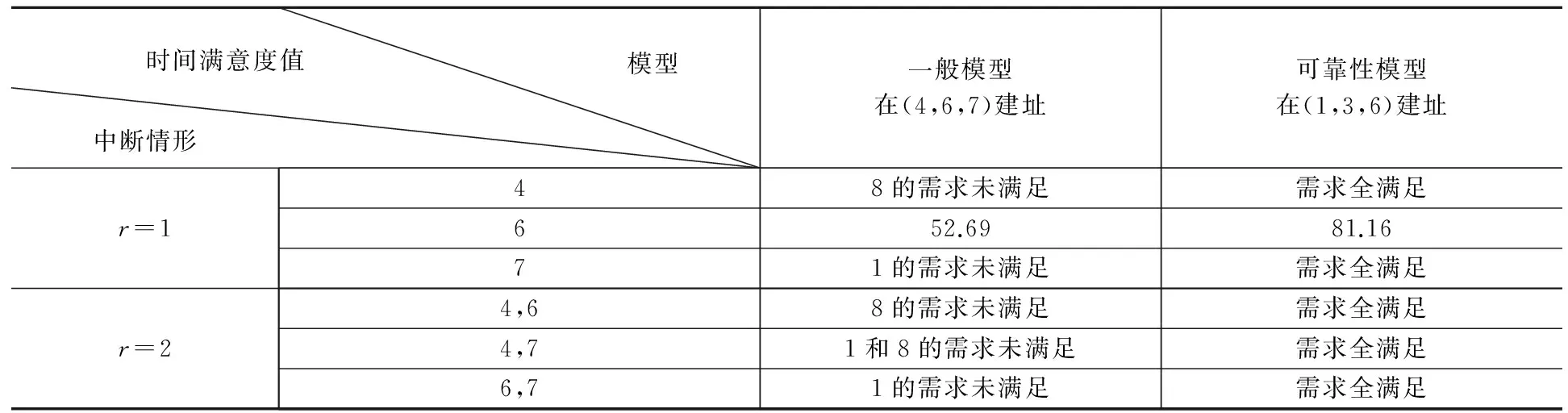
表2 灾害发生时考虑可靠性的模型与一般模型时间满意度值比较

表3 灾害发生时考虑可靠性的模型与一般模型多重覆盖值比较

表4 灾害发生时考虑可靠性的模型与一般模型成本值比较
从以上各表的对比可以看出,灾害发生时考虑可靠性的模型比一般模型能获得更优的单目标值,并能在部分设施服务被中断的情形下,满足全部需求点的应急需求,从而保证了应急储备系统的可靠性。如表2中,当应急储备系统中设施4遭到中断时,一般模型得到的方案(4,6,7)无法满足设施8的需求,而考虑可靠性的模型可以保证所有的应急需求得到满足;当设施6遭到中断时,两个模型都可以满足全部需求,但考虑可靠性的模型能比一般模型获得更高的时间满意度值;从表3和表4中也可以看出,本文设计的模型可以得到更加可靠的选址方案,并且在满意度或多重覆盖的单目标上也可以获得较优的值。
4 结论
本文考虑解决自然灾害可能导致应急储备系统服务被中断的问题,建立了一个可以保证可靠性的应急储备库多目标选址模型。模型中引入不同失效数目概率并对各情形进行枚举,较前人的方法更易于求解;采用在事前备份库存的方法,以更符合真实情况。本文根据模型特点设计NSGA-II算法进行求解,并采用真实数据仿真得到帕累托解集,验证了模型的有效性,并为决策者提供了可行的方案。最后,在与一般模型的比较后发现,考虑可靠性的模型能更好的抵御灾害中断造成的影响,在保证应急储备系统正常运转的同时,也能提供更及时、经济、高效的物资调配。
本文未来的研究方向包括:(1)本文假设各个储存设施的运作是独立的,而灾害发生时,破坏是可以传递的,所以设施间应存在关联。(2)本文假设一个储备设施被损毁后就会完全丧失所有的运作性能,而在实际情况下,这种损失并不一定是完全的,设施可能只是丧失了部分的性能。
[1] Snyder L V, Atan Z, Peng P, et al. OR/MS models for supply chain disruptions: a review[J]. Available at SSRN 1689882, 2012.
[2] Snyder L V, Daskin M S. Reliability models for facility location: the expected failure cost case[J]. Transportation Science, 2005, 39(3): 400- 416.
[3] Aboolian R, Cui T, Shen Z J M. An efficient approach for solving reliable facility location models[J]. INFORMS Journal on Computing, 2012, 25(4): 720-729.
[4] Shen Z J M, Zhan R L, Zhang J. The reliable facility location problem: Formulations, heuristics, and approximation algorithms[J]. INFORMS Journal on Computing, 2011, 23(3): 470- 482.
[5] Cui T, Ouyang Y, Shen Z J M. Reliable facility location design under the risk of disruptions[J]. Operations Research, 2010, 58(4-part-1): 998-1011.
[6] Peng P, Snyder L V, Lim A, et al. Reliable logistics networks design with facility disruptions[J]. Transportation Research Part B: Methodological, 2011, 45(8): 1190-1211.
[7] 李静,赵林度.基于时间满意的应急物资储备库双容量限制选址模型[J].东南大学学报:自然科学版,2007,37(2):393-396.
[8] 郭子雪,齐美然,张强.基于区间数的应急物资储备库最小费用选址模型[J].运筹与管理,2010,(1):15-20.
[9] 陆相林,侯云先.基于设施选址理论的中国国家级应急物资储备库配置[J].经济地理,2010,30(7):1091-1095.
[10] 付德强,张伟,等.基于NSGA-II的灾害随机环境下应急储备库多目标选址决策模型研究[J].软科学,2013,27(11):48-52.
[11] 卫田,范文慧.基于NSGAII的物流配送中车辆路径问题研究[J].计算机集成系统制造,2008,14(4):778-784.
[12] 马云峰,张敏,杨珺.物流设施选址问题中时间满意度函数的定义及应用[J].物流技术,2005,(9):26-29.
[13] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. Evolutionary Computation, IEEE Transactions on, 2002, 6(2): 182-197.
The Study on the Reliable Model for the Regional Emergency Storage Facility under the Risk of Natural Disaster
FU De-qiang1,2, CHEN Yu-zhou1, WAN Xiao-yu1
(Key Laboratory of Online-business and Modern Logistic, Chongqing 400065, China; Chongqing University of Posts and Telecommunications, Chongqing 400065, China)
In order to protect services of regional emergency storage from being interdicted by large-scale natural disasters, we consider the probabilities of the number of facilities being interdicted and store back-up storage to enhance the reliability of location decision. The model is solved with Non-dominated Sorting Genetic Algorithm(NSGA)and a Pareto solution is obtained. The results from the instance of eight major cities in Si-Chuan province suggest that, compared to the generic model, our reliable model can deter the interdiction effect brought by natural disasters in a better way; it can also get better emergency response satisfaction value, multiple coverage value and total cost. Thus, under the chance of being interdicted by earthquake, this model should be a reliable tool to locate the emergency storage facilities.
logistic facility location; reliability study; NSGA-II; regional emergency storage
2014- 09-24
国家自然科学基金资助项目(60905066/F030707);重庆市教委自然科学基金资助项目(KJ070509);重庆邮电大学青年科学研究项目(A2012-95);电子商务与现代物流重庆高校市级重点实验室开放基金资助项目(ECML201411)
付德强(1976-),男,博士,研究方向:物流与供应链管理;陈煜舟(1988-),男,硕士,研究方向:应急物流规划。
F251.2
A
1007-3221(2015)03- 0014- 06
