有限理性条件下考虑决策者动态期望的多属性决策方法
2015-07-07姜广田
姜广田
(大连交通大学 经济管理学院,辽宁 大连 116028)
有限理性条件下考虑决策者动态期望的多属性决策方法
姜广田
(大连交通大学 经济管理学院,辽宁 大连 116028)
有限理性条件下针对带有决策者期望的多属性决策问题,提出一种基于累积前景理论的决策分析方法。在本文中,首先考虑了决策者的有限理性的心理行为特征,以决策者在不同时期对各属性的特定期望作为参照点,然后将具有正态分布信息形式的决策矩阵转化为相对于各参照点的益损决策矩阵,在此基础上,考虑决策者对待收益和损失的不同理性态度,依据累积前景理论计算各时期中每个方案的前景值,并计算关于整个时期的综合前景值,然后依据综合前景值的大小对所有方案进行排序。最后,通过一个算例说明了该方法的可行性和有效性。
决策理论;多属性决策;累积前景理论;心理行为
0 引言
多属性决策是指具有多个属性的有限方案排序或选择问题[1],是现代决策理论的一个重要内容,具有广泛的实际背景。在现实中,决策者可能会在不同时期对各属性有特定的期望要求[2],例如,决策者在股票投资的过程中,可能在不同时期对股票的投资额、风险损失、风险盈利等属性有不同的期望要求。因此,如何解决考虑决策者动态期望的多属性决策问题,具有学术研究价值和现实意义。目前,有关此类决策问题的研究已引起一些学者的重视,但具有针对性的决策分析方法还不多见。从已有的相关文献来看,学者们的研究成果可分为两个方面。一方面的研究是假设决策者的行为完全理性,以期望效用理论为基础。该方面研究的成果可以看到,文献[3]提出了基于期望获得线性分段函数的决策方法,该方法从概率分布函数来获得不完全信息,结合可接受度分析方法给出方案排序等级;文献[4]提出了基于效用评估的决策方法,该方法通过划分效用区间对偏好信息进行集结,从而得到方案的排序;文献[5]提出了加权期望效用的决策方法,该方法依据状态的效用偏好缩小可行域而得到最优方案。文献[6]和[7]提出了交互效用的决策方法,该方法通过不断调整期望水平优化方案集,进而选择最优方案。另一方面的研究是考虑决策者的行为有限理性[8,9],即考虑决策者在行为上并不追求效用最大化,而是选择满意度最大的方案[10]。这种将决策者的心理行为特征引入到多属性决策分析中的研究成果主要有,文献[11]针对随机多准则决策问题,提出了一种基于前景理论的决策方法,该方法定义了一种区间灰色数排序方法及前景价值函数计算各方案的前景值,进而得到方案的排序结果;文献[12]针对风险决策问题,提出一种基于语言评价和累积前景理论的多准则决策方法,该方法将语言评价信息转化为区间数并依据参考点计算各方案的前景值,得到方案的排序结果;文献[13]针对属性值为随机变量的随机多属性决策问题,提出一种基于前景随机占优准则的随机多属性决策方法,该方法将决策者的行为因素引入随机多属性决策, 将具有随机变量的决策矩阵转化为关于参考点的收益和损失矩阵,并构建相应的前景随机占优关系矩阵,进而得到了方案的排序结果。
上述提及的方法为解决有限理性条件下带有决策者动态期望的多属性决策问题提供了较好的思路和支撑。但在现实决策中,会遇到决策者的期望和属性值的类型是正态随机变量的形式且数据信息来自于不同时期的情形,即有限理性条件下带有决策者动态期望的属性值为正态随机变量的多属性决策问题,例如,对于机械设备选择问题,主要考虑使用寿命、可靠性、可维修性等属性,而这些属性往往难以量化,其期望值和属性值通常是以正态随机变量的形式表示。因此,有限理性条件下针对带有决策者动态期望的属性值为正态随机变量的多属性决策问题的研究是值得关注的,具有实际意义。为此,本文给出一种基于累积前景理论[14]的决策分析方法,该方法依据决策者在不同时期针对各属性给出的不同期望作为参照点,将决策矩阵转化为关于各时期参照点的益损决策矩阵,进而考虑决策者对待各时期收益和损失的不同心理态度,计算各方案关于整个时期的综合前景值,并依据综合前景值的大小对方案进行排序。
1 问题描述



依据概率统计知识中的3σ原则可知,X的值落在区间[μ-3σ,μ+3σ]内的概率为P{μ-3σ 另外,在多属性决策问题中,属性的类型可以是成本型或效益型,成本型属性的属性值越小越好,效益型属性的属性值越大越好[15]。记Qc和Qb分别表示成本型属性和效益型属性的下标集合,则有QcUQb=QN,QcIQb=Ø。本文要解决的问题是依据决策者的期望向量Q、属性权重向量w和决策矩阵X,如何通过一个决策分析方法得到所有方案的排序结果。 为了解决上述问题,下面阐述本文提出的有限理性条件下考虑决策者动态期望的决策方法。 首先,确定不同时期中各属性的参照点。决策者的预期目标可以作为参照点,且预期目标作为参照点能够准确地表达决策行为有限理性的特征,并可很好地继承前景理论的各种性质[16],故此决策者对各属性的动态期望可视为不同时期的预期目标,这样,决策者在不同时期对各属性的期望值作为该时期中各属性的参照点。 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) 其次,依据简单加权原则,计算各时期中每个方案的综合前景值Utl(Ai),其计算公式为 (24) 最后,计算每个方案的综合前景值U(Ai),其计算公式为 (25) 显然,U(Ai)越大,方案Ai越好。因此,依据U(Ai)值的大小,可对方案进行排序。 综上所述,基于累积前景理论的动态多属性决策方法的计算步骤如下: 步骤4 依据式(24)、(25),计算每个方案的综合前景值U(Ai),并根据U(Ai)值的大小对所有方案进行排序。 考虑一个X风险投资公司的投资项目选择问题。X公司为了拓展业务,拟对一个项目进行分期投资,现有五个投资方案(A1,A2,A3,A4,A5)可以选择,考虑的四个属性是:投资额(C1,单位:万元)、风险损失值(C2,单位:万元)、风险盈利值(C3,单位:万元)、投资回报率(C4),属性的权重向量为w=(0.3,0.25,0.25,0.20)。决策者针对各属性给出三个不同时期(t1,t2,t3)的评价值,如表1~3所示,时期(t1,t2,t3)的权重向量为wt=(1/6,2/6,3/6)。决策者在(t1,t2,t3)时期针对各属性的期望向量分别为Q1=(N(460,1802),N(300,1252),N(110,902),N(9,92)),Q2=(N(380,1452),N(260,802),N(130,652),N(8,62))、Q3=(N(370,1152),N(255,752),N(135,402),N(6,32))。为了解决该决策问题,下面简要说明采用上文给出方法的计算过程。 表1 具有正态随机变量的决策矩阵D(t1) 表2 具有正态随机变量的决策矩阵D(t2) 表3 具有正态随机变量的决策矩阵D(t3) 首先,以各时期中决策者针对各属性的期望向量Q1,Q2,Q3作为参照点向量,依据式(1)~(12),将参照点向量规范化为O1=(N(0.54,0.182),N(0.56,0.192),N(0.27,0.222),N(0.18,0.182))、O2=(N(0.61,0.152),N(0.61,0.122),N(0.32,0.162),N(0.3,0.222))、O3=(N(0.62,0.22),N(0.6,0.122),N(0.33,0.12),N(0.38,0.192))决策矩阵规范化为矩阵 其次,依据式(13)~(22)计算属性值相对于参照点的收益或损失,并建立相对于参照点的益损决策矩阵如下: 然后,依据式(23),计算每个方案针对各属性的前景值,并建立前景决策矩阵如下: 这里α、β和θ的取值采用文献[14]中的实验数据,即α=β=0.88,θ=2.25。在此基础上,根据式(24)和(25)计算得到每个方案的综合前景值为:U(A1)=0.06,U(A2)=0.02,U(A3)=0.08,U(A4)=-0.17,U(A5)=-0.23。最后,根据得到的每个方案综合前景值,可得到方案的排序结果为:A3fA1fA2fA4fA5。 本文针对有限理性条件下带有决策者动态期望的多属性决策问题,给出了一种决策分析方法。该方法考虑了决策者面对收益和损失具有不同风险态度的心理行为特征,将决策者在不同时期中对各属性的特定期望作为参照点,依据累积前景理论,构建相对于各时期参照点的益损决策矩阵和前景决策矩阵,并在此基础上,通过计算整个决策时期中各方案的综合前景值来得到方案的排序结果。该方法计算过程简单,有较强的可操作性和实用性,为解决考虑决策者有限心理行为因素的决策问题提供了一种新的途径,具有实际应用价值。 [1] Hwang C L, Yoon K. Multiple attribute decision making: methods and applications[M]. New York: SpringerVerlag, 1981. 1- 10. [2] Tsetlin I, Winkler R L. On equivalent target-oriented formulations for multiattribute utility[J]. Decision Analysis, 2006, 3(2): 94-99. [3] Lahdelma R, Salminen P. Pseudo-criteria versus linear utility function in stochastic multi-criteria acceptability analysis[J]. European Journal of Operational Research, 2002, 141: 454- 469. [4] Wang Y M, Yang J B, Xu D L. A preference aggregation method through the estimation of utility intervals[J]. Computers & Operations Research, 2005, 32(8): 2027-2049. [5] Jacquet-Lagrèze E, Siskos Y. Assessing a set of additive utility functions for multicriteria decision making: the UTA method[J]. European Journal of Operational Research, 1982, 10: 151-164. [6] Lotfi V, Stewart T J. An aspiration-level interactive model for multiple criteria decision making[J]. Computers & Operation Research, 1992, 19(7): 671- 687. [7] Wang J G, Zionts S. The aspiration level interactive method(AIM)reconsidered: robustness of solutions[J]. European Journal of Operational Research, 2006, 175(2): 948-958. [8] Simon H A. A behavioral model of rational choice[J]. Quarterly Journal of Economics, 1955, 69(1): 99-118. [9] Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-291. [10] 刘作仪,查勇.行为运作管理: 一个正在显现的研究领域[J].管理科学学报,2009,12(4):64-74. [11] 王坚强,周玲.基于前景理论的灰色随机多准则决策方法[J].系统工程理论与实践,2010,30(9):1658-1663. [12] 胡军华,陈晓红,刘咏梅.基于语言评价和前景理论的多准则决策方法[J].控制与决策,2009,24(10):1477-1482. [13] 张晓, 樊治平.一种基于前景随机占优准则的随机多属性决策方法[J].控制与决策,2010,25(12):1875-1879. [14] Tversky A, Kahneman D. Advances in prospect theory: cumulative representation of uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5(4): 297-323. [15] 夏勇其,吴祈宗.一种混合型多属性决策问题的TOPSIS方法[J].系统工程学报,2004,19(6):630- 634. [16] Chip H, Richard P L, Wu G. Goals as reference points[J]. Cognitive Psychology, 1999, 38(1): 79-109. [17] Ishibuchi H, Tanaka H. Multiobjective programming in optimization of the interval objective function[J]. European Journal of Operational Research, 1990, 48(2): 219-225. [18] Bromiley P. A prospect theory model of resource allocation[J]. Decision Analysis, 2009, 6(3): 124-138. [19] Avineri E. The effect of reference point on stochastic network equilibrium[J]. Transportation Science, 2006, 40(4): 409- 420. Method for Multiple Attribute Decision Making Considering DecisionMaker’s Dynamic Aspiration Under Bounded Rationality JIANG Guang-tian (School of Economics and Management, Dalian Jiaotong University, Dalian 116028, China) This paper proposes a method based on cumulative prospect theory to solve the multiple attribute decision making problems with decision maker’s dynamic aspiration. In this paper, the psychological behavioral factors of decision makers are considered firstly, and the dynamic aspiration of the decision maker with respect to each attribute at different periods is chosen as the reference point. Then, the decision matrix with normal random variables is transformed into the decision matrix of gains or losses relative to each reference point. Furthermore, considering the decision maker’s different psychological attitudes toward gains and losses in decision maker’s mind, the prospect value of each alternative at each phase is calculated based on cumulative prospect theory, and the comprehensive prospect value of each alternative throughout the whole period is calculated. Based on the obtained comprehensive prospect values, a ranking of alternatives is determined. Finally, a numerical example is used to illustrate the feasibility and validity of the proposed method. theory of decision making; multiple attribute decision making; cumulative prospect theory; psychol-ogical behavior 2013- 05-21 国家自然科学基金资助项目(71271050,71301015);教育部人文社会科学研究规划基金资助项目(13YJA630060) 姜广田(1978-),男,辽宁大连人,讲师,博士,研究方向:决策理论与方法。 C934 A 1007-3221(2015)03- 0020- 07

2 决策方法




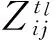

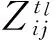



3 算例



4 结束语
