基于ADAMS的大功率采煤机高速区齿轮裂纹故障分析

徐 丹，谢友浩，刘后广，程 刚，刘晓乐

(1.中国矿业大学 机电工程学院，徐州 221116；2.安徽长丰扬子汽车制造有限责任公司，滁州 239064)

0 引言

2013 年，我国原煤产量占能源生产总量的67.5%，煤炭高效、安全开采是我国能源供给的重要保证。大功率采煤机作为现代机械化采煤作业的主要机械设备，其安全稳定运行，直接决定着整个煤矿的安全和产能。然而，因在重载、冲击和变载荷等复杂服役条件下工作，大功率采煤机故障频发。统计资料显示，其摇臂传动系统是故障易出现部位[1]，故障率占大功率采煤机总故障比率34.2%[2]，而其中的高速区齿轮更是故障高发区[3]。可见，研究高速区齿轮故障演化动态特性，为大功率采煤机故障诊断算法设计提供理论参考，进而确保采煤机可靠运行，对煤炭开采至关重要。

本文以MG900/2215-GWD型大功率采煤机高速区齿轮减速器为研究对象，基于ADAMS对其建立齿轮健康及裂纹故障状态下的动力学模型，得到在不同状态下的动态特性。

1 采煤机高速区动力学模型的建立

1.1 建立高速区齿轮传动三维模型

MG900/2215-GWD型采煤机高速区两级直齿圆柱齿轮减速器中所有的齿轮压力角均为20°，齿轮其余参数如表1所示。

在利用UG8.0绘制出各个齿轮或者齿轮轴后，根据齿轮装配原则，进行装配，保证装配中心距，装配出高速区直齿圆柱齿轮减速器。为了防止仿真时出现干扰，此装配没有转配轴承等零件。将三维模型导入ADAMS中，如图1所示，其中齿轮2、齿轮5、齿轮6和齿轮7为惰轮。

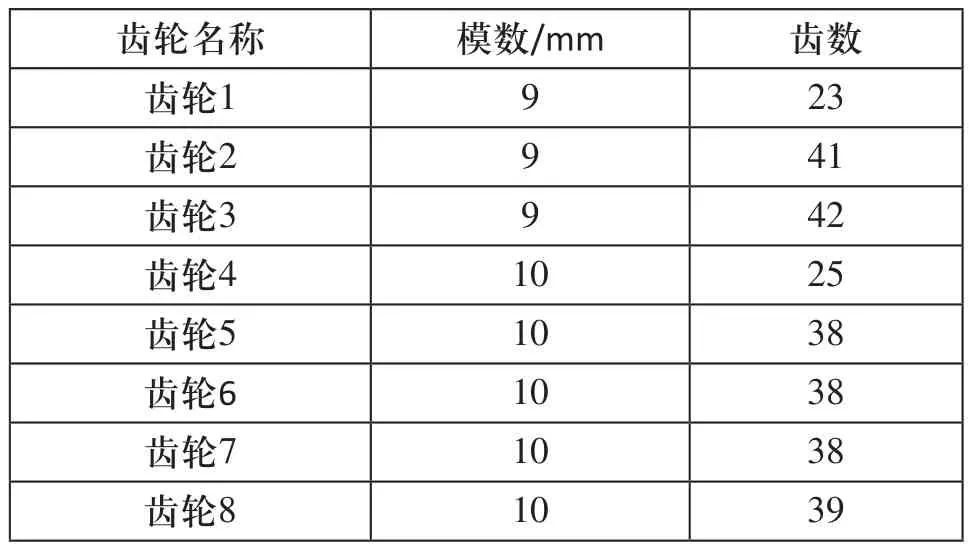
表1 高速区两级直齿圆柱齿轮减速器各齿轮参数

图1 采煤机高速区在ADAMS中动力学模型

根据实际情况，并且结合齿轮运动的传动规律，在本次仿真分析中，特加入以下载荷以及约束[4]：在齿轮3和齿轮4上施加固定副，固定副施加在齿轮4上；以大地为机架，给除了齿轮3的各个齿轮施加旋转副；为了实现齿轮啮合传动的仿真，要给每对接触的齿轮施加碰撞力。为了给系统提供动力，在输入轴处，给该旋转副施加转速驱动，为恒定值。为了模拟该固定轮系的输出负载，要在输出轴上施加一个负载转矩。

1.2 确定contact(接触力)中的参数

齿轮在传动时连续接触，在ADAMS求解中，利用连续算法，需要确定的参数[5,6]如下。

1）计算刚度系数（Stiffness）K

根据赫兹（Hertz）碰撞理论，在解决轮齿碰撞时引起的冲击力时，可视为两个变曲率半径柱体撞击的问题。当考虑截面积为圆形的时候，根据公式（1）计算接触变形：

其中，P代表在撞击时的法向接触力，δ代表接触变形，由此得出：

由公式（2）得出刚度系数计算公式，如式（3）所示：

式中：

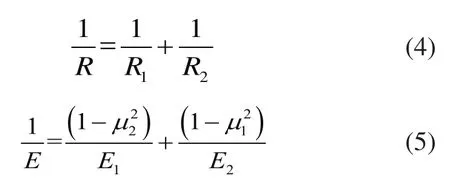
其中R1、R2代表接触时，接触在点物体的当量半径，E代表接触物体材料的弹性模量。µ1、µ2代表接触物体材料的泊松比，E1、E2代表接触物体材料的弹性模量。

2）指数（Force Exponent）e

在仿真过程中，考虑到仿真的速度以及收敛性，取e=1.5。

3）阻尼（Damping）C

在ADAMS中，阻尼系数一般为刚度的百分之一，在经过多次仿真试验对比中，取阻尼系数为。

4）侵入深度（Penetration Depth）

侵入深度应与最大阻尼力对应，通过在ADAMS合理取值，取侵入深度的值为0.01。

5）系统的摩擦

选择coulomb（库仑法）计算齿轮接触时的摩擦力。在进行仿真时，取静态系数 µs=0.08；取动态系数 µd=0.05；取静滑移速度vs=0.1mm/s；取动滑移速度vd=0.1mm/s。

1.3 其他参数的设置

基于本文的齿轮模型系统，在主动轮（齿轮1）上施加很定转速驱动8928deg/sec（1488r/min）。根据本文齿轮传动规律，可知输出轴负载转矩应和主动轮上的转速驱动方向相反，并且为了保证仿真所施加负载不会出现任何突变，在仿真中，要使用STEP函数，使其在0.05s内平缓地施加，具体函数为STEP（time,0,0,0.05,-12684900），其中time为时间自变量。

2 仿真结果及分析

2.1 仿真simulation参数设计

为了防止太大的步长会导致系统参数变化非常激烈而不出现收敛现象，在综合考虑众多影响因素后，设置仿真时间为0.2s，步长取0.0001s，对虚拟样机的分析类型为Dynamics。

2.2 齿轮转速仿真

通过ADAMS仿真，将仿真曲线图，即齿轮1所在轴（输入轴）、齿轮2所在轴、齿轮8所在轴（输出轴）转速随时间t变化曲线导出，由于各个齿轮的轴线与坐标中X轴是平行的，假设逆时针为正向。如图2所示。

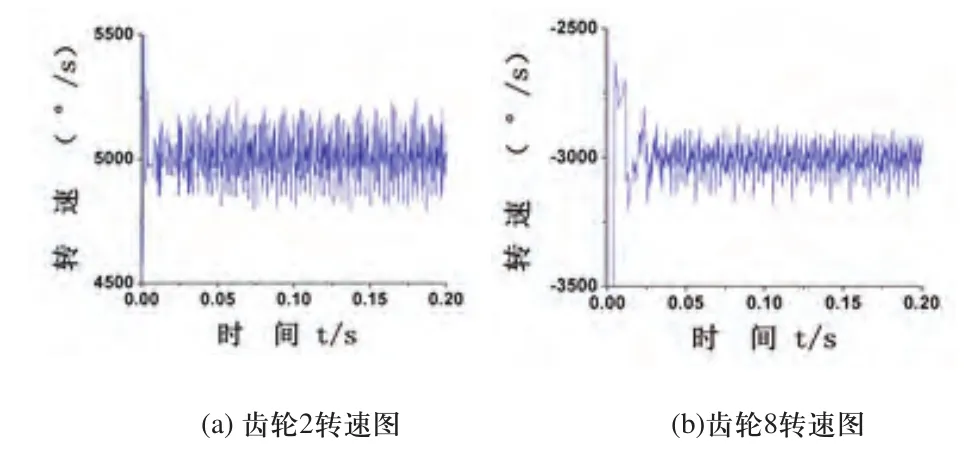
图2 齿轮2、齿轮8转速曲线图

由于齿轮传动过程中存在的冲击以及振动，会在一定范围周期性波动。仿真值按照0至0.2s转速恒定阶段的平均值选取，并计算相对误差。齿轮2转速仿真值为5003.78deg/sec与理论值4878.66deg/sec误差为2.56%，齿轮8转速仿真值为3004.4831deg/sec与理论值3127.38deg/sec误差为3.93%。由于误差λ＜5%，因此各个齿轮转速仿真值和理论计算值在允许误差范围内是一致的，体现出仿真的准确信。

3 摇臂高速区齿轮裂纹故障建模及动态特性分析

3.1 裂纹故障齿轮动力学模型的建立

在大功率采煤摇臂高速区中，齿轮1所在轴为高速区传入轴，其转速最高，发生故障的可能性最大，因此，在健康模型的基础上，对齿轮1的同一位置分别建立1/3裂纹模型和1/2裂纹模型。裂纹模型图如图3所示。

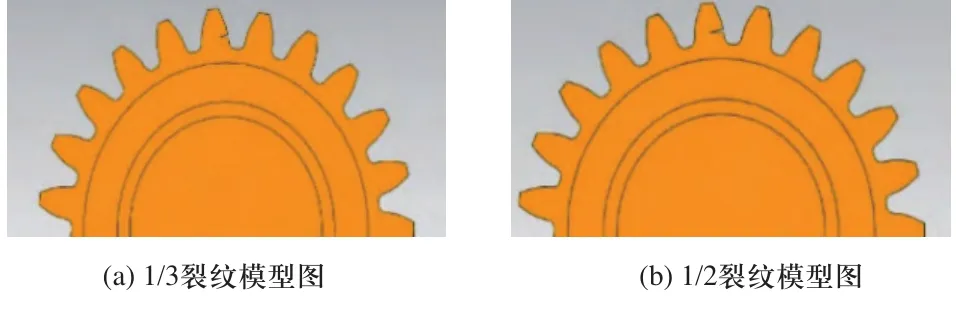
图3 齿轮1的1/3裂纹和1/2裂纹模型图

3.2 动态响应时域对比分析

以齿轮1、齿轮2的齿轮对的啮合力为研究对象，通过对比该轮系健康齿轮与1/3裂纹故障齿轮、1/2裂纹故障齿轮的动态响应时域图，如图4所示，可以看出，健康齿轮时域图边缘是光滑的，但是随着裂纹的严重程度增加，时域信号幅值增加非常显著，出现了十分明显的幅值调制，周期性冲击信号的幅值同时也是在不断变大。

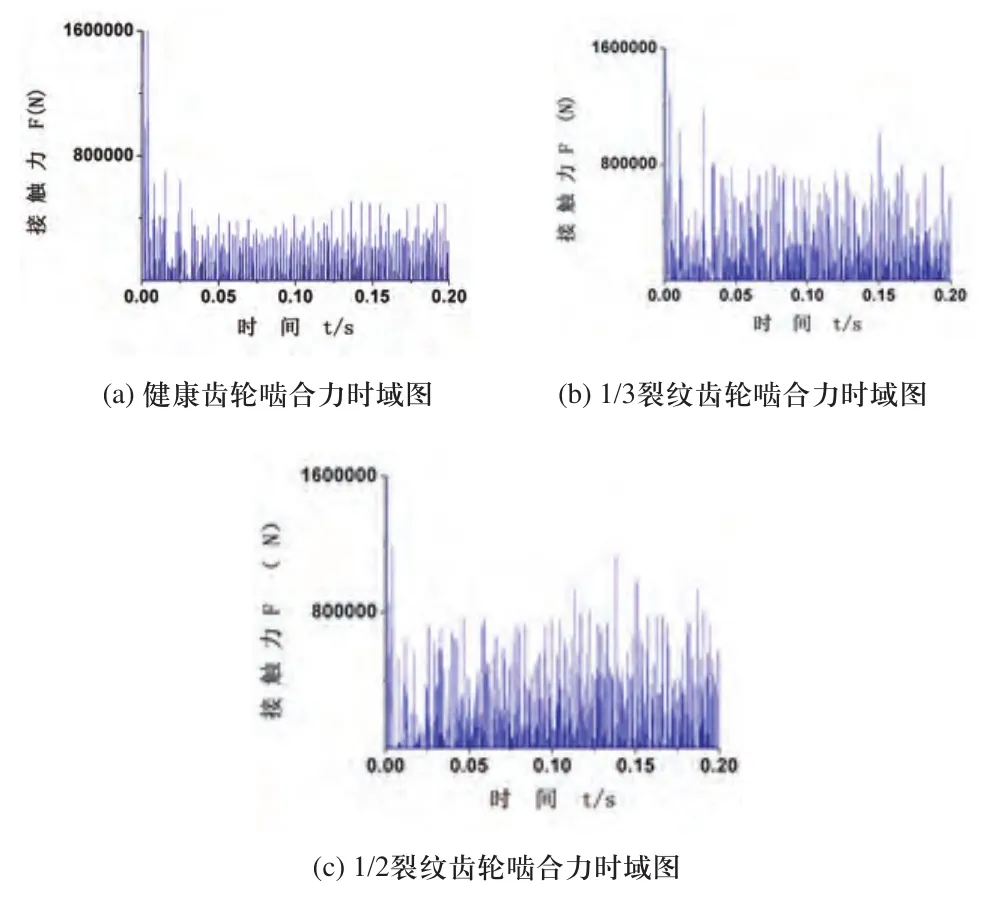
图4 采煤机摇臂高速区啮合力时域图

3.3 动态响应频域对比分析

系统轮系健康齿轮与1/3裂纹故障齿轮、1/2裂纹故障齿轮的动态响应频域图如图5所示。

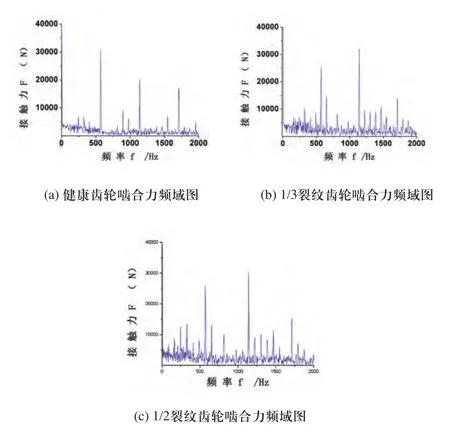
图5 采煤机摇臂高速区啮合力频域图

齿轮1、齿轮2接触力啮合频率为570Hz，与上面的频域响应曲线图的峰值频率569.55Hz一致。主频后面的两个峰值的频率值分别为1141.36Hz、1708.94Hz，在误差允许范围内，分别等于570Hz的2倍和3倍，因此视作主频的2倍频、3倍频。从图5中对比可以看出，随着裂纹故障的出现，可以看出啮合频率及其倍频周围出现大量边频带，其中前几阶倍频的边频带密度增大相对明显，且边频带幅值随着裂纹故障程度的增加而提高。为了定量地研究裂纹故障退化程度对变频带的影响，为故障诊断算法设计提供参考，采用边带主频幅值比对该变频带进行分析，该研究结果将为后续大功率采煤机故障诊断算法设计提供理论参考[7]。频用fd表示，设频率f的边带的幅值为A(f)，那么为了描述主频边带特征，引入边带主频幅值比R[7]。具体将频域响应带入式（6）计算：

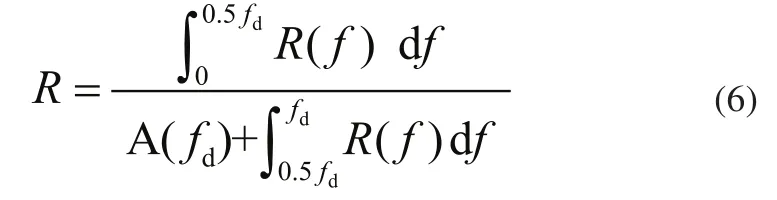
得出结果如表2所示。

表2 边频带主频幅值比

通过表2可以看出，当裂纹出现并且更加严重时，边带主频幅值比增加，并且变化很大。故可将边带主频幅值比作为大功率采煤机高速区故障监测指标，以监测齿轮裂纹状态及退化程度。

4 结论

针对大功率采煤机摇臂高速区齿轮故障高发，本文通过虚拟样机技术，建立了采煤机高速区轮系多体动力学模型。在动力学模型的基础上，分别建立了1/3裂纹和1/2裂纹的齿轮故障模型，通过系统动态响应的时域图和频域图分析，得出结论：随着裂纹的严重程度增加，时域信号幅值增加非常显著，出现了十分明显的幅值调制，周期性冲击信号的幅值同时在不断变大；齿轮裂纹故障下，啮合力边频带能量密集，密集程度随着裂纹程度增大而增加[8]，通过边带主频幅值比能够定量监测这一变化趋势。

[1]徐志鹏.采煤机自适应截割关键技术研究[D].徐州:中国矿业大学,2011.

[2]周久华,米林.采煤机摇臂齿轮箱故障与可靠性分析[J].内蒙古科技与经济,2011,14(2):107-110.

[3]张启龙,周久华,周唯嘉.对比分析大功率采煤机摇臂齿轮箱[J].煤矿机电,2012,5:126-127.

[4]陈峰华.ADAMS2012虚拟样机技术从入门到精通[M].北京:清华大学出版社,2013.

[5]周炎强.直齿圆柱齿轮及其裂纹故障的的动态特性与数值模拟[D].太原理工大学,2008.

[6]龙凯,程颖.齿轮啮合力仿真计算的参数选取研究[J].计算机仿真,2002,19(6):87-91.

[7]程哲.直升机传动系统行星轮系损伤建模与故障预测理论及方法研究[D].长沙:国防科技大学,2011.

[8]Zhe Cheng, Niaoqing Hu, Xiaofei Zhang.Crack level estimation approach for planetary gearbox based on simulation signal and GRA[J].Journal of Sound and Vibration, 2012,331 (26):5853-5863.