基于旋量法的可变形六足机器人腿部运动学分析
2015-07-07于常娟张明路刘庆玲刘欣媛
于常娟,张明路,刘庆玲,刘欣媛
(1.河北工业大学 机械工程学院,天津 300130;2.廊坊师范学院 数信学院,廊坊 065000)
0 引言
普通的仿生机器人腿部一般具有根关节、髋关节和膝关节三个转动关节,腿部末端位置如果确定,那么腿部位姿也随之唯一确定[1,2],本文突破以往六足仿生机器人运动模式单一和固定的局限,提出了一种具有变形能力的六足仿生机器人,和普通六足仿生机器人的区别是每个腿又设计了一个变形关节,从而使腿部能以不同的姿态到达同一位置,因此增加了六足机器人腿部运动的多样性和灵活性,以及对不同地形适应的能力,该机器人可根据地形的情况模仿不同动物行走的方式和姿态,如螃蟹、蜘蛛和壁虎等动物。
传统的D-H方法的局限性在于只能表示关于x轴和z轴的转动和移动,不能表示关于y轴的运动。由于该六足仿生机器人腿部具有沿y轴的移动,所以不能直接应用传统的D-H方法进行运动学建模。而旋量方法可以表示任意方向的转动和移动,且只需建立基础坐标系S和工具坐标系T两个坐标系,运算过程较D-H法简单。利用旋量理论计算机器人的雅克比矩阵可避免对运动学位姿正解求导,简化了计算,并且避免了D-H法的奇异性问题。
因此采用旋量方法和指数积公式建立可变形腿的运动模型,计算腿部的正解和逆解以及雅可比矩阵。刘亚军等运用旋量方法建立操作臂串联机构运动学模型,得到该操作臂的16组运动学逆解的解析解[3]。胡典传等利用传统D-H分析方法建立装夹机械手的运动学模型[4]。钱东海等基于旋量理论建立6自由度机器人运动学模型并利用Paden-Kahan子问题得到其逆解算法[5]。张小俊等基于旋量法对连续体搜救机器人运动学分析并计算其雅克比矩阵[6]。许晨等利用旋量理论建立多运动体航天器的运动学模型[7]。
1 可变形六足机器人本体结构
该可变形六足仿生机器人的六条结构相同腿部对称分布在机体的两侧。和普通六足机器人不同,可变形六足仿生机器人每条腿除了具有根关节、髋关节和膝关节外还有一个变形关节,这样每条腿具有四个转动关节。当变形关节的转角发生变化时可以改变腿部行走的模式,完成多运动模式行走的功能,如模拟蜘蛛、螃蟹和壁虎等不同昆虫或哺乳动物的行走模式,具有多运动模式能力有利于增强六足机器人对未知环境的适应性和可通过性。图1为六足可变形仿生机器人的样机。

图1 六足仿生机器人样机
2 建立腿部运动学模型
机器人单腿示意图如图2所示。机身1与构件2连接处有两个旋转关节根关节和髋关节,根关节1绕z轴正方向转动,髋关节2绕y轴负方向转动,构件2与构件3由膝关节3连接也绕y轴负方向转动,构件3与构件4由变形关节4连接。
2.1 正运动学分析
建立基础坐标系o-xyz,原点o在腿与机身的接触点。腿部初始位置:构件2和构件3都与x轴重叠,方向向右,构件4沿y轴正方向。构件2、构件3和构件4的长度分别为l2、l3和l4。
初始位置时四个转动关节的轴线方向和位置如表1所示。

表1 各关节的螺旋轴线方向和位置

图2 机器人单腿示意图
转动关节变换矩阵:

θi为各转动关节的转动角度,hi为各螺旋运动的节距,由于各关节没有沿各轴线方向移动,所以hi都为0。足端相对于基础坐标系o-xyz的位姿矩阵为:
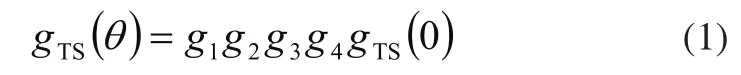
其中gTS(0)为足端在初始时刻相对基础坐标系位姿矩阵:

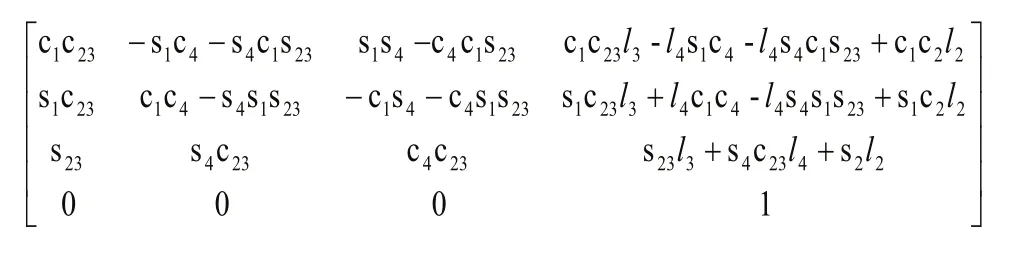
其中,p(0)为初始时刻足端在基础坐标系下的坐标。ci、si分别是 cos(θi)和sin(θi)的缩写,c23、s23分别是cos(θ2+ θ3)和s i n(θ2+ θ3)的缩写。
足端的坐标为:
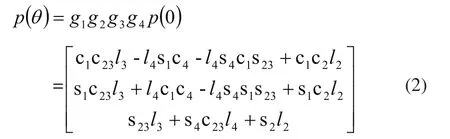
2.2 逆运动学分析
式(1)两边同时右乘gTS-1(0)得:
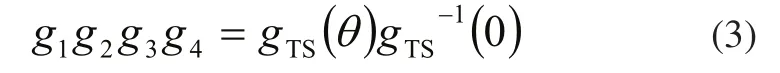
点q3同时在关节3和关节4的轴线上,式(3)两边同时右乘q3得:

解得:
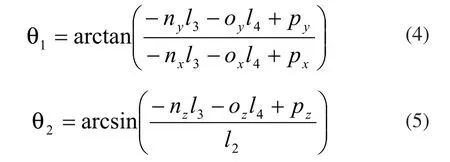
把θ1和θ2的值代入式(3)得:
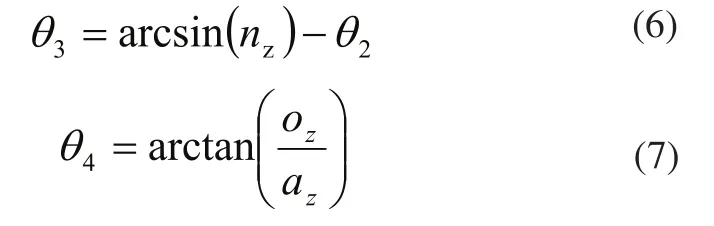
2.3 正解和逆解的验证
设 θ1= π /6,θ2= π /6,θ3= π /4,θ4= π /6;
则根据式,足端相对于基础坐标系o-xyz的位姿矩阵为gTS(θ),其中:
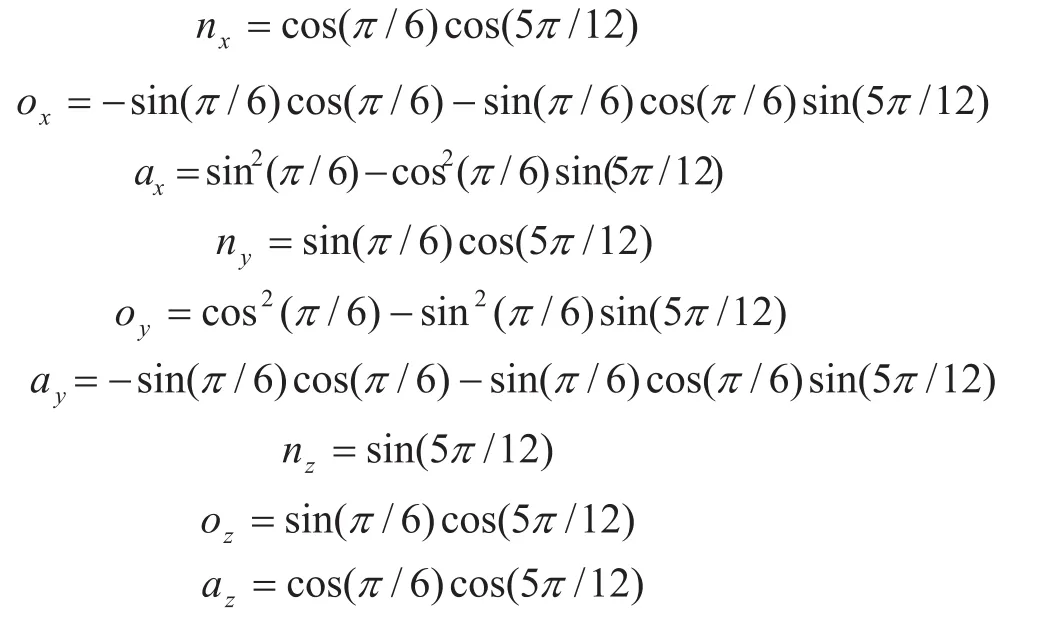
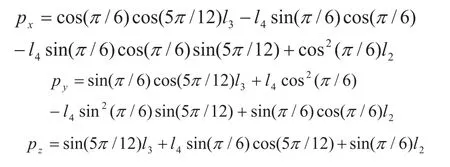
根据逆解式(4)~式(7)解得:
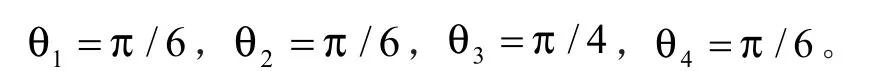
逆向运动学的输出是正向运动学的输入,说明利用旋量理论与指数积方法建立腿部运动学模型正确。
3 雅可比矩阵求解

为机器人足端瞬时空间速度(相对惯性坐标系的速度),(θ)为机器人相对惯性坐标系的雅可比矩阵。为机器人腿部各关节相对惯性坐标系的角速度。
传统方法是对正向运动学求导得到雅可比矩阵但是求导过程复杂。而利用旋量理论描述雅可比矩阵计算自然简单,并且结果有明确的几何特征。

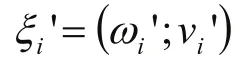
其中:

因此,不必对正解求微分就能求出机器人足端的雅可比矩阵,这大大简化了雅可比矩阵的计算量,并且避免了传统方法可能存在的奇异性问题。
四个转动关节的初始时刻运动旋量Plücer射线坐标为:

四个转动关节的当前时刻运动旋量Plücer坐标为:

六足仿生机器人腿部相对惯性坐标系的雅可比矩阵[8]。
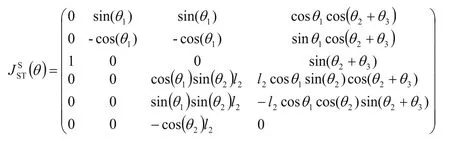
4 MAPLE仿真
机器人腿部构件的参数l1=2cm,l2=20cm,l3=15cm,l4=10cm。当各关节转动的空间角速度(相对惯性坐标系)=(10,20,10,20)时,根据式(2),机器人足端相对惯性坐标系的三个方向位移变化如图3所示。

图3 机器人足端位移变化曲线
根据式(8),得到机器人足端瞬时空间速度:
其中为足端物体坐标系相对惯性坐标系的角速度,如图4所示。

图4 足端坐标系空间角速度变化曲线
为机器人腿部最末构件上的经过惯性坐标系原点的点相对惯性坐标系的速度如图5所示。
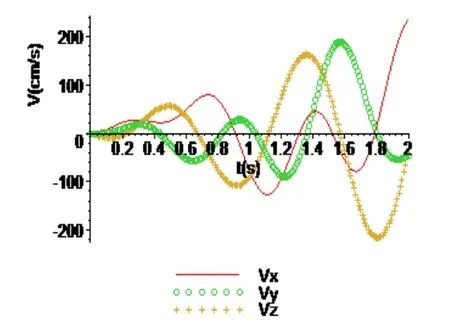
图5 足端通过惯性坐标系原点的空间速度变化曲线
5 结论
基于指数积和旋量理论为六足可变形仿生机器人的腿部建立了运动学模型,并计算得到足端位姿正解的解析解,利用经典消元理论和Paden-Kahan子问题方法计算其运动学的解析逆解。根据旋量理论推导出腿部的雅可比矩阵,并利用MAPLE软件对足端的位置和速度进行仿真,验证了运动学模型和雅可比矩阵的正确性。
[1] Donghoon Son,Dongsu Jeon, Woo Chul Nam,Doyoung Chang, TaeWon Seo,Jongwon Kim.Gait planning based on kinematics for a quadruped gecko model with redundancy[J].Robotics and Autonomous Systems,2010,58:648-656.
[2] 孟偲,王田苗,丑武胜,官胜国,裴葆青.仿壁虎机器人的步态设计与路径规划[J].机械工程学报,2010,46(9):32-37.
[3] 刘亚军,黄田.6R操作臂逆运动学分析与轨迹规划[J].机械工程学报,2012,48(3):9-15.
[4] 胡典传,顾寄南,师二产.新型装夹机械手的运动学分析与轨迹规划[J].制造业自动化,2011,33(5):100-102.
[5] 钱东海,王新峰,赵伟,崔泽.基于旋量理论和Paden-Kahan子问题的6自由度机器人逆解算法[J].机械工程学报,2009,45(9):72-76,81.
[6] 张小俊,孙凌宇,张明路,张玉娟.基于旋量法的连续体搜救机器人运动学分析[J].华中科技大学学报,2013,41(12):90-94.
[7] 许晨,陆宇平,刘燕斌,徐志晖.多运动体航天器旋量理论动力学建模与滑模控制[J].系统工程与电子技术,2012,34(12):2535-2540.
[8] 兰陟,李振亮,李亚.基于旋量理论的5-DOF上肢康复机器人雅克比矩阵求解[J].机械设计,2011,28(5):51-53,74.
