多线切割机张力控制系统的优化

张桂鹏，李 英，高 志

（华东理工大学 机械与动力工程学院，上海 200237）

0 引言

多线切割技术是一种新型的切割技术，其原理是通过切割线的往复运动，把磨料带入加工区域进行研磨切割，可一次性将材料加工成几百上千枚薄片[1]。与传统的加工技术相比，多线切割机具有生产效率高、加工精度高等优点，在硬脆性材料加工领域有很强的优势，已逐渐取代传统的加工技术，成为主流的半导体材料加工装备[2]。

多线切割机控制系统复杂，影响切割机加工精度的因素有很多，其中切割线张力的控制尤为重要。张力过大，会导致切割线崩断，造成材料的浪费；张力过小，会导致切割机加工精度降低[3]。控制多线切割机走线系统的张力是关系到生产效率、加工精度的关键技术。文献[4]采用PID积分分离算法对多线切割机的张力进行控制；文献[5]采用了一种基于相邻轴误差的多电机同步控制方法来控制张力波动。目前讨论放线辊半径、走丝换向等扰动因素以及将模糊PID控制方法应用于多线切割机的张力控制等方面的研究还比较少，本文提出了一种基于模糊PID控制的张力控制方法，并对该方法进行了仿真验证，仿真结果证明了该方法有效地优化了走线系统的张力波动。

1 走线系统运动学与动力学模型

以切割机走线系统的放线端为研究对象来分析张力波动的原因。图1为放线端结构示意图，张力控制方式为弹簧张紧。系统装有角位移传感器，将测得信号反馈给PLC，形成闭环控制。

1）运动学模型

如图1所示，张力轮在平衡位置的摆动幅度很小，可以认为张力轮线速度是沿竖直方向的，忽略摩擦力和切割线的弹性伸缩，可以得到张力控制系统的运动学方程。

图1 放线端结构示意图

根据运动学关系有：

式中：v为张力轮线速度；

v1为放线辊线速度；

v2为加工辊线速度。

张力轮在竖直方向上的位移Δx为线速度的积分：

张力轮的角位移θ为角速度的积分：

式中：w为张力轮角速度；

L为摆杆长度。

2）动力学模型

如图1所示，张力轮在平衡位置的摆动幅度很小，可以认为张力轮的运动方向是沿竖直方向的，忽略摩擦力和切割线的弹性伸缩，可以得到张力控制系统的动力学方程：

式中：T为切割线张力；

m为张力轮质量；

k为张力弹簧弹性系数。

由此可得切割线的张力表达式为：

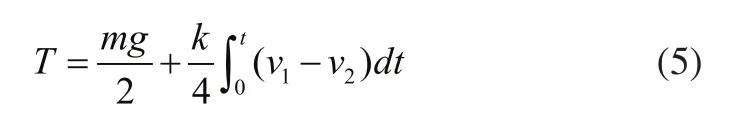
由式(5)可知，系统的张力由两个部分组成：

第一部分由张力轮的质量决定，当张力轮质量m不变时，该部分为恒定的。

第二部分由加工辊与放线辊的速度同步情况决定，因为张力弹簧的弹性系数k为恒定的。

由式(5)可以得到，控制系统切割线的张力波动是由于放线辊与加工辊速度不同步引起的，两者速度差越大，张力轮角位移越大，张力波动就越大。

2 控制系统张力扰动因素分析

针对控制系统，首先加入传统的PID控制方法，以张力轮角位移为输入，放线辊电机角速度作为输出，根据上述的运动学与动力学模型，使用Simulink进行建模与仿真并分析控制系统张力扰动因素。以多线切割机的期望线速度作为控制模型的指令输入，如图2所示。

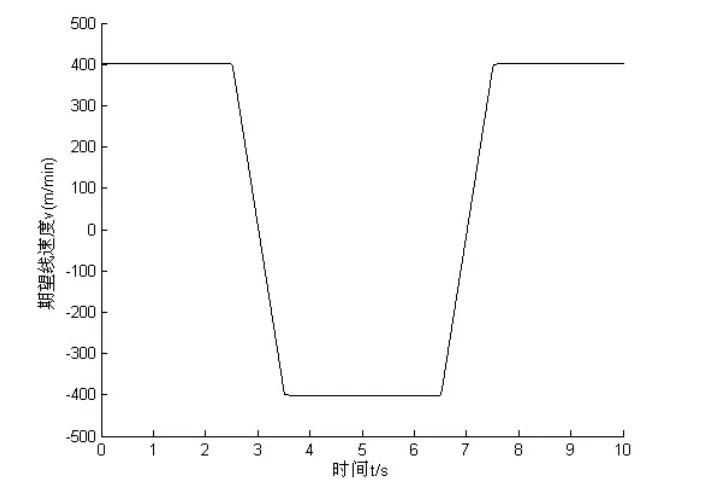
图2 期望线速度曲线

1）放线辊半径对控制系统的影响

PID控制器属于线性控制，即输入和输出之间存在线性关系。在本控制系统中，这种线性关系体可以表示为：

式中：A为常数；

w2为放线辊角速度；

对式(6)两边同时微分并乘以L：

由式(3)可知：

所以有：

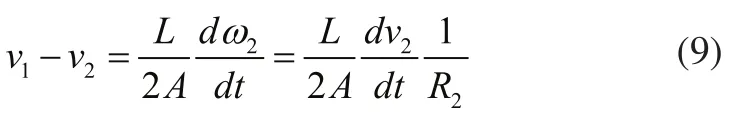
放线辊稳定工作时线速度是恒定的，因此式(9)右边除了R2项外，其他项均为定值。由此可以得到，放线辊半径越小，放线辊与加工辊线速度差越大，张力轮角位移越大，张力波动越大。图3为放线辊半径R2不同时，系统线速度差的曲线图，由图中可以看出前面的分析是正确的。

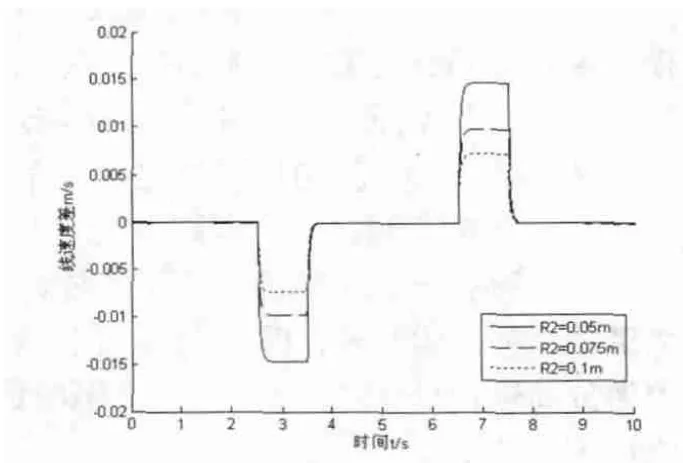
图3 R2不同时系统线速度差

在多线切割机的实际加工过程中，放线辊半径R2最小的时刻就是绕在放线辊上的切割线全部放完时，也就是放线辊的半径。放线辊半径R2取最小值时，放线辊与加工辊速度差最大，只要此时切割线的张力波动能够满足控制要求，那么加工过程中无论R2怎样变化，均能满足控制要求。因此在仿真过程中，R2始终选取最小值。

2）走丝换向对系统的影响

在切割机的实际工作过程中，走线速度变化是非常迅速的，走丝换向时间非常短，各电机的速度在短时间内不停地变化，此时会产生明显的张力波动[6,7]。采用直线变速方式时，切割线在换向时刻会发生瞬时的加速度跳变，导致系统产生很大的张力波动。为了使走丝换向能够平滑过渡，不发生瞬时的加速度跳变，采用余弦变速来替代直线变速。图4为直线变速方式下系统张力波动曲线，图5为余弦变速方式下系统张力波动曲线。

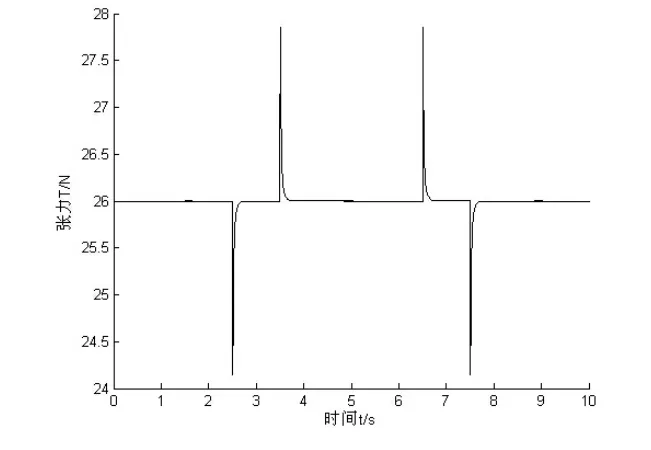
图4 直线变速方式下系统张力波动曲线

图5 余弦变速方式下系统张力波动曲线

比较图4和图5，可以看出余弦变速方式下切割线张力波动幅度更小，变速过程中的张力变化也更为连续平缓。

3 模糊PID控制器的设计

由图5可以看出，传统PID控制方法下的张力波动幅度超过了1N，控制效果并不十分理想。传统PID控制方法结构简单、易于控制，但控制精度难以达到预期的控制要求。模糊PID控制方法的精确性、鲁棒性以及可靠性等方面均优于传统PID控制方法，因此设计一个自适应模糊PID控制器，进一步优化张力控制系统[8,9]。

1）控制器的结构设计

模糊控制器采用两输入三输出结构，输入变量为误差e与误差变化率ec，误差e为张力轮的角位移θ，理想情况下张力轮应处在水平位置，加工过程中产生的任何角位移即为误差，误差变化率为dθ/dt。输出变量为PID参数调整量ΔKp、ΔKi、ΔKd，与PID参数基准量kp、kp、kp相加便得到PID参数Kp、Ki、Kd。

图6 为模糊PID控制器模型

2）控制器的算法设计

模糊控制器的输入e、ec，输出ΔKp、ΔKi、ΔKd的论域为[-5，5]。其模糊子集为{NB，NM，NS，ZO，PS，PM，PB}，各语言变量的意义为NB=负大、NM=负中，NS=负小、ZO=零、PS=正小、PM=正中、PB=正大，各变量均取三角隶属度函数。

为了保证精度，偏差语言变量E、偏差变化语言变量EC、ΔKp、ΔKi基本论域选定为[-3，3]，ΔKi的基本论域选定为[-0.5，0.5]。得到量化因子Ke=1.667、Kec=1.667，比例因子Kep=0.6、Kei=0.1、Ked=0.6。ΔKp模糊规则表如表1所示，ΔKi、ΔKi模糊规则表略。

表1 ΔKp模糊规则表

3）仿真结果及分析

切割线线速度如图2所示，系统走丝换向时间为1s,放线辊半径为0.075m，采用余弦变速方式，采用模糊PID控制器对系统进行仿真[10]，仿真结果如图7所示。

图7 模糊PID控制张力波动曲线

仿真结果表明：采用模糊PID控制器，系统的张力波动控制在0.4N左右，明显优于传统PID控制方法的1N左右，满足了系统控制精度的要求。

4 结束语

本文建立了走线系统的动力学模型，讨论了张力控制的扰动因素并进行了优化，相比于传统的PID控制方法，采用模糊PID控制方法可以把系统的张力波动控制在允许的范围内，提高了多线切割机的加工精度。

[1]王琮.半导体材料加工设备的新秀——多线切割机[J].电子工业专用设备,2004,33(4):63-65.

[2]HSU C Y, CHEN C S,TSAO C C.Free abrasive wire saw machining of ceramics[J].The International Journal of Advanced Manufacturing Technology,2009,40(5-6):503-511.

[3]徐旭光,周国安.多线切割晶体表面质量研究[J].电子工业专用设备, 2008,37(11):20-22.

[4]陈学军,吴钢华,林海波.基于PID积分分离算法的多线切割机恒张力控制研究[J].组合机床与自动化加工技术,2012,(1):81-84,92.

[5]蒋近,戴瑜兴,郜克存,等.多线切割机走线系统的张力控制[J].机械工程学报,2011,47 (5):183-186.

[6]金建华,林海波.数控多线切割机床高精度罗拉轴的关键技术研究[J].制造业自动化,2012,34(3):87-91.

[7]党兰焕,贺敬良,王学军,等.多线切割机砂浆控制系统研究[J].制造业自动化,2010,32(6):68-70,231.

[8]宋淑然,阮耀灿,洪添胜,等.果园管道喷雾系统药液压力的自整定模糊PID控制[J].农业工程学报,2011,27(6):157-161.

[9]董全成,冯显英.基于自适应模糊免疫PID的轧花自动控制系统[J].农业工程学报,2013,29(23):30-37.

[10]王中鲜.MATLAB建模与仿真应用[M].机械工业出版社,2010.