基于模糊神经网络PID的线切割张力控制系统的分析

刘 洁，魏金成，伍 林

（西华大学 电气信息学院，成都 610039）

0 引言

往复走丝线切割技术虽然有了快速的发展，但与国外的线切割技术相比，在加工精度和效率方面还是有一定的差距。往复走丝电火花线切割有成本低，能够切割厚度很大的工件等优点，故广泛应用于许多领域之中。张力控制系统是影响加工精度和效率的重要指标，实现张力值的精确控制和张力分布的均匀性控制将会大大改善工件的表面质量。本文用神经网络和模糊PID控制来实现对张力系统的控制与分析。

1 控制系统模型的建立

往复走丝线切割机床的张力控制系统主要由力矩电机、张力传感器、储丝筒、导轮、排丝机构等组成。根据电机的特性和机械控制理论相关知识，建立执行机构的数学模型，可以得出简化后的伺服电机的平衡方程式：

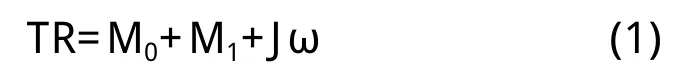
式中，T为电极丝张力，R为储丝筒半径，M0为丝与储丝筒的摩擦力矩，M1为输出转矩，J为储丝筒的转动惯量，ω(t)为储丝筒随时间变化的角速度。张力控制系统的传递函数主要由电机传递函数和张力轮传递函数组成。若不考虑张紧轮摩擦阻力的影响，张紧轮传递函数可看作一个比例环节，故张力控制系统传递函数为：

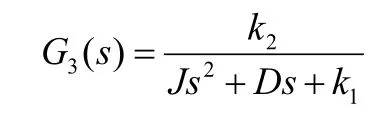
式中J为时间常数，K为常数。模糊PID控制系统的结构如图1所示。

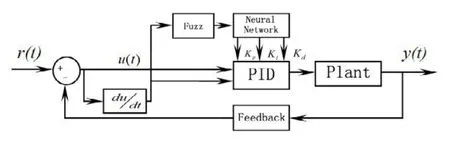
图1 PID控制结构框图

2 神经网络模糊PID控制器的设计与算法

2.1 模糊控制器的设计

神经网络模糊PID控制器是由神经网络和模糊控制器共同构成，模糊PID控制的很大优点就是不需要精确的数学模型，也可得到良好的鲁棒性能。该控制器采用离散增量式控制算法[1]，网络输出为：Kp、Ki、Kd。

PID控制规律为：

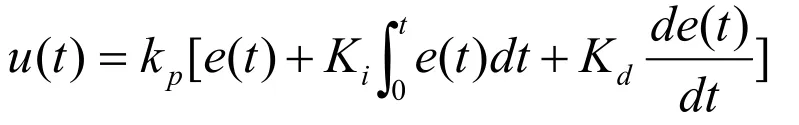
式中，Kp为比例系数，Ki为积分时间系数，Kd为微分时间系数。

误差e的模糊化变量为E，误差变化率的模糊化变量为EC，输出u的模糊化变量为U。对应的每个输入量和输出量都有七个语言值，{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}，根据操作人员的工作经验，选取49条规则，并制作模糊规则控制表。模糊集合的论域为[-5,5]。

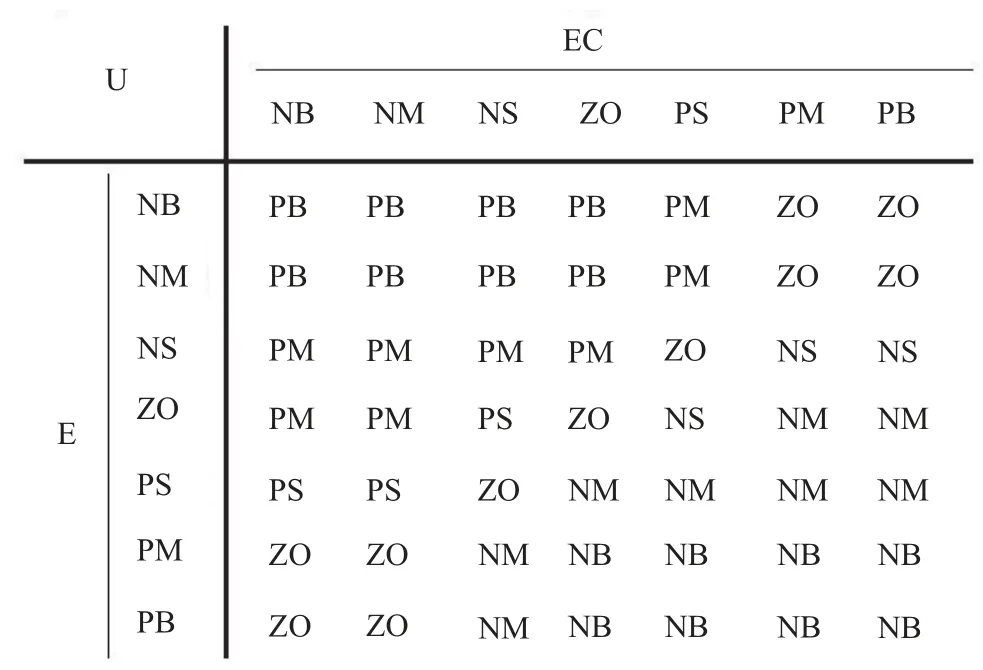
表1 模糊规则控制表

根据模糊规则控制表，利用if语句得以下模糊规则：

2.2 BP神经网络的算法学习

BP神经网络是一种前馈型神经网络，其算法是由信号的正向传播和误差的方向传播共同组成。正向传播时样本值从输入层进入，经隐含层处理，再从输出层输出，实现过程的正向传递。输出样本值与期望的值存在一定误差时，存在的误差以某种形式反向传向隐含层、输入层，并将误差逐层分配，实现误差的反向传播[2]。BP神经网络由输入层，隐含层和输出层共同组成，如图2所示。

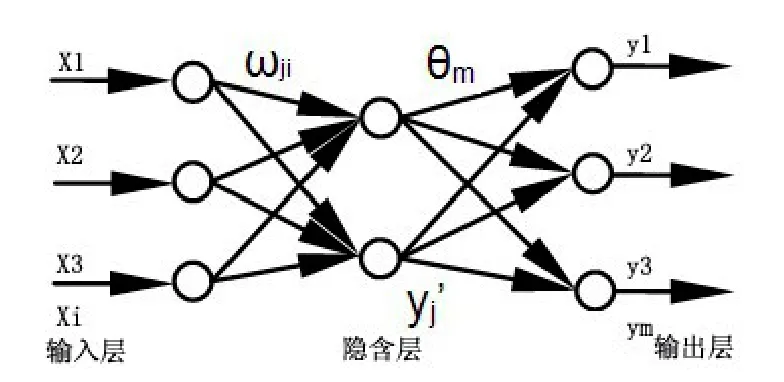
图2 BP神经网络结构图

输入：x1、x2、x3,...,xi，输入层与隐层之间的权值ωji，阈值为θj，隐层输出为yj'，阈值为θm，隐层与输出层之间权值为Tmj，输出值：y1、y2、y3,...,ym，输出节点的期望输出值为xm。则BP网络的计算公式为[3]：

隐节点的输出公式为：

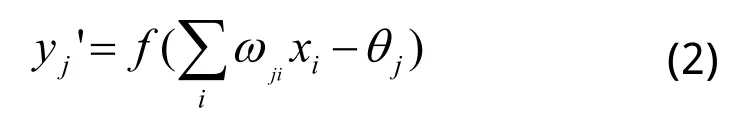
输出节点的输出公式为：

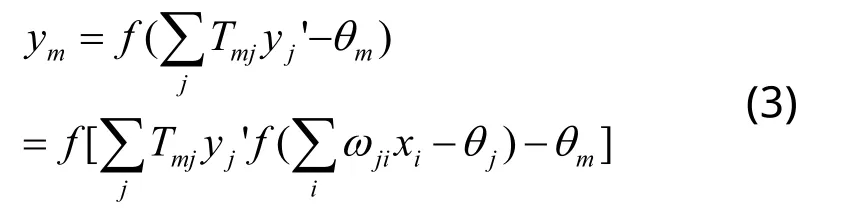
输出节点的误差公式为：

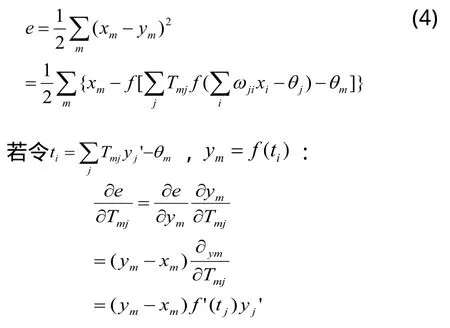
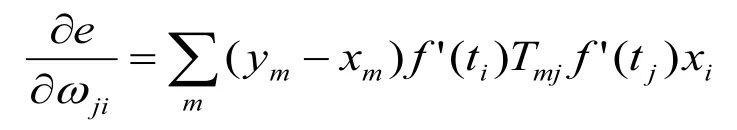
根据误差函数的梯度下降法，修正权值(ωji,Tmj)和阈值(θm,θj)；在计算过程中，通过反复修改权值和阈值，来得到合适的修正量。由可知：

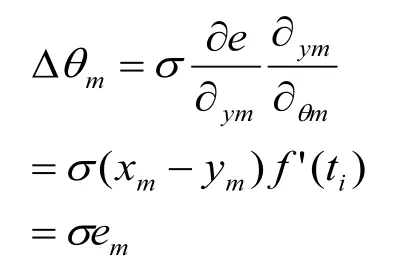
故隐含层与输出层间阈值修正公式为：

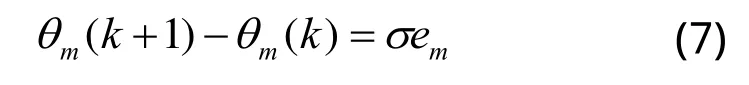
其中k为迭代次数。同理输入层与隐含层间阈值修正公式为：

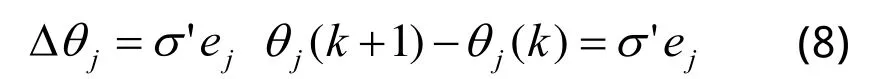
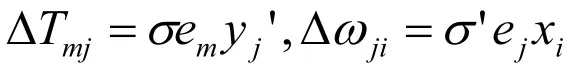
故隐含层与输出层间的权值修正公式为：

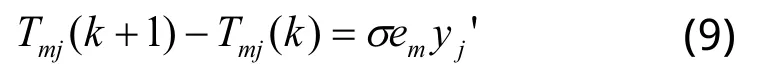
其中k为迭代次数。根据以上推算方法，可知输入层与隐含层间权值修正公式为：

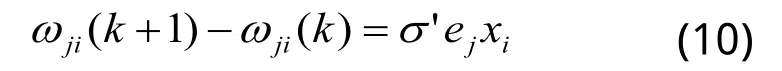
其中k为迭代次数。

神经网络模糊PID控制结合了神经网络和模糊PID控制的特点，采用模糊控制理论和对PID参数Kp、Kd、Ki的在线整定方法，实现对系统的控制。

综上所述，模糊神经网络PID控制流程算法如下[4]：

第一步：选定BP神经网络的基本结构，确定输入层、隐含层及输出层节点数，选取合适的学习率。

第二步：构建预测模型，确定输入r(t)和输出y(t)，如图2所示。

第三步：对进行u(t)模糊化处理，建立模糊PID控制规则，并确定神经网络输入参数Kp、Ki、Kd。

第四步：根据式（2）和式（3）确定各节点的输入输出值，作为BP神经网络的输入输出，神经网络的输出即为PID控制器的三个参数。

第五步：根据经典增量式PID控制方法，计算PID控制的输出。

第六步：由式（8）和式（10）修正输入层与隐含层之间的权值和阈值，由式（7）和式（9）修正隐含层与输出层之间的权值和阈值。

第七步：设置相关参数，返回第二步继续执行。

3 仿真结果分析

4 结束语

通过仿真曲线可以看出，神经网络和模糊PID结合可以实现常规控制更好的效果，且控制曲线较为光滑。如果对BP神经网络的权值和阈值进行修正和优化，系统中一些线性和非线性因素引起的的误差可得到了一定程度的抑制，使系统的整体控制性能得到了很好的实现。

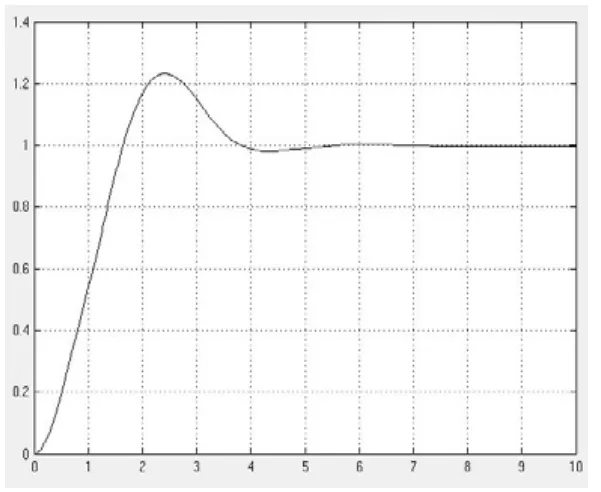
图3 常规PID控制曲线

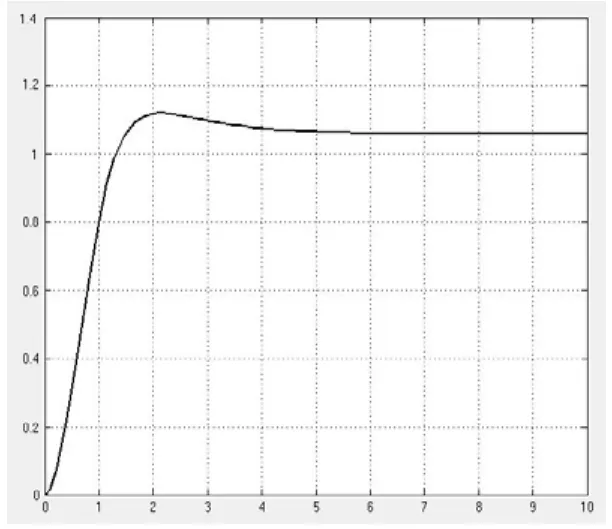
图4 模糊神经网络PID控制系统仿真

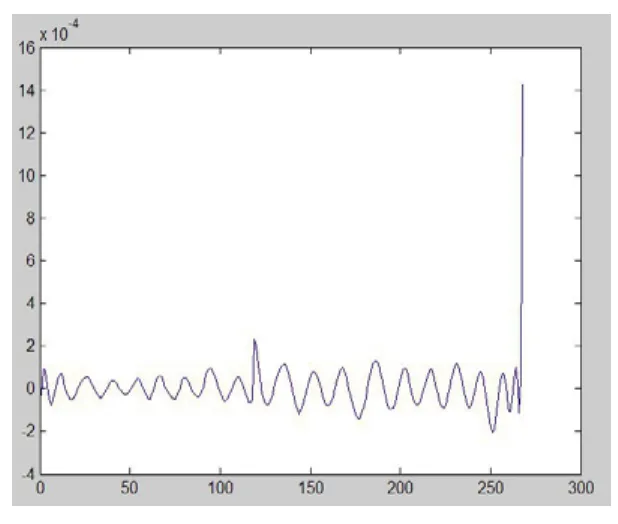
图5 神经网络训练后误差随时间变化曲线

[1]苏东海,孙占文,单光坤.基于神经网络PID控制的被动式电液加载系统[J].组合机床与自动化加工技术.2008(03).

[2]张泾周,杨伟静,张安祥.模糊自适应PID控制的研究及应用仿真[J].计算机仿真.2009,26(9).

[3]闻新,周露,李翔,张宝伟.MATLAB神经网络仿真与应用[M].北京:科学出版社.2003.

[4]董金光,魏江,李孝安,刘晓燕.基于神经网络模糊PID的足球机器人控制算法研究[J].微计算机应用.2007,28(10).