基于等距映射算法的回转机械运行状态识别理论研究

籍永建，王红军

（1.北京信息科技大学 现代测控技术教育部重点实验室，北京 100192；2.北京信息科技大学 机电工程学院，北京 100192）

0 引言

回转机械的振动信号中隐含着大量与运行状态相关的信息。合理提取所关注的信息能更好地评价其运行状态。流形学习算法是近年来比较热门的降维方法，它能够提取高维数据集中的低维流形，更直观地反应数据的本质特征。目前流形学习方法主要有主成份分析法（PCA）[1]、多维尺度分析算法（MDS）[2]、局部线性嵌入（LLE）[3]和等距映射（Isomap）[4]等。

1 等距映射（Isomap）算法

1.1 Isomap简介

等距映射（Isomap）算法是一种全局算法，建立在经典MDS的基础上，它使用比欧氏距离更好地反映数据全局几何结构的测地距来处理高度扭曲折叠的非线性流形，Isomap对数据进行降维的步骤如下[5]：

1）构建邻域图G；

对于数据集X中的所有数据点xi，(XRD⊂ )，以K最近邻或以ε为半径的球定义其邻域，离xi最近的K个数据点或者与xi距离小于ε的所有点都记作xi的邻接点。设任意两个邻接点xi与xj的边长为。

若xi与xj之间存在边，则否则接下来对所有的k=1,2,3,...,N，依次更新 (i,j)dG的值；

dG(i,j)=min{dG(i,j),dG(i,k)+dG(k,j)}，至此得到距离矩阵dG={dG(i,j)}，表示图G中每两点之间的最短路径距离。

3）构造低维嵌入空间；

1.2 算法评价标准

将残差（residual variance）作为评价降维效果的标准，残差计算公式如式（1）。

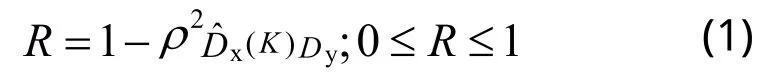
1.3 Isomap算法中参数的确定

Isomap算法中唯一的自由参数为K或邻域球半径ε，隐含参数为低维嵌入空间维数d。一般根据低维嵌入残差R来估计数据的本征维数。也就是说数据流形的固有维数d通过残差下降曲线的“拐点”来确定[7]。在邻域选择中，如果邻域太大，那么邻域中会包含流形中其他分支中的数据点，导致低维嵌入时发生错误；如果邻域太小，会将流形分割成很多不连通的区域。利用式（2）[8,9]确定最优邻域参数K。

上式表明使残差最小的邻域参数即为最优邻域参数。

2 回转机械运行状态的识别

2.1 数据采集

利用内装IC压电加速度传感器（ULT2010）采集本特利转子试验台在正常、碰磨、松动三种运行状态下的振动数据。设置采样频率为8192Hz。数据采集现场如图1所示。

图1 数据采集现场

2.2 数据处理

由于采集的振动信号中含有噪声，首先对信号进行去噪处理，然后进行归一化处理，选取13个时域特征、7个频域特征构造高维特征空间。时域指标有绝对均值、均方根值、方根幅值、最大峰值、方差、峰峰值、峭度、歪度、峰值指标、波形指标、脉冲指标、欲度指标、峭度指标，频域指标有平均频率、谐峰稳定指数，以及根据不同状态的频率特点将频域分成的5个频带[10]。利用上述指标分别构造不同运行状态振动信号的高维特征空间。

2.3 利用Isomap对高维数据进行降维处理

2.3.1 确定嵌入维数d

选取正常运行时的数据构造的高维特征空间为例。初步设定邻域参数K为8。运用Isomap对其进行降维处理。不同嵌入维数所对应的残差值如表1所示。

图2 不同嵌入维数d所对应的残差值

表1 不同嵌入维数d所对应的残差值

由表1、图2可以看出，d=2时残差值出现拐点，所以嵌入维数选为2。

2.3.2 邻域参数K的取值

选取正常运行时的数据构造的高维特征空间。设置嵌入维数d=2。运用Isomap对其进行降维处理。不同邻域参数K对应的残差值如表2所示。

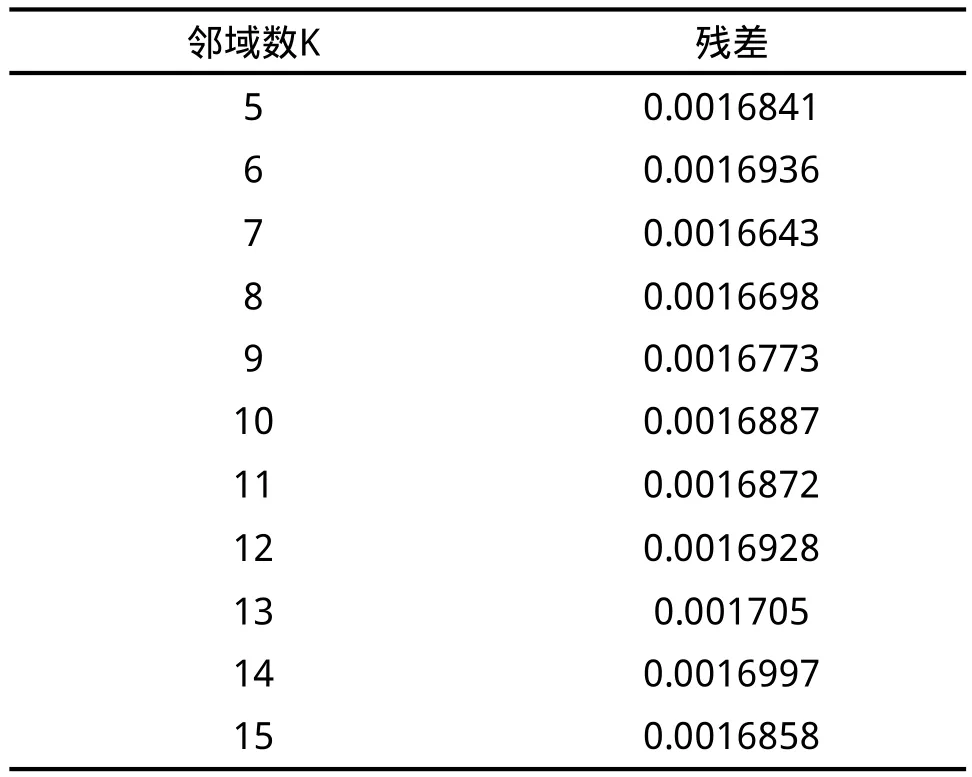
表2 不同邻域参数K所对应的残差值

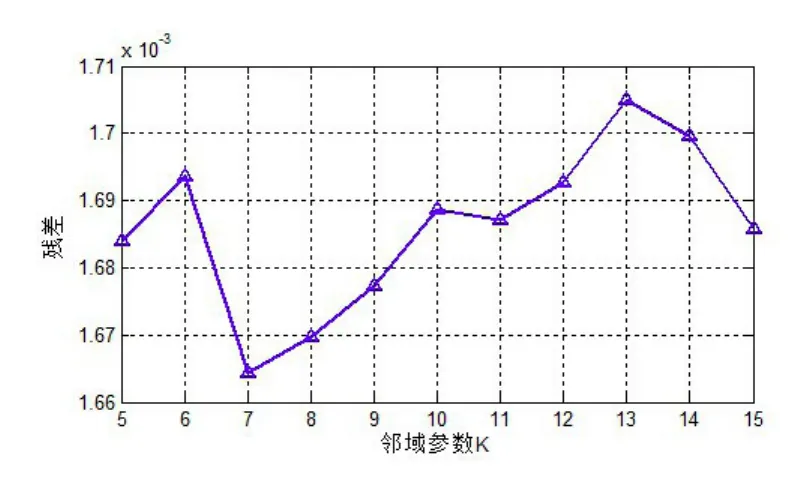
图3 不同邻域参数K所对应的残差值

由表2、图3可以看出，K=7时残差值最小，为0.0016643，所以取邻域参数K=7。

2.3.3 提取低维流形

经过以上分析，选取嵌入维数d=2，邻域参数K=7。运用Isomap分别对转子系统正常、碰磨、松动三种运行状态的振动信号构造的高维特征空间进行降维处理，提取其中的低维流形。三种运行状态对应的二维流形如图4所示。

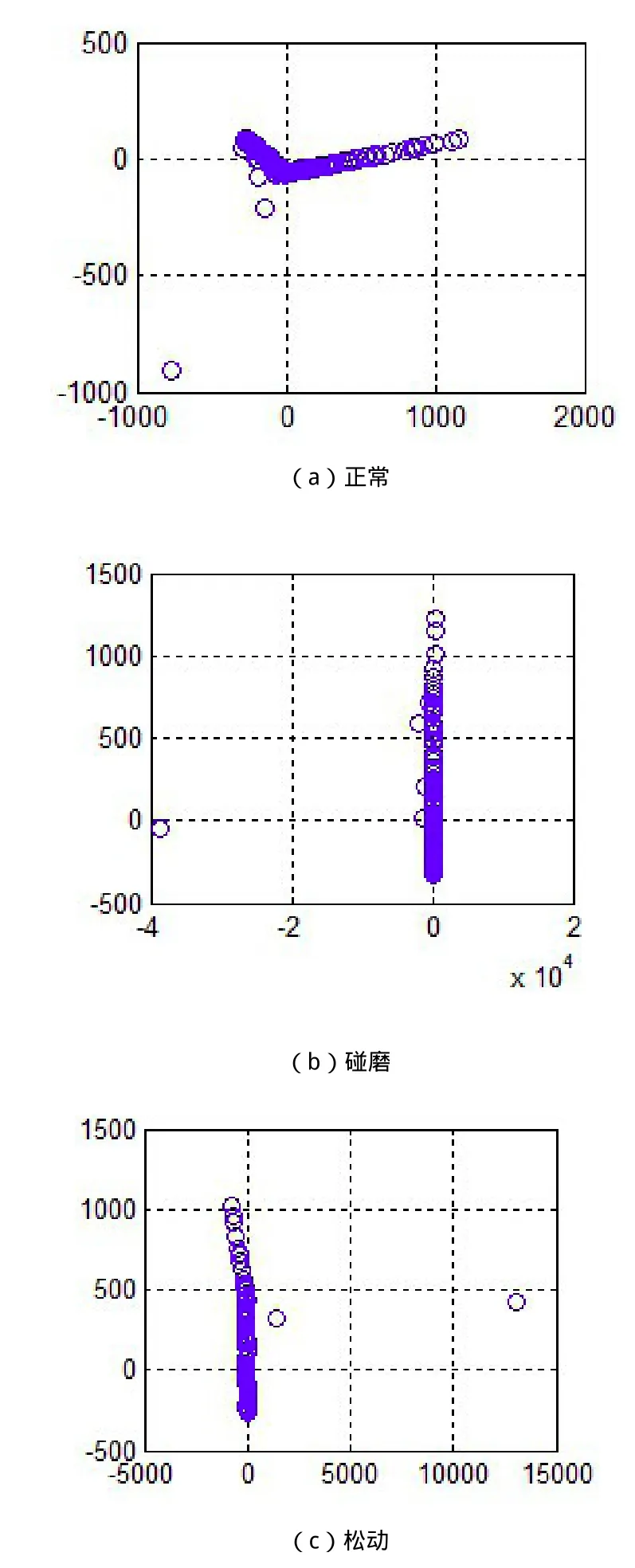
图4 降维后的二维流形图

由图4可以看出，等距映射算法能够很好的区分转子系统运行正常与故障时的低维流形，但是无法区别碰磨与松动两种运行状态。所以可以运用此方法来判别转子系统是否正常运行，但是若对故障类型进行判别，则需要做进一步研究。

3 结论

Isomap算法是一种典型的非线性流形学习方法，此算法能够提取高维特征空间的低维流形。针对回转机械运行状态的识别问题，构造振动信号的高维特征空间，并运用Isomap算法提取转子试验台不同运行状态下振动信号的低维流形，结果表明，此种方法能够很好地区分转子系统正常运行与故障运行两种运行状态，但是在具体识别何种故障时仍有缺陷，需要做进一步探究。

[1]T.Hastie and W.Stuetzle.Principal Curves[J].Journal of the American Statistical Association,1989,84:502-516.

[2]T.Cox and M.Cox.Multidimensional Scaling[M].Chapman&Hall, Londom,2001.

[3]S.Roweis, J.Saul.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290:2323-2326.

[4]J.Tenenbaum,Vde Silva, J.Landford.A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000,290:2319-2323.

[5]聂秀山,刘琚,秦丰林.基于等距映射的视频水印算法[J].计算机工程,2010,19:237-238,243.

[6]张银凤,王晅,马建峰.基于最优邻域图的等距映射流形学习算法[J].计算机工程与应用,2011,14:124-127,145.

[7]张银凤.流形学习算法的研究[D].陕西师范大学,2010.

[8]J.B.Tenenbaum,Vde Silva, J.C.Langford.The Isomap algorithm and topological stability-response[J].Science,2002, 295: 5552-5559.

[9]O.Samko,A.D.Marshall, RL.Rosin, Selection of the optimal parameter value for the Isomap algorithm[J].pattern Recognition Letters,2006,27:968-979.

[10]万鹏.基于流形学习的主轴系统故障诊断方法研究[D].北京信息科技大学,2013.