不同区域的BDS实时用户保护水平研究分析
2015-07-07张静云秘金钟谷守周王晓慧
张静云,秘金钟,谷守周,王晓慧
(1.山东科技大学,山东 青岛 266510;2.中国测绘科学研究院,北京 100039; 3.武汉大学,武汉 430079;4.中国地质大学(武汉),武汉 430074)
不同区域的BDS实时用户保护水平研究分析
张静云1,2,秘金钟2*,谷守周2,3,王晓慧4
(1.山东科技大学,山东 青岛 266510;2.中国测绘科学研究院,北京 100039; 3.武汉大学,武汉 430079;4.中国地质大学(武汉),武汉 430074)
随着GNSS的不断增加,GNSS完备性监测逐渐成为研究的热点领域。针对GNSS的完备性监测,本文提出了实时用户保护水平。为了分析BDS下不同区域的实时用户保护水平的差异,本文利用水平保护水平和垂直保护水平模型;结合四个区域的监测站的实时监测结果;对BDS的实时用户保护水平结果进行了计算分析,并验证了该算法的稳定性。
BDS;GNSS;水平保护水平;垂直保护水平;稳定性
0 引言
我国自主拥有自主知识产权的北斗卫星导航系统(BeiDou navigation satellite system,BDS)在2012年正式在亚太区域运行,它是全球卫星导航系统(global navigation satellite system,GNSS)的最有特色的GNSS。用户保护水平(horizontal/vertical protection level,XPL)是描述卫星系统完备性的一个重要指标,有效的XPL是保证卫星系统正常安全提供各项服务的一个重要内容[1-2]。XPL可以预报或监测导航系统的安全状况。如果XPL估计过大,会含有部分系统错误,降低系统完备性能;XPL估计过小,会产生部分误警信息,影响系统的正常使用,所以有效的XPL算法是保证系统有效使用的关键[3-7]。为了分析我国卫星导航系统的运行状况以及给用户提供安全方便的服务,本文利用水平保护水平(horizontal protection level,HPL)和垂直保护水平(vertical protection level,VPL)模型,开发了BDS实时XPL数据处理软件,并结合全国不同区域的监测结果计算了BDS卫星系统下的实时XPL,分析了不同区域监测结果的差异。
1 BDS实时XPL数学模型
XPL包含HPL和VPL。水平保护水平是指在过用户的真实位置的参考椭球的切平面,以用户的真实位置为圆心,能包含所有的用户潜在位置所形成的区域的一系列圆中最小圆的半径。在选定某组卫星的条件下进行自主失误率监测时,这个区域能够满足误检率和错检率的要求。在给定的失误概率下,它是卫星与用户所形成的几何形状和卫星对用户的等效距离误差的函数。垂直保护水平是指将所有用户潜在位置形成的区域,投影到过用户真实位置且垂直于过用户的真实位置的参考椭球的切平面的直线上形成的一系列线段中最长线段的一半。在选定某组卫星的条件下进行自主失误率监测时,这个区域能够满足误检率和错检率的要求[2]。
1.1 BDS实时HPL模型
HPL模型是由瑞利函数、精度因子矩阵D及HPL的误检概率PHPL等所决定。瑞利函数的公式为
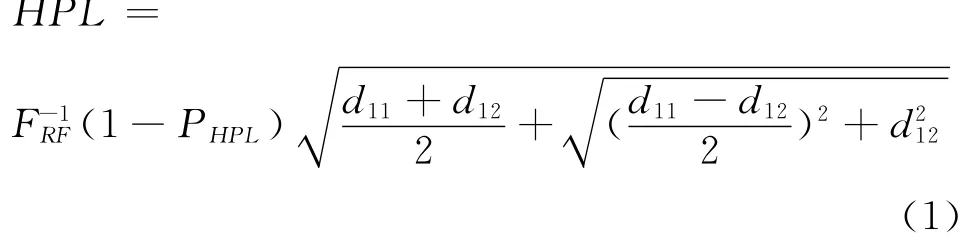
式(1)中,F-1RF为瑞利函数的反函数,PHPL为HPL的误检概率,d为精度因子矩阵D中的元素。

精度因子矩阵D是与用户等效距离误差有关的权矩阵P和与卫星有关的设计矩阵GM的函数。其中与卫星有关的设计矩阵GM由卫星的高度角和水平角决定,其定义为

式(4)中,M为当前历元的可用卫星数,En和An分别表示卫星高度角和方位角,下标n表示第n颗卫星。
卫星位置的不同对同一位置XPL的计算造成的影响不同,因而必须对不同的卫星进行加权运算(采用卫星等效距离误差进行加权)。在此采用GSSF TEAM给出的用户等效距离表进行各个卫星对用户等效距离误差的计算。表1给出的等效距离误差是在生命安全应用中对E5a和L1波段采用双频技术,不同高度角的卫星对交通工具造成的等效距离误差σi。

表1 用户等效距离误差
1.2 BDS实时VPL模型
VPL的计算模型由余误差函数和精度因子矩阵D决定。其表达式为

由于式(6)是一个反常积分函数,因此得不到其准确的反函数计算公式,在此采用反函数的方法来实现。用文献[7]提出的ltqnorm方法求解。该方法是利用相对误差的绝对值为1.15×10-9的有理函数,通过极大极小值逼近的方法而实现,其公式为
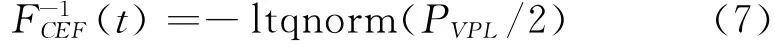
2 数据分析
基于完备性风险99.99%的要求,在非中心参数一定的情况下,利用弃真概率和纳伪概率的关系(均为0.01%),并依据单点定位水平和高程精度可以推出:用户水平示警限值(horizontal alert limit,HAL)为12 m,垂直示警限值(vertical alert limit,VAL)为20 m[2]。
2.1 数据来源
为了比较不同区域连续运行参考站(continuously operating reference stations,CORS)站的实时XPL,本文选取了4个实验区,分别是广西省(A区域)、四川省(B区域)、浙江省(C区域)、河北省(D区域),其中A区域范围20°54′N~26°24′N, 104°26′E~122°04′E,B区域范围26°03′N~34°19′N, 97°21′E~108°31′E,C区域范围27°12′N~31°31′N, 118°E~123°E,D区域范围36°01′N~42°31′N, 113°04′E~119°53′E。其中每个实验区选择3个监测站进行本次试验,每个实验区监测站编号分别为A区域(A001、A002、A003)、B区域(B001、B002、B003)、C区域(C001、C002、C003)、D区域(D001、D002、D003)。实验选择了2014-10-07~2014-10-08 (DOY279与DOY280)2 d的实时双频数据的XPL结果,数据采样率为1 s。
2.2 结果分析
在计算过程中,利用8阶Lagrange插值得出相应卫星的用户等效距离误差,并得到精度因子矩阵,进而利用上述算法分别进行HPL和VPL的计算,结果见下图1和图2。
2.2.1 HPL结果分析
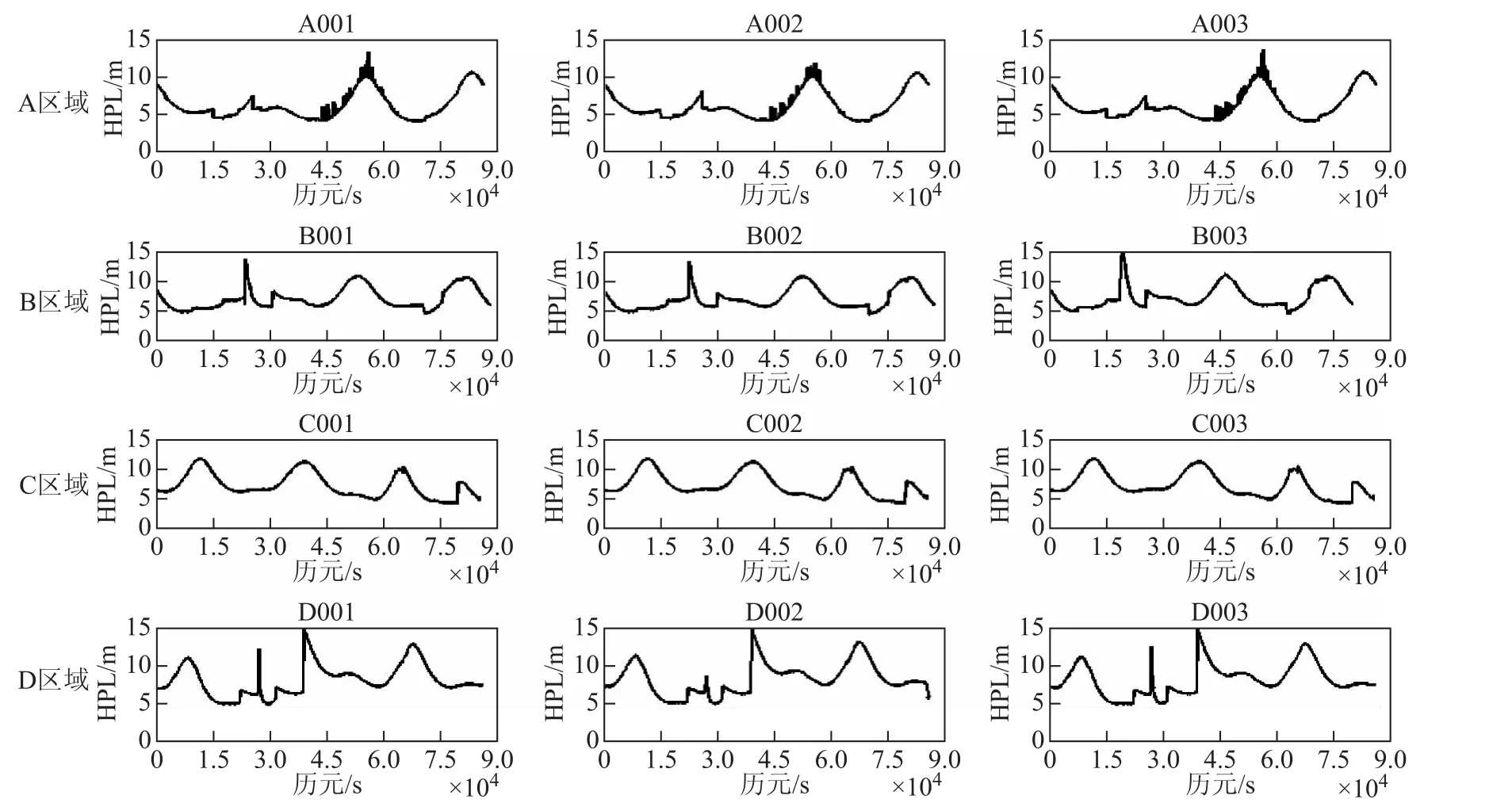
图1 年积日279的HPL结果
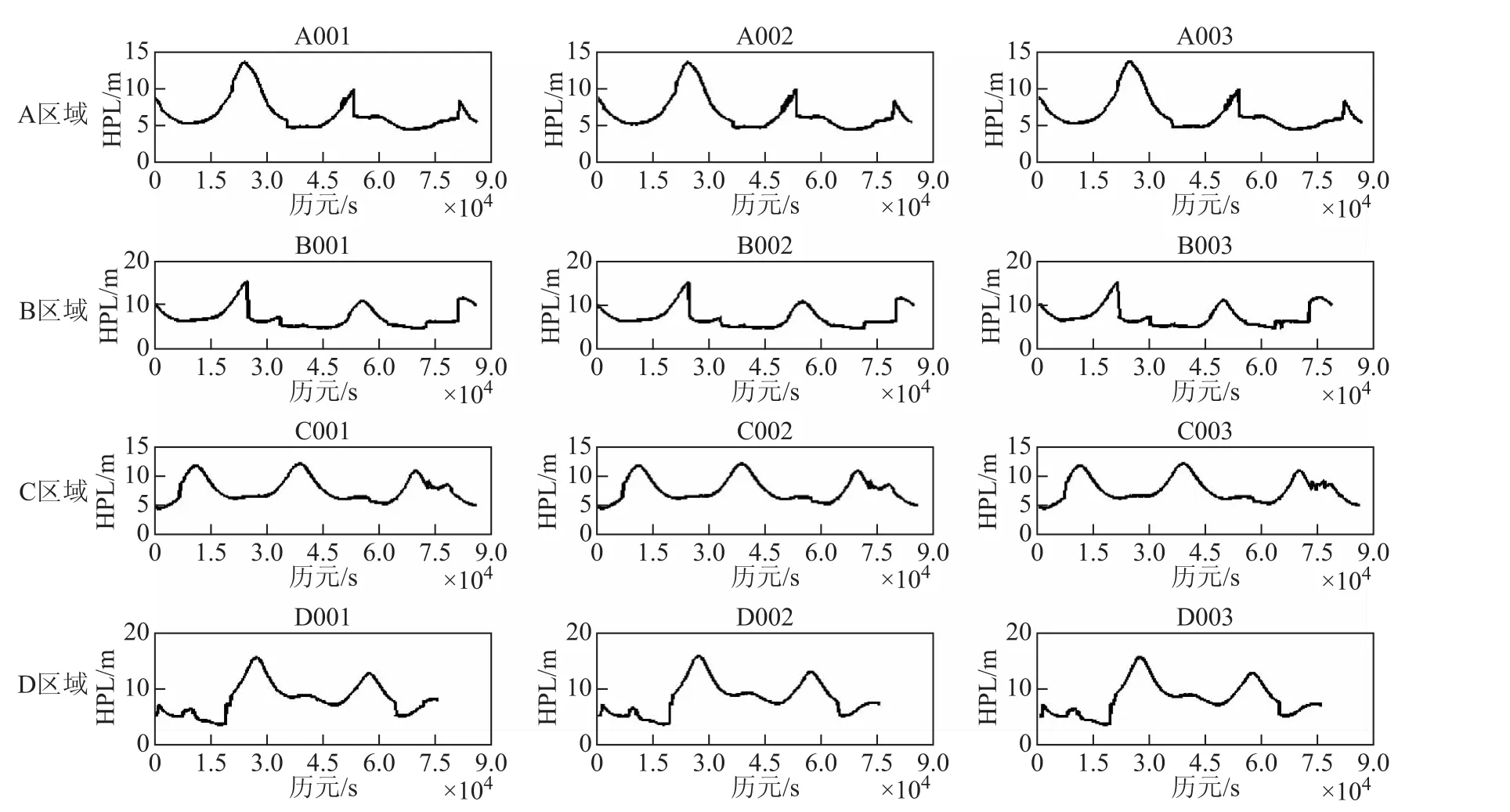
图2 年积日280的HPL结果

表2 年积日279的HPL数据统计/m
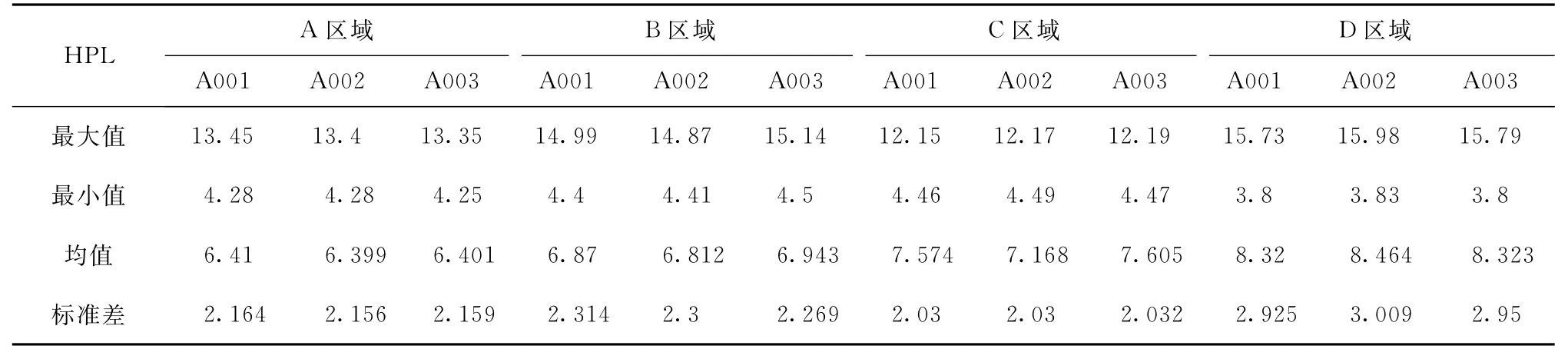
表3 年积日280的HPL数据统计/m
从表2、表3可以看出,对于A区域三个站年积日279的HPL分别为6.067、6.055、6.083,对于B区域三个站年积日279的HPL分别为6.917、6.847、7.14,对于C区域三个站年积日279的HPL分别为7.25、7.277、7.275,对于D区域三个站年积日279的HPL分别为8.063、8.244、8.109,对于A区域三个站年积日280的HPL分别为6.41、6.399、6.401,对于B区域三个站年积日280的HPL分别为6.87、6.812、6.943,对于C区域三个站年积日280的HPL分别为7.574、7.168、7.605,对于D区域三个站年积日280的HPL分别为8.32、8.464、8.323。从上述结果可以分析出,对于同一区域监测站的监测结果相对比较稳定,其变化不大,对于不同区域来说,纬度大的区域比纬度较小的区域的结果略有增大,但变化不明显;经度较大的区域比经度较小的区域的结果变化也不明显。
从图1、图2可以看出,同一区域的监测站的监测结果比较类似,由于不同区域卫星几何构型不同,不同监测站的监测结果有所差异,但是不同区域监测站的均值相近,并比较稳定。
2.2.2 VPL结果分析

图3 年积日279的VPL结果

图4 年积日280的VPL结果

表4 年积日279的VPL数据统计/m

表5 年积日280的VPL数据统计/m
从图3、图4、表4、表5可以看出,对于A区域三个站年积日279的VPL分别为9.01、9.043、9.084,对于B区域三个站年积日279的VPL分别为9.619、9.575、9.78,对于C区域三个站年积日279的VPL分别为9.85、9.98、9.86,对于D区域三个站年积日279的VPL分别为9.822、9.841、9.845,对于A区域三个站年积日280的VPL分别为8.972、8.97、9.034,对于B区域三个站年积日280的VPL分别为9.113、9.078、9.12,对于C区域三个站年积日280的VPL分别为9.93、10.05、9.94,对于D区域三个站年积日280的VPL分别为9.6、9.6、9.59,从上述结果可以分析出,对于同一区域的监测站的监测结果相对比较稳定,其变化不大,对于不同区域来说,纬度方面,纬度大的区域比纬度较小的区域的结果略有增大,但变化不明显。经度方面,经度较大的区域比经度较小的区域的结果变化也不明显。
从标准差来看,对不同区域不同站的结果的标准差都比较稳定,并且趋于1~2 m。从每个站的最大值和最小值来看,对于BDS系统,每一天中只有极少数历元的HPL结果大于12 m和20 m的限差要求,不同经度同一纬度区域标准差差异很小;对于不同纬度区域的标准差,随着纬度越大,标准差越大;但是都稳定在1~2 m,可知该算法对于不同的卫星组所计算出的HPL具有稳定性。
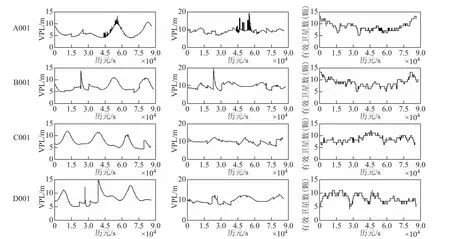
图5 年积日279有效卫星数统计图与HPL、VPL的关系
从图5可以看出,当有效卫星数越少时,计算出来的实时HPL和实时VPL的值偏大。纬度越大可利用的卫星数越小,这是由于我国自主研制的BDS卫星导航系统,在高纬度区域可观测到的GEO卫星数较少。因为随着纬度的增大,GEO卫星高度角越低,有效利用的卫星数越少,所以高纬度区域,计算出来的实时HPL、VPL结果离散性比低纬度区域略有偏大,但都比较稳定。同一组观测卫星下,VPL值在连续历元间的变化也比较小,大部分在厘米级,只有卫星组中的卫星发生变化时才会出现分米级的跳跃。
综上所述,在卫星发生故障或者卫星几何构形不能用于某种服务时,HPL的计算值就会大于HAL的限值,此时发出的某种示警信号是有效和值得相信的。虽然VPL的波动范围较大,但在同一组观测卫星下,VPL值在连续历元间的变化也比较小,大部分在厘米级,只有卫星组中的卫星发生变化时才会出现分米级的变化。并且从同一区域的监测站可知,由于卫星的几何构型类似,所以计算出来的XPL结果差异很小。
3 结束语
(1)对于不同区域的监测站和不同区域监测到的卫星组,同一区域的不同观测站的实时监测结果很接近,利用上述算法计算出的实时HPL和VPL的均值稳定在6~7 m与8~9 m,验证了该算法的稳定性。
(2)在同一组卫星下,相邻卫星历元间,计算出的实时HPL和实时VPL值的变化都在厘米级甚至在毫米级,只有卫星组中的卫星发生变化时才会出现分米级的跳跃。
(3)不同经度同一纬度区域标准差差异很小;不同纬度区域的标准差,随着纬度越大,标准差越大,但都稳定在1~2 m。
由此可知,该算法能够满足完备性理论中的各项要求,能够实时的监测出卫星的完备性指标是否满足要求,这样就能用于预报和监测导航系统的安全状况。
[1] 党亚民,秘金钟,成英燕.全球导航卫星系统原理与应用[M].北京:测绘出版社,2007.
[2] 秘金钟.GNSS完备性监测理论与应用[M].北京:测绘出版社,2012:138-145.
[3] BLOMENHOFER H,EHRET W,SU Hua,et al.Sensitivity analysis of the Galileo integrity performance dependent on the ground sensor station network[EB/OL].(2014-01-05)[2015-05-12].http://navpos.com/Publications/ION-GNSS-2005_Blomenhofer_etal_Galileo_Sensitivity_Analysis.pdf.
[4] WU T,PECK S.An analysis of satellite integrity monitoring improvement for WAAS[C]//The Institute of Navigation. Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GPS. Manassas,Virginia:The Institute of Navigation,2002:756-765.
[5] CURTIS A.SHIVELY,NILES R,et al.Performance and availability analysis of a simple local airport position domain monitor for WAAS[J].Navigation,2006,53(2):97-108.DOI:10.1002/j.2161-4296.2006.tb00376.x.
[6] OEHLER V,LUONGO F.The Galileo integrity concept[C]//The Institute of Navigation.Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GNSS.Manassas,Virginia:The Institute of Navigation,2004:604-615.
[7] OTAEGUI O,URQUIJO S,ROH MER G.Real time fast acquisition based on hardware FFT for a GPS/EGNOS receiver [C]//The Institute of Navigation.Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GNSS.Manassas,Virginia:The Institute of Navigation,2004:66-75.
[8] MEDEL C H,VIRGILI L P,GARCIA A M,et al.SISA computation algorithms and their applicability for Galileo integrity[C]//The Institute of Navigation.Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GPS.Manassas,Virginia:The Institute of Navigation,2002:2173-2184.
[9] 谷守周,秘金钟,党亚民.GALILEO完备性系统中XPL算法研究[J].大地测量与地球动力学.2010,30(2):104-108.
[10]杨鑫春,李征航,吴云.北斗卫星导航系统的星座及XPL性能分析[J].测绘学报.2011,40(增刊):68-72.
Research and Analysis on BDS Real_time XPL in Different Areas
ZHANG Jingyun1,2,BEI Jinzhong2*,GU Shouzhou2,3,WANG Xiaohui4
(1.Shandong University of Science and Technology,Qingdao 266510,China; 2.Chinese Academy of Surveying and Mapping,Beijing 100039,China; 3.Wuhan University Wuhan 430079,China; 4.China University of Geosciences(Wuhan),Wuhan 430074,China)
With the continuous increase of GNSS.Completeness monitoring is a hotspot of GNSS research field.For a completeness monitoring of GNSS,this paper presents the real-time horizontal/vertical protection level.In order to analyze the difference of real time horizontal/vertical protection level of the BDS in different regions.In this paper,using the horizontal protection level and vertical protection level model.using real-time monitoring results of CORS stations in four regions,calculated and analyzed real-time horizontal/vertical protection level results of BDS satellite system,and verify the stability of the algorithm.
BDS;HPL;VPL;stability
P228
A
2095-4999(2015)04-0016-06
2014-10-18
国家自然科学基金(41304030),科技部863计划(2013AA122501),地理空间信息工程国家测绘地理信息局重点实验室经费资助项目(201301),北斗分析中心(GFZX0301040308-06),科技部科技支撑计划课题(2012BAB16B01),海岛(礁)测绘技术国家测绘地理信息局重点实验室资助项目(2013B01),四川省测绘地理信息局科技项目(J2014ZC01)。
张静云(1989—),男,四川南充人,硕士生,研究方向为GNSS精密定位和数据处理。
秘金钟(1975—)男,河北衡水人,研究员,博士生导师,博士,主要从事GNSS高精度定位理论和应用研究。
张静云,秘金钟,谷守周,等.不同区域的BDS实时用户保护水平研究分析[J].导航定位学报,2015,3(4):16-21,49.ZHANG Jingyun,BEI Jinzhong,GU Shouzhou,et al.Research and Analysis on BDS Real_time XPL in Different Areas[J].Journal of Navigation and Positioning,2015,3(4):16-21,49.
10.16547/j.cnki.10-1096.20150404
