三近点角间变换的级数展开式

高端阳,李厚朴,边少锋

(海军工程大学导航工程系,武汉 430033)

三近点角间变换的级数展开式

高端阳,李厚朴,边少锋

(海军工程大学导航工程系,武汉 430033)

针对偏近点角、真近点角和平近点角之间数值变换十分困难的问题,为实现近点角间的直接变换,借助计算机代数系统Mathematica,提出了一种幂级数法,推导出它们之间变换的级数展开式,并将式中系数统一表示为轨道偏心率的幂级数形式,且扩展至偏心率的8次方。本文首先阐述方法的原理,最后通过算例分析验证,结果表明对于偏心率小于0.05的卫星轨道,该方法导出的公式计算精度优于10-5″,可供实际使用。

卫星轨道;偏近点角;平近点角;真近点角;计算机代数系统

0 引言

偏近点角、真近点角和平近点角是描述卫星运动时常用的三种近点角,在卫星星历计算[1-2]、航天器轨道确定[3-4]时经常遇到它们之间的变换问题。偏近点角和平近点角之间的变换即经典的Kepler方程解算是解决这一问题的关键,国内外学者对此经行了深入研究,取得了丰富研究成果[5-12]。总的看来,Kepler方程的解法主要有迭代法和直接法两种[5]。迭代法方面,常用的方法是Newton迭代法[6],对于收敛的迭代过程,只要迭代足够多次,就可以使结果达到任意精度,但对初值的选取要求比较高,且每次都要计算导数值。为克服Newton迭代法存在的不足,有学者提出采用Steffensen迭代法来求解椭圆轨道下的Kepler方程,以提高计算效率和收敛速度[7-9]。虽然迭代法在数值计算的精度上有一定优势,但这种方法在进行理论分析时不甚方便,不能直接表达各近点角之间的关系。为此,文献[10]给出了基于Bessel函数的Kepler方程级数解法,文献[11-12]给出了Kepler方程直接解的四元素表示,导出了小偏心率椭圆轨道下的真近点角近似方程。值得注意的是,以往研究主要集中在偏近点角和平近点角之间的变换,对于这两种近点角和真近点角之间的变换研究较少,而且部分推导过程由人工完成,展开的项数不高。鉴于此,本文在深入分析三种近点角间数学关系基础上,借助具有强大符号运算功能的计算机代数系统Mathematica[13-14]进行了新的推演,导出了偏近点角、真近点角和平近点角间变换的级数展开式,并设计算例分析了展开式的计算精度。

1 偏近点角、真近点角和平近点角的定义

图1 真近点角和偏近点角几何关系

如图1所示,O为椭圆的一个焦点(地球质心),S为卫星在轨道上的位置,r为卫星向径,N为升交点,f为真近点角,P为近地点。以椭圆中心为圆心,椭圆长半径a为半径的辅助圆,且过S 作x轴的垂线交于H,延长SH交辅助圆于S,连接S′,E为x轴与O′S′夹角,即偏近点角。

由图1可知向径r的坐标为

2 偏近点角、真近点角和平近点角间变换的级数展开式

2.1 偏近点角和平近点角间变换的级数展开式

式(9)的右端只含有E,是M的隐函数,可以利用隐函数的求导法则,将其展开成cos M的幂级数。当然,这一过程由人工来做,可能令人难以忍受,甚至不可能完成。但由计算机代数系统来做,由于求导数的过程比较机械,却是可以胜任和完成的。为使展开过程简明些,不妨再引入一新变量:

略去推导过程,在Mathematica计算机代数系统下依次求得f(t)关于t的1至8阶导数,a1, a2,…,a8依次为各阶导数在t=sin e处的值。因

2.2 偏近点角和真近点角间变换的级数展开式

由式(7)可得

2.3 平近点角和真近点角间变换的级数展开式

使用式(26)需要经过两步计算方可完成变换,计算过程较为繁琐。为简化计算,可将上式中的变量E消去,得到由平近点角M计算真近点角f的直接展开式。该过程人工推导非常繁琐,借助Mathematica强大的符号运算功能,在e=0处将f展开为e的幂级数形式,取至e8项可得

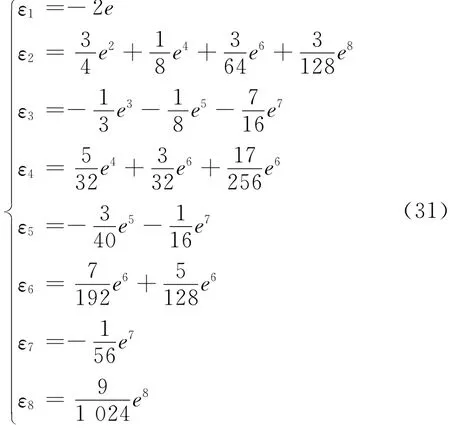
3 误差分析

为说明本文导出的级数展开式在小偏心率e= 0.01、e=0.1、e=0.2(一般认为e>0.2为大偏心率)下的精度,进行了误差分析。基本思路是:取定偏近点角E0,分别代入式(8)、式(20)可得平近点角和真近点角的理论值M0、f0,将M0分别代入式(18)、式(27)可得偏近点角和真近点角的变换值E1、f1,将f0分别代入式(24)、式(30)可得平近点角和偏近点角的变换值E2、M1,将E0代入式(21)可得真近点角的变换值f2。将上述变换值分别与理论值E0、M0、f0相减可得相应展开式的计算误差,分别记为ΔE1、Δf1、ΔM1、ΔE2、Δf2。计算误差的大小可以反映展开式的精确与否。计算结果见表1～表4。

表1 e=0.01时的计算误差

表2 e=0.05时的计算误差

表3 e=0.1时的计算误差

表4 e=0.2时的计算误差

由表1～表4可以看出,本文导出的级数展开式计算精度在e=0.01时优于10-10(″),在e=0.05时优于10-5(″),在e=0.1时优于10-3(″),在e= 0.2时优于0.1(″)。因此,本文导出的级数展开式完全可以满足偏心率e小于0.05的卫星轨道计算精度要求。

4 结束语

本文通过构思独特的数学分析,建立了适合计算机代数系统Mathematica分析和推导的三种近点角间变换的数学模型,推导出了它们之间变换的级数展开式。本文研究表明:

(1)由于轨道偏心率影响,近点角间变换的级数展开式涉及较多复杂的数学推导,计算机代数系统强大的数学分析功能为解决这类问题提供了有力的帮助。本文推导过程预示Mathematica在解决卫星轨道其他数学分析问题中也有着良好的应用前景。

(2)本文导出的级数展开式是三种近点角间的直接关系式,式中系数统一表示为轨道偏心率的幂级数形式。利用该式可实现三种近点角的直接变换,避免了繁琐的迭代运算,为进行卫星轨道相关理论分析提供了依据。

(3)算例分析表明,对于轨道偏心率e小于0.05的卫星,本文导出公式的计算误差优于10-5″,可以满足卫星轨道确定所要求的计算精度。由于希望卫星对全球有均匀的信号辐射强度、均匀的覆盖面积和均匀的卫星通过时间,大部分全球导航卫星轨道形状是近圆形的。因此,本文导出的技术展开式可直接应用于全球导航卫星轨道分析和确定。

[1] 李庆海,崔春芳.卫星大地测量原理[M].北京:测绘出版社,1989.

[2] 李济生.人造卫星精密轨道确定[M].北京:解放军出版社,1995.

[3] 郗晓宁,王威.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003.

[4] 刘林.航天器轨道理论[M].北京:国防工业出版社,2000.

[5] 岳锦海,黄天衣.Kepler方程解法的评估[J].紫金山天文台台刊,1997,16(3):164-174.

[6] 顾晓勤.椭圆轨道上航天器位置的一种计算方法[J].电子科技大学学报,2003,32(6):635-637.

[7] 束雄英,李红.Kepler方程的一种迭代加速算法[J].航空计算技术,2005,35(1):41-44.

[8] SHARMA J R.A composite third order Newton-Steffensen method for solving nonlinear equations[J].Applied Mathematics and Computation,2005,169:242-246.

[9] 刘兰冬,苏新卫.一种求解椭圆轨道Kepler运动超越方程的高效迭代法[J].长江大学学报(自然科学版),2010,7(4): 1-3.

[10]COLWELL P.Bessel functions and Kepler’s equation[J].The American Mathematical Monthly,1992,99(1):45-48.

[11]VRBIK J.Solving Kepler’s problems[EB/OL].[2014-08-18].http://www.mathematica-journal.com/2011/07/solvingkeplers-problem/.

[12]顾晓勤,谭朝阳.椭圆轨道真近点角的级数计算方法[J].应用数学和力学,2005,26(11):1301-1306.

[13]边少锋,许江宁.计算机代数系统与大地测量数学分析[M].北京:国防工业出版社,2004.

[14]李厚朴,边少锋,钟斌.地理坐标系计算机代数精密分析理论[M].北京:国防工业出版社,2015.

The Series Expansions of Transformations between Eccentric,Mean and True Anomalies

GAO Duanyang,LI Houpu,BIAN Shaofeng
(Department of Navigation,Naval University of Engineering,Wuhan 430033,China)

Aiming at computational difficulties between eccentric,mean and true anomalies,in order to realize the direct transformations between them,the series expansions of their transformations are derived using the power series method with the help of computer algebra system Mathematica.Their coefficients are expressed in a power series of the orbital eccentricity and extended up to eighth-order terms of the orbital eccentricity.The principle of the method is described firstly,and verified by the numerical examples.The results show that the precision of these expansions is higher than 10-5″when the orbital eccentricity is smaller than 0.05,which could satisfy practical application.

satellite orbit;eccentric anomaly;mean anomaly;true anomaly;computer algebra system

P228

A

2095-4999(2015)-04-0057-05

2014-10-18

国家自然科学基金项目(41274013;41471387)。

高端阳(1995—),男,湖南邵阳人,本科,主要从事卫星导航研究。

高端阳,李厚朴,边少锋.三近点角间变换的级数展开式[J].导航定位学报,2015,3(4):57-61.GAO Duanyang,LI Houpu,BIAN Shaofeng.The Series Expansions of Transformations between Eccentric,Mean and True Anomalies[J].Journal of Navigation and Positioning, 2015,3(4):57-61.

10.16547/j.cnki.10-1096.20150411