动态速度的计算题解析

熊飞娥

物理这门学科是为了帮助人类解决一些实际问题而逐步建立起来的自然科学，随着科技的发展、社会的进步，物理已经深入人类生活的各个领域。初二教材“物体的运动”这章，要求学生掌握速度的计算题，很多教师以为学生数学已经学了关于速度的计算，现在物理只要加上公式和书写规范就可。其实不然，这部分有很多联系现代科技和生活的动态速度的计算题，学生不容易理解，很容易混淆各物理量之间的对应关系，从而计算错误或无从下手。下面我就几个历年的物理中考题为例来分析。

例1：一门反坦克炮瞄准一辆坦克，开炮后1s看到炮弹击中坦克爆炸，3.5s后听到爆炸声，若当时的声速是340m/s，求炮弹的飞行速度。

正确的解题过程是先分析出声音传播的路程就是反坦克炮和坦克之间的距离，那就要先算出声音传播的路程，问题就出在这里，有三分之二的学生把声音传播的时间对应成3.5s，从而算出坦克和反坦克的距离为3.5s乘以340m/s，其实3.5s还包括炮弹飞行的Is。所以，应该用声音传播的时间25s乘以340m/s，得出声音传播的路程，这个路程也就是炮弹飞行Is对应的路程，最后算速度。这个题目要求学生分清楚炮弹和声音两个动态对应的时间和路程，就可以正确解题了。

例2：（2014年大庆中考题）超声测速仪向障碍物发射时间极短的脉冲超声波，根据接收到的反射信号时间关系可以测量物体速度。如图所示，测速仪B向迎面匀速行驶的汽车A发生两次脉冲波的时间间隔为4.5s，发射第一个脉冲后1.4s后收到反射信号，发射第二个脉冲后0.4s收到反射信号，则汽车行驶的速度是多少？（超声波在空气中传播的速度为340m/s）

题目出来后不到三分之一的学生能正确把题目解出来。其实大部分学生解不出来题目的原因是不能完全理解题意，这时教师要和学生一起分析题意。

分析：求汽车的速度必须知道其行驶的距离和相应的时间。测速仪第一次发出超声波时，经过了0.7s到达了汽车处，而信号从汽车处返回测速仪，也行驶了0.7s的时间；在第二次发出的信号，在与汽车相遇返回到测速仪时，超声波行驶了0.2s；这两次汽车与测速仪的距离差就是汽车行驶的距离，再找出行驶这段距离所用的时间，测速仪第一次发出超声波，运动了0.7sA'和汽车相遇，0.7s在4.5s内，要用4.5s减掉0.7s，当测速仪发出第二次超声波完毕后，超声波向汽车运动了0.2s遇到汽车，这0.2s没有在4.5s肉，所以要加上0.2s。求出汽车运动的距离和时间，利用速度公式即可得解。

教师要想办法走进学生的思维世界，感知他们的思维和他们的困惑，才能解决他们存在的思维障碍，从而帮助他们解决问题，这样既能增长学生的智慧，也能培养他们的情感、态度和价值观，大大地激发学生内在的学习动机。例题2明白之后，接着请学生们看看例题3和例4，结果果然出乎意料，大部分同学能快速正确分析题意并给出正确的答案。

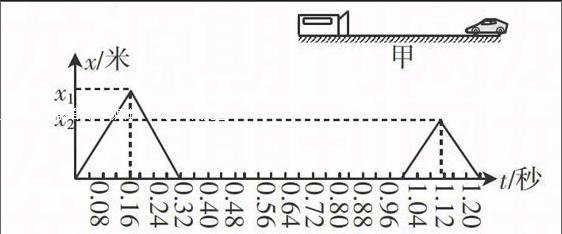
例3：（2013年绍兴中考题）交通部门常用测速仪来检测车速。测速原理是测速仪前后两次发出并接收到被测车反射回的超声波信号，再根据两次信号的时间差，测出车速，如图甲。某次测速中，测速仪发出与接收超声波的情况如图乙所示，x表示超声波与测速仪之间的距离。则该被测汽车速度是（假设越声波的速度为340m/s，且保持不变）（

）

动态速度计算加图像的分析竟然一半以上的同学读完题目后能正确得出结论。当然，我观察到三分之一的学生还是比较茫然。

分析：如果能确定超声波第一次与汽车相遇的地点4和第二次与汽车相遇的地点B之间的距离SARS，并能得到此过程所用的时间，其实这段路程对应的时间是关键。根据速度计算公式就能得到汽车行驶的速度，分析完写出下面的解题过程，帮助部分没有完全理解的学生。

由图像可知：超声波第一次从测试仪发出到与汽车相遇的地点A，经过的时间为t1=0.32s/2=0.16s，超声波通过的距离为S渡=v渡=340m/s x0.16s=54.4m。

超声波第二次从测试仪发出到与汽车相遇的地点B，经过的时间为t2=0.24/2=0.12s，超声波通过的距离为S渡2=v渡t2=340m/sx0.12s=40.8m，所以AB之间的距离为SAR=S波j-S波2=54.4m-40.8m=13.6m；测试仪发出的超声波两次间隔时间为Is，且测试仪第一次发出超声波记为0时刻，则超声波第一次从测试仪发出到与汽车相遇的地点A，经过的时间为0.16s；超声波第二次发出的时间为Is末，超声波第二次与车相遇在B点的时刻应该是ls+0.12s=1.12s，汽车从A点到B点行驶的时间是t=1.12s-0.16s=0.96s，所以汽车行驶的速度为v=s/t=1 3.6m/o.96s=14.17m/s，故选D。

通过以上动态速度的计算题的透析，让学生亲自经历发现问题、分析问题、突破关键，从而自己解决问题的过程，这才是高级的、具有创造性的学习活动。明代陈献章说得好：“小疑则小进，大疑则大进，疑者觉悟之机也。一番觉悟，一番长进。”