运用现代信息技术激发学生学习数学的兴趣
2015-07-05肖玉敏
肖玉敏
创新是北京精神的精髓,创新是发展思维的动力,作为新时代的数学教师,在数学教学中既要注重传统教法,更要有创新精神,不断变换思考问题的角度,跳出习惯思维的圈子,便会增长教学的才干。现行中学教科书已经增添了“探究”,这一环节充分发挥了学生的思维的新颖性、独特性,同时增加了思维的自由度。现代化信息技术,让静止的几何图形“动”起来,学生思维“活”起来,调动了学生学习积极性,为学生的想象力插上了创新的翅膀。下面,谈谈我的一些做法。
一、充分利用现代化信息技术,让静止的几何图形“动”起来,学生思维“活”起来
例如,《义务教育课程标准实验教科书》八年级下册第57页第11题,我根据学生实际将题目进行改编,然后引导学生利用轴对称变换的方式进行探究。
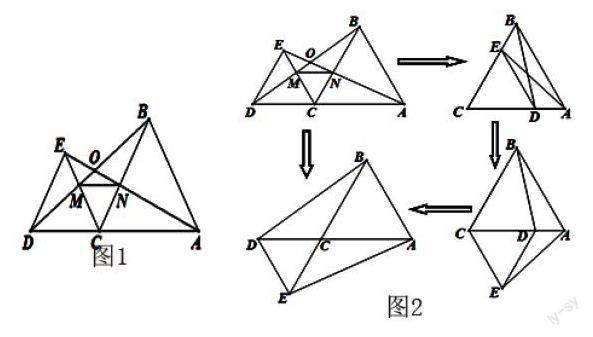
已知:如图1,C是AD上一点,分别以CD、CA为边做等边△EDC和△BCA,AE交CB于点N,BD交CE于点M,AE、BD相交于点O.
求证:MN//DA.
探索过程:(如图2)
在图1中,将△EDC沿过点C垂直于AC的直线翻折;然后将△EDC沿着AC翻折;再将△EDC沿过点C垂直于AC的直线翻折。分别探索各图中存在几对全等三角形?EA与DB两条线段是否相等?你还有什么新的发现?目的是让学生进一步认识“运动变化中的不变量”。
一石激起千层浪,好奇心促使很多學生课后效仿教师的思路,用几何画板自制了此图形,并使其运动变化起来,外地发现使同学按不住内心的激动,到校后,有的同学及时找到我与我一起探究,有的同学迫不及待地向大家展示自己的“发明创造”。
通过探索,同学们学着用类比的方法归纳出了两条结论:第一,具有一个公共顶点的两个边数相同的正多边形,在公共端点处的两对相等邻边的另一端点的交叉连线相交构成的两对对顶角中,总有一对对顶角的度数等于此正多边形的内角的度数。第二,具有一个公共顶点的两个边数相同的正多边形,在公共端点处的两对相等邻边的另一端点的交叉连线长度相等。这就是现代信息技术的魅力,让我们的学生体会了“运动中的不变量”,感受了数学美和图形变换在数学研究中的作用,初步掌握了探究途径和探究方法,激发了同学们学习和探究的兴趣,提高了学生的幸福感。每天,我和孩子们一起读书,一起讨论。面对我的学生,面对学生每天的每个个案,我微笑,我幸福。
二、充分利用现代信息技术调动学生积极性,培养学生的创新意识和能力
由于教育环境的充分敞开,教师不再是学生获取知识的唯一源泉,而应成为学生研究信息交汇的枢纽,成为交流的组织者和建议者。教学不再是简单的知识灌输,或者知识的移植过程,而是真正意义上的学生为主体,教师为主导的交互作用过程。凡是学生自己能够探索得出的,教师决不代替;凡是学生能够独立发现的,教师决不暗示,使自己真正成为课堂教学的组织者、指导者和参与者。探究性活动强调师生分享彼此的思考、见解和知识,交流彼此的情感和理念,求得新的发现,实现教学相长。
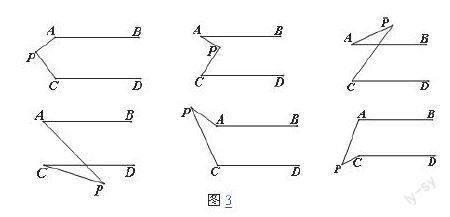
例如,某同学利用几何画板自制课件,对平行线有关问题进行研究。他认为在AB//CD的前提下,任意拖动P点,可以得到一组图形(如图3),对题目的几种探索中,∠P、∠A、∠C的大小关系各不相同,但这三个角之间始终存在着密切的联系。在探索过程中,感受到了发现的喜悦,因此他认为利用好现代信息技术可以从多角度对教材中基本图形进行认识、再思考,可以使学习变得更加轻松和有趣。
在初三的总复习中,当我们复习平行线知识时,我将以某同学发现的形式呈现给大家,此时,某同学面带自豪,自信心不用言表,当时的数学课是下午第一节,暖洋洋的太阳光使得本身就疲惫不堪的学生们已迷迷糊糊。然而,此时好奇心与好胜心交织在一起,竟然起到了难以想象的效果。所有的人的眼睛都瞪得出奇的大,注意力出奇的集中,发言出奇的踊跃,解题方法出奇的多,思维出奇的灵活,因此,此题的复习使大家都得到了意外的收获——创新意识在有意无意中得到了培养,我也从中得到了启发。
引导学生进行探究性学习是一个循序渐进的鼓励与诱导的艺术,教师需把目光投向未来,又应善于在今天安装“启动装置”。在和谐的教学气氛中,只有当学生能够主动地提出问题,才能涉及到“为什么”的问题。学生的主动学习会促使认识不断的产生质的飞跃,探究意识和探究能力也会慢慢增强。
