浅谈中考中常见的几类最值问题的解决方法

刘晓霞

一、二次函数最值的求法

二、几何形最值问题

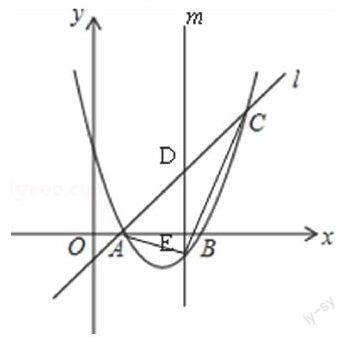
例1（2013·新疆）如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）.

（1）求抛物线的解析式；

（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；

（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标。

分析：

（1）利用待定系数法求二次函数解析式解答即可；

（2）利用待定系数法求出直线AC的解析式，然后根据轴对称确定最短路线问题，直线AC与对称轴的交点即为所求点D；

（3）根据直线AC的解析式，设出过点E与AC平行的直线，然后与抛物线解析式联立消掉y得到关于x的一元二次方程，利用根的判别式△=0时，△ACE的面积最大，然后求出此时与AC平行的直线，然后求出点E的坐标，并求出该直线与x轴的交点F的坐标，再求出AF，再根据直线l与x轴的夹角为45°求出两直线间的距离，再求出AC间的距离，然后利用三角形的面积公式列式计算即可得解。

本题考查了二次函数综合题型，主要考查了待定系数法求二次函数解析式，待定系数法求一次函数解析式，亮点在第三问，解法一利用轴对称确定最短路线问题，联立两函数解析式求交点坐标，利用平行线确定点到直线的最大距离问题.解法二构造二次函数表示出线段DE及的S△AEC函数关系式，利用二次函数顶点坐标公式求面积的最大值。

三、商品利润最值问题

例2 （2010武汉）某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满。当每个房间每天的房价每增加10元时，就会有一个房间空闲。宾馆需对游客居住的每个房间每天支出20元的各种费用。根据规定，每个房间每天的房价不得高于340元。设每个房间的房价每天增加x元（x为10的正整数倍）。

（1） 设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；

（2） 设宾馆一天的利润为w元，求w与x的函数关系式；

（3） 一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？

答：一天订住34个房间时，个房间时， 宾馆每天利润最大，最大利润是10880元。

本题根據实际问题构造二次函数，并非仅通过二次函数的顶点坐标公式求最值，而是在给定自变量取值范围内，根据二次函数的性质及图像求二次函数的最值。