稀疏条件下基于散射点估计的SAR切片超分辨重建

1 引言

SAR通过距离向发射宽带信号，方位向增加相干积累获得高的2维分辨率成像，在资源勘探，军事目标识别等方面有着重要的应用。受到硬件成本，技术等方面的限制，通过“软方法”获得超分辨图像引起了学者们的广泛关注。

目前，雷达图像的超分辨方法主要沿用光学图像超分辨方法，大致上分为3类：插值法，重建法和学习方法。插值法一般不需要引入先验信息，使用线性或者非线性的方法对相邻像素进行插值，但是简单的插值往往会导致图像过于平滑或者产生振铃效应与伪边缘。重建法引入先验信息，模拟图像降质的逆过程，从低分辨图像中恢复高分辨图像，其中最具代表性的是正则化方法与贝叶斯框架下的最大后验概率法，二者本质上是等价的。Sun等人[1]探索图像局部梯度先验信息，并将其应用到图像的超分辨重建上，Villena等人[2]在贝叶斯框架下使用1范数正则化方法对图像进行超分辨重建，先验信息的引入使得重建法能够恢复更加丰富的高频信息，得到更好的视觉效果，但是当放大倍率超过4时，容易产生类似于水彩画的伪边缘[3]。文献[4]最早提出了基于样本学习的超分辨重建方法，其主要思想是利用图像块之间的相似性，从低分辨图像块中估计对应的高分辨图像块样本，然后重构高分辨率图像。相比插值法和重建法，学习法能够获得更多的细节信息，当放大倍率超过4时仍能获得较高的图像质量，但是学习法对训练样本的要求高，且抗噪声能力较弱。

在压缩感知(Compressed Sensing, CS)理论的启发下，基于稀疏表示的超分辨方法受到了人们的广泛关注[5- 8]。基于稀疏表示的超分辨重建法利用图像在特定域下的稀疏表示作为先验信息，对图像进行超分辨重建，该方法可以理解为加入稀疏先验的正则化重建方法。Yang等人[9,10]对基于稀疏表示的超分辨学习法进行了较深入的研究，基于稀疏表示的超分辨方法的核心问题在于寻找具有广泛稀疏表示的域(超完备字典)，许多学者在超完备字典构造方面进行了研究[9,11,12]，除此之外，学习法还需要高质量的学习样本(虽然学习法能够获得丰富的细节信息)。

受到多方面因素的影响，SAR切片的高分辨率样本严重缺乏，小训练样本使得基于学习的超分辨方法不能体现其优势，因此本文主要研究重建法获得高分辨率SAR切片相关问题。Cetin等人[13]对SAR切片的分辨率增强问题进行了较为深入的研究，其本质还是使用稀疏先验与平滑先验正则化方法对点目标或区域目标进行增强。然而，当分辨率变化时，目标散射参数可能会发生变化，并且研究表明[14]，由于SAR成像系统参数未经相关优化，基于稀疏先验的l1正则化不能够获得足够稀疏的解，分辨率提高不明显。本文在稀疏表示框架下，基于散射中心理论[15]与SAR成像模型，通过散射点参数估计，重建超分辨图像，并对算法的性能进行分析。

2 基于稀疏表示与散射中心理论的超分辨重建

2.1 SAR成像模型

SAR发射线性调频脉冲信号，点目标回波经距离-多普勒，线频调变标，频率变标[16]等成像算法处理后，得到回波信号sr可表示为距离向和方位向的两个sinc函数的乘积。若雷达照射范围内存在Q个散射点，则经成像处理后的sr( x, y)表示为

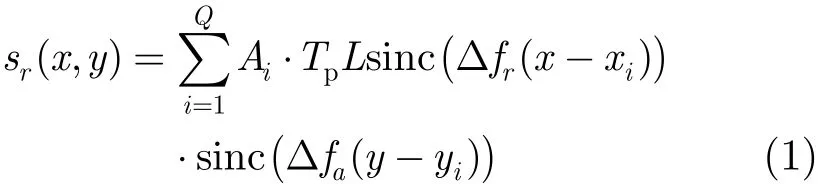
式中，x,y分别为距离向和方位向，Tp为脉冲宽度，Δfr,Δfa分别为信号带宽与方位多普勒带宽，L为合成孔径长度，Ai, xi, yi分别为第i个散射点的幅度，距离向和方位向参数。将式(1)写成矩阵形式并考虑噪声：

2.2 感兴趣目标区(Region Of Interesting, ROI)超分辨重建

基于稀疏先验的SAR图像超分辨问题是寻找图像X的最稀疏解，即求解式(3)

式(3)为无确定解析式(Non-determined Polynomial, NP)困难问题。压缩感知理论表明[18]，D满足等距约束(Restrictrd Isometry Property, RIP)和列不相干条件且x足够稀疏时，式(3)的解唯一，用l1范数代替l0范数可以达到等价稀疏的解。

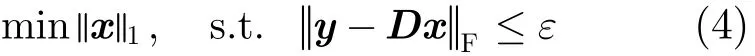
式(4)相当于一个加入稀疏先验的去模糊过程。然而大部分实际情况下，SAR系统参数与采样方式并未经过相关优化，因此D往往不具备等距约束与不相干条件[14]，式(4)代替式(3)不能够获得的等价的稀疏解*

X，该情况下可能存在两种情况，一是获得的解不够稀疏，对噪声抑制不充分，二是强制解*X稀疏，这样会对有用信号产生抑制，因此重建效果并不十分理想。

ROI在SAR切片中是稀疏的，散射中心理论认为目标的散射特性可以由少数的散射中心表示，反映到图像幅度上即少数几个中心点的散射强度显著大于其他背景散射强度。

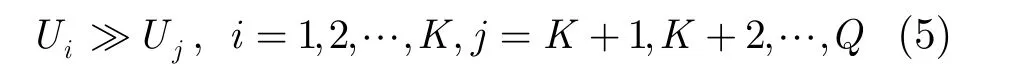
结合SAR成像模型，可通过式(6)重建高分辨率图像GK。

3 基于散射点参数估计的NP问题迭代求解算法

从数学的角度，式(6)仍为NP问题，然而K的正整数约束使这个特定的NP问题的求解变得相对简单，下面介绍如何通过参数估计的方法完成式(6)的迭代求解。

3.1 松弛法求解非线性最小二乘估计

若散射点数目K是已知且固定的，式(6)可以转化为K个散射点参数的NLS估计问题。则第k个散射点参数估计可表示为

Rk是关于的凸函数，对求偏导数，并令其为零，得

将式(8)代入式(7)，得

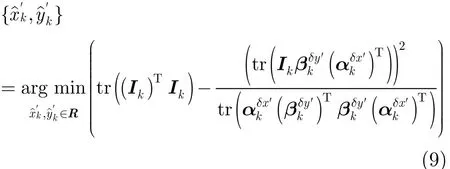
松弛法[19]可以完成K个散射点参数的估计，松弛法一次只让一个散射元参数变化，当存在多个散射点参数需要估计时，首先固定其他散射点参数，估计单个散射点参数，然后进行松弛迭代，直至收敛。

3.2 NP问题的求解

前面介绍了散射点参数的NLS估计问题，这一小节将分析如何利用估计得到的参数完成式(6)的求解。不难证明，松弛法得到的参数为 NLS估计且截断误差RK为关于K的递减序列。因此式(6)所对应的超分辨重建问题可以转化为寻找最小的K，在满足截断误差约束条件下，对K个散射点参数的NLS估计与重建。图1给出了SAR切片ROI超分辨重建的流程图。

图1 ROI超分辨重建流程图

4 算法仿真与性能分析

4.1 不同超分辨方法仿真比较

本节使用TerraSAR-X实测数据对本文所提算法进行仿真验证，并与双立方插值与l1正则化超分辨方法进行比较。图2为德国TerraSAR-X在国际标准时间2007年10月9日获取的一景直布罗陀海峡的图像。在该图像中，舰船ROI表现为强亮点，部分目标尾迹清晰可见。

图2 直布罗陀海峡的TerraSAR-X图像

人工截取舰船切片并进行1倍双立方插值，将动态范围归一化并进行局部放大，得到切片S1, S2(128×128像素)。图3，图4给出了双立方插值，l1正则化及本文方法所获得的S1, S2重建图像。正则化方法模糊算子为3 dB带宽为2.5像素的2维sinc函数，正则化参数为0.4。本文方法

接下来以空间分辨率和目标杂波比(Target to Clutter Ratio, TCR)对SAR图像质量进行评价。空间分辨率的具体估算过程为，在图像目标区域寻找每行每列的峰值点，然后从峰值点向两边寻找差值大于3 dB的最近点，再通过插值运算，得到3 dB带宽所对应的像素数目。目标杂波比对应用来衡量目标在背景杂波中的凸显程度，以dB的形式定义：

式中，T为目标区域，C为杂波区域。表1列出了不同方法获得的超分辨的空间分辨率与TCR指标值。

图3 S1超分辨重建及局部放大

图4 S2超分辨重建及局部放大

表1 不同超分辨重建方法的指标值

分析表1中空间分辨率数据，l1正则化方法能够提升SAR图像的空间分辨率，需要有模糊函数与稀疏条件作为先验信息。本文算法对SAR图像的空间分辨率提升较大，类似于l1正则化方法，本文算法需要以SAR成像模型与稀疏条件作为先验，本质上二者条件是等价的。从数据上看，本文算法相比双立方插值和l1正则化方法能够获得更高的空间分辨率，这是通过散射点参数估计实现的，并且所用sinc函数的3 dB带宽越小，重建图像的空间分辨率越高。然而，空间分辨率似乎比散射点估计时所用的3 dB带宽更大一些，仔细研究原因有二：其一，旁瓣抑制导致了主瓣的展宽；其二，图像中部分sinc函数主瓣或旁瓣交叠，导致空间分辨率降低。表1中的TCR数据反映了对不同超分辨算法对噪声的抑制能力，稀疏约束使得l1正则化与本文方法都能够获得相当高的TCR值。然而正如第2节中描述的，l1正则化方法未能充分抑制较强的尾迹杂波部分，即重建图像不足够稀疏，相比之下，本文算法对尾迹杂波抑制较为充分；而双立方插值未引入先验信息，导致其对杂波的抑制能力不强。

4.2 估计精度分析

从4.1节分析看，除了运算量之外，似乎是3 dB带宽越小越好，实际上一定如此么？本节从理论与仿真角度分析算法对噪声的稳健性，并且阐述3 dB带宽不能取得太小的原因。

考虑噪声对算法性能的影响，需要分析噪声对散射点位置与幅度估计的影响。散射点位置估计式(9)的非线性使得性能分析变得困难，将式(9)右端在处近似展开。

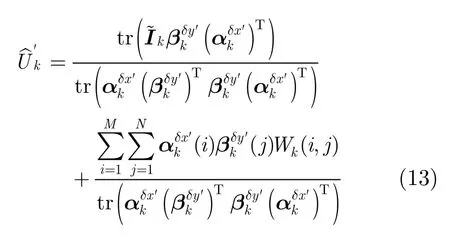
现分析噪声对散射点幅度估计的影响。式(8)重写为与前面分析类似，由李雅普诺夫中心极限定理，幅度估计的噪声同样服从高斯分布。

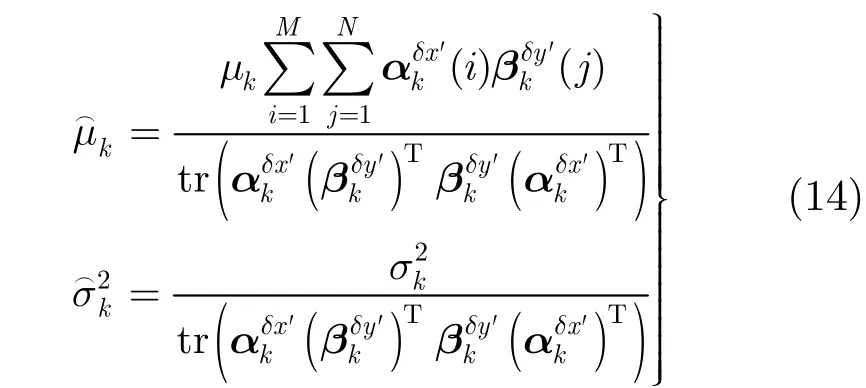
若图像噪声Wk是零均值的，对于任意一幅确定的图像，总是成立的。因此以下着重对式(12)和式(14)的方差进行分析。重写式(12)中的方差分式，并视为δx′, δy′的函数：

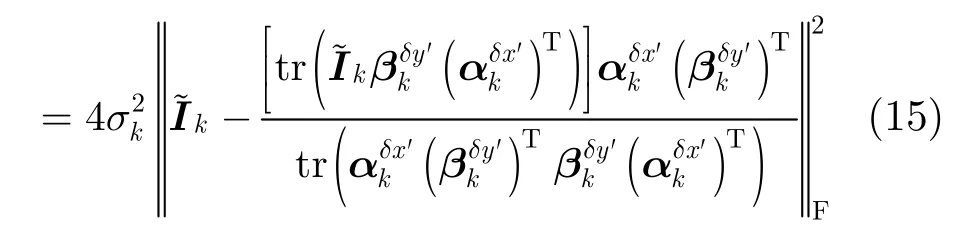
式(12)，式(14)，式(16)和式(17)相关结果显示，散射点位置参数估计时，目标函数同时受到图像噪声与重建3 dB带宽的影响，图像噪声增强与3 dB带宽的减小均会导致目标函数中噪声方差的增大；散射点幅度估计同时受到图像噪声与重建3 dB带宽的影响，图像噪声增强与3 dB带宽的减小均会导致幅度估计方差的增大。

I1为128×128像素，sinc函数中心在(65,65)，3 dB带宽为10像素，幅值为1的仿真图像。对I1加入信噪比为s的高斯白噪声，使用本文算法进行超分辨重建(200次蒙特卡洛实验)。记位置估计偏差为Δx1,Δy1，幅度估计偏差为ΔU1。图5，图6，绘制了不同信噪比下，估计误差的均值与方差随重建3 dB带宽的变化曲线。

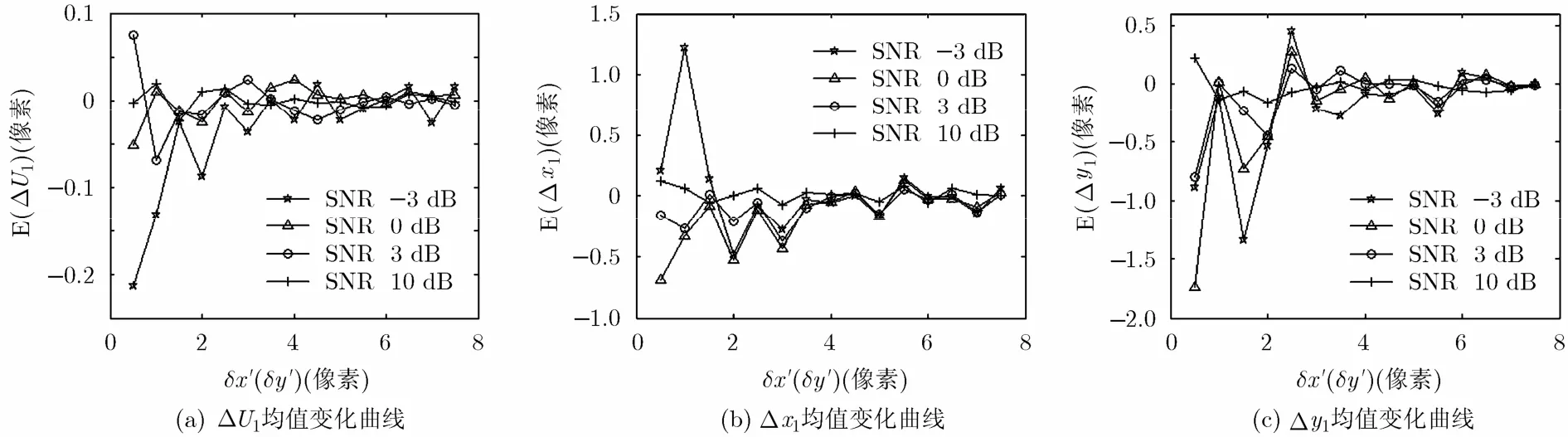
图5 不同信噪比下估计误差均值随3 dB带宽变化曲线

图6 不同信噪比下估计误差方差随3 dB带宽变化曲线

仔细分析图5，图6的仿真结果，不难发现，当重建3 dB带宽较小时，散射点参数估计的精度受信噪比影响较大，在小信噪比条件下，估计量相比无噪声情况会有较大偏差，这是因为，当3 dB带宽较小时，李雅普诺夫条件一般不满足，并且近似线性展开也存在一定的偏差。随着重建3 dB带宽的增大，散射点各参数估计接近无偏，并且信噪比的影响有逐渐减小，估计越来越稳健。因此，在高信噪比条件下，可以选择3 dB带宽更小的sinc函数以获得更高的辐射分辨率，而在低信噪比条件下，重建3 dB带宽不宜取得太小，以保证重建精度，即因为噪声的存在，重建3 dB带宽并不是越小越好，应该在重建精度和辐射分辨率之间有所权衡，一般来说可以首先估计原始图像的sinc函数3 dB带宽，然后将δx,δy设置为原3 dB带宽的1/4到1/3之间。

5 结束语

针对SAR切片ROI的超分辨问题，在稀疏框架下，提出了基于SAR成像模型与散射中心理论的超分辨重建方法。传统的雷达图像超分辨方法大部分沿用光学图像超分辨方法，本文方法从SAR成像模型出发，通过估计散射点参数，对SAR图像ROI进行超分辨重建，获得了更高的空间分辨率。该方法体现了雷达图像的自身的特征，特别适合雷达图像中的稀疏目标超分辨处理。分析了信噪比和重建3 dB带宽对参数估计精度的影响，得出了重建3 dB带宽的选择应该充分考虑重建精度与辐射分辨率的结论，给出了较为合适的重建带宽选取范围，具有一定的实际指导性。

[1] Sun J, Xu Z, and Shum H Y. Image super-resolution using gradient profile prior[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, USA, 2008: 1–8.

[2] Villena S, Vega M, Molina R, et al.. Bayesian super-resolution image reconstruction using an l1prior[C]. Proceedings of 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 2009: 152-157.

[3] Baker S and Kanade T. Limits on super-resolution and how to break them[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(9): 1167-1183.

[4] Freeman W T, Jones T R, and Pasztor E C. Example based super-resolution[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 56-65.

[5] Dong W, Zhang L, Lukac R, et al.. Sparse representation based image interpolation with nonlocal autoregressive modeling[J]. IEEE Transactions on Image Processing, 2013, 22(4): 1382-1394.

[6] Villena S, Vega M, Molina R, et al.. A general sparse image prior combination in super-resolution[C]. Proceedings of the18th International Conference on Digital Signal Processing, Fira, Greece, 2013: 1-6.

[7] Ren J, Liu J, and Guo Z. Context-aware sparse decomposition for image denoising and super-resolution[J]. IEEE Transactions on Image Processing, 2013, 22(4): 1456-1469.

[8] Pan Z, Yu J, Huang H, et al.. Super-resolution based on compressive sensing and structural self-similarity for remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(9): 4864-4876.

[9] Yang J, Wang Z, Lin Z, et al.. Coupled dictionary training for image super-resolution[J]. IEEE Transactions on Image Processing, 2012, 21(8): 3467-3477.

[10] Yang J, Wright J, Huang T S, et al.. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2851-2873.

[11] Rauhut H, Schnass K, and Vandergheynst P. Compressed sensing and redundant dictionaries [J]. IEEE Transactions on Information Theory, 2008, 54(5): 2210-2219.

[12] Aharon M, Elad M, and Bruckstein A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[13] Cetin M and Karl W C. Feature-enhanced synthetic aperture radar image formation based on non-quadratic regularization[J]. IEEE Transactions on Image Processing, 2001, 10(4): 623-631.

[14] Zhu X X and Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247-258.

[15] 张静克, 计科峰, 邢相薇. SAR目标属性散射中心特征提取与分析[J]. 雷达科学与技术, 2011, 9(3): 207-212. Zhang J K, Ji K F, and Xing X W. Feature extraction and analysis of attributed scattering centers on SAR targets[J]. Radar Science and Technology, 2011, 9(3): 207-212.

[16] Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation[M]. Norwood: MA, Artech House, 2005: 225-238.

[17] 朱磊, 水鹏朗, 武爱景. 一种SAR图像相干斑噪声抑制新算法[J]. 西安电子科技大学学报, 2012, 39(2): 80-85. Zhu L, Shui P L, and Wu A J. New algorithm for reducing speckle noise in the SAR image[J]. Journal of Xidian University, 2012, 39(2): 80-85.

[18] Tropp J A. Just relax: convex programming methods for subset selection and sparse approximation[J]. IEEE Transactions on Information Theory, 2006, 52(3): 1030-1051. [19] Li J and Stoica P. Efficient mixed-spectrum estimation with applications to target feature extraction[J]. IEEE Transactions on Signal Processing, 1996, 44(2): 281-295.

[20] Bertsekas D P and Tsitsiklis J N. Introduction to Probability [M]. Beijing: Post & Telecom Press, 2002: 379-399.

曲长文：男，1963年生，教授，博士生导师，主要研究方向为SAR系统技术、SAR信号处理、无源定位跟踪技术.

徐舟：男，1990年生，硕士生，研究方向为SAR图像解译、SAR超分辨技术.

陈天乐：男，1990年生，助理工程师，主要研究方向为新体制雷达对抗技术.

Super-resolution Reconstruction of SAR Section Based on Scattering Center Estimation and Sparse Constraint

Qu Chang-wen①Xu Zhou①Chen Tian-le②①(Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)
②(The Navy Representative Office of Nanjing 924 Factory, Nanjing 211100, China)

From the SAR imaging model, combining the scattering center theory, this paper estimates scattering centers of high resolution image from the low resolution image under the conditions of sparse. The Region Of Interesting (ROI) can be reconstructed by several sinc functions and the super resolution section is obtained after side lobe suppression. Based on the Nonlinear Least Squares (NLS) estimation, an iterative algorithm is employed to solve the super resolution reconstruction problem and the simulations are based on TerraSAR-X measurement data. Simulation results show that the proposed method is able to get higher spatial resolution and Target to Clutter Ratio (TCR) values as compared with bicubic interpolation and 1 norm regularization method. The analysis results show that the accuracy of the algorithm is affected by both the Signal to Noise Ratio (SNR) and the rebuilding 3 dB bandwidth of sinc function, the higher 3 dB bandwidth tends to be more robust to noise.

SAR; Super resolution reconstruction; Sparse representation; Nonlinear Least Squares (NLS) estimation; Robust

TP751.1

1009-5896(2015)01-0071-07

10.11999/JEIT140121

2014-01-20收到，2014-06-09改回

国家自然科学基金(61102166)资助课题

*通信作者：徐舟 zhouzhou900521@126.com