基于稀疏贝叶斯方法的脉间捷变频ISAR成像技术研究
2015-07-05苏伍各王宏强秦玉亮刘天鹏
苏伍各王宏强 邓 彬 秦玉亮 刘天鹏
(国防科技大学空间电子信息技术研究所 长沙 410073)
基于稀疏贝叶斯方法的脉间捷变频ISAR成像技术研究
苏伍各*王宏强 邓 彬 秦玉亮 刘天鹏
(国防科技大学空间电子信息技术研究所 长沙 410073)
传统捷变频成像方法具有高旁瓣、低分辨率的缺点。鉴于捷变频ISAR回波信号的稀疏性,该文基于原始数据的2维压缩感知方案,在贝叶斯原理框架下,用稀疏贝叶斯算法 方差成分扩张压缩方法(ExCoV)实现捷变频ISAR像的重建。贝叶斯框架下的稀疏重构算法考虑了稀疏信号的先验信息以及测量过程中的加性噪声,因而能够更好地重建目标系数。作为一种新的稀疏贝叶斯算法,ExCoV不同于稀疏贝叶斯学习(SBL)算法中赋予所有的信号元素各自的方差分量参数,ExCoV方法仅仅赋予有重要意义的信号元素不同的方差分量,并拥有比SBL方法更少的参数,克服了SBL算法参数多时效性差的缺点。仿真结果表明,该方法能克服传统捷变频成像缺点,并能够实现低信噪比条件下的2维高精度成像。
ISAR;捷变频;压缩感知;稀疏贝叶斯学习算法;方差成分扩张压缩方法(ExCoV)
1 引言
ISAR(Inverse SAR)图像能够提供敌方情报,侦测敌方动态,但ISAR在侦测中常受到敌方电子干扰,有效干扰的前提是能够侦测到雷达信号的工作参数,而捷变频技术因其发射相邻脉冲的载频在一定范围内快速变化,可有效防止对方对我雷达系统载频等参数的侦测[1,2]。针对ISAR成像的高逼真假目标干扰,对雷达目标识别和导弹防御带来了极大挑战[3,4]。高逼真假目标干扰的有效实施必须先侦收到雷达的信号参数,如载频、脉宽等,而捷变频技术可在一定程度上对抗高逼真假目标干扰,目前美国先进的雷达系统,如“宙斯盾”等都具备雷达参数捷变的能力。然而当雷达采用脉间捷变频技术时,雷达成像却具有一定难度,主要体现在方位向多普勒历程随载频随机变化而随机跳动,目前国内外鲜有学者研究基于捷变频的ISAR成像方法。传统的用于 ISAR成像的大时宽频带信号,如线性调频(LFM)脉冲信号、步进频信号(SF)等,在 ISAR成像过程中,这些信号的载频必须十分稳定。对于传统的基于傅里叶变换的ISAR成像算法能够简单有效地执行,但当捷变频技术用于ISAR抗干扰中时,由于载频的随机偏移破坏了回波信号的相干性,采用传统算法得到的ISAR图像无法使所有目标强散射点进行精确聚焦,并受高旁瓣和低分辨率的影响[2]。
压缩感知(Compressive Sensing, CS)[5,6]技术已广泛应用于雷达成像中[7- 10],但这些基于 CS理论的成像方法在CS重构上采用广泛使用的基于L1惩罚项的算法[11]和贪婪算法,如 BP(Basis Pursuit), SL0(Smoothed L0 norm method)[12]等,这些算法能够精确地恢复出目标散射系数,获得较高分辨率的ISAR图像[13],但这些算法的性能受人工参数设置的影响,在实际应用中很难正确地选择,并且这些算法仅考虑了信号的稀疏信息,并没有考虑目标信号的统计信息[14]。在低信噪比条件下,当前绝大多数稀疏重构算法的性能会变得很差,而相比之下基于贝叶斯理论的稀疏恢复算法,如稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)[15],贝叶斯假设检验匹配追踪[16]仍具有良好的性能。基于SBL的稀疏恢复算法是一种数据自适应算法[17],它假设目标信号具有高斯先验,并联合信号获取模型采用贝叶斯后验概率的基本原理来重构目标信号,该算法最初由Tipping提出,并由Wipf应用于稀疏信号表示中[18]。2008年文献[19]根据 SBL基本理论提出了BCS(Bayesian Compress Sensing)方法,BCS的概率模型与SBL一致,并在Spot-SAR成像中得到成功应用[20]。文献[21]基于BCS方法提出了一种稀疏优化算法,应用于稀疏孔径的高分辨ISAR成像中并取得良好的结果。SBL最主要的缺点是高计算的复杂性和需要大量的存贮要求,对于实际情况下的大尺度数据使其应用受到了限制,并受噪声性能的影响较大。2010年,文献[22]基于SBL的优越性,提出了改进的稀疏贝叶斯方法,即基于方差成分扩张压缩(Expansion-Compression Variance, ExCoV)的稀疏贝叶斯方法。ExCoV方法概况了SBL的模型[23],并拥有比SBL方法更少的参数,它利用了稀疏信号最主要的稀疏特征,即稀疏信号中大多数的元素为0或接近于0,而只有少量的具有一定意义的非0元素,因此可将信号自然地分为有重要意义的非0元素和无关紧要的元素。不同于SBL中赋予所有的信号元素各自的方差分量参数,ExCoV方法仅仅赋予有重要意义的信号元素不同的方差分量,而对剩下的元素赋予单个相同的方差分量,这种方法提供了一个对信号模型选择的框架,在该模型下采用广义最大似然方法(Generalized Maximum-Likelihood, GML)来选择系数参数,该规则不仅评价了信号表示的紧凑性和相应估计信号和数据的拟合性的程度,并采用ExCoV方法来最大化GML目标函数[22]。ExCoV方法是一个不需要信号稀疏度和噪声水平的自适应算法,且不需用收敛准则和阈值方法来终止迭代条件,由于其概率模型的简洁性,ExCoV在大尺度数据中明显快速于SBL方法,并在低信噪比的条件下获得了优于SBL的精度。
本文旨在利用 ExCoV方法求解脉间捷变频ISAR成像问题。在CS重构中,距离向和方位向同时采用稀疏贝叶斯方法进行捷变频ISAR像重构,并考虑了含噪情况下该方法的性能。实验证明基于贝叶斯理论的 CS成像技术能够有效地应用于脉间捷变频ISAR成像中,相比较传统的复后向投影变换方法和常用的CS重构方法更能突出ISAR图像的高分辨率,更能有效地实现抗干扰的目的。
2 捷变频ISAR回波信号稀疏表示模型
2.1 捷变频ISAR回波信号分析
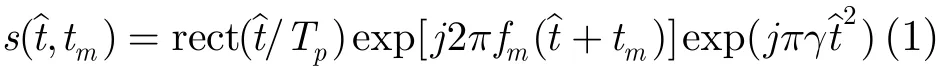
设雷达发射脉间载频捷变线性调频(FA-LFM)信号,在第m个脉冲时刻mT发射脉冲的载频为fm,线性调频信号的调频斜率为γ,脉冲宽度为Tp,脉冲重复周期为T,则第m个发射脉冲的信号形式为其中为快时间,tm=mT为慢时间。由于FA-LFM信号不同时刻的脉冲载频是不同的,且在一定的Δf范围内随机变化,其信号形式相当于对信号在频域上进行随机采样[1,2],信号采样结果为稀疏的。图1(a)和图1(b)分别给出了固定载频脉冲和随机载频脉冲的表示形式。由图1可看出两者的不同之处在于随着时间的变化它们各自的子脉冲是变化的。设雷达的成像几何模型如图2所示,其中x-o- y为目标坐标系,u- o- v为雷达坐标系,目标绕某一旋转中心转动,总转角为θm。设雷达到旋转中心的距离为R0,雷达观测角θ的变化范围为设目标的散射中心个数为N,并令为散射中心的位置。在高频处,目标总的回波可由各个散射系数的回波和来近似,当雷达发射FA-LFM脉冲信号之后,设第n个目标散射点P( x, y)在tm时刻到雷达的距离为Rn,则在tm时刻,雷达在成像场景中收到的散射点总的回波信号
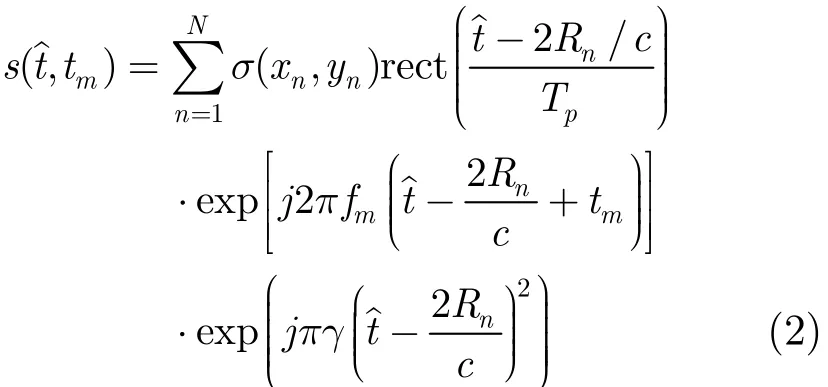
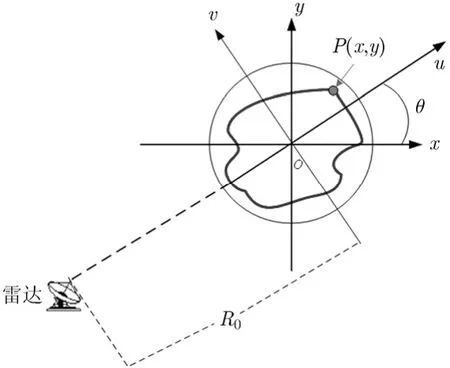
图2 ISAR成像几何模型

其中Tref为参考信号的脉宽。将式(2)与参考信号进行混频并可得差频输出为


由文献[22]中可知,式(4)中相位项第1项为距离项,第2项的相位变化使回波产生多普勒频移。对某一慢时间tm,某一固定的RΔ,在非捷变频下单个点目标在方位向上的信号小角度下是一多普勒频率为常数的信号,而在捷变频下随着载频fm的随机捷变,相位使得多普勒回波频率已不再是一常数。对于非捷变频曲线,设载频为捷变频载频的中心频率fc,其方位向的信号相位为多普勒回波频率与慢时间的关系为而捷变频回波频率与方位角度变化的关系为f( θ)=从图3中的捷变频ISAR回波相位历程曲线也可看出非捷变频的回波频率随方位角度的变化为一常数,而由于载频的随机捷变,捷变频回波频率已不再是一常数。传统的RD成像方法,要求在ISAR成像过程中载频必须十分稳定,距离向信号的脉冲压缩可采用傅里叶变换的方法实现,目标方位信号在方位向时间内多普勒频率可近似为一常数的信号,通过对时域信号在方位向进行傅里叶变换实现了信号的方位向压缩聚焦。而在捷变频ISAR回波信号中,由于载频fm的随机捷变,使得方位向多普勒频率在方位向时间内不再满足近似为常数,故采用传统的方法在方位向进行傅里叶变换,并不能实现方位向的压缩,故而不能实现所有散射点聚焦。基于捷变频ISAR回波信号的稀疏性,本文采用信号稀疏表示理论的方法来解决捷变频ISAR像聚焦问题。
2.2 捷变频ISAR回波信号稀疏表示模型
根据图2的ISAR成像几何模型,假设参考信号中的参考点为成像场景的中心,设目标的成像区域划分为K×L大小的离散区间。在目标成像场景中划分的离散点坐标值为并设该点处的散射系数大小为σk, l。设N为距离向采样点数,并设在方位向总共发射M次脉冲,则将式(5)进行低通滤波[18]之后对某一散射点回波sk, l可表示为


图3 捷变频ISAR回波相位历程

文献[7]指出当选择测量矩阵为一随机矩阵时,感知矩阵能够高概率地满足RIP条件,因此本文选取测量矩阵为随机矩阵。CS中另一核心要素为稀疏重构算法,用其来恢复出式(7)中的系数矢量σ,本文将在贝叶斯框架下求解式(7),不仅采用了稀疏先验信息,还考虑了信号统计特性,且采用稀疏贝叶斯算法无需设置人工参数,并且文献[24]指出基于L1惩罚项求得的稀疏解往往不是最稀疏的解,当真实的解是最稀疏的解时,采用SBL是更好的选择。本文采用一种改进的SBL即ExCoV方法[22]来求解式(7)。ExCoV算法能够在噪声和杂波条件下准确地估计出稀疏系数,同时能够方便地终止迭代过程,其概况了SBL的优点并优于SBL算法[22,23],本文将其结合CS理论来进行捷变频ISAR成像。
3 基于ExCoV的捷变频ISAR成像技术
根据式(7)中的雷达回波模型,设ε为0均值的高斯白噪声,方差为2δ,则s的条件概率密度函数为
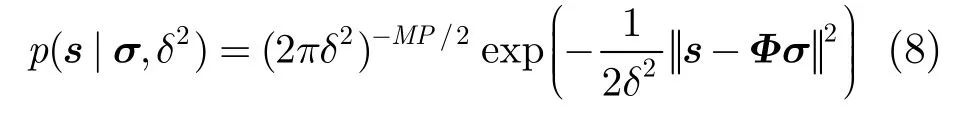
式中需要估计的矢量为目标散射系数σ和噪声方差δ2。ExCoV方法将信号σ划分为有重要意义的信号分量和相对不重要的信号分量。在ISAR成像中有意义的重要分量即为非零的目标散射系数,因此将这些信号分量赋予不同的方差分量,而对信号的其它剩余系数赋予共同的方差分量参数。定义Λ={1,2,…,Q}为信号σ分量的所有标号,这里Q=KL,记A为信号分量中赋予的不同方差分量的系数标号集,集合A为未知的,且大小qA也为未知的,并且定义补集(余集)B=ΛA为信号中相对应的拥有共同方差分量的信号系数的标号集,且有qB= Q-qA。同样对应地将词典Φ根据信号σ的标号集分为子矩阵MN,同理将信号σ对应地划分为σA∈RqA和
ExCoV方法对信号系数σ采取如式(9)的先验模型:
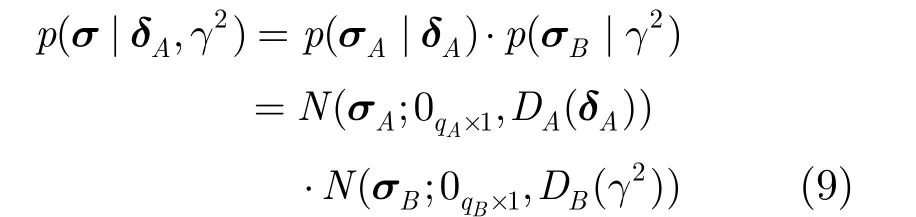

式(10)即为ExCoV方法的代价函数。对于给定的标号集A,文献[22]详细地阐述了基于贝叶斯后验概率,采用GML定理来求解参数集x。
传统的基于CS的成像方法对回波数据采用分频处理的方法[10,25],其忽略了各频点回波数据间的耦合效应,图像质量将有所损失。本文采用一种距离向和方位向回波数据同时进行降采样的采样机制,即2维数据联合处理的方式[20],假设距离向随机采样J(J<N)点,方位向获得的脉冲回波数为(J~<M),此时有效的感知矩阵降为JJ~×KL。在采样完成之后,再应用ExCoV算法进行稀疏重构,通过此采样方案能够有效地减少回波数据,图4给出了本文针对捷变频ISAR提出的一种2维CS成像的信号处理流程图。
4 仿真实验
本节通过仿真实验来验证所提出的基于ExCoV的捷变频ISAR 2维CS成像方法,雷达参数设置如表1所示,雷达发射线性调频信号,采样点数256,转动期间雷达录取的回波数为512,并在仿真中加入复高斯白噪声。捷变载频的变化范围一般不会超过中心频率的10%~20%,相邻脉冲的子载频的临界频差要远大于脉宽的倒数0.2 MHz,取到脉宽的10%。本节中设相邻载频差在1~10 MHz内随机变化,并假设雷达目标区域在10×10的范围内,设置场景中的目标位置如图5所示,将其离散化的间隔设为0.2 m,将仿真结果与传统的成像方法和常用的稀疏恢复方法进行比较。

表1 雷达仿真参数设置
4.1 传统成像方法
本节采用传统的成像算法RD算法和复后向投影变换方法[26]来进行捷变频ISAR成像,在点目标回波数据中加入了10 dB的复高斯白噪声,图6给出了两种方法实现的捷变频ISAR像。图6(a)中RD成像的方法不能使所有的散射点进行聚焦,这是由于载频的随机捷变使得回波频率与慢时间不再保持线性关系,无法实现所有的捷变频方位向聚焦。图6(b)中复后向投影变换方法能够较好地实现方位向的脉冲压缩,但是复后向投影变换方法的成像性能受带宽影响较大,这是由于它重构过程中利用的是目标的距离像信息,受sinc函数主瓣宽度的影响,带宽越小影响越大,从图中也可看出其旁瓣较高,存在虚假点目标,成像效果模糊。
4.2 2维联合CS捷变频ISAR成像方法
由于IAA(Iterative Adaptive Approach)算法也是一种无参数化的自适应稀疏恢复算法,并成功应用于SAR成像中[27],本文采用一种基于训练样本的MIAA算法[28],该算法是在传统IAA算法的基础上改进的,其计算复杂度和时效性方面要优于传统的IAA算法。为验证所提CS捷变频成像方法的有效性,并与常用的稀疏恢复算法SL0, MIAA和SBL进行比较,在对捷变频ISAR回波数据进行降采样时,距离向随机采样J=30个频点,方位向随机取脉冲回波数25。图7~图10给出了不同信噪比下基于不同稀疏恢复方法的捷变频ISAR成像结果。由实验结果可以看出,相比传统成像算法,基于CS的成像方法能够利用较少的测量数据获得具有更好聚焦质量的图像。在信噪比为-8 dB时,SL0方法、MIAA方法和SBL方法获得的雷达图像中有大量的杂波,目标基本被淹没,但是ExCoV方法获得的捷变频ISAR图像仍能准确地估计出目标散射点的位置,获得最为清晰的ISAR像。随着SNR的增加,SL0方法、MIAA方法和SBL方法获得ISAR像杂波逐渐减少,但仍有较强的噪声干扰,综合比较可看出,基于ExCoV的方法性能明显优于其它稀疏恢复算法,对噪声具有较强的稳健性。

图4 捷变频ISAR的CS 2维成像信号处理流程
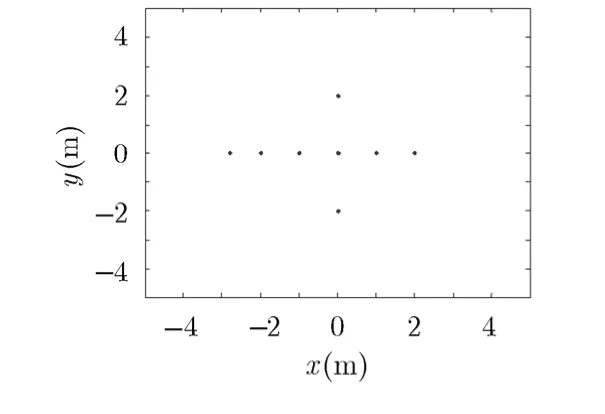
图5 ISAR目标模型空间结构分布

图6 传统方法的捷变频ISAR成像结果

图7 SNR为-8 dB时获得的捷变频ISAR像

图8 SNR为-4 dB时获得的捷变频ISAR像

图9 SNR为1 dB时获得的捷变频ISAR像
为验证本文方法捷变频ISAR像的重建性能,设置蒙特卡洛次数为100,图11(a)给出了各稀疏恢复算法获得的均方差(Mean Squared Error, MSE) 随SNR变化的曲线图。在此MSE定义为MSE=其中为真实点目标的散射系数,σ为估计的目标散射点系数。图11(b)给出了在同样的情况下各稀疏恢复算法运行时间的情况。从图11(a)中综合比较可以看出,在低噪声情况下,ExCoV方法拥有最低的MSE,具有较好的抗噪性能,从中也可看出,当SNR小于-10 dB时,ExCoV方法得到的MSE大于1,此时得到的捷变频ISAR像将可能引起模糊。在运行时间上,ExCoV方法也拥有最快的速度,SBL方法具有最大的时耗性,此特点也是SBL方法最大的缺点。本文采用的基于训练样本的MIAA算法,具有比传统IAA算法较高的精度,因而总体性能要优于SBL。综上可知在一定的成像条件下,综合考虑ISAR成像的质量和成像的实时性,基于ExCoV的捷变频ISAR成像方法是较好的成像方法。
在以上实验中,传统成像方法采用了全部的回波数据,稀疏表示方法仅采用了部分回波数据,综合比较不难看出,即使是在信噪比较高时,基于稀疏表示方法获得的捷变频ISAR像结果均优于传统成像结果,因而基于稀疏表示的捷变频ISAR成像方法是可行的。鉴于当前SBL在稀疏恢复算法中的优越性及存在的缺点,ExCoV在SBL的模型选择及参数估计上进行了改进,仿真实验表明其捷变频ISAR成像无论在抗噪性能上,还是在成像效果上均优于其它常用的稀疏恢复算法。
5 结束语

图10 SNR为6 dB时获得的捷变频ISAR像

图11 不同SNR条件下各方法成像性能比较
基于贝叶斯理论的稀疏恢复算法是当前研究CS恢复算法的一个热点。ExCoV算法性能受人工参数设置影响低,当在稀疏表示问题中真实的解是最稀疏的解时,采用ExCoV算法往往能够达到最真实的稀疏解。本文针对传统成像算法应用于脉间捷变频ISAR成像中,因其存在的多普勒调频率捷变带来的高旁瓣和低分辨率的问题,并考虑到其回波信号的稀疏性,首次将基于ExCoV的2维CS理论应用于捷变频ISAR成像中,达到抗有源欺骗干扰的目的,并在低信噪比的情况下用仿真实验证明了该方案的可行性。未来的工作将继续探索、开发快速的基于贝叶斯理论的稀疏恢复算法及在一定的信噪比条件下,研究其成像效果,并考虑采用实测数据验证该方案的成像效果。
[1] Richard G W. 吕跃广, 译. 电子情报 雷达信号截获与分析[M]. 北京: 电子工业出版社, 2008: 12-18. Richard G W and Lu Yue-guang. translation. Elint The Interception and Analysis of Radar Signals[M]. Beijing: Publishing House of Electronics Industry, 2008: 12-18.
[2] 赵宗峰. 基于信号波形设计的SAR抗干扰技术研究[D]. [硕士论文], 国防科技大学, 2007. Zhao Zong-feng. SAR anti-jamming based on waveform design[D]. [Master dissertation], National University of Defense Technology, 2007.
[3] 赵博, 周峰, 保铮. 基于电磁散射模型的ISAR空中目标欺骗干扰方法[J]. 电子与信息学报, 2014, 36(1): 194-201. Zhao Bo, Zhou Feng, and Bao Zheng. Deception jamming for ISAR aerial target based on electromagnetic scattering model[J]. Journal of Electronics & Information Technology, 2014, 36(1): 194-201.
[4] Pan Xiao-yi, Wang Wei, Feng De-jun, et al.. On deception jamming for countering bistatic ISAR based on sub-Nyquist sampling[J]. IET Radar, Sonar & Navigation, 2014, 8(3): 173-179.
[5] Candès E, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[6] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[7] Yang Jun-gang, Thompson J, Huang Xiao-tao, et al.. Random-frequency SAR imaging based on compressed sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 983-994.
[8] Ugur S and Arikan O. SAR image reconstruction and autofocus by compressed sensing[J]. Digital Signal Processing, 2012, 22(7): 923-932.
[9] Rao Wei, Li Gang, Wang Xi-qin, et al.. Adaptive sparse recovery by parametric weighted L1minimization for ISAR imaging of uniformly rotating targets[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 942-952.
[10] 刘天鹏, 刘振, 魏玺章. 基于压缩感知的脉间捷变频SAR成像研究[J]. 电子学报, 2012, 40(6): 1073-1078. Liu Tian-peng, Liu Zhen, and Wei Xi-zhang. Research on interpulse frequency agility SAR imaging via compressed sensing[J]. Acta Electronica Sinica, 2012, 40(6): 1073-1078.
[11] Samadi S, Çetin M, and Ali M. Multiple feature-enhanced SAR imaging using sparsity in combined dictionaries[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 821-825.
[12] Hosein M G, Babaie Z M, and Jutten C. A fast approach forovercomplete sparse decomposition based on smoothed l0norm[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 289-301.
[13] Liu Zhen, You Peng, Wei Xi-zhang, et al.. Dynamic ISAR imaging of maneuvering targets based on sequential SL0[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1041-1045.
[14] Xu Gang, Xing Meng-dao, Zhang Lei, et al.. Bayesian inverse synthetic aperture radar imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1150-1154.
[15] Zhang Zhi-ling and Rao B. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912-926.
[16] 甘伟, 许录平, 苏哲, 等. 基于贝叶斯假设检验的压缩感知重构[J]. 电子与信息学报, 2011, 33(11): 2640-2646. Gan Wei, Xu Lu-ping, Su Zhe, et al.. Bayesian hypothesis testing based recovery for compressed sensing[J]. Journal of Electronics & Information Technology, 2011, 33(11): 2640-2646.
[17] Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 2(1): 211-244.
[18] Wipf D P and Rao B D. Sparse Bayesian learning for basis selection[J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153-2164.
[19] Ji S, Xue Y, and Carin L, Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356.
[20] 徐建平, 皮亦鸣, 曹宗杰. 基于贝叶斯压缩感知的合成孔径雷达高分辨成像[J]. 电子与信息学报, 2011, 33(12): 2863-2868. Xu Jian-ping, Pi Yi-ming, and Cao Zong-jie. SAR imaging based on Bayesian compressive sensing[J]. Journal of Electronics & Information Technology, 2011, 33(12): 2863-2868.
[21] Zhang Lei, Qiao Zhi-Jun, Xing Meng-dao, et al.. Highresolution ISAR imaging by exploiting sparse apertures[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2): 997-1008.
[22] Qiu K and Aleksandar D. Variance-component based sparse signal reconstruction and model selection[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 2935-2952.
[23] Aleksandar D and Qiu K. ExCoV: expansion-compression variance-component based sparse-signal reconstruction from noisy measurements[C]. Proceeding of 43rd Annual Conference Information Science and Systems, Baltimore, USA, 2009: 186-191.
[24] Wipf D and Nagarajan S. Iterative reweighted l1and l2methods for finding sparse solutions[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 317-329.
[25] Alonso M T, Paco L D, and Jordi J M. A novel strategy for radar imaging based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4285-4295.
[26] Ash J N. An autofocus method for backprojection imagery in synthetic aperture radar[J]. IEEE Geoscience Remote Sensing Letters, 2012, 9(1): 104-108.
[27] Glentis G O, Zhao K X, Jakobsson A, et al.. Non-parametric high-resolution SAR imaging[J]. IEEE Transactions on Signal Processing, 2013, 61(7): 1614-1624.
[28] Yang Zhao-cheng, Li Xiang, Wang Hong-qiang, et al.. Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J]. Signal Processing, 2013, 93(12): 3567-3577.
苏伍各: 男,1986年生,博士生,研究方向为雷达成像技术及稀疏表示方法.
王宏强: 男,1970年生,研究员,博士生导师,研究方向为雷达信号处理、压缩感知、太赫兹雷达技术等.
邓 彬: 男,1981年生,讲师,研究方向为合成孔径雷达、太赫兹雷达.
秦玉亮: 男,1980年生,副研究员,研究方向为雷达信号处理.
刘天鹏: 男,1985年生,副研究员,研究方向为雷达成像、雷达对抗与交叉眼干扰技术.
The Interpulse Frequency Agility ISAR Imaging Technology Based on Sparse Bayesian Method
Su Wu-ge Wang Hong-qiang Deng Bin Qin Yu-liang Liu Tian-peng
(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Traditional frequency agility ISAR imaging method suffers from high sidelobe and low resolution. To improve the resolution, by exploiting the sparsity of targets in the
echo, this paper uses the sparse Bayesian algorithm, namely Expansion-Compression Variance-component based method (ExCoV), to reconstruct the ISAR image from the original Compressed Sensing (CS) ISAR data. By taking into account of the prior information of the sparse signal and the additive noise encountered in the measurement process, the sparse recover algorithm under the Bayesian framework can reconstruct the scatter coefficient better than the traditional methods. Different from the Sparse Bayesian Learning (SBL) endowing variance-components to all elements, the ExCoV only endows variance-components to the significant signal elements. This leads to much less parameters and faster implementation of the ExCoV than the SBL. The simulation results indicate that it can conquer the problem brought by traditional methods and achieve high precision agility ISAR imaging under the low SNR.
ISAR; Frequency agility; Comressed Sensing (CS); Sparse Bayesian Learning (SBL) algorithm; Expansion-Compression Variance (ExCoV) component
TN957.52
A
1009-5896(2015)01-0001-08
10.11999/JEIT140315
2014-03-10收到,2014-09-02改回
国家自然科学基金(61171133)和国家自然科学青年基金(61101182, 61302148)资助课题
*通信作者:苏伍各 suwuge_zhanlang@sina.com
