空间色噪声背景下双基地多输入多输出雷达低仰角估计方法

洪 升 万显荣柯亨玉

(武汉大学电子信息学院 武汉 430072)

空间色噪声背景下双基地多输入多输出雷达低仰角估计方法

洪 升 万显荣*柯亨玉

(武汉大学电子信息学院 武汉 430072)

针对多径效应的影响，该文提出一种空间色噪声背景下双基地多输入多输出(MIMO)雷达低仰角估计方法。首先对双基地MIMO雷达中低仰角目标的多径环境进行建模，同时考虑发射和接收端的镜面反射信号，并用空间色噪声模拟漫反射。然后利用协方差矩阵求差方法消除未知色噪声的影响，在发射端和接收端进行空间平滑对多径信号解相干，即进行空间差分平滑处理。最后利用酉变换旋转不变技术(ESPRIT)算法估计目标的发射角(DOD)和接收角(DOA)。该文指出特殊情况下空间差分平滑协方差矩阵缺秩的问题，并提出一种修正的空间差分平滑方法。该算法对阵元数要求不高，适用于未知噪声背景及低信噪比环境，并且解决DOD与DOA联合估计的角度兼并问题。仿真实验表明了所提算法的有效性。

双基地MIMO雷达；发射角；接收角；空间色噪声；低仰角估计

1 引言

多输入多输出MIMO雷达是一种新体制雷达。相对于传统的相控阵雷达体制，MIMO雷达拥有更多的自由度，可以克服衰落效应，改善空间分辨率，增强参数识别能力和提高目标侦测性能。MIMO雷达可分为分布式MIMO雷达和紧凑式MIMO雷达。分布式MIMO雷达[1]各阵元在地域上广泛分布；紧凑式MIMO雷达[2]各收发阵元布置紧凑。本文讨论紧凑式双基地MIMO雷达中的低仰角估计问题。

低仰角跟踪一直是雷达面临的难题。由于低空目标的直达波与地面的多径反射波在同一波束宽度内叠加，低仰角目标检测和参数估计困难。近年来常规相控阵雷达的低仰角估计问题得到了充分的研究[3- 6]，且很多双基地MIMO雷达的发射角(Direction of Departure, DOD)和接受角(Directionof Arrival, DOA)联合估计算法也被提出 。然而，针对收发多径环境下MIMO雷达特别是双基地MIMO雷达低仰角估计问题的讨论相对较少。文献[12]提出一种基于波束空间的角度估计算法。文献[13]通过构造一个前后向矩阵束，完成了单基地MIMO雷达低仰角的快速估计。

本文建立了双基地MIMO雷达中低空目标的多径模型。考虑发射端和接收端的镜面反射，电磁波从发射天线到接收天线共有4条相干路径。同时考虑地面垂直向的漫反射杂波，将噪声建模为空间相关的平稳高斯噪声。针对高斯空间色噪声环境，文献[14]在发射端对三阵元的匹配滤波器输出进行互相关以消除高斯空间色噪声的影响。文献[15]提出了基于四阶累积量的MUSIC-ESPRIT算法。为了完成目标的低仰角估计，需要对相干多径解相干。文献[16]提出一种双基地MIMO雷达色噪声背景下的相干源角度估计方法，该方法借鉴了文献[14]中去色噪声的思想，利用发射分集平滑的方法进行解相干，采用DOA矩阵法进行角度估计。然而该方法在具有相同DOD或相同DOA角度时是失效的，即出现了类似DOA矩阵法中的角度兼并问题[17]。本文算法借鉴文献[18]中的协方差矩阵求差方法去除背景色噪声的影响；同时为解决角度兼并的问题，在发射端和接收端进行空间平滑。仿真证明本文方法在所建的多径模型下可以成功地估计低空目标的仰角。

本文符号说明：Jm代表m×m维的交换矩阵(反对角线为1，其他元素为0), In× n或In表示n×n维的单位矩阵，0m× n代表m×n维的零矩阵。⊗表示Kronecker乘积。

2 信号模型

考虑一个窄带双基地MIMO雷达系统，发射阵列为垂直维的M元均匀线阵，接收阵列为垂直维的N元均匀线阵。远场低空有一点目标，电磁波的多径传播模型如图1所示。由于地面的反射，在发射端有发射直射和发射反射两条路径到达目标。发射端反射系数为ρt，发射直射角为θd，发射反射角为θi。在接收端，同样存在接收直射和接收反射两条路径到达接收阵列。接收端反射系数为ρr，接收直射角为φd，接收反射角为φi。接收的信号矢量为

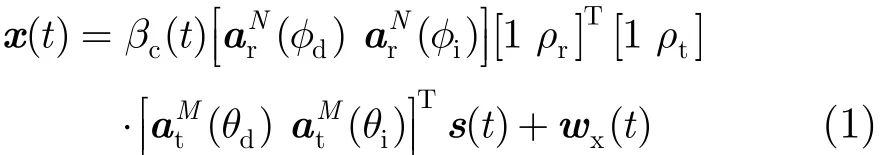
图1 双基地MIMO雷达多径反射模型

对Y(l)进行行向量化，利用Kronecker乘积的性质，有

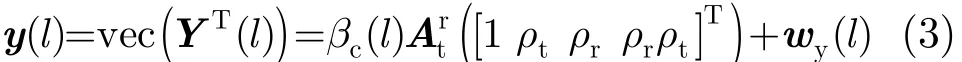
3 MIMO雷达中空间色噪声下相干源角度估计

3.1 MIMO雷达中的分集平滑

双基地MIMO雷达中低仰角目标的角度估计类似于色噪声下相干信号的2维角度估计。2维角度估计的ESPRIT算法、矩阵束算法以及DOA矩阵法在角度兼并的情况下容易失效[17]。在本文的建模下，等效的4个相干目标存在严重的角度兼并(即存在相同的DOD和相同的DOA)。此时MIMO雷达中常用的发射分集平滑和接收分集平滑解相干能力失效，文献[16]的方法失效。此处以发射分集平滑为例进行简单说明。

3.2 MIMO雷达中的空间差分平滑

类似地，有

命题1 在本文构建的信号模型中，如果m0≥P+1, n0≥P+1, 且pt≥P/2, pr≥P/2，则当P为偶数时，rank(ΔRf)=P ；当P为奇数时，rank(ΔRf)=P-1。

证明 将式(9)和式(10)代入式(8)有

显然，ΔRf=-JMN(ΔRf)*JMN，即ΔRf为一负反对称矩阵。如果(λi, ui)为ΔRf的一对特征值和特征矢量，则也为ΔRf的特征值及特征矢量。由式(11)知ΔRf的特征值为实数。当P为奇数时，必然有一对特征值满足λi=-λi*且λi为实数，于是λi=0。所以ΔRf的秩只能为偶数。根据文献[21]中的讨论可知当P为偶数时，rank(ΔRf)=P ；当P为奇数时，rank(ΔRf)=P-1。 证毕

ΔRf包含了对的前向和后向空间平滑信息，使得P条多径下的低仰角估计只需(3/2)P个发射和接收阵元，降低了对天线阵元数的要求。由上述证明过程知，造成ΔRf缺秩的本质原因为ΔRf的负反对称结构。为保证ΔRf的满秩，需破坏ΔRf的负反对称结构。类似于文献[18]中的改进措施，定义修正的空间差分平滑矩阵为

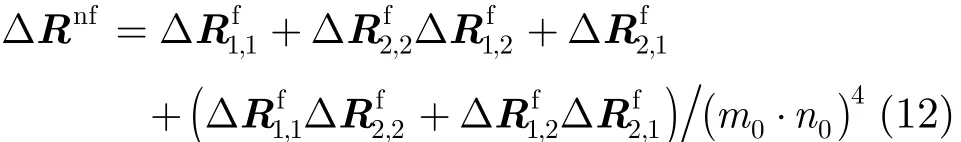
3.3 酉变换ESPRIT

经过空间差分平滑处理后，可采用酉变换ESPRIT方法[8]在实数域估计DOA和DOD。酉变换ESPRIT需要中心埃尔米特(Hermitian)对称的协阵的正定性。由于所用快拍数有限，构造准确的中心埃尔米特(Hermitian)对称协方差矩阵(常规空间差分平滑方法)时当的处理相当对可用快拍进行了加倍，能改善算法的测角性能。通过酉变换可将复数矩阵变换为实数矩阵采用文献[8]的方法，基于总体最小二乘(Total Least Square, TLS)准则实现实数域DOD与DOA的联合估计。

4 算法仿真和性能分析

实验1 采用本文所提方法和文献[16]中的方法分别对低空目标1进行DOD和DOA估计。假设发射接收直达波信号的信噪比(SNR)为30 dB，进行100次Monte Carlo仿真。图2为常规空间差分平滑方法并用酉变换ESPRIT进行角度估计的结果；图3为文献[16]方法进行角度估计的结果。可知，在本文建立的多径模型下，即存在角度兼并时，文献[16]方法是失效的，本文方法能够更为稳健地估计低空目标的仰角。

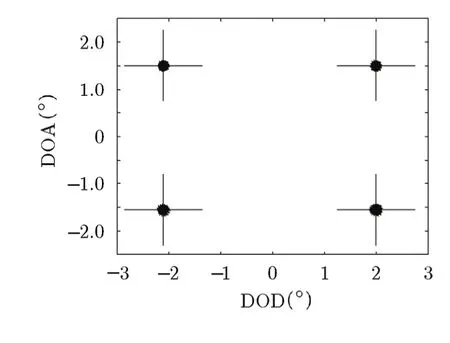
图2 本文方法的角度估计结果

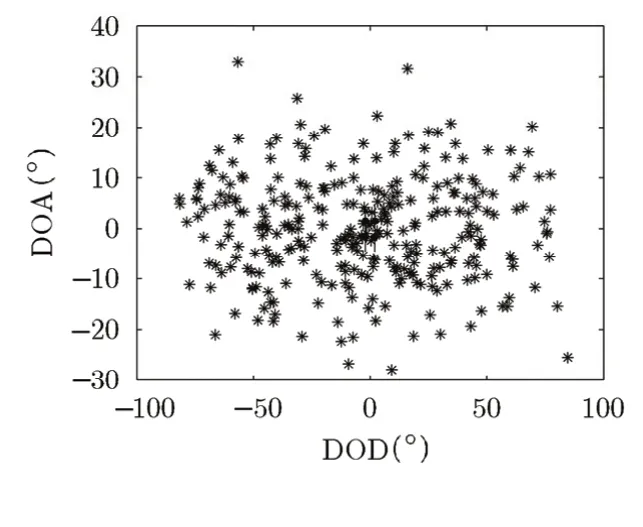
图3 文献[16]方法的角度估计结果

实验2 采用本文算法在不同信噪比下分别对低空目标1和低空目标2独立进行DOD和DOA估计，验证算法的有效性，分析算法的测角性能。对于低空目标，发射端直射波和反射波的角度间隔以及接收端直射波和反射波的角度间隔都很小，如果测角误差较大，便不能将直达波和反射波区分开来，仰角的估计失去意义。因此定义一个界限误差角如果角度估计的绝对误差超过χ，便认为角度估计失败。统计100次仿真中角度估计成功的仿真次数，求出DOA和DOD估计的成功概率如图4所示，此成功概率即算法对目标的分辨概率，体现了算法的分辨能力。图4中rCD_SS代表实数域(酉变换ESPRIT)的常规空间差分平滑方法；cCD_SS代表复数域(直接ESPRIT)的常规空间差分平滑方法；rMCD_SS代表实数域的修正空间差分平滑方法；cMCD_SS代表复数域的修正空间差分平滑方法。由图4可知角度估计的成功概率存在一个SNR门限，超过这个SNR门限才可以以100%的概率将目标多径的直达波和反射波分开。修正的空间差分平滑算法的SNR门限明显低于常规的空间差分平滑算法，而且酉变换ESPRIT算法的分辨能力要略优于直接ESPRIT算法。由于目标2的位置高于目标1，分辨目标2多径的SNR门限比分辨目标1的门限低。仿真表明所提算法在低信噪比下即能获得较优的角度分辨能力。

图4 4条多径下目标1和目标2的角度估计分辨概率

图5 4条多径下不同方法对目标1的角度估计结果

图5给出了4种方法对目标1多径进行100次Monte Carlo仿真的DOA和DOD估计结果，SNR 为30 dB。由图可知，本文算法对DOA和DOD的估计是无偏估计，修正的空间差分平滑方法的估计性能优于常规的空间差分平滑方法。图6为用4种方法进行角度估计的均方根误差(Root Mean Square Error, RMSE)随SNR的变化曲线。对比4种方法的估计结果，可知复数域ESPRIT算法和实数域ESPRIT算法的估计精度差不多，但后者可极大程度地减小计算量。相对于常规的空间差分平滑方法，修正的空间差分平滑方法能够提高测角分辨率，改善测角精度。由仿真结果可知，基于酉变换ESPRIT的修正空间差分平滑算法是较优的选择。

实验3 本实验假设目标1和目标2的第4条多径信号很微弱，淹没在噪声中。这时算法需要分辨的是对应着的3条多径信号。图7给出了4种方法的分辨概率。此时常规空间差分平滑方法失效，估计的成功概率为0。图8 为4种方法对目标1多径进行100次Monte Carlo估计的结果，SNR 为30 dB。由图可知常规空间差分平滑方法的估计结果是随机的且不收敛于准确值的，而修正空间差分平滑方法的估计仍能收敛于准确值。图9为DOD和DOA估计的均方根误差曲线。对比实验2发现，由于多径信号减少，算法的分辨性能和估计精度都得到了提高。

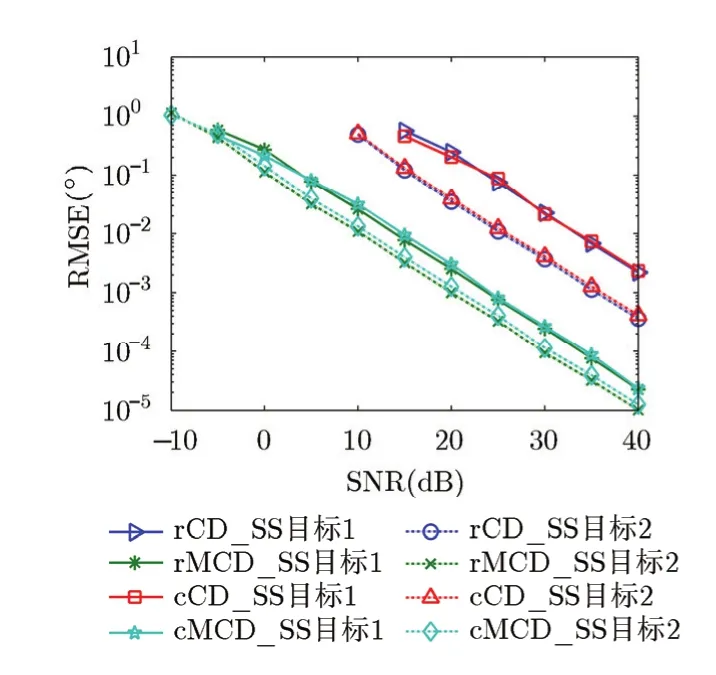
图6 4条多径下目标1和目标2的角度估计均方根误差

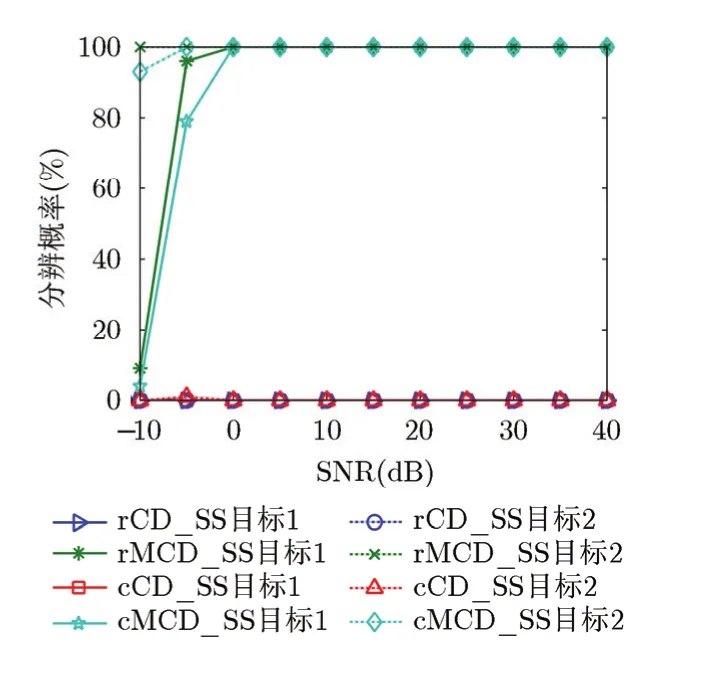
图7 3条多径下目标1和目标2的角度估计分辨概率

图8 3条多径下不同方法对目标1的角度估计结果

实验4 本实验在没有角度兼并的情况下，比较修正空间差分平滑方法和文献[16]中方法的测角性能。首先假设有4个相干目标，其DOD依次为DOA依次为15°]， 其他仿真条件和前述一致，角度估计的RMSE曲线如图10所示。由于文献[16]中方法的原理为基于发射分集平滑的互相关矩阵分解，图中标注为TDS_Croscorr。去掉第4个目标，对剩下的3个目标进行估计，仿真结果如图11所示。由图可知在没有角度兼并的情况下，本文所提的修正空间差分平滑方法优于文献[16]中方法。实际上，此时多目标的角度间隔远大于低仰角估计中的角度间隔，算法能在较低的信噪比下获得较高的估计精度。

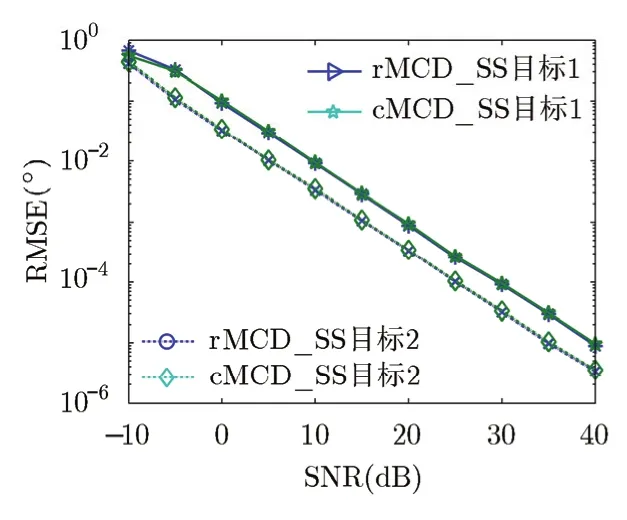
图9 3条多径下目标1和目标2的角度估计均方根误差

图10 4个相干目标的角 度估计均方根误差

图11 3个相干目标的角 度估计均方根误差

5 结束语

本文针对空间色噪声中双基地 MIMO雷达低仰角目标的角度估计问题，提出空间差分平滑算法和修正的空间差分平滑算法。该算法利用差分矩阵法消除时间平稳噪声的影响，降低了对信噪比的要求，广泛适用于空间色噪声和空间白噪声的情况。为解决DOD和DOA联合估计的角度兼并问题，本文对发射阵列和接收阵列分别进行空间平滑。同时文中也指出了在奇数条多径的情况下，常规空间差分平滑方法失效。为此提出一种修正的空间差分平滑方法。仿真实验验证分析了常规空间差分平滑和修正空间差分平滑方法的性能。通过比较发现，修正空间差分平滑方法有更好的稳健性和估计性能。

[1] Haimovich A M, Blum R S, and Cimini L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116-129.

[2] Li J and Stoica P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[3] 刘俊, 刘峥, 刘韵佛. 米波雷达仰角和多径衰减系数联合估计算法[J]. 电子与信息学报, 2011, 33(1): 33-37. Liu Jun, Liu Zheng, and Liu Yun-fo. Elevation angle and multipath fading coefficient joint estimation algorithm in VHF radar[J]. Journal of Electronics & Information Technology, 2011, 33(1): 33-37.

[4] Zhu Wei and Chen Bai-xiao. Altitude measurement based on terrain matching in VHF array radar[J]. Circuits, Systems, and Signal Processing, 2013, 32(2): 647-662.

[5] 陈根华, 陈伯孝, 朱伟. 干涉阵列米波雷达的低仰角高精度估计方法[J]. 西安电子科技大学学报(自然科学版), 2012, 39(6): 42-48. Chen Gen-hua, Chen Bai-xiao, and Zhu Wei. High accuracy estimation of low elevation angle based on interferometric array in VHF radar[J]. Journal of Xidian University (Nature Science Edition), 2012, 39(6): 42-48.

[6] Zhao Ying-jun, Wang Yong-liang, Li Rong-feng, et al.. Angle measurement for meter-wave radar based on mainlobe multipath jamming suppression[C]. IEEE 11th International Conference on Signal Processing (ICSP), Beijing, China, 2012: 1746-1750.

[7] Wang Wei, Wang Xian-peng, Li Xin, et al.. DOA estimation for monostatic MIMO radar based on unitary root-MUSIC[J]. International Journal of Electronics, 2013, 100(11): 1499-1509.

[8] Zheng Gui-mei, Chen Bai-xiao, and Yang Ming-lei. Unitary ESPRIT algorithm for bistatic MIMO radar[J]. Electronic Letters, 2012, 48(3): 164-165.

[9] Wang Wei, Wang Xian-peng, Ma Yue-hua, et al.. Conjugate unitary ESPRIT algorithm for bistatic MIMO radar[J]. IEICE Transactions on Electronics, 2013, E96-C(1): 124-126.

[10] 陈金立, 李家强, 顾红. 双基地 MIMO 雷达高速运动目标的DOD 和 DOA 联合估计[J]. 电子与信息学报, 2013, 35(4): 859-864. Chen Jin-li, Li Jia-qiang, and Gu Hong. Joint DOD and DOA estimation of high speed moving target in bistatic MIMO radar[J]. Journal of Electronics & Information Technology, 2013, 35(4): 859-864.

[11] 许凌云, 张小飞, 许宗泽, 等. 双基地MIMO雷达四维角度和多普勒频率联合估计[J]. 电子与信息学报, 2012, 34(12): 2942-2947. Xu Ling-yun, Zhang Xiao-fei, Xu Zong-ze, et al.. Joint 4-D angle and doppler frequency estimation for bistatic MIMO radar[J]. Journal of Electronics & Information Technology, 2012, 34(12): 2942-2947.

[12] 刘俊, 刘铮, 谢荣, 等. 基于波束空间的米波MIMO雷达角度估计算法[J]. 电子学报, 2011, 39(9): 1962-1966. Liu Jun, Liu Zheng, Xie Rong, et al.. Beam-space domain angle estimation algorithm in VHF MIMO radar[J]. Acta Electronic Sinica, 2011, 39(9): 1962-1966.

[13] 谢荣, 刘铮, 刘俊. 基于矩阵束的 MIMO雷达低仰角快速估计方法[J]. 电子与信息学报, 2011, 33(8): 1833-1838. Xie Rong, Liu Zheng, and Liu Jun. Fast algorithm for low elevation estimation based on matrix pencil in MIMO radar[J]. Journal of Electronics & Information Technology, 2011, 33(8): 1833-1838.

[14] Jin Ming, Liao Gui-sheng, and Li Jun. Joint DOD and DOA estimation for bistatic MIMO radar[J]. Signal Processing,2009, 89(2): 244-251.

[15] 刘晓莉, 廖桂生. 基于MUSIC 和ESPRIT 的双基地MIMO雷达角度估计算法[J]. 电子与信息学报, 2010, 32(9): 2179-2183. Liu Xiao-li and Liao Gui-sheng. Combined MUSIC with ESPRIT algorithm for angle estimation in bistatic MIMO radar system[J]. Journal of Electronics & Information Technology, 2010, 32(9): 2179-2183.

[16] 符渭波, 苏涛, 赵永波, 等. 双基地MIMO雷达相干源角度估计方法[J]. 西安电子科技大学学报(自然科学版) , 2012, 39(2): 120-126. Fu Wei-bo, Su Tao, Zhao Yong-bo, et al.. Method for angle estimation of coherent sources in bistatic MIMO radar[J]. Journal of Xidian University (Nature Science Edition), 2012, 39(2): 120-126.

[17] 金梁，殷勤业. 时空DOA矩阵方法[J]. 电子学报, 2000, 28(6): 8-12. Jin Liang and Yin Qin-ye. Space-time DOA matrix method[J]. Acta Electronica Sinica, 2000, 28(6): 8-12.

[18] 齐崇英, 王永良, 张永顺, 等. 色噪声背景下相干源DOA 估计的空间差分平滑算法[J]. 电子学报, 2005, 33(7): 1314-1318. Qi Chong-ying, Wang Yong-liang, Zhang Yong-shun, et al.. Spatial difference smoothing algorithm for DOA estimation of coherent sources in the presence of colored noise fields[J]. Acta Electronic Sinica, 2005, 33(7): 1314-1318.

[19] Boman K and Stoica P. Low angle estimation: models, methods, and bounds[J]. Digital Signal Processing, 2001, 11(1): 35-79.

[20] Chen Yih-min. On spatial smoothing for two-dimensional direction of arrival estimation of coherent signals[J]. IEEE Transactions on Signal Processing, 1997, 45(7): 1689-1696.

[21] Choi Y H. Subspace-based coherent source localisation with forward/backward covariance matrices[J]. IEE Proceedings-Radar Sonar and Navigation, 2002, 149(3): 145-151.

洪 升： 女，1987年生，博士生，研究方向为阵列信号处理、MIMO雷达信号处理等.

万显荣： 男, 1975年生，教授，博士生导师，研究兴趣包括：超视距雷达和无源雷达系统、雷达信号处理等.

Low-elevation Estimation for Bistatic MIMO Radar in Spatially Colored Noise

Hong Sheng Wan Xian-rong Ke Heng-yu
(School of Electronic Information, Wuhan University, Wuhan 430072, China)

Concerned with the influence of multipath, this paper proposes a spatially differencing smoothing technique for the low-elevation estimation in the bistatic MIMO radar under the spatially colored noise. Firstly, the multipath environment for a low-elevation target in the bistatic MIMO radar is modeled, by considering the specular reflection of the transmitter and receiver. The diffuse reflection is assumed to be the spatially colored noise. Then, the covariance matrix differencing is used to eliminate the unknown noise component, and the transmitting array and receiving array are spatially smoothed to decorrelate the multipath signals, which does the spatially differencing smoothing operation. Finally, the Direction of Departures (DODs) and Direction of Arrivals (DOAs) are estimated by unitary Estimation of Signal Parameters using Rotational Invariance Techniques (ESPRIT) algorithm. This paper also points to the rank deficiency problem of the spatially differencing smoothed covariance matrix in a special case, and modifies the spatially differencing smoothing method correspondingly. The proposed methods require a small number of antenna elements, fit for general unknown noise fields and low SNR environment, and solve the angle-merging problem in joint DOD and DOA estimation. The simulation results demonstrate the effectiveness of the proposed method.

Bistatic MIMO radar; Direction of Departure (DOD); Direction of Arrival (DOA); Spatially colored noise; Low elevation estimation

TN958

A

1009-5896(2015)01-0015-07

10.11999/JEIT140290

2014-03-05收到，2014-07-28改回

国家自然科学基金(61331012, 61371197, U1333106, 61271400)和教育部博士点基金(20120141110077)资助课题

*通信作者：万显荣 xrwan@whu.edu.cn