在初中数学课堂中进行启发式教学初探
2015-07-02彭洪
彭洪
【关键词】启发式教学 数学课堂 认知结构
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2015)06A-0081-01
开展启发式教学是数学课堂中的重要措施,对提升学生的积极性和主动性有重要意义,能够培养学生的创新精神和独立性。在课堂教学中,教师要充分结合学生的知识发展水平,以自身经验为基础,进行启发式教育,采取有效的措施引导学生独立思考,进行探究式学习,并通过彼此交流,促进学生思维的提升和数学能力的改善。
一、启发学生自己从实践中得出数学结论
从学生的角度出发,学习内容和数学知识等都是未知的,对于学生而言,数学学习是发现的过程,是探索知识的过程。由于知识水平和认知程度限制,初中生对教材的认知程度有限,无法完成教材中众多的结论性知识的独立学习。因此,教师应该以典型材料为基础,让学生充分认识材料的基础上进行抽象概括,并对数学结论进行总结。
例如在教学人教版七年级数学上册《有理数的加法》时,如果在教学过程中直接将加减法的准则告诉学生,并让学生进行计算,效果不突出,不能引发学生思考,对学生充分掌握知识技能不利。如果教师充分结合实际案例,让学生在故事背景中学习有理数的加减法,能显著提升学习效果。教学时教师可以采用以下方式让学生进行问题思考:
1.上半场赢3个球,下半场赢5个球,则全场比赛结果是 个球。
2.上半场输4个球,下半场输2个球,则全场比赛结果是 个球。
3.上半场赢3个球,下半场输4个球,则全场比赛结果是 个球。
4.上半场赢6个球,下半场输2个球,则全场比赛结果是 个球。
5.上半场输5个球,下半场赢5个球,则全场比赛结果是 个球。
6.上半场输2个球,下半场不输不赢,则全场比赛结果是 个球。
学生回答上述问题,并经过思考后将赢球的个数记为正,输球的个数记为负,给学生留下深刻的印象,有利于学生绝对数学式的解答。根据上述表达,学生列出对应的表达式进行计算,然后对表达式进行分析和观察,对掌握有理数加减法法则具有重要意义。
利用球赛的具体案例进行分析,不仅提升了学生的积极性,同时案例生动形象,学生很容易列出表达式。这个启发过程中,学生掌握了数学理论,掌握了应用知识和技能,数学能力得到了提升。
二、启发学生从多角度分析问题
数学思想方法是提升学生认知的灵魂。如何在数学教学中引导学生学习数学思想方法呢?首先应该进行启发式教学,在教学过程中不断提升学生的参与热情,通过适当的方式启发学生从多角度分析问题,提升学生思维的独立性和发现问题、解决问题的能力。教师在教学过程中应以数学知识的形成过程为基础,促进数学教学方法和数学思维在知识学习中的利用。
例如,在人教版七年级数学下册中,关于多边形有这样一个结论:“多边形的外角和是360°。”并且以六边形为例进行了分析研究。教学时,教师可以采取多种措施,从多个角度引导学生分析问题,提升学生的认识程度。
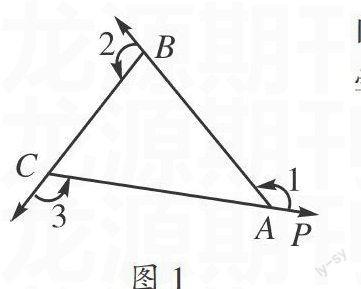
首先,借助图1,对上述问题进行分析:从图中的A点位置出发,在AP方向上出现了第一次转角,用∠1表示,视线方向用AB表示,然后沿着视线方向向B点走,并且出现了第二次转角,用∠2表示,视线方向为BC,同样沿着BC的方向向C点走,出现第三次转角,用∠3表示,视线方向用CA表示,并且沿着视线方向向A点出发,回到了原来的位置。通过上述分析,经过三次转角后,回到了原来的位置,由此可知,三个角度旋转了360°,即三角形的外角和是360°。最后,使用同样的方法对n边形的n个外角和进行思考,得出同上结论。
此外,还可以引导学生对多边形的定义进行学习,并且利用内角和外角的关系进行问题的解决。
∵多边形的外角是与它有公共顶点的内角的邻补角,
∴n边形的内角和+n边形的外角和=n·180°.
又∵n边形的内角和=(n-2)·180°,
∴n边形的外角和=n·180°-(n-2)·180°=360°.
综上所述,形象直观是第一种方法的典型特征,体现了具体思维的作用,联系性强,技巧性高。而第二种方法则充分利用了多种知识之间的联系性,并以认知结构为基础,将新知识融入,但是整体直观性较差,对学生的要求较高,需要有较强的知识基础,并具备逻辑推理能力。这两种方法各有优缺点,但总体而言对提升学生的思维能力有着重要意义,对知识的形成有强调作用。
总之,在数学教学中,教师应充分发挥启发式教学的重要作用,充分发挥数学学科的特征,以启发式教学为基础,促进内在规律的掌握,引导教学实践,提升教学层次。
(责编 林 剑)
