放射性成因同位素地球化学参数的误差计算:以Hf-Nd-Sr同位素为例
2015-07-02吴宇宸杨岳衡杨进辉
吴宇宸, 杨岳衡, 杨进辉
(1. 北京大学 数学科学学院, 北京 100871; 2. 中国科学院 地质与地球物理研究所, 北京 100029)
0 引 言
同位素地球化学是地球科学的重要分支学科,目前在地球的形成与演化、地质作用的进程与机理等方面的研究中发挥着越来越重要的作用[1]。可以说, 同位素地球化学已成为解决地球科学重大问题不可或缺的重要工具[2]。同位素地球化学包括放射性成因同位素和稳定同位素地球化学两个主要方面,其中放射性成因同位素地球化学的核心是利用放射性衰变基本原理和母-子体的质量关系, 确定若干同位素地球化学参数, 然后根据这些参数来对地球的地球化学储库和地质作用过程等进行定量刻画。很显然, 这些地球化学参数数值的大小及性质对我们来说至关重要。同等重要的是这些参数的误差, 因为它决定了这些参数的可信范围。一般说来, 基于同位素比值的这些地球化学参数涵义各不相同, 甚至涉及复杂的数学运算。显然, 这些参数误差的确定需要一定, 甚至专门的数学知识。
本文从误差的基本概念出发, 介绍误差运算的基本方法, 然后介绍Sr-Nd-Hf同位素体系中代表性地球化学参数的误差计算实例, 并附有简洁明了的Excel计算表格, 供读者使用。由于笔者数学基础知识有限, 欢迎读者批评指正。
1 误差的基本概念及物理意义
在介绍误差的运算法则之前, 我们需要先明确各种误差的数学定义以及它们的物理意义。误差(Error)是一个较为宽泛的概念, 它与我们经常用到的偏差(Deviation)这一概念易于混淆, 但实际上它们的物理意义完全不同。误差指的是某一测量量的测量值与真值的差别, 而偏差指的是该测量量与参考值的偏离程度。在这一基础上, 与本文密切相关的概念有方差、标准差、标准偏差和标准误差等, 以下逐一介绍。有希望全面了解误差理论的读者, 请参阅相关文献[3]。
1.1 方差(Variance)
根据数理统计的基本原理, 对某一直接测量量进行多次测量所得到的数据应该服从正态分布N(μ,σ2)。式中μ为真值, σ2为方差。但请注意的是,这两个参数量均为理论值, 我们实际上永远无法知道它们的确切值。
虽然我们不可能知道上述两个量的确切值, 但在实际工作中可对它们进行大概的估计。在实际情况下, 当我们对这个测量量测量一组数据, 并计为X1,… , Xn时, 则m的估计值是上述测量值的算术平均值, σ2的估计值为这是因为根据数理统计的结果[4],是σ2的无偏估计, 即这个估计不包含系统误差。因此, 我们也可将定义成一组数据的方差, 是表示一组数据中各个数据分别与其平均数之差的平方的平均数的统计量。
1.2 标准偏差与标准差(Standard Deviation, 简称SD)
标准偏差(Standard Deviation)简称标准差(SD), 就是方差的开平方, 又称均方差, 即从该式可知, 该参数表示的是一组数据对其算术平均值的偏离或离散程度, 是数据精密度的衡量指标。标准差小, 仅表示该组测量值密集分布在平均值附近, 与数据的准确性并无联系。
1.3 标准误差(Standard Error, 简称SE)
方差和标准差这两个统计量只能描述测量结果的离散程度。对于一个不精确的测量方法而言, 测量充分多次后, 总能得到可靠的结果, 但数据的方差基本不变。因此, 方差本身实际上无法反映这组测量结果的准确性。或者说, 用同一种测量方法对某一测量量分别进行 100次和 10000次测量, 一定是后者所得到的平均值更可靠, 误差更小, 但它们的方差和标准差差别不大, 无法反映上述两组测量情形下的误差大小。而下面介绍的标准误差这个统计量较好地克服了这一问题, 并且对原数据的信息保存比较好, 故现在的测量误差多指标准误差。
一组数据的标准误差实质上是根据这组数据所得到的测量量的估计值(这里为平均数)与真值之差的大小的统计量。它的计算公式为这个公式的严格证明涉及比较复杂的测度论知识,现简述如下。当测出数据为 X1,… ,Xn时, 其真值 θ后验分布为其中此结论的数学证明尽管复杂, 但从直观上不难想象它是正确的。对上式 化 简, 可 以 得 到 分 布 为 ξ ( θ| X1,… ,Xn)=这正是正态分布的表达式。因此, 我们可以将数据的平均值作为真值的估计量, 而即为此估计的标准差。而σ可以用估计, 因此这组数据的标准误差可以用来估计。
标准误差反映估计值和真值之差的大小, 而且当测量无穷多次时, 标准误差趋近 0, 所以标准误差可以很好地测定由一组数据所确定的估计值的误差。
在实际应用中, 某测量量的测量结果可表示为X = A±a, 这里的A为真值的估计值, a就是A的标准误差, 也就是我们一般情形下理解的误差。a既可以是一个具体数值, 此时称a为绝对误差; a也可以是一个比例(如 2%), 这样就是相对误差。换算成绝对误差即为X = A±Aa。
由于绝对误差便于从数学上计算, 所以本文一律采用绝对误差。
在地球化学实际运用过程中, 其测定量的误差来自多个方面, 既包括测量误差, 也包括系统误差,本文对此不做区分和讨论。但需要指出的是, 标准偏差与标准误差这两个概念在应用中经常被混淆[5]。实际上, 标准偏差(SD)反映的是一组测量值对平均值的分散程度, 与误差实际上毫无关系。如我们通常在实际测定过程中需要测定某一同位素标准的比值,并给出其标准偏差, 实际上这就是反映本次测量的精密或离散程度。而标准误差(SE)是测量平均值与真值之差的大小。对一未知的测量量而言, 测量次数越多, 获得的平均值与真值就越接近, 即标准误差就越小。当然, 标准误差也不是测量值的实际误差或误差范围, 它只是对一组数据可靠性的估计。标准误差小, 测量的可靠性大。反之, 测量就不大可靠。
2 误差的合成与传递
为便于读者理解, 我们首先介绍两个有误差的量的和及标准误差的计算公式。设: X = A±α, Y = B±β, 则这 是 因 为X~所 以X + Y ~ N( A + B,即
下面介绍标准误差传递公式。
若f = f(X1,… ,Xn), X1的标准误差为 σi, 且相互独立, 而且 f满足一定条件(这样的条件初等函数都能满足), 则 f的标准误差 σ的表达式为
下面粗略证明上式。由于是误差运算, 所以可以认为对每个iX, 它们与真值相差不多, 因此 f在误差范 围 内 可 近 似 写 成X其中i为此变量的真值。
然后, 关于标准误差, 以下3条自然成立:
(1) 常数的标准误差为0;
(2) 变量放大或缩小多少倍, 则标准误差放大、缩小多少倍;
(3) 两个变量之和的标准误差的平方等于两个变量的标准误差平方和。
由此为常数, 标准误差为 0。的标准误差即为的标准误差, 即为
公式中的每个称为该变量的误差传递系数。
根据上述原理, 简单测量量的误差数学运算可概括如下:

但对于复杂的测量量误差计算, 我们仍需要对所有影响误差的测量量求偏导, 然后根据求出的各个偏导数, 计算出此即为最后的标准误差。
3 同位素地球化学中若干重要参数的误差计算
同位素是指质子数(原子序数)相同、而中子数不同的同一元素。例如, O (氧)有3个同位素, 即16O、17O和18O, 它们的质子数均为 8, 但中子数分别为8、9和10。质子数和中子数相加即为质量数, 也就是同位素的质量。
同位素有多重分类。根据它们在形成后是否会衰变成其他元素可将同位素划分为稳定同位素和放射性同位素。所谓稳定同位素, 它在形成后一直保持不变, 如现今广泛应用的C (12C、13C、14C)、H (1H、2H、3H)、O (16O、17O、18O)、S (32S、33S、34S、36S)、Li (6Li、7Li)、Mg (24Mg、25Mg、26Mg)、Fe (54Fe、56Fe、57Fe)等; 而放射性同位素则在形成后发生衰变成为新的同位素。如,87Rb通过衰变形成87Sr,而 Sr有 4个同位素, 分别为84Sr、86Sr、87Sr和88Sr。
在放射性同位素领域, 目前常用的地球化学体系有 Lu-Hf、Sm-Nd、Rb-Sr、Re-Os、U-Pb 等, 其中尤以前 3组体系应用最为广泛[1]。因此, 本文将着重讨论这3组同位素体系中关键参数的误差计算问题。
3.1 Hf同位素参数误差计算
Hf同位素体系中较为重要的参数有:

式中: s = 样品; λ = 1.867 × 10–11a–1[7]; CHUR = 球粒陨石; DM = 亏损地幔。球粒陨石和亏损地幔的Lu-Hf同位素参数为[8–9]:
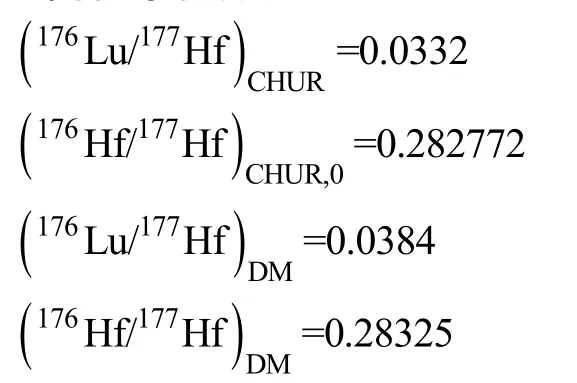
上述这些参数的具体物理意义可参见图 1。εHf(0)实际上就是样品的176Hf/177Hf比值与现今球粒陨石的对比情况, 而 εHf(t)是指样品形成时其176Hf/177Hf比值与当时球粒陨石的对比情况。tDM1是样品 εHf(0)和 t时 εHf(t)两点连线与亏损地幔的交点(连线斜率与 fs相关), 又称Hf同位素单阶段模式年龄, 其公式推导可参阅文献[1,10]。但在部分情况下,样品模式年龄的计算涉及两阶段模式, 又称Hf同位素两阶段模式年龄(tDM2)。此时, 第 1阶段直线的斜率与平均大陆地壳一致(fcc= –0.55, 即大陆地壳的176Lu/177Hf = 0.015[11], 而第2阶段直线的斜率与tDM1时相同。
3.1.1 εHf(0)误差的计算
根据公式× 1 0000, 这里 (176H f/177Hf)CHUR,0为常数, 所以这个量由一个直接测量量完全确定, 标准误差为
3.1.2 εHf(t)误差的计算
根据公式这里 (176H f/177Hf)CHUR,0,是常数。εHf(t)这个量由 3个测量量(176Hf/177Hf、176Lu/177Hf和 t)共同决定, 而且关系比较复杂, 最终的标准误差也比较复杂, 公式为:

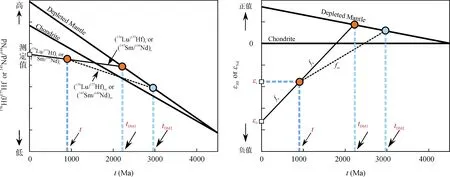
图1 Hf (Nd)同位素地球化学参数图示Fig.1 Schematic Hf or Nd isotopic parameters
此公式由于要对各测量量求偏导, 故计算式相当复杂。但是, 根据文献[10], εHf(t)与 t近似呈线性关系。此时, 上述公式可简化为:
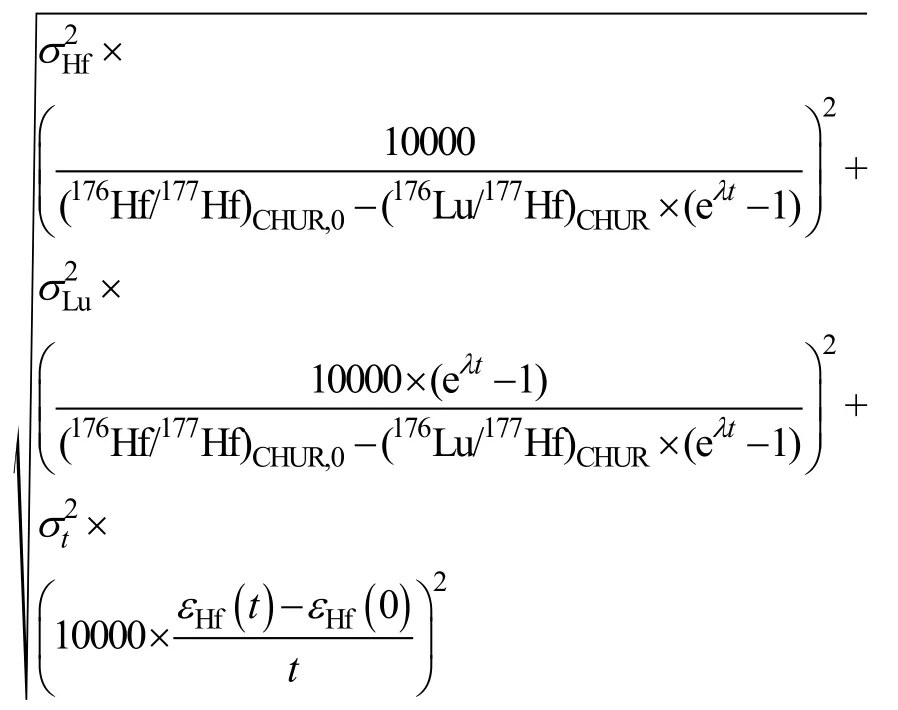
实际演算发现, 此式与前面精确式的计算结果相差不大。
3.1.3 tDM1误差的计算
根据公式这个参数由两个测量量(176Hf/177Hf和176Lu/177Hf)完全决定, 其标准误差为
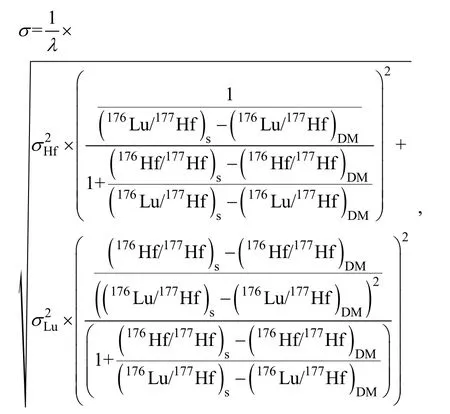
此式也较为复杂, 但可以化简为
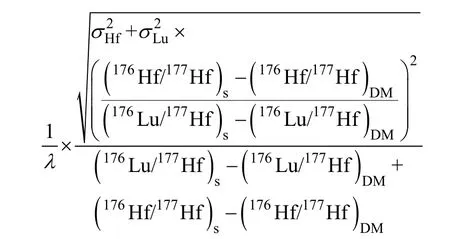
3.1.4 tDM2误差的计算
根据公式由于tDM1的标准误差完全由σH2f与σL2u决定, 与t独立, 因此可以相加。经过移项, 可得: tDM2=
其标准误差为
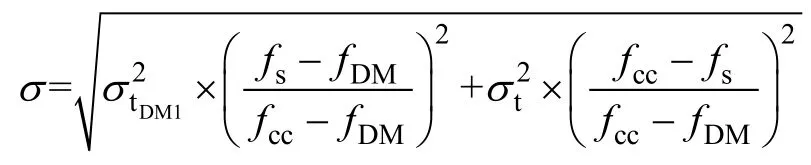
式中: σtDM1为tDM1的标准误差。
但值得指出的是, 上述式中并没有考虑 fs的误差。如果考虑, 则误差可以写成
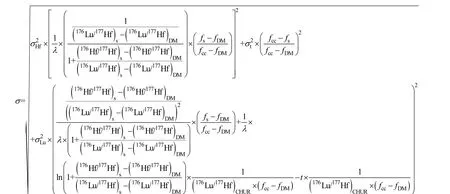
3.1.5 fs误差的计算
根据公式这里为常数, 所以这个量由一个直接测量量(176Lu/177Hf)完全确定, 标准误差为
3.2 Nd同位素参数误差计算
与Hf同位素类似, 涉及Nd同位素的主要参数有εNd(0)、εNd(t)、tDM1和 tDM2。它们的计算方法与Hf同位素完全相同, 所以其标准误差的公式也与其类似。所不同的是147Sm的衰变常数[12], 及相关的球粒陨石和亏损地幔的参数[1]。
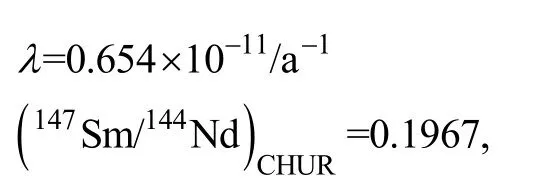
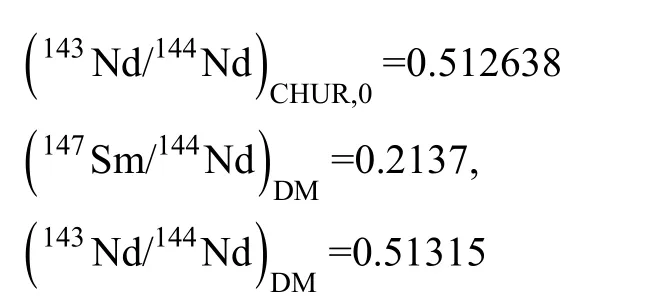
3.3 Sr同位素参数误差计算
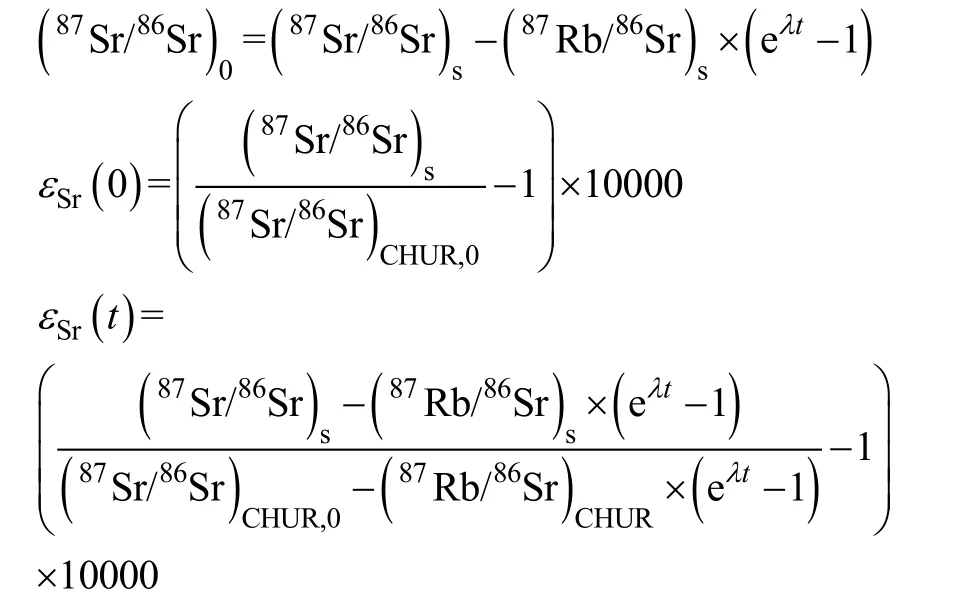
Sr同位素地球化学参数相对较少, 主要参数的表达式如下:式中: s = 样品; λ = 1.42×10–11a–1[13]; CHUR = 球粒陨石; (87Rb/86Sr)CHUR= 0.0827; (87Sr/86Sr)CHUR,0=0.7045[1]。
这样的标准误差计算公式是:
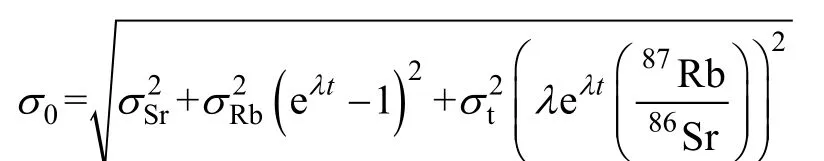
而εSr(0)和εSr(t)的误差计算与Hf-Nd同位素原理相同, 此处不再赘述。与Hf、Nd同位素不同的是, 我们很少用Sr同位素数据来计算模式年龄。
3.4 地球化学储库参数变化情形下的误差计算
在上述各参数的误差计算过程中, 我们假设所采用的衰变常数、球粒陨石与亏损地幔的同位素组成均为常量(表 1), 但实际情况并非如此。以 Hf同位素为例, Blichert-Toft et al.提出球粒陨石的176Lu/177Hf和176Hf/177Hf比 值 为 0.0332±2 和0.282772±29[8], 但 Patchett et al.却发现上述两值存在较大的变化范围[14], 并给出其平均值分别为0.0342和0.282843。Bouvier et al.通过更细致的工作提出球粒陨石的176Lu/177Hf和176Hf/177Hf比值为0.0336±1和 0.282785±11[15], 其中176Lu/177Hf比值较Blichert-Toft et al.提出的高约1%左右,176Hf/177Hf比值高出约0.5ε单位。近来, Iizuka et al.提出球粒陨石的上述比值为0.0338±1和0.282793±11[16], 显示这方面的研究目前正处于进展之中。从图2的结果可以看出,球粒陨石参数的变化对样品εHf(t)误差的影响显著存在。由于这些参数的具体数据目前并无定论, 因而我们在此很难评估它对相关参数的影响程度。但我们建议, 当读者在进行具体样品的计算时, 应首先注明所采用的参数值, 以利于不同研究之间的对比。

表1 Hf-Nd-Sr同位素计算中的主要地球化学常量Table 1 Major geochemical constants as userd for Hf-Nd-Sr isotopic calculations
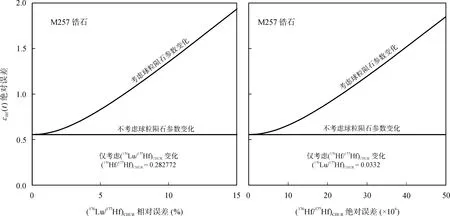
图2 球粒陨石参数变化情形下M257标准锆石εHf(t)的误差Fig.2 εHf(t) errors of zircon M257 when the parameters of referenced chondrite vary
4 结 论
(1) 大多数同位素地球化学参量都是非直接测量量, 它们误差的计算涉及到复杂程度不等的数学的运算。如 εHf(0)标准误差的计算相对简单, 但εHf(t)标准误差的计算则要复杂得多。不过, 如果能对参量的表达式做一些合理的近似, 那么其标准误差的计算会简单很多;
(2) 尽管部分参数标准误差的计算相对复杂,但它们的计算并非不可实现。为方便读者, 本文提供了简洁实用的Excel表格, 供读者使用。李献华、李秋立研究员曾就误差的基本概念和计算与作者进行了深入讨论; 两位评审人对本文提出的宝贵修改意见使得本文的质量得到很大提高,在此一并致以衷心的感谢。
:
[1] Faure G, Mensing T M. Isotopes: Principles and Applications [M].3rd ed. New Jersey: John Wiley, 2005: 1–897.
[2] Dickin A P. Radiogenic Isotope Geology [M]. 2nd ed. Cambridge: Cambridge University Press, 2005: 1–492.
[3] 吴石林, 玘张. 误差分析与数据处理[M]. 北京: 清华大学出版社, 2010: 1–255.Wu Shi-lin, Zhang Qi. Error Analysis and Data Processing [M].Beijing: Tsinghua University Press, 2010: 1–255 (in Chinese).
[4] 陈家鼎, 孙山泽, 李东风, 刘力平. 数理统计学讲义[M].第二版. 北京: 高等教育出版社, 2006: 361–368.Chen Jia-ding, Sun Shan-ze, Li Dong-feng, Liu Li-ping.Mathematical Statistics Teaching Materials [M]. 2nd ed. Beijing: Higher Education Press, 2006: 361–368 (in Chinese).
[5] 郝拉娣, 于化东. 标准差与标准误[J]. 编辑学报, 2005,17(2): 116–118.Hao La-di, Yu Hua-dong. Standard deviation and standard error of arithmetric mean [J]. Acta Edit, 2005, 17(2): 116–118(in Chinese with English abstract).
[6] 何书元. 概率论[M]. 北京: 北京大学出版社, 2006: 95–142.He Shu-yuan. Probability Theory [M]. Beijing: Peking University Press, 2006: 95–142 (in Chinese).Scherer E, Munker C, Mezger K. Calibration of the lutetium-hafnium clock [J]. Science, 2001, 293(5530): 683–687.
[7] Scherer E, Munker C, Mezger K. Calibration of the lutetiumhafnium clock [J]. Science, 2001, 293(5530): 683–687.
[8] Blichert-Toft J, Albarede F. The Lu-Hf isotope geochemistry of chondrites and the evolution of the mantle-crust system [J].Earth Planet Sci Lett, 1997, 148(1/2): 243–258.
[9] Griffin W L, Pearson N J, Belousova E, Jackson S E, van Achterbergh E, O’Reilly S Y, Shee S R. The Hf isotope composition of cratonic mantle: LAM-MC-ICPMS analysis of zircon megacrysts in kimberlites [J]. Geochim Cosmochim Acta, 2000, 64(1): 133–147.
[10] DePaolo D J. Neodymium Isotope Geochemistry: An Introduction [M]. Berlin: Spring-Verlag, 1988: 1–187.
[11] Griffin W L, Wang X, Jackson S E, Pearson S E, O’Reilly S Y,Xu X S, Zhou X M. Zircon chemistry and magma genesis, SE China: In-situ analysis of Hf isotopes, Tonglu and Pingtan igneous complexes [J]. Lithos, 2002, 61(3/4): 237–269.
[12] Begemann F, Ludwig K R, Lugmair G W, Min K, Nyquist L E,Patchett P J, Renne P R, Shih C Y, Villa I M, Walker R J. Call for an improved set of decay constants for geochronological use [J]. Geochim Cosmochim Acta, 2001, 65(1): 111–121.
[13] Steiger R H, Jäger E. Subcommission on Geochronology:Convention on the use of decay constants in geo- and cosmochronology [J]. Earth Planet Sci Lett, 1977, 36(3): 359–362.
[14] Patchett P J, Vervoort J D, Soderlund U, Salters V J M. Lu-Hf and Sm-Nd isotopic systematics in chondrites and their constraints on the Lu-Hf properties of the Earth [J]. Earth Planet Sci Lett, 2004, 222(1): 29–41.
[15] Bouvier A, Vervoort J D, Patchett P J. The Lu-Hf and Sm-Nd isotopic composition of CHUR: Constraints from unequilibrated chondrites and implications for the bulk composition of terrestrial planets [J]. Earth Planet Sci Lett, 2008, 273(1/2): 48–57.
[16] Iizuka T, Yamaguchi T, Hibiya Y, Amelin Y. Meteorite zircon constraints on the bulk Lu-Hf isotope composition and early differentiation of the Earth [J]. Proc Nat Am Soc, 2015,112(17): 5331–5336.
