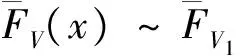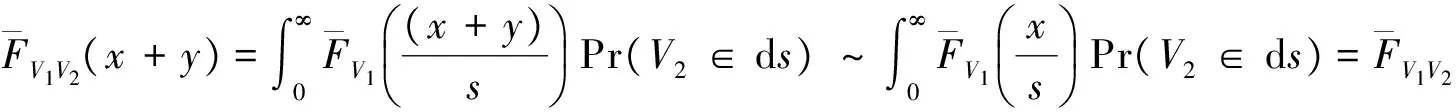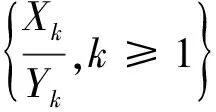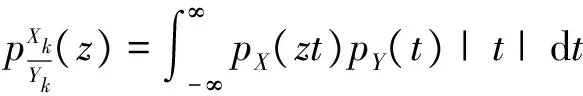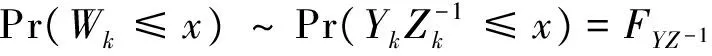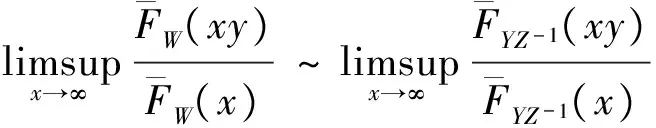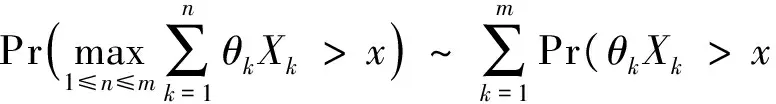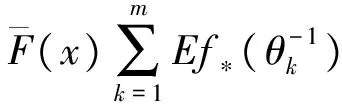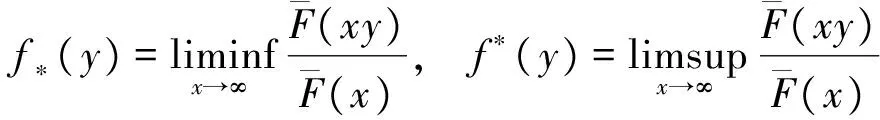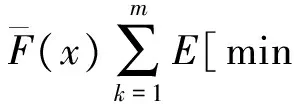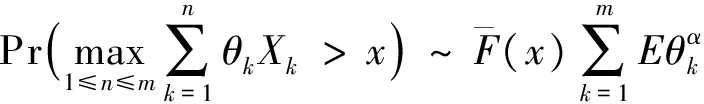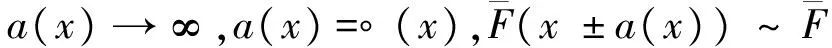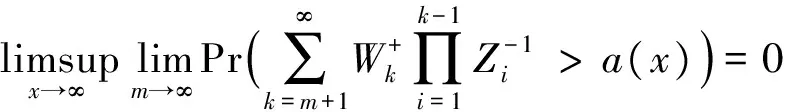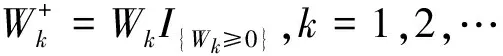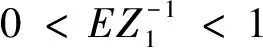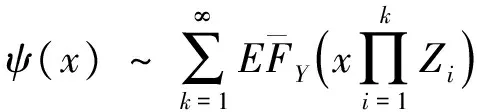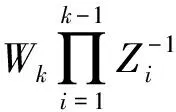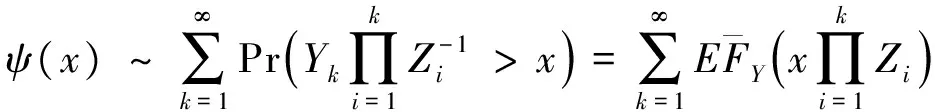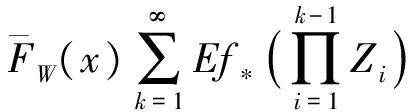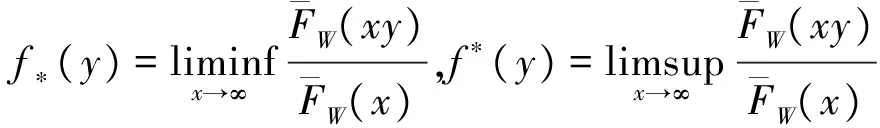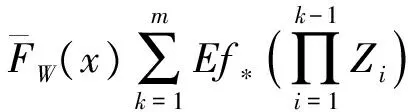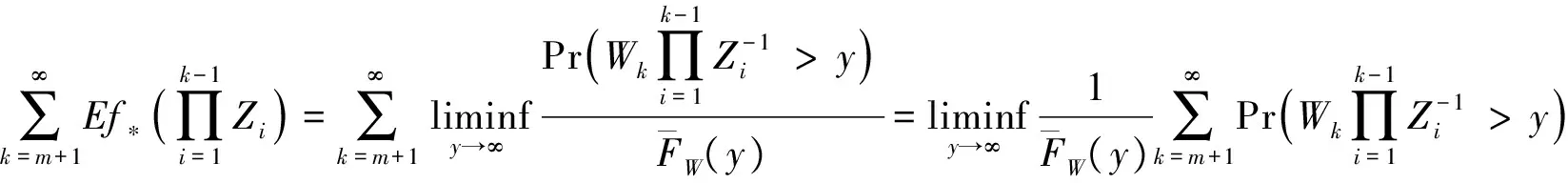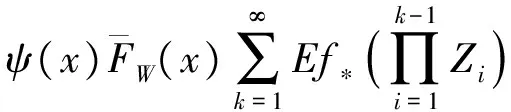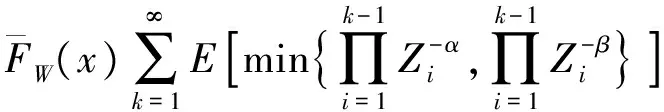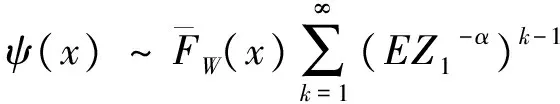带随机利率的离散时间风险模型的破产概率
2015-07-02张媛媛陈利馥王文胜
张媛媛, 陈利馥, 王文胜
(1.江苏理工学院 商学院, 江苏 常州 213001; 2.杭州师范大学 数学系, 浙江 杭州 310018)
带随机利率的离散时间风险模型的破产概率
张媛媛1, 陈利馥1, 王文胜2
(1.江苏理工学院 商学院, 江苏 常州 213001; 2.杭州师范大学 数学系, 浙江 杭州 310018)
考虑带随机利率的离散时间风险模型的破产概率. 所考虑的模型又称为期初应付年金风险模型.在该模型下,当索赔分布分别属于D∩L族、广义正则变化重尾分布族和正则变化重尾分布族时, 得到了破产概率的渐近表达式.
渐近性; 破产概率; 随机利率
0 引言
离散时间风险模型在保险业务中有着重要的应用, 例如, 汽车保险就是通过离散风险模型来刻画的.Grandell[1]和Asmussen[2]给出一些连续时间风险模型可以用离散时间风险模型来逼近.因此,研究离散时间风险模型是非常必要的.近年来出现了许多研究离散时间风险模型的文章[3-4].
更新风险模型自建立以来,许多学者都对其进行了广泛而深入的研究,为了使其更贴合实际,许多学者考虑了带利率的更新风险模型.因此,出现了许多研究带利率风险模型破产概率的文章[5-6].他们都是在连续时间风险模型下研究破产概率的.有学者研究了带利率的离散时间风险模型[7-8],他们都是考虑带常利率的.Cai[9]和 Wei[10]等人考虑了带随机利率的离散时间风险模型.Cai[9]分别利用鞅方法和更新递推方法得到了关于破产概率的随机不等式,利用这些随机不等式可以算出破产概率的上界.Wei[10]等作者得到了有限时间破产概率的递推式和最终破产概率的上界.他们都没有得到破产概率的渐近表达式.因此,本文将研究离散时间风险模型,考虑带随机利率的离散时间风险模型破产概率的渐近性.
1 模型介绍
保险公司的盈余模型由下面的递推式来描述
U0=x,Un=(Un-1+Xn)(1+In)-Yn,n=1,2,…
(1)
其中x≥0表示初始资本.{Xn,n≥1},{In,n≥1}和{Yn,n≥1}是三列独立同分布的非负随机变量序列.In表示第n个时期内(即从n-1时刻到n时刻)的利率.Xn表示第n个时期内的保费收入,并且保费是在第n个时期开始时(即n-1时刻)交.Yn表示第n个时期内的索赔额,并且索赔额是在第n个时期结束时(即n时刻)支付.记FY(x)=Pr(Y1≤x)为{Yn,n≥1}共同的分布,记FZ(x)=Pr(Z1≤x)为{Zn=1+In,n≥1}共同的分布.设{Xn,n≥1},{In,n≥1}和{Yn,n≥1}相互独立.
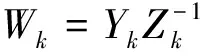
(2)
定义最终破产概率为
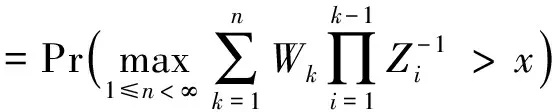
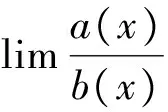
定义1 设F是定义在(-∞,∞)上的分布.若存在常数0≤α<∞,使得对任意的y>0有
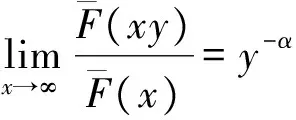
则称分布函数F具有正则变化尾.记作F∈R-α.
定义2 设F是定义在(-∞,∞)上的分布.若存在常数0≤α≤β<∞,使得对任意的y≥1有
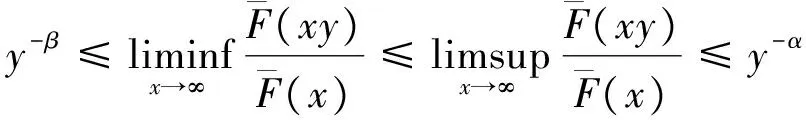
则称分布函数F具有广义正则变化尾.记作F∈ERV(-α,-β).
定义3 设F是定义在(-∞,∞)上的分布.如果对任意的0 则称分布函数F具有控制变化尾.记作F∈D. 定义4 设F是定义在(-∞,∞)上的分布.如果对任意的y有 上述重尾分布族有下面的包含关系:R⊂ERV⊂D∩L.更多有关重尾分布族的内容以及它们在金融保险中的应用可以参阅Embrechts et al[11]. 我们先来回忆一些长尾分布族的性质. 引理2 设FV1是随机变量V1的分布函数且FV1∈L.V2是一个非负随机变量.FV1V2表示V1V2的分布函数.则FV1V2∈L. 下面的引理描述了控制变化尾分布族的一个性质,可以参看Cline and Samorodnitsky[13]中的定理. 引理4 设FV1是随机变量V1的分布函数且FV1∈D.V2是一个非负随机变量.FV1V2表示V1V2的分布函数.则FV1V2∈D. 引理5 考虑前面介绍的风险模型.假设FY∈D∩L,则{Wk,k≥1}是一列独立同分布的随机变量序列且其共同的分布FW∈D∩L. 因此{Wk,k≥1}是一列同分布的随机变量序列.由引理1我们还可以得到FW∈L.由引理4知FYZ-1∈D.因此,应用引理1,对任意的0 故FW∈D.这样我们就完成了引理的证明. 下面的引理描述了重尾分布族的一些性质. 引理6[14]假设{Xk,1≤k≤m}是一列独立同分布的随机变量序列,其共同的分布为F,{θk,1≤k≤m}是另一列独立同分布的非负随机变量序列并且与{Xk,1≤k≤m}独立.另外其还满足对某一0 1) 如果F∈D∩L,那么 2) 如果F∈D∩L,那么 其中对任意的y>0, 3) 如果F∈ERV(-α,-β),其中0≤α≤β<∞,那么 4) 如果F∈R-α,其中α≥0,那么 下面的引理描述了长尾分布族的一个重要性质. 引理7[13]若分布函数F∈L,则存在函数a(·):[0,∞)→[0,∞)使得下列式子同时成立: 引理8[13]考虑前面介绍的风险模型.假设FY∈D∩L,那么 证明 由马尔可夫不等式得 定理1 考虑前面介绍的风险模型.假设FY∈D∩L,那么 证明 对任意固定的m=1,2,…,由引理1及引理5、引理6可得 (3) 用引理8证明中的类似方法我们可以得到当m充分大时,上式中的后一项和式是可以忽略掉的.因此, ψ(x) (4) (5) 利用式(3)证明中的类似方法以及引理7,我们可以得到 (6) 由引理8知,当m充分大时J2(x)是可以忽略掉的.因此,结合式(4)~式(6),我们得到了 定理2 考虑前面介绍的风险模型.假设FY∈D∩L,那么 其中对任意的y>0, 证明 对任意固定的m=1,2,…,利用定理1证明中的类似方法,我们可以得到 所以ψ(x). 另一方面,我们有 用引理8证明中的类似方法我们可以得到当m充分大时,上面的和式是可以忽略掉的.因此, 推论1 1) 如果FY∈ERV(-α,-β),其中0≤α≤β<∞,那么 2) 如果FY∈R-α,其中α≥0,那么 [1] Grandell J. Aspects of risk theory[M]. New York: Springer,1991. [2] Asmussen S. Ruin Probabilities[M]. Singapore: World Scientific, 2000. [3] Liu H, Bao Z H. On a discrete-time risk model with general income and time-dependent claims[J]. J Comput Appl Math, 2014, 260(02): 470-481. [4] Yuen K C, Li J Z, Wu R. On a discrete-time risk model with delayed claims and dividends[J]. Risk Decis Anal, 2013, 4(1): 3-16. [5] Wang D C. Finite-time ruin probability with heavy-tailed claims and constant interest rate[J]. Stoch Models,2008,24(1):41-57. [6] Li J, Wang K, Wang Y. Finite-time ruin probability with NQD dominated varying-tailed claims and NLOD inter-arrival times[J]. J System Science Comple, 2009, 22(3): 407-414. [7] Sun L, Yang H. Ruin theory in a discrete time risk model with interest income[J]. B A J, 2003, 9(3): 637-652. [8] Weng C G, Zhang Y, Tan K S. Ruin probabilities in a discrete time risk model with dependent risks of heavy tail[J]. Scand Actuarial J, 2009(3): 205-218. [9] Cai J. Discrete time risk models under rates of interest[J]. Probab Engineer Infor Sci, 2002(16): 309-324. [10] Wei X, Hu Y J. Ruin Probabilities for discrete time risk models with stochastic rates of interest[J]. Statist Probab Lett, 2008, 78(6): 707-715. [11] Embrechts P, Klüppelberg C, Mikosch T. Modelling Extremal Events for Insurance and Finance[M]. Berlin: Springer-Verlag, 1997. [12] Tang Q H. The ruin Probability of a discrete time risk model under constant interest rate with heavy tails[J]. Scand Actuarial J, 2004(3): 229-240. [13] Cline D B H, Samorodnitsky G. Subexponentiality of the product of independent random variables[J]. Stochastic Process Appl, 1994, 49(1): 75-98. [14] Tang Q H, Tsitsiashvili G. Randomly weighted sums of subexponential random variables with application to ruin the-ory[J]. Extremes, 2003, 6(3): 171-188. [责任编辑:李春红] Ruin Probability of a Discrete Time Risk Modelunder Stochastic Rates of Interest ZHANG Yuan-yuan1, CHEN Li-fu1, WANG Wen-sheng2 (1.School of Business, Jiangsu University of Technology, Changzhou Jiangsu 213001, China)(2.Department of Mathematics, Hangzhou Normal University, Hangzhou Zhejiang 310018, China) The ruin probability of a discrete time risk model under stochastic interest rate was considered in this paper.The risk model is also called the annuity-due risk model. When the common distribution of claim sizes belongs to the classD∩L, ERVandR, respectively,an asymptotic formula for the ultimate ruin probability is derived. asymptotic; ruin probability; stochastic interest rate 2015-06-07 浙江省自然科学基金资助项目(LY14A010025) 张媛媛(1985-),女,江苏扬州人,讲师,博士,主要从事风险理论方面的研究. E-mail: zyylhh1227@163.com O211.6 A 1671-6876(2015)04-0283-05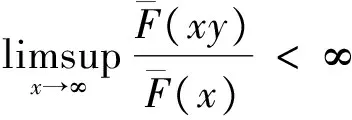
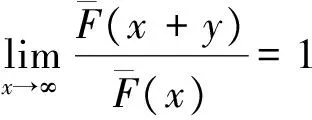
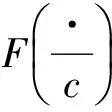
2 破产概率的渐近表达式