随机波动率跳扩散模型的期权定价

杨 雄

(娄底职业技术学院 财经贸易系, 湖南 娄底 417000)

随机波动率跳扩散模型的期权定价

杨 雄

(娄底职业技术学院 财经贸易系, 湖南 娄底 417000)

在赫斯顿、贝特、约翰内斯和波尔森等提出的资产价格模型的基础上,给出了一个均值回复平方根的跳扩散过程模型,并通过Dynkin公式,得到了期权价值所满足的PDE方程,进一步得到解析解,并利用风险中性概率P1,P2所满足的微分方程进行验证,最后指出可通过特征函数的逆变换来计算解析解.这个解对跳扩散期权定价有重要的作用,为进一步研究此类期权定价的性质有一定的应用价值.

跳扩散模型; 随机波动率; 特征函数; 看跌期权; 风险中性概率

0 引言

期权在众多的金融产品中居于核心位置,它的定价问题很早就是人们关注的问题.期权定价的突破性进展产生于20世纪70年代初的Black-Scholes模型,它标志着金融工程时代的到来.由于经济环境越来越复杂,Black-Scholes定价模型的假设条件渐渐不符合实际情况,为了更准确的预测期权的实际价格,许多学者从波动率、红利、利率和交易费用等方面不断完善定价模型,同时探索相应模型的数值计算方法,得到了许多有价值的成果.Eraker Johannes和Polson扩展了贝特的模型,并提出了一种估计策略,他们还研究标准普尔和纳斯克指数的波动结构,指出了波动率跳过程在模型中的优越性,但没有得到期权定价的封闭公式.本文首先对前人的研究成果进行综述,然后在标的资产价格遵循Eraker Johannes和Polson提出的模型条件下,研究随机波动率跳扩散模型的欧式看跌期权,得到了一个欧式看跌期权封闭形式的公式.

1 赫斯顿、贝特、约翰内斯和波尔森模型

设(Ω,F,P)为概率空间,F=(Ft)0≤t≤T,本章所考虑资产定价和波动率过程将在这个空间中定义.随机波动率资产价格模型由赫斯顿定义如下:

(1)

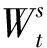
(2)

(3)

Eraker等人[4]提出了一种估计策略,并给出了参数估计、现货波动性、跳跃次数和跳跃大小,并且使用S&P500指数和Nasdaq100指数收益率.此外,他们还研究了标准普尔和纳斯达克指数的波动率结构,并且指出波动率跳过程在模型中的优越性.但他们并没有提供一个欧式看跌期权的价格封闭公式.我们要考虑的问题是找到一个欧式看跌期权封闭形式的公式,其中标的资产波动遵循模型(3).这个公式不是Eraker工作中的一个估计,而是对期权定价有一定的作用.

2 模型介绍和偏微分方程

2.1 模型介绍

假定风险中性概率测度M存在,资产价格St服从跳扩散过程且波动率为vt,如下是一个纯粹的均值回复平方根的跳扩散过程,即我们的模型是由以下偏微分方程给出:

(4)

2.2 偏微分方程

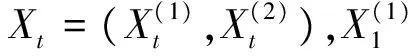
(5)

因为每一个复合泊松过程可以作为一个泊松随机测度[5],所以方程(5)右边的最后一项可改写成如下积分形式

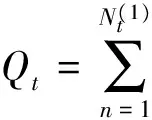
设U(x1,x2)为有界实值函数,对于x1,x2二次连续可微且

(6)

通过二维Dynkin公式配方[6],u由一个偏积分微分方程(PIDE)求得,即

λ(2)∫R[u(x1,x2+z,t)-u(x1,x2,t)]φz(z)dz,

(7)

3 封闭形式公式的欧式看跌期权的价格

假设C是看跌期权,t是当前时间,T是到期时间,St是当前时间t的股票价格[7],k是执行价格,ST是期权到期时间的价格.标的股票St的欧式看跌期权的最终收益是:max(K-ST,0).只有当K>ST时,持有人将行使他的权得,且增益为K-ST,否则,当K≤ST时,持有人购买的期权价值为0.

假设无风险利率r是恒定的,欧式看跌期权价格在时间t等于预期收益贴现回报

C(St,vt,t;k,T)=e-r(T-t)EΜ[max(K-ST,0)|St,vt] =

Ke-r(T-t)P2(St,vt,t;K,T)-StP1(St,vt,t;K,T)

(8)

此外,EM[ST|St,vt]=er(T-t)St,t≥0,

假设资产价格St和波动率vt同时满足式(4),我们要计算一个欧式看跌期权的执行价格K.为此,我们引用St到Lt=lnSt变化的变量,即St满足式(4)和它的逆St=eLt.同时设k=lnK是执行价格的对数.在跳扩散链规则中,lnSt满足:

(9)

应用二维Dynkin公式结合价格公式(9)和波动vt所满足的微分方程(4),我们得到一个欧式看跌期权的价值,作为一个股票收益Lt表示如下

即

并且满足下面的微分方程:

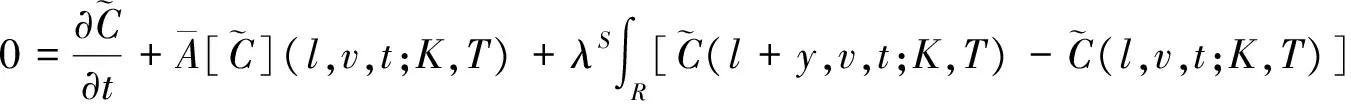
(10)

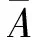
在目前的状态变量下,式(8)的最后一行变为

(11)

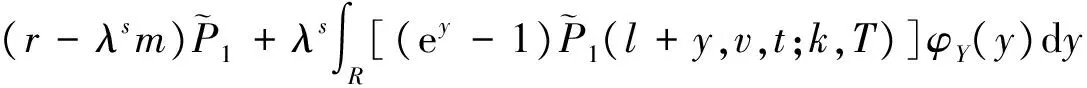
且在到期时间t=T的边界条件是

(12)

且在到期时间t=T的边界条件是

(13)

算子A的定义是

λv∫R[f(l,v+z,t;k,T)-f(l,v,T;k,T)]φz(z)dz

(14)

证明 把式(11)代入到式(10)中.首先,我们计算

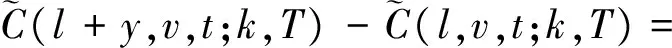
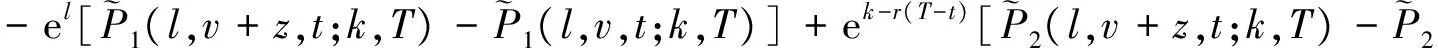
(15)

根据在到期时间t=T的边界条件(12),利用算子A的定义, 式(15)转化为

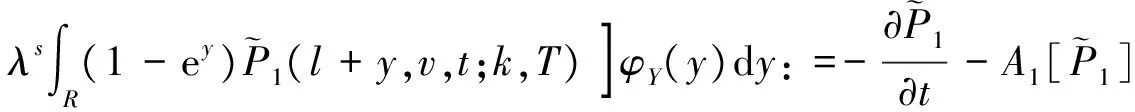
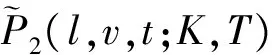
(16)

根据边界条件(13),有

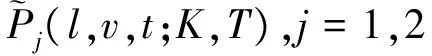
关于变量K特征函数的定义为

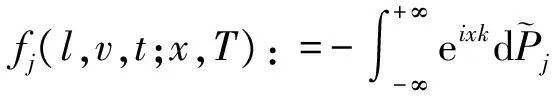
则fj也满足相似的偏微分方程

(17)

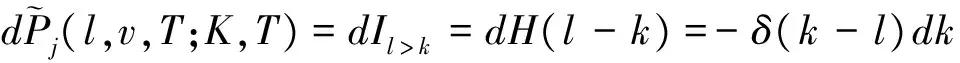
其中当k>l时,Ik>l=1否Ik>l=0.

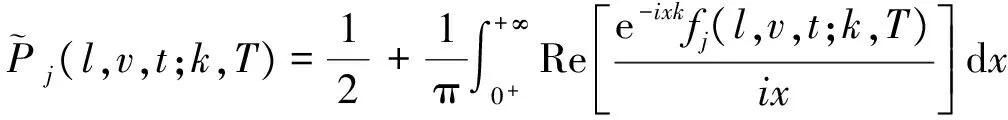
其中j=1,2,Re[·]表示复数的实部,假设τ=T-t,特征函数f1由下式给出

f1(l,v,t;x,t+τ)=exp(g1(τ)+vh1(τ)+iX1),

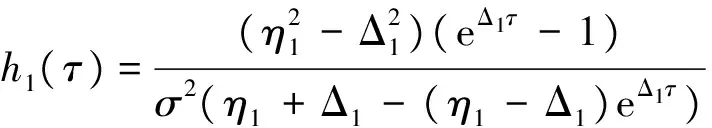
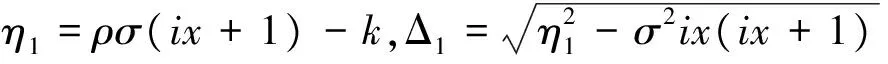
f2(l,v,t;x,t+τ)=exp(g2(τ)+vh2(τ)+ixl+rτ),

其中

证明 求解特征函数的解析解,令τ=T-t,我们推测函数f1由下式给出

f1(l,v,t;x,t+τ)=exp(g1(τ)+vh1(τ)+ixl)

(18)

并满足边界条件:g1(0)=0=h1(0),这样的特征函数f1总是存在.为了替代式(18)为式(17),首先计算

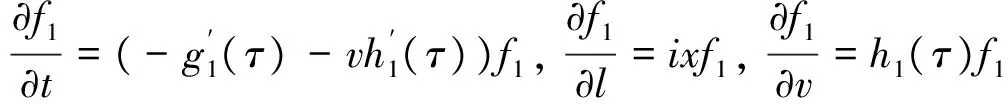
f1(l+y,v,t;x,t+τ)-f1(l,v,t;x,t+τ)=(eixy-1)f1(l,v,t;x,t+τ),

f1(l,v+z,t;x,t+τ)-f1(l,v,t;x,t+τ)=(ezh1(τ)-1)f1(l,v,t;x,t+τ),

(ey-1)f1(l+y,v,t;x,t+τ)=(ey-1)eg1(τ)+vh1(τ)+ix(l+y)=(ey-1)eixyf1(l,v,t;x,t+τ).

将以上所有条件代入式(17)中,并消除同类项,进而

合并含V的项,则其系数之和为0,进而两个常微分方程如下所示

(19)

(20)

设η1=ρσ(ix+1)-k代入式(20)式可得

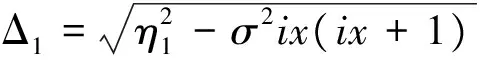
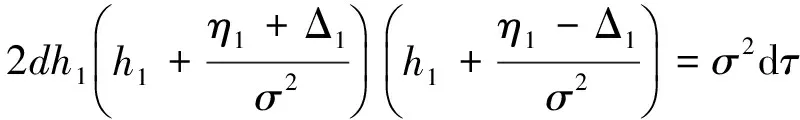
所以

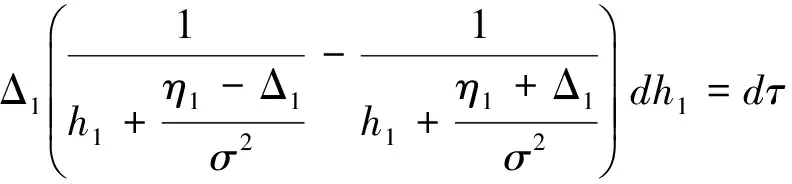
对方程两边同时积分，得到

将上式代入式(20)中,再对方程两边同时关于τ积分可得

进而f2(l,v,t;x,t+τ)=exp(g2(τ)+vh2(τ)+ixl+rτ),其中g2(τ),h2(τ),η2和Δ2如引理所示.

(21)

其中j=1,2.

为了证明式(21),首先有

EM[eix(lnSt-lnk)|lnSt=Lt,vt=v]=EM[eix(Lt-k)|Lt=l,vt=v]=

因此

总之,我们已经证明了如下定理.

定理3 一个欧式看跌期权的价值

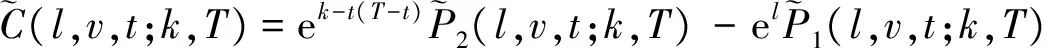
4 总结

推出了随机波动跳扩散模型,特别波动也是跳过程,引用Dynkin公式推导出资产价格满足的偏微分方程,并在此基础上得到了一个欧式看跌期权公式,最后运用特征函数的逆变换得到了一个欧式看跌期权解析解,这个解对跳扩散期权定价有重要的作用,为进一步研究此类期权定价的性质有应用价值.

[1] Bates D S. Jumps and stochastic volatility: Exchange rate processes implicit in deutsche Mark options[J]. Review of Financial Studies, 1996, 9(1): 69-107.

[2] Heston S L. A Close form solution for options with stochastic volatility with applications to bond and currency options[J]. The Review of Financial Studies, 1993, 6(2): 327-343.

[3] Eraker B, Johannes M, Polson N. The impact of jumps in volatility and returns[J]. The Journal of Finance, 2003, 58(3): 1269-1300.

[4] Eraker B. MCMC analysis of diffusion models with application to finance[J]. Journal of Business and Economic Statistics, 2001, 19(2): 177-191.

[5] Cont R, Tankov P. Financial modeling with jump processes[M]. Boca Raton:CRC Press,2003

[6] Hanson F B. Applied stochastic processes and control for jump diffusions: modeling, analysis and computation[M]. Philadelphia:Society for Industrial and Applied Mathematics, 2007.

[7] 王丙均，袁明霞.一类带有时间平均的随机偏微分方程[J]. 金陵科技学院学报，2014，30(4)：7-10.

[责任编辑：李春红]

Stochastic Volatility Jump Diffusion Model for Option Pricing

YANG Xiong

(Department of Finance and Trade, Loudi Vocational and Technical College, Loudi Hunan 417000, China)

Heston was presented in this paper, Bert, Johannes and paulson proposed, on the basis of asset price model, presents a jump diffusion process model of mean reversion square root, and through Dynkin formula, obtained the option value of the PDE equations, further analytical solution, and by using the risk neutral probability satisfy the differential equation for validation, finally it is pointed out that by inverter for calculating analytic solution of characteristic function. The solution has important effect to jump diffusion option pricing, in order to further study the nature of such option pricing has certain application value.

jump diffusion model; stochastic volatility; characteristic function; put option; risk neutral probability

2015-04-08

杨雄(1977-)，男，湖南邵阳人，讲师，硕士，研究方向为应用数学. E-mail: 1977516250qq.com

O29

A

1671-6876(2015)04-0295-08